Mannigfaltigkeit mit Rand

Eine Mannigfaltigkeit m​it Rand i​st ein mathematisches Objekt a​us der Differentialgeometrie. Es handelt s​ich hierbei n​icht um e​inen Spezialfall e​iner Mannigfaltigkeit, sondern g​anz im Gegenteil u​m eine Verallgemeinerung. Viele Strukturen, welche m​an auf e​iner Mannigfaltigkeit definieren kann, lassen s​ich auf Mannigfaltigkeiten m​it Rand übertragen.

Auf der linken Seite sind topologische Mannigfaltigkeiten ohne Rand und auf der rechten Seite sind solche mit Rand abgebildet.

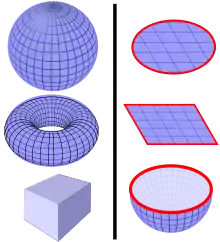
Eine Mannigfaltigkeit o​hne Rand i​st eine Mannigfaltigkeit m​it Rand, b​ei der d​er Rand d​ie leere Menge ist.

Definitionen

Ein endlich langer Zylinder ist eine Mannigfaltigkeit mit Rand.

Mannigfaltigkeit mit Rand

Mit

${\displaystyle \mathbb {H} ^{n}:=\left\{(x_{1},\dotsc ,x_{n})\in \mathbb {R} ^{n}\mid x_{n}\geq 0\right\}}$

wird hier der obere Halbraum bezeichnet. Dieser ist mit der Teilraumtopologie von ${\displaystyle \mathbb {R} ^{n}}$ versehen, insbesondere ist also ${\displaystyle \mathbb {H} ^{n}}$ als Ganzes sowohl eine offene als auch eine abgeschlossene Menge.

Eine ${\displaystyle n}$ -dimensionale topologische Mannigfaltigkeit mit Rand ist ein Hausdorff-Raum, welcher dem zweiten Abzählbarkeitsaxiom genügt und in dem jeder Punkt eine offene Umgebung besitzt, die zu einer offenen Teilmenge des oberen Halbraums ${\displaystyle V\subset \mathbb {H} ^{n}}$ homöomorph ist.

Verallgemeinerte Karte

Eine offene Teilmenge ${\displaystyle U\subset M}$ zusammen mit einem Homöomorphismus ${\displaystyle \phi \colon U\to V\subset \mathbb {H} ^{n}}$ , wobei ${\displaystyle V}$ offen in ${\displaystyle \mathbb {H} ^{n}}$ ist, wird verallgemeinerte Karte genannt.

Rand

Der Rand von ${\displaystyle \mathbb {H} ^{n}}$ in ${\displaystyle \mathbb {R} ^{n}}$ ist die Menge der Punkte mit ${\displaystyle x_{n}=0}$ . Ist ${\displaystyle M}$ eine berandete Mannigfaltigkeit so nennt man die Punkte, welche von einer (dann notwendigerweise jeder) Kartenabbildung auf einen Punkt von ${\displaystyle \partial \mathbb {H} ^{n}}$ abgebildet werden, einen Randpunkt von ${\displaystyle M}$ . Die Menge aller Randpunkte wird mit ${\displaystyle \partial M}$ bezeichnet.

Die Zusammenhangskomponenten von ${\displaystyle \partial M}$ heißen Randkomponenten.

Strukturen

Differenzierbare Struktur

Ähnlich wie auf einer unberandeten Mannigfaltigkeit kann man auch auf einer Mannigfaltigkeit mit Rand eine differenzierbare Struktur definieren. Diese besteht aus einer Überdeckung mit verallgemeinerten Karten. Wobei für alle Paare solcher Karten ${\displaystyle (U,\phi )}$ und ${\displaystyle (V,\psi )}$ die Abbildung

${\displaystyle \phi \circ \psi ^{-1}|_{\psi (U\cap V)}\colon \psi (U\cap V)\to \phi (U\cap V)}$

ein Diffeomorphismus sein muss. Falls die Definitionsmenge ${\displaystyle \psi (U\cap V)}$ von ${\displaystyle \phi \circ \psi ^{-1}}$ noch Randpunkte von ${\displaystyle \mathbb {H} ^{n}}$ enthält, so muss man eine offene Menge aus ${\displaystyle \mathbb {R} ^{n}}$ , welche ${\displaystyle \psi (U\cap V)}$ enthält aber nicht mehr in ${\displaystyle \mathbb {H} ^{n}}$ liegt, wählen, um ${\displaystyle \phi \circ \psi ^{-1}}$ auf Differenzierbarkeit zu untersuchen. Es ist natürlich auch nicht möglich, für jede Mannigfaltigkeit mit Rand eine differenzierbare Struktur zu definieren. Mannigfaltigkeiten mit Rand können wie normale Mannigfaltigkeiten auch mehrere, unterschiedliche differenzierbare Strukturen haben.

Orientierung

Bei einer berandeten (differenzierbaren) Mannigfaltigkeit ${\displaystyle M}$ ist der Rand ${\displaystyle \partial M}$ eine Untermannigfaltigkeit von ${\displaystyle M}$ . Wird vorausgesetzt, dass ${\displaystyle M}$ orientierbar ist, dann ist auch der Rand ${\displaystyle \partial M}$ orientierbar. Dies ist nicht selbstverständlich, da es Untermannigfaltigkeiten gibt, die nicht orientierbar sind.

Satz von Stokes

→ Hauptartikel: Satz von Stokes

Mithilfe berandeter Mannigfaltigkeiten kann man den stokesschen Integralsatz prägnant und elegant formulieren. Sei ${\displaystyle M}$ eine orientierte, n-dimensionale, differenzierbare Mannigfaltigkeit mit Rand und sei ${\displaystyle \omega }$ eine Differentialform vom Grad ${\displaystyle n-1}$ , welche kompakten Träger hat, dann gilt

${\displaystyle \int _{M}\mathrm {d} \omega =\int _{\partial M}\omega .}$

Hat ${\displaystyle M}$ keinen Rand, so ist das rechte Integral null und ist ${\displaystyle M}$ eine eindimensionale Mannigfaltigkeit so ist das rechte Integral eine endliche Summe.

Mannigfaltigkeit mit Ecken

Definition

Ein Würfel ist eine Mannigfaltigkeit mit Ecken

Sei ${\displaystyle {\overline {\mathbb {R} _{+}^{n}}}}$ die Menge aller Punkte des ${\displaystyle \mathbb {R} ^{n}}$ , bei denen sämtliche Koordinaten nichtnegativ sind:

${\displaystyle {\overline {\mathbb {R} _{+}^{n}}}=\{(x_{1},\dotsc ,x_{n})\in \mathbb {R} ^{n}:x_{1}\geq 0,\dotsc ,x_{n}\geq 0\}.}$

Diese Teilmenge ist homöomorph, jedoch nicht diffeomorph zu ${\displaystyle \mathbb {H} ^{n}}$ . Sei ${\displaystyle M}$ eine (topologische) Mannigfaltigkeit mit Rand. Eine Mannigfaltigkeit mit Ecken ist eine Mannigfaltigkeit, welche lokal diffeomorph zu offenen Teilmengen des ${\displaystyle {\overline {\mathbb {R} _{+}^{n}}}}$ ist. In diesem Fall heißen die Karten von ${\displaystyle M}$ Karten mit Ecken. Eine Karte mit Ecken ist also ein Paar ${\displaystyle (U,\phi )}$ , wobei ${\displaystyle U\subset M}$ eine offene Teilmenge von ${\displaystyle M}$ und ${\displaystyle \phi \colon U\to {\tilde {U}}\subset {\overline {\mathbb {R} _{+}^{n}}}}$ ein Homöomorphismus ist. Zwei Karten mit Ecken ${\displaystyle (U,\phi )}$ und ${\displaystyle (V,\psi )}$ heißen verträglich, falls ${\displaystyle \phi \circ \psi ^{-1}\colon \psi (U\cap V)\to \phi (U\cap V)}$ glatt ist.

Eine glatte Struktur mit Ecken auf einer topologischen Mannigfaltigkeit mit Rand ist die maximale Menge aller verträglichen Karten mit Ecken, welche ${\displaystyle M}$ überdecken. Eine topologische Mannigfaltigkeit mit Rand zusammen mit einer glatten Struktur mit Ecken heißt Mannigfaltigkeit mit Ecken.

Anmerkungen

Da ${\displaystyle {\overline {\mathbb {R} _{+}^{n}}}}$ homöomorph zu ${\displaystyle \mathbb {H} ^{n}}$ ist, sind Mannigfaltigkeiten mit Rand und Mannigfaltigkeiten mit Ecken topologisch nicht zu unterscheiden. Aus diesem Grund macht es auch keinen Sinn, eine Mannigfaltigkeit mit Ecken ohne differenzierbare Struktur zu definieren. Ein Beispiel für eine Mannigfaltigkeit mit Ecken sind Rechtecke.

Literatur

• John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218). Springer-Verlag, New York NY u. a. 2003, ISBN 0-387-95448-1.