Theoretische Biologie

Die theoretische Biologie entwickelt formale Modelle zur Beschreibung biologischer Phänomene. Dazu nutzt sie insbesondere Methoden aus der Mathematik. Es werden Modelle und Theorien erarbeitet, um die Struktur und Dynamik lebender Systeme zu beschreiben. Viele fundamentale Erkenntnisse der Biologie, etwa die Beschreibung evolutionär stabiler Strategien oder auch die Replikatorgleichungen, stammen aus der theoretischen Biologie. In ihrer rein mathematischen Ausrichtung wird die theoretische Biologie auch Biomathematik genannt und ist ein Teilgebiet der Angewandten Mathematik.

Phasenraumtrajektorien eines Räuber-Beute-Systems. Einer der ersten mathematischen Gegenstände der Theoretischen Biologie.

Geschichte

1920 Frühes Standardwerk der vormathematischen theoretischen Biologie

Die Idee einer theoretischen Biologie entwickelte sich um 1900. An zentraler Stelle taucht der Begriff theoretische Biologie erstmals 1901 im Titel des Buches Einleitung in die theoretische Biologie von Johannes Reinke auf. In der sich hieraus entwickelnden Tradition wurde die Aufgabe der theoretischen Biologie allerdings noch weniger in der Mathematisierung der biologischen Theorien, sondern vielmehr als konzeptionelle Grundlegung für die Biologie gesehen. Die Biologie war zu diesem Zeitpunkt als Disziplin gerade erst dabei, sich zu formieren und der Theoriebestand der vielen verschiedenen Einzeldisziplinen war unübersichtlich und in großen Teilen widersprüchlich. Im 19. Jahrhundert hatte man noch gehofft, dass die Evolutionstheorie Darwins die Aufgabe einer Grundlegung für die Biologie übernehmen könnte. Aber der Darwinismus durchlief um 1900 eine tiefe Krise.

Im Anschluss an Reinke erschienen zahlreiche Publikationen von Autoren, die sich mit theoretischen und philosophischen Problemen der Biologie auseinandersetzen. Als zentral für diese frühe Phase der theoretischen Biologie sind vor allem Jakob Johann von Uexküll und Julius Schaxel zu nennen. Beide arbeiteten mit dem Begriff theoretische Biologie. Während Uexküll eine eigene Neukonzeption für die Biologie erarbeiten wollte, versuchte Schaxel mit seinem Buch Grundzüge der Theoriebildung in der Biologie von 1919 und der im gleichen Jahr gegründeten Schriftenreihe Abhandlungen zur theoretischen Biologie auf die theoretischen Probleme der Biologie aufmerksam zu machen und ein Forum für die Bearbeitung dieser Probleme zu etablieren. Weitere wichtige Vertreter der theoretischen Biologie waren Max Hartmann und Ludwig von Bertalanffy.

Die heutige Bedeutung des Begriffs theoretische Biologie als einer Biologie mit mathematischen Mitteln entwickelte sich erst relativ spät: Frühe Protagonisten der mathematisch verstandenen theoretischen Biologie waren um 1925/26 der Mathematiker Alfred J. Lotka sowie der Physiker Vito Volterra, die zu dieser Zeit unabhängig voneinander Systeme von gewöhnlichen Differentialgleichungen zur Beschreibung der Dynamik von Populationen angaben. Doch erst während und nach dem Zweiten Weltkrieg entwickelte sich eine breite mathematikorientierte Tradition in der theoretischen Biologie. Hier spielte auch der Einfluss von Biologen aus Russland eine große Rolle, wo die Verbindung von Mathematik und Biologie eine längere Tradition und eine stärkere Verbreitung hatte. Vor allem die Populationsgenetik war hier ein wichtiger Bereich. Biologen wie Theodosius Dobzhansky, Ronald Fisher, Sewall Wright und John Burdon Sanderson Haldane, die auch zu den zentralen Figuren der synthetischen Evolutionstheorie gehörten, leisteten hier wichtige Pionierarbeit. 1948 folgte die Einrichtung des weltweit ersten Graduiertenstudiengangs in Mathematischer Biologie durch Nicolas Rashevsky. Von 1952 bis 1954 legte Alan Turing mit epochemachenden Ergebnissen zur Musterbildung in biologischen Systemen, insbesondere dem nach ihm benannten Turing-Mechanismus, die Grundlage für die Mathematisierung der Entwicklungsbiologie.

Heutzutage erlebt aber auch das ursprüngliche Programm der Theoretischen Biologie als Philosophie der Biologie neuen Aufschwung.

Bereiche

Weite Teilgebiete der theoretischen Biologie bedienen sich mathematischer Methoden aus dem Gebiet der Dynamischen Systeme zur Modellierung biologischer Zusammenhänge. Eine gewisse Verwandtschaft besteht in Teilen der theoretischen Biologie mit Themengebieten der theoretischen Informatik und Bioinformatik. In diesen letzteren Bereichen kommen vor allem Werkzeuge aus der Diskreten Mathematik zur Verwendung.

Unter den Bereichen der theoretischen Biologie befinden sich unter anderem:

Theoretische Ökologie

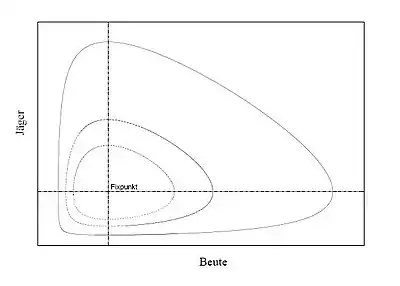
Hier wird unter anderem versucht, Aussagen über die Dynamik von Populationen und Biozönosen zu machen. Als grundlegend erweisen sich die in fast jeder ökologischen Interaktionstruktur gegenwärtigen Räuber-Beute-Beziehungen. Bei der mathematischen Formulierung von Räuber-Beute-Modellen, die erstmals in den 1920er-Jahren von Lotka und Volterra unternommen wurde, kommen klassischer Weise vor allem gewöhnliche Differentialgleichungen (z. B. die Lotka-Volterra-Gleichungen) und Differenzengleichungen zur Anwendung. Eine Schwierigkeit besteht in der Tatsache, dass viele biologische Zusammenhänge in natürlicher Weise auf nichtlineare Gleichungen führen, die nur über numerische, indirekte oder qualitative Methoden untersucht werden können.

Ein stärker anwendungsbezogener Unterbereich der theoretischen Ökologie macht sich die Möglichkeiten expliziter Computersimulation zunutze und geht von einfachen multiagentbasierten Simulationen bis zur computergestützten Darstellung ganzer Ökosysteme. Hier besteht ein fließender Übergang zwischen theoretischer Ökologie und praktischem Ökosystemmanagement.

Mathematische Epidemiologie

Fragen nach der Form und Geschwindigkeit der Ausbreitung von ansteckenden Krankheiten, sowie zur Wirksamkeit von Schutzmaßnahmen, versucht die mathematische Epidemiologie exakt zu fassen und auf Grundlage der Theorie dynamischer Systeme zu beantworten. Beispielsweise kann das sogenannte SIR-Modell dazu eingesetzt werden, die Epidemiologie von Influenza zu beschreiben. Die verwendeten Gleichungen sind oft den Gleichungen der theoretischen Ökologie nah verwandt.

Theoretische Neurobiologie

Gearbeitet wird, wie auch in der experimentellen Neurobiologie, auf verschiedenen Integrationsebenen. Die Aufgaben der theoretischen Neurobiologie, auch Computational Neuroscience genannt, erstrecken sich damit beispielsweise von der Modellierung eines oder einiger weniger Ionenkanäle bis hin zur Analyse und Simulation großer neuronaler Verbände. Ein Beispiel ist die Modellierung von bestimmten Hirnfunktionen, zum Beispiel die Generierung des Tag-Nacht-Zyklus (Circadiane Rhythmik). Es bestehen teils enge Verbindungen zur Neuroinformatik.

Theoretische Evolutionsbiologie

Die theoretische Evolutionsbiologie untersucht mit mathematischen Methoden die Dynamik von evolvierenden Systemen. Die klassische theoretische Evolutionsbiologie basiert zu großen Teilen auf einflussreichen Arbeiten von Fischer, Wright und Haldane. Ein jüngeres Teilgebiet der theoretischen Evolutionsbiologie ist die Evolutionäre Spieltheorie zu der unter anderen John Maynard Smith[1] wichtige Grundlagen schuf. Im Mittelpunkt des Interesses stehen dort als gemeinsames Abstraktum selbstreplizierender Systeme die sogenannten Replikatordynamiken und evolutionär stabile Strategien. Die Grundgleichungen der Replikatordynamik sind teilweise über Diffeomorphismen mit Lotka-Volterra-Systemen verwandt, wie Arbeiten von Hofbauer zeigen. In neuerer Zeit findet eine stärkere Beschäftigung mit endlichen Populationen statt. In endlichen Populationen spielen stochastische Effekte eine größere Rolle. Das Konzept der evolutionär stabilen Strategie wurde von Martin A. Nowak auf den Fall endlicher Populationen ausgeweitet.

Weitere mathematisch orientierte Felder der theoretischen Biologie

Künstliches Leben
Metabolic Control Analysis
Theoretische Entwicklungsbiologie
Theoretische Immunologie

Entwicklung

In jüngerer Zeit ist die im anglo-amerikanischen Kulturraum seit längerem stark expandierende theoretische Biologie auch in Deutschland im Aufstieg begriffen. Davon zeugt die Einrichtung mehrerer Lehrstühle für Theoretische Biologie; es kann eine Diversifikation der Forschungsthemen beobachtet werden. Ein Zentrum der theoretischen Biologie in Deutschland stellt das Institut für Theoretische Biologie an der Humboldt-Universität zu Berlin dar. Historisch wurden gelegentlich auch einige nicht mathematische Bereiche der Biologie zur Theoretischen Biologie gezählt.

Studium

Als reguläres Fach des Grundstudiums bzw. der Bachelorausbildung ist theoretische Biologie nicht an allen Hochschulen verpflichtend.

Als Hauptfach im Studium der Biologie kann theoretische Biologie derzeit unter anderem an der Humboldt-Universität in Berlin und der Universität Bonn studiert werden. Obwohl Art und Umfang der Mathematikausbildung von Biologiestudenten mancherorts stark gesteigert wurden, verfügt nach wie vor nur ein geringer Teil der Biologen über Kenntnisse, die zur Forschung in der theoretischen Biologie befähigen.

An mehreren Universitäten besteht die Möglichkeit, theoretische Biologie im Rahmen eines Mathematikstudiums mit Schwerpunkt in der Angewandten Mathematik zu studieren. Die Universität Greifswald bietet, Stand 2018, den grundständigen Studiengang „Biomathematik“, Bachelor of Science und Master of Science, („B.Sc.“ und „M.Sc“)[2] an. Daneben bieten unter anderem die Universitäten Wien und Oxford eine Spezialisierung im Bereich der theoretischen Biologie an. Wien bietet ein Masterstudium. Schwerpunkt des Departments sind quantitative Verfahren in der Entwicklungsbiologie mit Hilfe hochauflösender micro-CT-Bildgebung, sowie Modellierung und theoretische Integration von Entwicklungsprozessen.[3]

Während und nach der Promotion kann das Studium an mittlerweile zahlreichen auf theoretische Biologie spezialisierten Forschungsinstituten fortgesetzt werden.

Literatur

J. T. Bonner: The Evolution of Complexity by Means of Natural Selection. Princeton University Press, Princeton 1988.
J. Bammert, H. J. Jesdinsky, E. Walter, C. Otto, R. Roßner: Biomathematik für Mediziner. 3. Auflage. Teubner, 1988.
Nicholas F. Britton: Essential Mathematical Biology. Springer.
H. Hertel: Structure, Form, Movement. Reinhold Publishing Corp, New York 1963.
M. Mangel: Special Issue, Classics of Theoretical Biology. (part 1). In: Bull. Math. Biol. Band 52, Nr. 1/2, 1990, S. 1–318.
J. Murray: Mathematical Biology. Springer.
P. Prusinkiewicz, A. Lindenmeyer: The Algorithmic Beauty of Plants. Springer-Verlag, Berlin 1990.
D. W. Thompson: On Growth and Form. 2. Auflage. Cambridge University Press., Cambridge 1942. (2 Bände)
S. Vogel: Life's Devices: The Physical World of Animals and Plants. Princeton University Press, Princeton 1988.
Ricard Solé, Brian Goodwin: Signs of Life: How Complexity Pervades Biology. Basic Books, 2001, ISBN 0-465-01927-7.
How the Leopard Changed its Spots: The Evolution of Complexity. Scribner, 1994, ISBN 0-02-544710-6. (deutsch: Der Leopard, der seine Flecken verliert. Piper, München 1997, ISBN 3-492-03873-5)
Gerry Webster, B. C. Goodwin: Form and Transformation: Generative and Relational Principles in Biology. Cambridge Univ. Press, 1996, ISBN 0-521-35451-X.
Kwang W. Jeon, Richard J. Gordon (Hrsg.): Mechanical Engineering of the Cytoskeleton in Developmental Biology (International Review of Cytology). Academic Press, London 1994, ISBN 0-12-364553-0.
Brian Goodwin, Peter Saunders u. a. (Hrsg.): Theoretical Biology: Epigenetic and Evolutionary Order for Complex Systems. Edinburgh University Press, 1989, ISBN 0-85224-600-5.
A. J. Lotka: Elements of Physical Biology. Williams and Wilkins, Baltimore 1925, ISBN 0-486-60346-6.
A. J. Lotka: Analytical Theory of Biological Populations. (= The Plenum Series on Demographic Methods and Population Analysis). Plenum Press, New York 1998, ISBN 0-306-45927-2.

Weblinks

Was ist theoretische Biologie?
F. Hoppensteadt: Getting Started in Mathematical Biology. (PDF; 197 kB). Notices of American Mathematical Society, Sept. 1995.
M. C. Reed: Why Is Mathematical Biology So Hard? (PDF; 52 kB). Notices of American Mathematical Society, März 2004.
R. M. May: Uses and Abuses of Mathematics in Biology. (PDF; 222 kB). In: Science. 6. Februar 2004.
J. D. Murray: How the leopard gets its spots? (MS Word; 931 kB). In: Scientific American. Band 258, Nr. 3, 1988, S. 80–87.
S. Schnell, R. Grima, P. K. Maini: Multiscale Modeling in Biology. In: American Scientist. Vol 95, März–April 2007, S. 134–142.

Fachjournale

Forschungseinrichtungen

Fachgesellschaften

American Mathematical Society
British Society of Developmental Biology
European Mathematical Society
ESMTB: European Society for Mathematical and Theoretical Biology
The International Biometric Society, abgerufen am 23. Dezember 2018.
International Society for Ecological Modelling
London Mathematical Society
Société Francophone de Biologie Théorique, abgerufen am 23. Dezember 2018.
Society for Industrial and Applied Mathematics
Society for Mathematical Biology

Einzelnachweise

J. Maynard Smith: Evolution and the Theory of Games. Cambridge University Press, 1982.
Universität Greifswald - Alle Studienfächer in alphabetischer Reihenfolge (pdf; 77,5 kB; 3 Seiten), Stand: 15. Juni 2018, S. 1, abgerufen am 28. Oktober 2018.
Department für Theoretische Biologie Universität Wien

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] J. Maynard Smith: Evolution and the Theory of Games. Cambridge University Press, 1982.

[UniGreifswald_Studienfächer-2] Universität Greifswald - Alle Studienfächer in alphabetischer Reihenfolge (pdf; 77,5 kB; 3 Seiten), Stand: 15. Juni 2018, S. 1, abgerufen am 28. Oktober 2018.

[3] Department für Theoretische Biologie Universität Wien