Künstliches neuronales Netz

Künstliche neuronale Netze, auch künstliche neuronale Netzwerke, kurz: KNN (englisch artificial neural network, ANN), sind Netze aus künstlichen Neuronen. Sie sind Forschungsgegenstand der Neuroinformatik und stellen einen Zweig der künstlichen Intelligenz dar.

Vereinfachte Darstellung eines künstlichen neuronalen Netzes

Schema für ein künstliches Neuron

Künstliche neuronale Netze haben, ebenso wie künstliche Neuronen, ein biologisches Vorbild. Man stellt sie natürlichen neuronalen Netzen gegenüber, die eine Vernetzung von Neuronen im Nervensystem eines Lebewesens darstellen. Bei KNNs geht es allerdings mehr um eine Abstraktion (Modellbildung) von Informationsverarbeitung, weniger um das Nachbilden biologischer neuronaler Netze und Neuronen, was eher Gegenstand der Computational Neuroscience ist. Es ist jedoch zu beobachten, dass die Grenzen zwischen diesen Teildisziplinen zunehmend verschwinden, was auf die nach wie vor große Dynamik und Interdisziplinarität dieses Forschungszweigs zurückzuführen ist. Aus der Biologie motiviert ist die Modellierung mittlerweile so gut, dass viele Aufgabenstellungen wesentlich besser als vom Menschen erledigt werden.

Beschreibung

Künstliche neuronale Netze basieren meist auf der Vernetzung vieler McCulloch-Pitts-Neuronen oder leichter Abwandlungen davon. Grundsätzlich können auch andere künstliche Neuronen Anwendung in KNNen finden, z. B. das High-Order-Neuron. Die Topologie eines Netzes (die Zuordnung von Verbindungen zu Knoten) muss abhängig von seiner Aufgabe gut durchdacht sein. Nach der Konstruktion eines Netzes folgt die Trainingsphase, in der das Netz „lernt“. Theoretisch kann ein Netz durch folgende Methoden lernen:

Entwicklung neuer Verbindungen
Löschen existierender Verbindungen
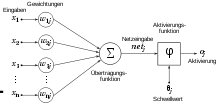
Ändern der Gewichtung (der Gewichte $w_{ij}$ von Neuron $j$ zu Neuron $i$ )
Anpassen der Schwellenwerte der Neuronen, sofern diese Schwellenwerte besitzen
Hinzufügen oder Löschen von Neuronen
Modifikation von Aktivierungs-, Propagierungs- oder Ausgabefunktion

Außerdem verändert sich das Lernverhalten bei Veränderung der Aktivierungsfunktion der Neuronen oder der Lernrate des Netzes. Praktisch gesehen „lernt“ ein Netz hauptsächlich durch Modifikation der Gewichte der Neuronen. Eine Anpassung des Schwellwertes kann hierbei durch ein on-Neuron miterledigt werden. Dadurch sind KNNs in der Lage, komplizierte nichtlineare Funktionen über einen „Lern“-Algorithmus, der durch iterative oder rekursive Vorgehensweise aus vorhandenen Ein- und gewünschten Ausgangswerten alle Parameter der Funktion zu bestimmen versucht, zu erlernen. KNNs sind dabei eine Realisierung des konnektionistischen Paradigmas, da die Funktion aus vielen einfachen gleichartigen Teilen besteht. Erst in ihrer Summe kann das Verhalten im Zusammenspiel sehr vieler beteiligter Teile komplex werden. Neuronale Netze stellen von der Berechenbarkeit her ein äquivalentes Modell zur Turingmaschine dar, falls sie deterministisch beschrieben werden und Rückkopplungen erlaubt sind.[1] D.h. zu jedem Netz gibt es mindestens eine Turingmaschine und zu jeder Turingmaschine gibt es mindestens ein Netz mit Rückkopplung. Bei einer stochastischen Beschreibung ist dies nicht der Fall. Rekurrente Netze sind damit die ausdrucksstärkste Form (Typ 0 in der Chomsky-Hierarchie).

Geschichtliche Entwicklung

Das Interesse für künstliche neuronale Netze setzte bereits in den frühen 1940er Jahren ein, also etwa gleichzeitig mit dem Einsatz programmierbarer Computer in angewandter Mathematik.[2]

Anfänge

Die Anfänge gehen auf Warren McCulloch und Walter Pitts zurück. Diese beschreiben 1943 Verknüpfungen von elementaren Einheiten als eine der Vernetzung von Neuronen ähnliche Art von Netz, mit dem sich praktisch jede logische oder arithmetische Funktion berechnen lassen könnte[3]. 1947 weisen sie darauf hin, dass ein solches Netz beispielsweise zur räumlichen Mustererkennung eingesetzt werden kann. 1949 formuliert Donald O. Hebb seine Hebbsche Lernregel, die in ihrer allgemeinen Form die meisten der künstlichen neuronalen Lernverfahren darstellt. Karl Lashley kommt 1950 zu der These, dass der Prozess der Informationsspeicherung im Gehirn verteilt auf verschiedene Untereinheiten realisiert wird.[4]

Erste Blütezeit

Im anschließenden Jahr, 1951, gelingt Marvin Minsky mit seiner Dissertationsarbeit der Bau des Neurocomputers Snarc, der seine Gewichte automatisch justieren kann, jedoch nicht praktisch einsetzbar ist.[4] 1956 treffen sich Wissenschaftler und Studenten auf der Dartmouth Conference. Diese Konferenz gilt als Geburtsstunde der Künstlichen Intelligenz als akademisches Fachgebiet.[5] Von 1957 bis 1958 entwickeln Frank Rosenblatt und Charles Wightman den ersten erfolgreichen Neurocomputer, mit dem Namen Mark I Perceptron. Der Computer konnte mit seinem 20 × 20 Pixel großen Bildsensor bereits einfache Ziffern erkennen. Im nachfolgenden Jahr formuliert Rosenblatt das Perceptron-Konvergenz-Theorem. 1960 stellen Bernard Widrow und Marcian E. Hoff das ADALINE (ADAptive LInear NEuron) vor.[6] Dieses Netz erreichte als erstes weite kommerzielle Verbreitung. Anwendung fand es in Analogtelefonen zur Echtzeit-Echofilterung. Das neuronale Netz lernte mit der Deltaregel. 1961 stellte Karl Steinbuch Techniken der assoziativen Speicherung vor. 1969 gaben Marvin Minsky und Seymour Papert eine genaue mathematische Analyse des Perceptrons.[7] Sie zeigten auf, dass wichtige Probleme nicht gelöst werden können. So sind unter anderem XOR-Operatoren nicht auflösbar und es gibt Probleme in der linearen Separierbarkeit. Die Folge war ein vorläufiges Ende der Forschungen auf dem Gebiet der neuronalen Netze, da die meisten Forschungsgelder gestrichen wurden.

Langsamer Wiederaufbau

1972 präsentiert Teuvo Kohonen den linearen Assoziator, ein Modell des Assoziativspeichers.[8] James A. Anderson beschreibt das Modell unabhängig von Kohonen aus neuropsychologischer Sicht im selben Jahr.[9] 1973 benutzt Christoph von der Malsburg ein Neuronenmodell, das nichtlinear ist. Bereits 1974 entwickelt Paul Werbos für seine Dissertation die Backpropagation bzw. die Fehlerrückführung. Das Modell bekam aber erst später eine größere Bedeutung. Ab 1976 entwickelt Stephen Grossberg mathematisch fundierte Modelle neuronaler Netze. Zusammen mit Gail Carpenter widmet er sich auch dem Problem, ein neuronales Netz lernfähig zu halten, ohne bereits Gelerntes zu zerstören. Sie formulieren ein Architekturkonzept für neuronale Netze, die Adaptive Resonanztheorie. 1982 beschreibt Teuvo Kohonen die nach ihm benannten selbstorganisierenden Karten. Im selben Jahr beschreibt John Hopfield das Modell der Hopfield-Netze. 1983 wird von Kunihiko Fukushima, S. Miyake und T. Ito das neuronale Modell Neocognitron vorgestellt. Das Modell ist eine Weiterentwicklung des 1975 entwickelten Cognitrons und dient zur Erkennung handgeschriebener Zeichen.

Renaissance

1985 veröffentlicht John Hopfield eine Lösung des Travelling Salesman Problems durch ein Hopfield-Netz. 1985 wird das Lernverfahren Backpropagation of Error als Verallgemeinerung der Delta-Regel durch die Parallel-Distributed-Processing-Gruppe separat entwickelt. Somit werden nicht linear separierbare Probleme durch mehrschichtige Perceptrons lösbar. Minskys Abschätzung war also widerlegt.

Neue Erfolge in Mustererkennungswettbewerben seit 2009

In jüngster Zeit erlebten neuronale Netze eine Wiedergeburt, da sie bei herausfordernden Anwendungen oft bessere Ergebnisse als konkurrierende Lernverfahren liefern. Zwischen 2009 und 2012 gewannen die rekurrenten bzw. tiefen vorwärtsgerichteten neuronalen Netze der Forschungsgruppe von Jürgen Schmidhuber am Schweizer KI Labor IDSIA eine Serie von acht internationalen Wettbewerben in den Bereichen Mustererkennung und maschinelles Lernen.[10] Insbesondere gewannen ihre rekurrenten LSTM-Netze[11][12] drei Wettbewerbe zur verbundenen Handschrifterkennung bei der 2009 Intl. Conf. on Document Analysis and Recognition (ICDAR) ohne eingebautes A-priori-Wissen über die drei verschiedenen zu lernenden Sprachen. Die LSTM-Netze erlernten gleichzeitige Segmentierung und Erkennung. Dies waren die ersten internationalen Wettbewerbe, die durch Deep Learning[13][14] oder durch rekurrente Netze gewonnen wurden.

Tiefe vorwärtsgerichtete Netze wie Kunihiko Fukushimas Konvolutionsnetz der 80er Jahre[15] sind heute wieder wichtig. Sie verfügen über alternierende Konvolutionslagen (convolutional layers) und Lagen von Neuronen, die mehrere Aktivierungen zusammenfassen (pooling layers[16]), um die räumliche Dimension zu reduzieren. Abgeschlossen wird ein solches Konvolutionsnetz in der Regel durch mehrere vollständig verbundene Schichten (englisch fully connected layers). Yann LeCuns Team von der New York University wandte den 1989 schon gut bekannten Backpropagation-Algorithmus auf solche Netze an.[17] Moderne Varianten verwenden sogenanntes max-pooling für die Zusammenfassung der Aktivierungen, das stets der stärksten Aktivierung den Vorzug gibt.[18] Schnelle GPU-Implementierungen dieser Kombination wurden 2011 durch Dan Ciresan und Kollegen in Schmidhubers Gruppe eingeführt.[19] Sie gewannen seither zahlreiche Wettbewerbe, u. a. die „ISBI 2012 Segmentation of Neuronal Structures in Electron Microscopy Stacks Challenge“[20] und den „ICPR 2012 Contest on Mitosis Detection in Breast Cancer Histological Images“.[21] Derartige Modelle erzielten auch die bisher besten Ergebnisse auf dem ImageNet Benchmark.[22][23] GPU-basierte max-pooling-Konvolutionsnetze waren auch die ersten künstlichen Mustererkenner mit übermenschlicher Performanz[24] in Wettbewerben wie der „IJCNN 2011 Traffic Sign Recognition Competition“.[25] In den letzten Jahren fand auch die Theorie der Zufallsmatrizen vermehrt Anwendung in der Erforschung von neuronalen Netzwerken.[26]

Topologie der Verbindungsnetze

Einschichtiges Netz

Zweischichtiges Netz

Rekurrentes Netz

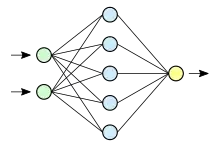
In künstlichen neuronalen Netzen bezeichnet die Topologie die Struktur des Netzes. Damit ist im Allgemeinen gemeint, wie viele künstliche Neuronen sich auf wie vielen Schichten befinden, und wie diese miteinander verbunden sind. Künstliche Neuronen können auf vielfältige Weise zu einem künstlichen neuronalen Netz verbunden werden. Dabei werden Neuronen bei vielen Modellen in hintereinander liegenden Schichten (englisch layers) angeordnet; bei einem Netz mit nur einer trainierbaren Neuronenschicht spricht man von einem einschichtigen Netz.

Unter Verwendung eines Graphen können die Neuronen als Knoten und ihre Verbindungen als Kanten dargestellt werden. Die Eingaben werden gelegentlich auch als Knoten dargestellt.

Die hinterste Schicht des Netzes, deren Neuronenausgaben meist als einzige außerhalb des Netzes sichtbar sind, wird Ausgabeschicht (englisch output layer) genannt. Davorliegende Schichten werden entsprechend als verdeckte Schicht (englisch hidden layer) bezeichnet.

Typische Strukturen

Die Struktur eines Netzes hängt unmittelbar mit dem verwendeten Lernverfahren zusammen und umgekehrt; so kann mit der Delta-Regel nur ein einschichtiges Netz trainiert werden, bei mehreren Schichten ist eine leichte Abwandlung vonnöten. Dabei müssen Netze nicht zwingend homogen sein: es existieren auch Kombinationen aus verschiedenen Modellen, um so unterschiedliche Vorteile zu kombinieren.

Es gibt reine feedforward-Netze, bei denen eine Schicht immer nur mit der nächsthöheren Schicht verbunden ist. Darüber hinaus gibt es Netze, in denen Verbindungen in beiden Richtungen erlaubt sind. Die passende Netzstruktur wird meist nach der Methode von Versuch und Irrtum gefunden, was durch evolutionäre Algorithmen und eine Fehlerrückführung unterstützt werden kann.

Einschichtiges feedforward-Netz: Einschichtige Netze mit der feedforward-Eigenschaft (englisch für vorwärts) sind die einfachsten Strukturen künstlicher neuronaler Netze. Sie besitzen lediglich eine Ausgabeschicht. Die feedforward-Eigenschaft besagt, dass Neuronenausgaben nur in Verarbeitungsrichtung geleitet werden und nicht durch eine rekurrente Kante zurückgeführt werden können (azyklischer, gerichteter Graph).
Mehrschichtiges feedforward-Netz: Mehrschichtige Netze besitzen neben der Ausgabeschicht auch verdeckte Schichten, deren Ausgabe wie beschrieben, außerhalb des Netzes nicht sichtbar sind. Verdeckte Schichten verbessern die Abstraktion solcher Netze. So kann erst das mehrschichtige Perzeptron das XOR-Problem lösen.
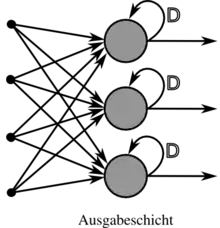
Rekurrentes Netz: Rekurrente Netze besitzen im Gegensatz dazu auch rückgerichtete (rekurrente) Kanten (englisch feedback loops) und enthalten somit eine Rückkopplung. Solche Kanten werden dann immer mit einer Zeitverzögerung (in der Systemtheorie als Verzögerungsglied bezeichnet) versehen, sodass bei einer schrittweisen Verarbeitung die Neuronenausgaben der vergangenen Einheit wieder als Eingaben angelegt werden können. Diese Rückkopplungen ermöglichen einem Netz ein dynamisches Verhalten und statten es mit einem Gedächtnis aus.

In bestimmten Gehirnregionen von Säugetieren – und auch anderen Wirbeltieren, etwa Singvögeln – werden nicht nur in Entwicklungsstadien, sondern noch im Erwachsenenalter Neuronen neugebildet und in das neuronale Netz integriert (siehe adulte Neurogenese, insbesondere im Hippocampus). Im Versuch, solche Prozesse in neuronalen Netzen künstlich nachzubilden, stößt die Modellierung an Grenzen. Zwar kann ein evolutionärer Algorithmus bestimmen, ähnlich einem Moore-Automaten, wie häufig ein Neuron aktiviert werden muss, damit sich in der Umgebung neue Neuronen ausbilden. Jedoch muss hier zusätzlich auch festgelegt werden, wie die neuen Neuronen in das vorhandene Netz integriert werden sollen. Künstliche neuronale Netze dieser Art müssen zwangsläufig darauf verzichten, in Schichten aufgebaut zu sein. Sie benötigen eine völlig freie Struktur, für die bestenfalls der Raum begrenzt werden kann, in dem sich die Neuronen befinden dürfen.

Anwendung

Seine besonderen Eigenschaften machen das KNN bei allen Anwendungen interessant, bei denen kein oder nur geringes explizites (systematisches) Wissen über das zu lösende Problem vorliegt. Dies sind z. B. die Texterkennung, Spracherkennung, Bilderkennung und Gesichtserkennung, bei denen einige Hunderttausend bis Millionen Bildpunkte in eine im Vergleich dazu geringe Anzahl von erlaubten Ergebnissen überführt werden müssen.

Auch in der Regelungstechnik kommen KNN zum Einsatz, um herkömmliche Regler zu ersetzen oder ihnen Sollwerte vorzugeben, die das Netz aus einer selbst entwickelten Prognose über den Prozessverlauf ermittelt hat. So können auch Fuzzy-Systeme durch eine bidirektionale Umwandlung in neuronale Netze lernfähig gestaltet werden.

Die Anwendungsmöglichkeiten sind aber nicht auf techniknahe Gebiete begrenzt: Bei der Vorhersage von Veränderungen in komplexen Systemen werden KNNs unterstützend hinzugezogen, z. B. zur Früherkennung sich abzeichnender Tornados oder aber auch zur Abschätzung der weiteren Entwicklung wirtschaftlicher Prozesse.

Zu den Anwendungsgebieten von KNNs gehören insbesondere:

Regelung und Analyse komplexer Prozesse
Frühwarnsysteme
Fehlererkennung
Optimierung
Zeitreihenanalyse (Wetter, Aktien usw.)
Sprachsynthese
Klangsynthese
Klassifikation
Bildverarbeitung und Mustererkennung
Informatik: Bei Robotik, virtuellen Agenten und KI-Modulen in Spielen und Simulationen
Medizinische Diagnostik, Epidemiologie und Biometrie
Strukturgleichungsmodell zum Modellieren von sozialen oder betriebswirtschaftlichen Zusammenhängen

Trotz dieser sehr großen Spanne an Anwendungsgebieten gibt es Bereiche, die KNNs aufgrund ihrer Natur nicht abdecken können, beispielsweise:[27]

Vorhersage von Zufalls- oder Pseudozufalls-Zahlen
Faktorisierung von großen Zahlen
Bestimmung, ob eine große Zahl prim ist
Entschlüsseln von verschlüsselten Texten

Implementierungen

TensorFlow – Programmbibliothek
SNNS – Stuttgarter Neuronale-Netze-Simulator
EpsiloNN neuronale Beschreibungssprache der Universität Ulm
OpenNN

Biologische Motivation

Während das Gehirn zur massiven Parallelverarbeitung in der Lage ist, arbeiten die meisten heutigen Computersysteme nur sequentiell (bzw. partiell parallel eines Rechners). Es gibt jedoch auch erste Prototypen neuronaler Rechnerarchitekturen, sozusagen den neuronalen Chip, für die das Forschungsgebiet der künstlichen neuronalen Netze die theoretischen Grundlagen bereitstellt. Dabei werden die physiologischen Vorgänge im Gehirn jedoch nicht nachgebildet, sondern nur die Architektur der massiv parallelen Analog-Addierer in Silizium nachgebaut, was gegenüber einer Software-Emulation eine bessere Leistung verspricht.

Klassen und Typen von KNN

Grundsätzlich unterscheiden sich die Klassen der Netze vorwiegend durch die unterschiedlichen Netztopologien und Verbindungsarten, so zum Beispiel einschichtige, mehrschichtige, Feedforward- oder Feedback-Netze.

McCulloch-Pitts-Netze
Lernmatrix
Perzeptron
- Adaline-Modell
- Convolutional Neural Network (CNN)
Self-Organizing Maps (auch Kohonen-Netze) (SOM)
Growing Neural Gas (GNG)
Lernende Vektorquantisierung (LVQ)
Boltzmann-Maschine
Cascade-Correlation-Netze
Counterpropagation Netze
Probabilistische neuronale Netze
Radiale Basisfunktions-Netze (RBF)
Adaptive Resonanztheorie (ART)
Neocognitron
Spiking Neural Networks (SNN)
- Pulscodierte neuronale Netze (PCNN)
Time Delay Neural Networks (TDNNs)
Rekurrente neuronale Netze (RNNs)
- Bidirektionaler Assoziativspeicher (BAM)
  - Hopfield-Netze
- Elman-Netze (auch Simple recurrent network, SRN)
- Jordan-Netze
Oszillierendes neuronales Netz
Residuale neuronale Netze

Aktivierungsfunktion

Jede verdeckte Schicht und die Ausgabeschicht bzw. deren Neuronen verfügen über eine (eigene) Aktivierungsfunktion. Diese können linear oder nicht-linear sein. Nicht-lineare Aktivierungsfunktionen machen das Netz besonders mächtig.[28]

Lernverfahren

Lernverfahren dienen dazu, ein neuronales Netz so zu modifizieren, dass es für bestimmte Eingangsmuster zugehörige Ausgabemuster erzeugt. Dies geschieht grundsätzlich auf drei verschiedenen Wegen.

Überwachtes Lernen (supervised learning)

Beim Überwachten Lernen wird dem KNN ein Eingangsmuster gegeben und die Ausgabe, die das neuronale Netz in seinem aktuellen Zustand produziert, mit dem Wert verglichen, den es eigentlich ausgeben soll. Durch Vergleich von Soll- und Istausgabe kann auf die vorzunehmenden Änderungen der Netzkonfiguration geschlossen werden. Bei einlagigen Perzeptrons kann die Delta-Regel (auch Perzeptron-Lernregel) angewendet werden. Mehrlagige Perzeptrons werden in der Regel mit Backpropagation trainiert, was eine Verallgemeinerung der Delta-Regel darstellt.

Unüberwachtes Lernen (unsupervised learning)

Das Unüberwachte Lernen erfolgt ausschließlich durch Eingabe der zu lernenden Muster. Das neuronale Netz verändert sich entsprechend den Eingabemustern von selbst. Hierbei gibt es folgende Lernregeln:

Bestärkendes Lernen (reinforced learning)

Es ist nicht immer möglich, zu jedem Eingabedatensatz den passenden Ausgabedatensatz zum Trainieren zur Verfügung zu haben. Zum Beispiel kann man einem Agenten, der sich in einer fremden Umgebung zurechtfinden muss – etwa einem Roboter auf dem Mars – nicht zu jedem Zeitpunkt sagen, welche Aktion jeweils die beste ist. Aber man kann dem Agenten eine Aufgabe stellen, die dieser selbstständig lösen soll. Nach einem Testlauf, der aus mehreren Zeitschritten besteht, kann der Agent bewertet werden. Aufgrund dieser Bewertung kann eine Agentenfunktion gelernt werden.

Der Lernschritt kann durch eine Vielzahl von Techniken vollzogen werden. Unter anderem können hier auch künstliche neuronale Netze zum Einsatz kommen.

Stochastisches Lernen

Simulierte Abkühlung (Simulated Annealing)

Allgemeine Probleme

Die Hauptnachteile von KNN sind gegenwärtig:

Das Trainieren von KNN (im Terminus der Statistik: Das Schätzen der im Modell enthaltenen Parameter) führt in der Regel zu hochdimensionalen, nichtlinearen Optimierungsproblemen. Die prinzipielle Schwierigkeit bei der Lösung dieser Probleme besteht in der Praxis häufig darin, dass man nicht sicher sein kann, ob man das globale Optimum gefunden hat oder nur ein lokales. Obgleich in der Mathematik eine Fülle relativ schnell konvergierender lokaler Optimierungsverfahren entwickelt wurden (beispielsweise Quasi-Newton-Verfahren: BFGS, DFP usw.), finden auch diese selten optimale Lösungen. Eine zeitaufwändige Näherung an die globale Lösung erreicht man gegebenenfalls durch die vielfache Wiederholung der Optimierung mit immer neuen Startwerten.
Es müssen Trainingsdaten gesammelt oder manuell erzeugt werden. Dieser Vorgang kann sehr schwierig sein, da man verhindern muss, dass das Netz Eigenschaften der Muster lernt, die zwar auf dem Trainingsset mit dem Ergebnis in irgendeiner Weise korreliert sind, die aber in anderen Situationen nicht zur Entscheidung herangezogen werden können oder sollen. Wenn beispielsweise die Helligkeit von Trainingsbildern bestimmte Muster aufweist, dann 'achtet' das Netz unter Umständen nicht mehr auf die gewünschten Eigenschaften, sondern klassifiziert die Daten nur noch aufgrund der Helligkeit. Im sozialen Bereich besteht z. B. die Gefahr, durch einseitig ausgewählte Testdaten bestehende Diskriminierungen (etwa aufgrund des Geschlechts oder der Herkunft) fortzuschreiben, ohne die eigentlich angezielten Kriterien (etwa Kreditwürdigkeit) ausreichend zu berücksichtigen.
Bei Anwendung einer heuristischen Vorgehensweise bei der Netzspezifikation neigen KNN dazu, die Trainingsdaten einfach auswendig zu lernen, infolge Übergeneralisierung bzw. Überanpassung (englisch overfitting).[29] Wenn dies geschieht, können die Netze nicht mehr auf neue Daten verallgemeinern. Um eine Überanpassung zu vermeiden, muss die Netzarchitektur mit Bedacht gewählt werden. In ähnlicher Weise besteht diese Problematik auch bei vielen anderen statistischen Verfahren und wird als Verzerrung-Varianz-Dilemma bezeichnet. Verbesserte Verfahren setzen Boosting, Support-Vector-Maschinen oder Regularisierung ein, um diesem Problem zu begegnen.
Die Kodierung der Trainingsdaten muss problemangepasst und nach Möglichkeit redundanzfrei gewählt werden. In welcher Form die zu lernenden Daten dem Netz präsentiert werden, hat einen großen Einfluss auf die Lerngeschwindigkeit, sowie darauf, ob das Problem überhaupt von einem Netz gelernt werden kann. Gute Beispiele hierfür sind Sprachdaten, Musikdaten oder auch Texte. Das einfache Einspeisen von Zahlen, beispielsweise aus einer .wav-Datei für Sprache, führt selten zu einem erfolgreichen Ergebnis. Je präziser das Problem allein durch die Vorverarbeitung und Kodierung gestellt wird, desto erfolgreicher kann ein KNN dieses verarbeiten.
Die Vorbelegung der Gewichte spielt eine wichtige Rolle. Als Beispiel sei ein 3-schichtiges Feed-Forward-Netz mit einem Eingabeneuron (plus ein Bias-Neuron) und einem Ausgabeneuron und einer verdeckten Schicht mit N Neuronen (plus ein Bias-Neuron) angenommen. Die Aktivierungsfunktion des Eingabeneurons sei die Identität. Die Aktivierungsfunktion der verdeckten Schicht sei die Tanh-Funktion. Die Aktivierungsfunktion der Ausgabeschicht sei die logistische Sigmoide. Das Netz kann maximal eine Sinusfunktion mit N lokalen Extrema im Intervall von 0 bis 1 lernen. Wenn es diese Sinusfunktion gelernt hat, kann es mit dieser Gewichtsbelegung jede beliebige Funktion – die nicht mehr lokale Extrema als diese Sinusfunktion – mit möglicherweise exponentieller Beschleunigung – lernen (unabhängig vom Lernalgorithmus). Hier sei der einfachste Backpropagation ohne Momentum verwendet. Glücklicherweise kann man die Gewichte für solch eine Sinusfunktion leicht berechnen, ohne dass das Netz das erst lernen muss: Verdeckte Schicht : $i=0\ldots N-1$ , x = i % 2 == 0 ? 1 : -1 , $w_{0i}=x\cdot \pi \cdot (N-0{,}5),w_{li}=-x\cdot i\cdot \pi$ ; Ausgabeschicht : $w_{j}=1$ .

Filmische Dokumentationen

Siehe auch

Literatur

Johann Gasteiger, Jure Zupan: Neural Networks in Chemistry and Drug Design. Wiley-VCH, Weinheim NY u. a. 1999, ISBN 3-527-29779-0.
Simon Haykin: Neural Networks. A Comprehensive Foundation. 2. edition, international edition = Reprint. Prentice-Hall, Upper Saddle River NJ u. a. 1999, ISBN 0-13-273350-1.
John Hertz, Anders Krogh, Richard G. Palmer: Introduction to the Theory of Neural Computation. Nachdruck. Addison-Wesley, Reading MA u. a. 1999, ISBN 0-201-51560-1 (Santa Fé Institute studies in the sciences of complexity. Lecture notes 1 = Computation and neural systems series).
Teuvo Kohonen: Self Organizing Maps. 3. edition. Springer, Berlin u. a. 2001, ISBN 3-540-67921-9 (Springer Series in Information Sciences 30 = Physics and Astronomy online Library).
Rudolf Kruse, Christian Borgelt, Frank Klawonn, Christian Moewes, Georg Ruß, Matthias Steinbrecher: Computational Intelligence. 1. Auflage, Vieweg+Teubner Verlag/Springer Fachmedien Wiesbaden, 2011, ISBN 978-3-8348-1275-9.
Burkhard Lenze: Einführung in die Mathematik neuronaler Netze. Mit C-Anwendungsprogrammen im Internet. 3. durchgesehene und überarbeitete Auflage. Logos-Verlag, Berlin 2009, ISBN 3-89722-021-0.
André Lucas: Schätzung und Spezifikation ökonometrischer neuronaler Netze. Eul, Lohmar 2003, ISBN 3-89936-183-0 (Reihe: Quantitative Ökonomie 138), (Zugleich: Köln, Univ., Diss., 2002).
Heinz Rehkugler, Hans Georg Zimmermann: Neuronale Netze in der Ökonomie. Grundlagen und finanzwirtschaftliche Anwendungen. Vahlen, München 1994, ISBN 3-800-61871-0.
Günter Daniel Rey, Karl F. Wender: Neuronale Netze. Eine Einführung in die Grundlagen, Anwendungen und Datenauswertung. Hogrefe AG, Bern 2018, dritte Auflage, ISBN 978-34568-5796-1 (Psychologie Lehrbuch).
Helge Ritter, Thomas Martinetz, Klaus Schulten: Neural Computation and Self-Organizing Maps. An Introduction. Addison-Wesley, Reading MA 1992, ISBN 0-201-55442-9 (Computation and neural Systems Series).
Raúl Rojas: Theorie der Neuronalen Netze. Eine systematische Einführung. 4. korrigierter Nachdruck. Springer, Berlin u. a. 1996, ISBN 3-540-56353-9 (Springer-Lehrbuch).
Andreas Zell: Simulation neuronaler Netze. 4. unveränderter Nachdruck. Oldenbourg, München u. a. 2003, ISBN 3-486-24350-0.

Weblinks

Commons: Künstliches neuronales Netz – Album mit Bildern, Videos und Audiodateien

Einführung in die Grundlagen und Anwendungen neuronaler Netze
"Der Blick in Neuronale Netze, 1. Juli 2019, in: Fraunhofer-Institut für Nachrichtentechnik
"Neuronale Netze: Einführung", Nina Schaaf, 14. Januar 2020, in: Informatik Aktuell (Magazin)
Ein kleiner Überblick über Neuronale Netze – Grundlagenskript zu zahlreichen Arten / Lernprinzipien neuronaler Netze, viele Abbildungen, einfach geschrieben, ca. 200 Seiten (PDF).
Gute Einführung in neuronale Netze (englisch)

Einzelnachweise

— (Memento vom 2. Mai 2013 im Internet Archive)
http://www.dkriesel.com/science/neural_networks, Stand: 14. April 2016
Warren S. McCulloch und Walter Pitts: A logical calculus of the ideas immanent in nervous activity. Hrsg.: Bulletin of Mathematical Biophysics. Vol. 5 Auflage. Kluwer Academic Publishers, 1943, S. 115–133, doi:10.1007/BF02478259.
Neuronale Netze - Einführung. Abgerufen am 5. September 2015 (englisch).
Erhard Konrad: Zur Geschichte der Künstlichen Intelligenz in der Bundesrepublik Deutschland (PDF; 86 kB), abgerufen am 23. Mai 2019.
Bernhard Widrow, Marcian Hoff: Adaptive switching circuits. In: Proceedings WESCON. 1960, ZDB-ID 267416-6, S. 96–104.
Marvin Minsky, Seymour Papert: Perceptrons. An Introduction to Computational Geometry. MIT Press, Cambridge MA u. a. 1969.
Teuvo Kohonen: Correlation matrix memories. In: IEEE transactions on computers. C-21, 1972, ISSN 0018-9340, S. 353–359.
James A. Anderson: A simple neural network generating an interactive memory. In: Mathematical Biosciences. 14, 1972, ISSN 0025-5564, S. 197–220.
2012 Kurzweil AI Interview (Memento vom 31. August 2018 im Internet Archive) mit Jürgen Schmidhuber zu den acht Wettbewerben, die sein Deep Learning Team zwischen 2009 und 2012 gewann
Alex Graves, Jürgen Schmidhuber: Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks. In: Yoshua Bengio, Dale Schuurmans, John Lafferty, Chris K. I. Williams, Aron Culotta (Hrsg.): Advances in Neural Information Processing Systems 22 (NIPS'22), December 7th–10th, 2009, Vancouver, BC. Neural Information Processing Systems (NIPS) Foundation, 2009, S. 545–552
A. Graves, M. Liwicki, S. Fernandez, R. Bertolami, H. Bunke, J. Schmidhuber: A Novel Connectionist System for Improved Unconstrained Handwriting Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, Band 31, Nr. 5, 2009.
Y. Bengio: Learning Deep Architectures for AI. (Memento vom 21. März 2014 im Internet Archive) Now Publishers, 2009.
Jürgen Schmidhuber: My First Deep Learning System of 1991 + Deep Learning Timeline 1962–2013.
K. Fukushima: Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. In: Biological Cybernetics. 36, Nr. 4, 1980, S. 93–202. doi:10.1007/BF00344251.
Dominik Scherer, Andreas Müller, Sven Behnke: Evaluation of Pooling Operations in Convolutional Architectures for Object Recognition. In: Artificial Neural Networks – ICANN 2010 (= Lecture Notes in Computer Science). Springer Berlin Heidelberg, 2010, ISBN 978-3-642-15825-4, S. 92–101, doi:10.1007/978-3-642-15825-4_10 (springer.com [abgerufen am 26. August 2019]).
Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, L. D. Jackel: Backpropagation Applied to Handwritten Zip Code Recognition. In: Neural Computation. Band 1, 1989. S. 541–551.
M. Riesenhuber, T. Poggio: Hierarchical models of object recognition in cortex. In: Nature Neuroscience. 1999.
D. C. Ciresan, U. Meier, J. Masci, L. M. Gambardella, J. Schmidhuber: Flexible, High Performance Convolutional Neural Networks for Image Classification. International Joint Conference on Artificial Intelligence (IJCAI-2011, Barcelona), 2011.
D. Ciresan, A. Giusti, L. Gambardella, J. Schmidhuber: Deep Neural Networks Segment Neuronal Membranes in Electron Microscopy Images. In: Advances in Neural Information Processing Systems (NIPS 2012), Lake Tahoe, 2012.
D. Ciresan, A. Giusti, L. Gambardella, J. Schmidhuber: Mitosis Detection in Breast Cancer Histology Images using Deep Neural Networks. MICCAI 2013.
A. Krizhevsky, I. Sutskever, G. E. Hinton: ImageNet Classification with Deep Convolutional Neural Networks. NIPS 25, MIT Press, 2012.
M. D. Zeiler, R. Fergus: Visualizing and Understanding Convolutional Networks. 2013. arxiv:1311.2901
D. C. Ciresan, U. Meier, J. Schmidhuber: Multi-column Deep Neural Networks for Image Classification. IEEE Conf. on Computer Vision and Pattern Recognition CVPR 2012.
D. C. Ciresan, U. Meier, J. Masci, J. Schmidhuber: Multi-Column Deep Neural Network for Traffic Sign Classification. Neural Networks, 2012.
J. Pennington und Y. Bahri: Geometry of Neural Network Loss Surfaces via Random Matrix Theory. In: ICML. 2017 (semanticscholar.org).
Neural Networks FAQ. Abgerufen am 24. Juli 2019 (englisch).
Neural Networks FAQ. Abgerufen am 5. September 2015 (englisch).
Johannes Merkert: Ein künstliches neuronales Netz selbst gebaut. In: c't. Abgerufen am 24. Mai 2016.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] — (Memento vom 2. Mai 2013 im Internet Archive)

[2] ttp://www.dkriesel.com/science/neural_networks, Stand: 14. April 2016

[3] Warren S. McCulloch und Walter Pitts: A logical calculus of the ideas immanent in nervous activity. Hrsg.: Bulletin of Mathematical Biophysics. Vol. 5 Auflage. Kluwer Academic Publishers, 1943, S. 115–133, doi:10.1007/BF02478259.

[chemgapedia-4] Neuronale Netze - Einführung. Abgerufen am 5. September 2015 (englisch).

[5] Erhard Konrad: Zur Geschichte der Künstlichen Intelligenz in der Bundesrepublik Deutschland (PDF; 86 kB), abgerufen am 23. Mai 2019.

[6] Bernhard Widrow, Marcian Hoff: Adaptive switching circuits. In: Proceedings WESCON. 1960, ZDB-ID 267416-6, S. 96–104.

[7] Marvin Minsky, Seymour Papert: Perceptrons. An Introduction to Computational Geometry. MIT Press, Cambridge MA u. a. 1969.

[8] Teuvo Kohonen: Correlation matrix memories. In: IEEE transactions on computers. C-21, 1972, ISSN 0018-9340, S. 353–359.

[9] James A. Anderson: A simple neural network generating an interactive memory. In: Mathematical Biosciences. 14, 1972, ISSN 0025-5564, S. 197–220.

[10] 2012 Kurzweil AI Interview (Memento vom 31. August 2018 im Internet Archive) mit Jürgen Schmidhuber zu den acht Wettbewerben, die sein Deep Learning Team zwischen 2009 und 2012 gewann

[11] Alex Graves, Jürgen Schmidhuber: Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks. In: Yoshua Bengio, Dale Schuurmans, John Lafferty, Chris K. I. Williams, Aron Culotta (Hrsg.): Advances in Neural Information Processing Systems 22 (NIPS'22), December 7th–10th, 2009, Vancouver, BC. Neural Information Processing Systems (NIPS) Foundation, 2009, S. 545–552

[12] A. Graves, M. Liwicki, S. Fernandez, R. Bertolami, H. Bunke, J. Schmidhuber: A Novel Connectionist System for Improved Unconstrained Handwriting Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, Band 31, Nr. 5, 2009.

[13] Y. Bengio: Learning Deep Architectures for AI. (Memento vom 21. März 2014 im Internet Archive) Now Publishers, 2009.

[timeline-14] Jürgen Schmidhuber: My First Deep Learning System of 1991 + Deep Learning Timeline 1962–2013.

[K._Fukushima._Neocognitron_1980-15] K. Fukushima: Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. In: Biological Cybernetics. 36, Nr. 4, 1980, S. 93–202. doi:10.1007/BF00344251.

[16] Dominik Scherer, Andreas Müller, Sven Behnke: Evaluation of Pooling Operations in Convolutional Architectures for Object Recognition. In: Artificial Neural Networks – ICANN 2010 (= Lecture Notes in Computer Science). Springer Berlin Heidelberg, 2010, ISBN 978-3-642-15825-4, S. 92–101, doi:10.1007/978-3-642-15825-4_10 (springer.com [abgerufen am 26. August 2019]).

[LeCun1989-17] Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard, L. D. Jackel: Backpropagation Applied to Handwritten Zip Code Recognition. In: Neural Computation. Band 1, 1989. S. 541–551.

[M_Riesenhuber,_1999-18] M. Riesenhuber, T. Poggio: Hierarchical models of object recognition in cortex. In: Nature Neuroscience. 1999.

[ciresan2011-19] D. C. Ciresan, U. Meier, J. Masci, L. M. Gambardella, J. Schmidhuber: Flexible, High Performance Convolutional Neural Networks for Image Classification. International Joint Conference on Artificial Intelligence (IJCAI-2011, Barcelona), 2011.

[D._Ciresan,_A._Giusti_2012-20] D. Ciresan, A. Giusti, L. Gambardella, J. Schmidhuber: Deep Neural Networks Segment Neuronal Membranes in Electron Microscopy Images. In: Advances in Neural Information Processing Systems (NIPS 2012), Lake Tahoe, 2012.

[D._Ciresan,_A._Giusti_2013-21] D. Ciresan, A. Giusti, L. Gambardella, J. Schmidhuber: Mitosis Detection in Breast Cancer Histology Images using Deep Neural Networks. MICCAI 2013.

[Krizhevsky2012-22] A. Krizhevsky, I. Sutskever, G. E. Hinton: ImageNet Classification with Deep Convolutional Neural Networks. NIPS 25, MIT Press, 2012.

[Zeiler2013-23] M. D. Zeiler, R. Fergus: Visualizing and Understanding Convolutional Networks. 2013. arxiv:1311.2901

[C._Ciresan,_U._Meier_2012-24] D. C. Ciresan, U. Meier, J. Schmidhuber: Multi-column Deep Neural Networks for Image Classification. IEEE Conf. on Computer Vision and Pattern Recognition CVPR 2012.

[25] D. C. Ciresan, U. Meier, J. Masci, J. Schmidhuber: Multi-Column Deep Neural Network for Traffic Sign Classification. Neural Networks, 2012.

[26] J. Pennington und Y. Bahri: Geometry of Neural Network Loss Surfaces via Random Matrix Theory. In: ICML. 2017 (semanticscholar.org).

[27] Neural Networks FAQ. Abgerufen am 24. Juli 2019 (englisch).

[28] Neural Networks FAQ. Abgerufen am 5. September 2015 (englisch).

[29] Johannes Merkert: Ein künstliches neuronales Netz selbst gebaut. In: c't. Abgerufen am 24. Mai 2016.