Zeitreihenanalyse

Die Zeitreihenanalyse befasst sich in der Statistik mit der inferenzstatistischen Analyse von Zeitreihen und der Vorhersage von Trends (Trendextrapolation) zu ihrer künftigen Entwicklung. Sie ist eine Spezialform der Regressionsanalyse.

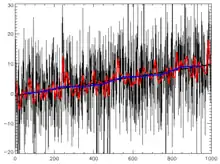
Beispiel für eine Zeitreihe: Random Walk mit Trend

Begriff der Zeitreihe

Eine Zeitreihe ist eine zeitlich geordnete Folge (meist aber keine Reihe im mathematischen Sinne) von Zahlen oder Beobachtungen, bei der sich die Anordnung der Merkmalsausprägungen zwingend aus dem Zeitablauf ergibt (etwa Aktienkurse, Börsenkurse allgemein, Bevölkerungsentwicklung, Preisindex, Wahlabsichtsbefragungen, Wetterdaten, Zinsindex).[1]

Die einzelnen Zeitpunkte werden zu einer Menge von Beobachtungszeitpunkten $T$ zusammengefasst, bei der für jeden Zeitpunkt $t\in T$ genau eine Beobachtung vorliegt.[2] Zeitreihen treten in allen Bereichen der Wissenschaft auf.

Zeitreihen: Nähere Begriffsbestimmung, Einteilung und Beispiele

Der Begriff Zeitreihe setzt voraus, dass Daten nicht kontinuierlich, sondern diskret aber in endlichen zeitlichen Abständen anfallen. Aus einem zeitkontinuierlichen Messsignal (oder der kontinuierlichen Aufzeichnung eines Messsignals, zum Beispiel mit einem analogen t-y-Schreiber oder einem analogen Magnetbandgerät) kann eine Zeitreihe durch Abtastung gewonnen werden.

Die Zeitpunkte, denen Datenpunkte zugeordnet werden, können äquidistant, also in konstanten Abständen (beispielsweise alle 5 Sekunden), in anderer Regelmäßigkeit (beispielsweise werktäglich) oder unregelmäßig angeordnet sein. Ein Datenpunkt kann aus einer einzelnen Zahl (skalare Werte, univariate Zeitreihe) oder aus einer Mehrzahl (Tupel) von Zahlenwerten (vektorielle Werte, multivariate Zeitreihe) bestehen. Jedoch müssen alle Datenpunkte in gleicher Weise aus Einzelwerten aufgebaut sein. Typische Zeitreihen entstehen aus dem Zusammenwirken regelhafter und zufälliger Ursachen. Die regelhaften Ursachen können periodisch (saisonal) variieren und/oder langfristige Trends enthalten. Zufällige Einflüsse werden oft als Rauschen bezeichnet.

Gegeben sei ein $T$ -dimensionaler Vektor von Zufallsvariablen $x_{1},x_{2},\dotsc ,x_{T}$ mit einer zugehörigen multivariaten Verteilung. Dies kann auch als eine Folge von Zufallsvariablen $\{x_{t}\}_{t=1}^{T}$ oder als stochastischer Prozess aufgefasst werden. Eine Stichprobe daraus ergibt als ein mögliches Ergebnis die T reellen Zahlen $\left\{x_{1}^{(1)},x_{2}^{(1)},\dotsc ,x_{T}^{(1)}\right\}$ . Selbst bei unendlich langer Beobachtung wäre $\left\{x_{t}^{(1)}\right\}_{t=1}^{\infty }$ nur eine einzige Realisierung des stochastischen Prozesses. Solch ein Prozess hat jedoch nicht nur eine Realisierung, sondern im Allgemeinen beliebig viele mit gleichen statistischen Eigenschaften. Eine Zeitreihe ist als eine Realisierung des datengenerierenden Prozesses definiert. Statt stochastische Prozesse der Dimension T anhand ihrer T-dimensionalen Verteilungsfunktion zu beschreiben, kann man ihn durch die Momente erster und zweiter Ordnung erfassen, also durch

T

Erwartungswerte:

\operatorname {E} (x_{i})\quad ,i=1,2,\dots ,T,

T

Varianzen:

\operatorname {Var} (x_{i})=\operatorname {E} ((x_{i}-\operatorname {E} (x_{i}))^{2})\quad ,i=1,2,\dotsc ,T,

{\frac {T(T-1)}{2}}

Kovarianzen:

\operatorname {Cov} (x_{i},x_{j})=\operatorname {E} ((x_{i}-\operatorname {E} (x_{i}))(x_{j}-\operatorname {E} (x_{j}))),\quad i<j.

Man spricht auch von Autokovarianzen, da es sich um Kovarianzen desselben Prozesses handelt. Im Spezialfall der mehrdimensionalen Normalverteilung des stochastischen Prozesses gilt, dass er durch die Momente erster und zweiter Ordnung eindeutig festgelegt ist. Für die statistische Inferenz mit Zeitreihen müssen Annahmen getroffen werden, da in der Praxis meist nur eine Realisierung des die Zeitreihe generierenden Prozesses vorliegt. Die Annahme der Ergodizität bedeutet, dass Stichprobenmomente, die aus einer endlichen Zeitreihe gewonnen werden, für $T\rightarrow \infty$ quasi gegen die Momente der Grundgesamtheit konvergieren.

Zeitreihen fallen in vielen Bereichen an:

in der Finanzmathematik und der Finanzwirtschaft: Börsenkurse; Liquiditätsentwicklungen
in der Ökonometrie: Bruttosozialprodukt, Arbeitslosenquote
in der Biometrie: EEG
in der Meteorologie: Temperatur, Windrichtung und -geschwindigkeit usw.
in der Fernerkundung: Vegetationsentwicklung und Aspektfolge
in der Polemologie (Quantitative Kriegs- und Friedensforschung): Dyadische Konfliktanalysen

Eine besonders komplexe (aber auch reichhaltige) Datensituation liegt vor, wenn man zeitabhängige Mikrodaten besitzt, also Personen- oder Haushaltsdaten für verschiedene Zeitpunkte. Hier spricht man allerdings nicht mehr von Zeitreihendaten, sondern von Trend-, Panel- oder Ereignisdaten, je nach ihrer Zeitstruktur.

Zeitreihenanalyse: Überblick

Ziele der Zeitreihenanalyse können sein

die kürzestmögliche Beschreibung einer historischen Zeitreihe
die Vorhersage von künftigen Zeitreihenwerten (Prognose) auf der Basis der Kenntnis ihrer bisherigen Werte (Wettervorhersage)
die Erkennung von Veränderungen in Zeitreihen (EEG oder EKG-Monitoring in der Medizin bei chirurgischen Eingriffen, Veränderung der globalen Vegetationsphänologie durch anthropogene Klimaänderungen)
die Eliminierung von seriellen oder saisonalen Abhängigkeiten oder Trends in Zeitreihen (Saisonbereinigung), um einfache Parameter wie Mittelwerte verlässlich zu schätzen

Die Vorgehensweise im Rahmen der Zeitreihenanalyse lässt sich in folgende Arbeitsphasen einteilen:

Identifikationsphase: Identifikation eines geeigneten Modells für die Modellierung der Zeitreihe
Schätzphase: Schätzung von geeigneten Parametern für das gewählte Modell
Diagnosephase: Diagnose und Evaluierung des geschätzten Modells
Einsatzphase: Einsatz des geschätzten und als geeignet befundenen Modells (insbesondere zu Prognosezwecken)

In den einzelnen Phasen ergeben sich Unterschiede, je nachdem ob man lineare Modelle zur Zeitreihenanalyse (Box-Jenkins-Methode, Komponentenmodell) oder nichtlineare Modelle zu Grunde legt. Im Folgenden wird beispielhaft auf die Box-Jenkins-Methode eingegangen.

Identifikationsphase

An erster Stelle sollte die graphische Darstellung der empirischen Zeitreihenwerte stehen. Dieses ist die einfachste und intuitivste Methode. Im Rahmen der graphischen Analyse lassen sich erste Schlüsse über das Vorliegen von Trends, Saisonalitäten, Ausreißern, Varianzinstationarität sowie sonstiger Auffälligkeiten ziehen. Stellt man einen stochastischen Trend (Instationarität) fest (entweder durch die graphische Analyse oder durch einen statistischen Test wie den erweiterter Dickey-Fuller-Test (englisch augmented Dickey-Fuller test, kurz ADF test)), der später durch eine Transformation der Zeitreihe (Differenzieren) bereinigt werden soll, so bietet sich eine Varianzstabilisierung (beispielsweise Box-Cox-Transformation) an. Die Varianzstabilisierung ist wichtig, da nach dem Differenzieren einer Zeitreihe negative Werte in der transformierten Zeitreihe vorkommen können.

Bevor weitergearbeitet werden kann, muss noch die grundsätzliche Frage geklärt werden, ob die Zeitreihe in einem deterministischen Modell (Trendmodell) oder einem stochastischen Modell abgebildet werden soll. Diese beiden Alternativen implizieren unterschiedliche Methoden der Trendbereinigung. Beim Trendmodell erfolgt die Bereinigung mittels einer Regressionsschätzung, beim stochastischen Modell mittels Differenzenbildung.

Schätzphase

In der Schätzphase werden die Modellparameter und -koeffizienten mit Hilfe unterschiedlicher Techniken geschätzt. Für das Trendmodell bietet sich die Kleinste-Quadrate-Schätzung, für die Modelle im Rahmen des Box-Jenkins-Ansatzes die Momentenmethode, die nichtlineare Kleinste-Quadrate-Schätzung und die Maximum-Likelihood-Methode für die Schätzung an.

Diagnosephase

In der Diagnosephase werden die Güte des Modells oder ggf. mehrere ausgewählte Modelle beurteilt. Dabei bietet sich folgende Vorgehensweise an:

1. Schritt: Prüfen, ob die geschätzten Koeffizienten signifikant von Null verschieden sind. Bei einzelnen Koeffizienten erfolgt dies mit Hilfe eines t-Tests, mehrere Koeffizienten zusammen werden mit einem F-Test untersucht.

2. Schritt: Verfährt man nach der Box-Jenkins-Methode, so ist zu prüfen, inwieweit die empirischen Autokorrelationskoeffizienten mit denen übereinstimmen, die sich theoretisch aufgrund der vorher geschätzten Koeffizienten ergeben müssten. Zusätzlich können die partiellen Autokorrelationskoeffizienten sowie das Spektrum analysiert werden.

3. Schritt: Schließlich erfolgt eine sorgfältige Analyse der Residuen. Die Residuen sollten keine Struktur mehr aufweisen. Dabei kann man die Zentriertheit der Residuen mit einem t-Test kontrollieren. Die Konstanz der Varianz kann visuell am Zeitreihengraphen oder durch Berechnung des Effekts verschiedener λ-Werte in einer Box-Cox-Transformation berechnet werden. Um die Autokorrelationsfreiheit der Residuen zu prüfen kann man jeden einzelnen Koeffizienten auf signifikanten Unterschied zu Null prüfen oder die ersten $n$ Koeffizienten gemeinsam auf Signifikanz zu Null testen. Um Letzteres zu klären kann auf die so genannten Portmanteau-Tests zurückgegriffen werden. Hierfür bieten sich beispielsweise Informationskriterien an.

Einsatzphase

In der Einsatzphase gilt es aus der in der Identifikationsphase aufgestellten und als brauchbar befundenen Modellgleichung eine Vorhersagegleichung zu formulieren. Dabei muss vorher ein Optimalitätskriterium festgelegt werden. Dafür kann die minimale mittlere quadratische Abweichung (englisch minimal mean squared error, kurz MMSE) genommen werden.

Methoden der Zeitreihenanalyse

Abbildung 1: Verfahren der Zeitreihenanalyse

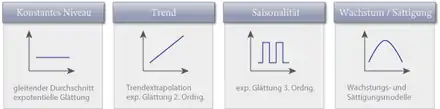
Die Verlaufsmuster von Zeitreihen können in verschiedene Komponenten zerlegt werden (Komponentenzerlegung). So gibt es systematische oder quasi-systematische Komponenten. Dazu gehören die Trendkomponente als allgemeine Grundrichtung der Zeitreihe, die Saisonkomponente als eine zyklische Bewegung innerhalb eines Jahres, die Zykluskomponente (bei ökonomischen Zeitreihen auch Konjunktur genannt) mit einer Periodenlänge von mehr als einem Jahr sowie eine Kalenderkomponente, die auf Kalenderunregelmäßigkeiten zurückzuführen ist. Als weitere Komponente tritt noch eine Rest- oder irreguläre Komponente auf. Hierunter fallen Ausreißer und Strukturbrüche, die durch historische Ereignisse erklärt werden können, sowie Zufallsschwankungen, deren Ursachen im Einzelnen nicht identifiziert werden können.

Die genannten Komponenten sind nicht direkt beobachtbar. Sie entspringen vielmehr der menschlichen Vorstellung. Somit stellt sich die Frage, wie man diese Komponenten modelliert.

Traditionelle Ansätze betrachten Zufallsschwankungen als strukturneutral und fassen die systematischen Komponenten als deterministische Funktionen der Zeit auf,

Y_{t}=\beta _{0}+\beta _{1}t+Z_{t}

.

In neueren Ansätzen haben Zufallschwankungen eine dominierende Rolle bei der Modellierung der systematischen Komponente. Damit wird die Zeitreihe durch einen stochastischen Prozess modelliert, wie einen MA(1)-Prozess:

Y_{t}=\theta _{1}Z_{t-1}+Z_{t}

.

Dabei ist $t$ der Zeitindex und $Z_{t}$ eine Zufallsvariable, für die die Eigenschaft weißes Rauschen angenommen werden kann. Einen dazu konträren Ansatz der Zeitreihenmodellierung stellt die Chaostheorie (siehe dazu Dimensionalität) dar.

In der Zeitreihenanalyse stehen einige allgemeine mathematische Instrumente zur Verfügung, wie Transformation (Box-Cox-Transformation), Aggregation, Regression, Filterung und gleitende Durchschnitte. Im Folgenden wird davon ausgegangen, dass die Zeitreihe als stochastischer Prozess modelliert werden kann. Dieser Ansatz wird auch als Box-Jenkins-Methode bezeichnet. Für stochastische Prozesse gibt es weitere spezielle Methoden und Instrumente. Hierzu zählen die:

Analyse im Frequenzbereich (Fourier-Theorie und Spektralanalyse),
Autokovarianz- und Autokorrelationsfunktion,
Partielle Autokorrelationsfunktion,
MA- und AR-Darstellung.

Inferenzstatistische Analyse von Zeitreihen

In der Inferenzstatistik schätzt man die Größe der untersuchten Effekte auf der Basis von Stichproben. Neben den schon genannten Verfahren, bei denen man inferenzstatistisch dann die Fehler der gefundenen Ergebnisse abschätzt, können komplexe Zeitreihen-Modelle spezifiziert und geschätzt werden. Dies wird vor allem in der Ökonometrie für ökonomische Modelle genutzt. Grundlage ist der Begriff des stochastischen Prozesses; hier ist insbesondere die Gruppe der ARMA-Prozesse zu erwähnen.

Ordinale Zeitreihenanalyse

Die ordinale Zeitreihenanalyse stellt ein relativ neues Verfahren zur qualitativen Untersuchung langer und komplexer Zeitreihen dar. Anstatt der Werte einer Zeitreihe wird die Ordnungsrelation zwischen den Werten, also das Auf und Ab, beschrieben. Dafür wird die Zeitreihe in ordinale Muster transformiert und anschließend die Verteilung dieser Muster statistisch analysiert, um so die Komplexität beziehungsweise den Informationsgehalt, der zugrundeliegenden Zeitreihe zu messen. Ein bekannter Komplexitätsparameter ist die Permutationsentropie, eingeführt im Jahr 2002 von Bandt und Pompe.

Neuronale Netze und die Verarbeitung von Zeitreihen

Beschäftigt man sich mit künstlichen neuronalen Netzwerken, erkennt man, dass der Modellierungsprozess sehr ähnlich zum ARIMA-Modell ist. In der Regel ist nur die Terminologie verschieden. Zur Prognose einer Zeitreihe mit einem Multilayer-Perceptron legt man ein gleitendes Zeitfenster mit n Werten der Vergangenheit über die Zeitreihe. Die Trainingsaufgabe besteht darin, aus n Werten in der Input-Schicht auf den nächsten Wert zu schließen. Das Training erfolgt anhand der bekannten Werte deren Zukunft zu prognostizieren, sozusagen aus sich selbst heraus. In der Regel sind es aber äußere Einflüsse aus einem (chaotischen) dynamischen System, die den Verlauf einer Zeitreihe (beobachtbare Werte des dynamischen Systems) beeinflussen. Um äußere Einflüsse in das Modell mit einzubeziehen, können zusätzliche Neuronen in die Inputschicht des Multilayer-Perceptrons eingegeben werden. Diese müssen ebenfalls in Form einer Zeitreihe vorliegen[3].

Siehe auch

Zeitreihe der Niederschlagssummen in Deutschland seit 1881

Literatur

Walter Assenmacher: Einführung in die Ökonometrie. 6. Auflage. Oldenbourg, München 2002, ISBN 3-486-25429-4.
Christoph Bandt & Bernd Pompe. (2002). Permutation Entropy: A Natural Complexity Measure for Time Series. In: Physical Review Letters. 88. 174102. doi:10.1103/PhysRevLett.88.174102
Walter Enders: Applied Economic Time Series. Wiley, Hoboken 2003, ISBN 0-471-23065-0.
James D. Hamilton: Time Series Analysis. Princeton University Press, Princeton, 1994, ISBN 0-691-04289-6.
Helmut Lütkepohl: New Introduction to Multiple Time Series Analysis. Springer-Verlag, Berlin, 2005, ISBN 978-3-540-40172-8.
Klaus Neusser: Zeitreihenanalyse in den Wirtschaftswissenschaften. 3. Auflage. Vieweg+Teubner, Wiesbaden 2011, ISBN 3-8348-1846-1.
Horst Rinne, Katja Specht: Zeitreihen. Statistische Modellierung, Schätzung und Prognose. Vahlen, München 2002, ISBN 3-8006-2877-5.
Rainer Schlittgen, Bernd Streitberg: Zeitreihenanalyse. 9. Auflage. Oldenbourg, München 2001, ISBN 3-486-25725-0.
Elmar Steurer: Prognose von 15 Zeitreihen der DGOR mit Neuronalen Netzen. In: Operations-Research-Spektrum. 18(2), S. 117–125. doi:10.1007/BF01539737
Helmut Thome: Zeitreihenanalyse. Eine Einführung für Sozialwissenschaftler und Historiker. Oldenbourg, München 2005, ISBN 3-486-57871-5.
Ruey S. Tsay: Analysis of Financial Time Series. Wiley, Hoboken 2005, ISBN 0-471-69074-0.

Software zur Durchführung von Zeitreihenanalysen

Eine Zeitreihenanalyse kann unter anderem mit den freien Softwarepaketen R, gretl, OpenNN und RapidMiner durchgeführt werden. Zu proprietären Lösungen gehören die Softwarepakete BOARD, Dataplore, EViews, Limdep, RATS, SPSS, Stata, SAS sowie WinRATS.

Weblinks

Open-Source Buch „A First Course on Time Series Analysis with SAS“ der Universität Würzburg

Einzelnachweise

Hans E. Büschgen, Das kleine Börsen-Lexikon, 2012, S. 1176
Rainer Schlittgen, Bernd Streitberg: Zeitreihenanalyse. Oldenbourg Verlag, 2001., ISBN 978-3-486-71096-0 (abgerufen über De Gruyter Online). S. 1
Dieter Meiller, Christian Schieder: Applied Machine learning: Predicting behaviour of industrial units from climate data In: Abraham A. P., Roth, J. & Peng, G. C. (Hrsg.): Multi Conference on Computer Science and Information Systems 2018, IADIS Press, S. 66–72, ISBN 978-989-8533-80-7

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Hans E. Büschgen, Das kleine Börsen-Lexikon, 2012, S. 1176

[2] Rainer Schlittgen, Bernd Streitberg: Zeitreihenanalyse. Oldenbourg Verlag, 2001., ISBN 978-3-486-71096-0 (abgerufen über De Gruyter Online). S. 1

[3] Dieter Meiller, Christian Schieder: Applied Machine learning: Predicting behaviour of industrial units from climate data In: Abraham A. P., Roth, J. & Peng, G. C. (Hrsg.): Multi Conference on Computer Science and Information Systems 2018, IADIS Press, S. 66–72, ISBN 978-989-8533-80-7