Neuroinformatik
Die Neuroinformatik ist ein Teilgebiet der Informatik und der Neurobiologie, das sich mit der Informationsverarbeitung in neuronalen Systemen befasst, um diese in technischen Systemen anzuwenden. Bei der Neuroinformatik handelt es sich um ein stark interdisziplinäres Forschungsgebiet im Schnittbereich zwischen KI-Forschung und Kognitionswissenschaft. In der Neuroinformatik geht es, ähnlich der neuronalen KI, um die innere Arbeitsweise des Gehirns. Dessen Arbeitsweise wird untersucht, indem man seine Grundbausteine, Neuronen und Synapsen, und deren Verschaltung simuliert.
Die Neuroinformatik ist ein Nachbargebiet der Computational Neuroscience, welche sich als Teilgebiet der Neurobiologie mit dem Verständnis biologischer neuronaler Systeme mittels mathematischer Modelle beschäftigt. Sie ist ferner zu unterscheiden von der im englischen Sprachraum als Neuroinformatics bezeichneten Disziplin, die sich mit der Organisation neurowissenschaftlicher Daten durch informatische Methoden beschäftigt.
Teilgebiete der Neuroinformatik
Neuronale Methoden werden vor allem dann eingesetzt, wenn es darum geht, aus schlechten oder verrauschten Daten Informationen zu gewinnen, aber auch Algorithmen, die sich neuen Situationen anpassen, also lernen, sind typisch für die Neuroinformatik. Dabei unterscheidet man grundsätzlich überwachtes Lernen und unüberwachtes Lernen, ein Kompromiss zwischen beiden Techniken ist das Reinforcement-Lernen. Assoziativspeicher sind eine besondere Anwendung neuronaler Methoden, und damit oft Forschungsgegenstand der Neuroinformatik. Viele Anwendungen für künstliche neuronale Netze finden sich auch in der Mustererkennung und vor allem im Bildverstehen.
Universitäten
Die Neuroinformatik ist ein relativ junger und kleiner Teil der Informatik, dennoch finden sich an vielen Universitäten Institute, Abteilungen oder Arbeitsgruppen für Neuroinformatik.
Biologische Grundlagen neuronaler Netze
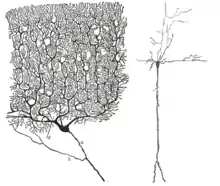
Nervenzellen finden sich im Körper aller Gewebetiere und werden als die funktionellen Grundeinheiten ihres Nervensystems aufgefasst. Ein typisches Neuron besteht aus drei Anteilen:
- afferente Zellfortsätze, Dendriten genannt und als Dendritenbaum verzweigt
- integrierender Zellkörper, Perikaryon genannt
- efferenter Zellfortsatz, Neurit oder auch Axon genannt, mit Abzweigungen (Kollaterale) und Aufzweigungen (Telodendron)
In einem Gehirn bilden die meist graubraunen Nervenzellkörper – als Ansammlung von Perikarya an ähnlichem Ort auch Kerne genannt – die sogenannte graue Substanz, und die helleren myelinisierten Nervenzellfortsätze – als Faserbündel von Axonen mit ähnlichem Verlauf auch Bahnen genannt – die sogenannte weiße Substanz. Die Dendritenbäume sind unterschiedlich stark verzweigt in der Nachbarschaft ausgebreitet und bilden so keinen makroskopisch auffälligen Aspekt.
Neuronen sind über Synapsen miteinander verknüpft an den Stellen, wo die Erregung von einem Neuron auf ein anderes übertragen wird. Das elektrische Signal wird dabei selten direkt weitergegeben, sondern meist mithilfe eines Neurotransmitters über den 20–30 nm synaptischen Spalt getragen. Bei solchen chemischen Synapsen unterscheidet man nach der Antwort der nachgeordneten (postsynaptischen) Zelle erregende exzitatorische von hemmenden inhibitorischen Synapsen. In einer Nervenzelle werden die durch verschiedene Synapsen hervorgerufenen Membranpotentialveränderungen (postsynaptische Potentiale) über dem Zellkörper summiert und am Axonhügel verrechnet. Wird dabei eine bestimmte Reizschwelle überschritten, so wird im Neuron ein Aktionspotential ausgelöst, das über sein Axon weitergeleitet wird.
Modellierung neuronaler Netze
Es gibt viele verschiedene Modelle, um Neuronale Netze zu modellieren. Ein Ansatz ist dabei, eine Reihe künstlicher Neuronen zu einem Netzwerk zu verschalten. Diese Neuronen können dabei je nach Fragestellung unterschiedlich nah an den biologischen Gegebenheiten orientiert sein. Es gibt aber auch viele andere Arten künstlicher neuronaler Netze:
- Netze mit Lehrer
- Perzeptron (Frank Rosenblatt) und vor allem das Multi-Layer-Perzeptron (MLP)
- Hetero-Assoziative-Netze
- Backpropagation
- Radiale-Basisfunktionen-Netze
- Netze mit Konkurrenz
- Selbstorganisierende Karten (werden auch als Kohonenkarten, nach Teuvo Kohonen, bezeichnet)
- K-Means Clusteranalyse
- Lernende Vektorquantisierung (LVQ)
- Adaptive Resonanz Theorie (ART)
- Hopfield-Netze (John Hopfield)
- Auto-Assoziation
- Boltzmann-Maschine (Terrence J. Sejnowski, Geoffrey Hinton)
Literatur
- Russell Beale, Tom Jackson: Neural Computing. An Introduction. Adam Hilger, Bristol u. a. 1990, ISBN 0-85274-262-2.
- Simon Haykin: Neural Networks. A Comprehensive Foundation. 2nd edition. Prentice Hall, Upper Saddle River NJ 1999, ISBN 0-13-273350-1.
- John Hertz, Anders Krogh, Richard G. Palmer: Introduction to the Theory of Neural Computation (= Santa Fe Institute Studies in the Sciences of Complexity. Lecture Notes. 1). Addison-Wesley, Redwood City CA u. a. 1991, ISBN 0-201-51560-1.
- Christof Koch: Biophysics of Computation. Information Processing in Single Neurons. Oxford University Press, New York NY 1999, ISBN 0-19-976055-1.
- Burkhard Lenze: Einführung in die Mathematik neuronaler Netze. 3., durchgesehene und überarbeitete Auflage. Logos, Berlin 2009, ISBN 978-3-89722-021-8.
- Raúl Rojas: Theorie der neuronalen Netze. Eine systematische Einführung. 4., korrigierter Nachdruck. Springer, Berlin u. a. 1996, ISBN 3-540-56353-9 (englische Ausgabe online).
- Philip D. Wasserman: Advanced methods in neural Computing. Van Nostrand Reinhold, New York NY 1993, ISBN 0-442-00461-3.
- Andreas Zell: Simulation neuronaler Netze. Addison-Wesley, Bonn u. a. 1994, ISBN 3-89319-554-8 (Zugleich: Stuttgart, Universität, Habilitations-Schrift, 1994).
- Peter-Michael Ziegler: IBM will das Gehirn nachbauen. heise. 2008. Abgerufen am 2. April 2014.