Selbstorganisierende Karte

Als Selbstorganisierende Karten, Kohonenkarten oder Kohonennetze (nach Teuvo Kohonen; englisch self-organizing map, SOM bzw. self-organizing feature map, SOFM) bezeichnet man eine Art von künstlichen neuronalen Netzen. Sie sind als unüberwachtes Lernverfahren ein leistungsfähiges Werkzeug des Data-Mining. Ihr Funktionsprinzip beruht auf der biologischen Erkenntnis, dass viele Strukturen im Gehirn eine lineare oder planare Topologie aufweisen. Die Signale des Eingangsraums, z. B. visuelle Reize, sind jedoch multidimensional.

Es stellt sich also die Frage, wie diese multidimensionalen Eindrücke durch planare Strukturen verarbeitet werden. Biologische Untersuchungen zeigen, dass die Eingangssignale so abgebildet werden, dass ähnliche Reize nahe beieinander liegen. Der Phasenraum der angelegten Reize wird also kartiert.

Wird nun ein Signal an diese Karte herangeführt, so werden nur diejenigen Gebiete der Karte erregt, die dem Signal ähnlich sind. Die Neuronenschicht wirkt als topologische Merkmalskarte, wenn die Lage der am stärksten erregten Neuronen in gesetzmäßiger und stetiger Weise mit wichtigen Signalmerkmalen korreliert ist.

Anwendung finden selbstorganisierende Karten zum Beispiel in der Computergrafik (als Quantisierungsalgorithmus zur Farbreduktion von Rastergrafikdaten) und zur Clusteranalyse.

Laterale Umfeldhemmung

Ein allgemeines Arbeitsprinzip des Nervensystems ist, dass aktive lokale Gruppen von Nervenzellen andere Gruppen ihrer Umgebung hemmen, und somit deren Aktivität unterdrücken (siehe laterale Hemmung). Die Aktivität einer Nervenzelle wird daher aus der Überlagerung des erregenden Eingangssignals und den hemmenden Beiträgen aller Schichtneuronen bestimmt. Da diese laterale Hemmung überall gilt, kommt es zu einem ständigen Wettbewerb um die Vorherrschaft. Der Verlauf der lateralen Hemmung ist für kurze Distanzen erregend/verstärkend und für lange Distanzen hemmend/schwächend. Es lässt sich zeigen, dass dieser Effekt ausreichend ist, eine Lokalisierung der Erregungsantwort in der Nähe der maximalen äußeren Erregung zu bewirken.

Struktur und Lernen

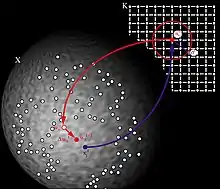
Ein Adaptionsschritt: Der Reiz 𝑣 zieht an dem Gewichtsvektor 𝑤 des am besten angepassten Neurons. Dieser Zug wird mit zunehmendem Abstand, gemessen im Competitive Layer vom besten Neuron, zunehmend schwächer. Einfach ausgedrückt, beult sich die Karte in Richtung des Reizes 𝑣 aus.

Eine Eingabeschicht mit 𝑛 Neuronen ist vollständig mit allen Neuronen innerhalb der Kohonenkarte (der sogenannte competitive layer), im Folgenden einfach Karte, verbunden. Jeder zu kartierende Eingangsreiz 𝑣 wird über die Verbindungen an jedes Neuron dieser Karte weitergegeben.

Die Verbindungsgewichte 𝑤 zwischen den Neuronen der Eingabeschicht und den Neuronen in der Karte definieren je einen Punkt im Eingangsraum der angelegten Reize 𝑣. Alle Neuronen innerhalb der Karte sind untereinander inhibitorisch (hemmend) vernetzt.

Die Abbildung zeigt einen Adaptionsschritt im Modell von Kohonen. Ein Reiz 𝑣 wird an das Netz angelegt.
Das Netz sucht das Erregungszentrum 𝑠 in der Karte, dessen Gewichtsvektor 𝑤 am nächsten zu 𝑣 liegt (kleinster Abstand).
Der Unterschied zwischen 𝑤 und 𝑣 wird in einem Adaptionsschritt verringert.
Die Neuronen nahe am Erregungszentrum 𝑠 werden auch adaptiert, aber umso weniger, je weiter sie vom Erregungszentrum entfernt sind.

Es ist gebräuchlich, aber nicht zwingend, sowohl für die Lernvektoren als auch für die Karte den euklidischen Abstand als Abstandsmaß zu verwenden.

Steht ein Satz verschiedener Trainingsdaten zur Verfügung, so ist eine Epoche im Training vollständig, wenn alle Reize genau einmal in zufälliger Reihenfolge an die Eingabeschicht angelegt worden sind. Das Training endet, wenn das Netz seinen stabilen Endzustand erreicht hat.

Das Lernen in einer selbstorganisierten Karte kann formal als iterativer Prozess beschrieben werden. Im Anfangszustand sind die Gewichtsvektoren der Neuronen zufällig im Netz verteilt und in jedem Lernschritt wird an das Netz ein Reiz angelegt. Die selbstorganisierende Karte verändert die Gewichtsvektoren der Neuronen entsprechend der Hebbschen Lernregel, sodass sich im Laufe der Zeit eine topografische Abbildung ergibt.

Training einer SOM im Beispiel

Die folgende Tabelle zeigt ein Netz, dessen Neuronen in einem Gitter angeordnet sind und zu Beginn zufällig im Raum verteilt sind. Es wird mit Eingabereizen aus dem Quadrat trainiert, die gleichverteilt sind.

Zufällig initialisiertes Netz	10 Trainingschritte	100 Trainingsschritte
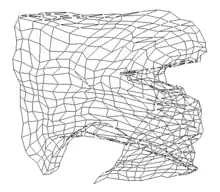1.000 Trainingsschritte	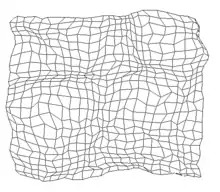10.000 Trainingsschritte	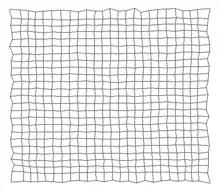100.000 Trainingsschritte

Formale Beschreibung des Trainings

Gegeben ist eine endliche Menge M von Trainingsstimuli m_i, die durch einen n-dimensionalen Vektor x_i spezifiziert sind:

M=\{m_{i}=(x_{i})\mid x_{i}\in X\subseteq \mathbb {R} ^{n},i=1,...,\mu _{M}\}

Weiterhin sei eine Menge von μ_N Neuronen gegeben, denen jeweils ein Gewichtsvektor w_i in X und eine Position k_i auf einer Kohonen-Karte zugeordnet wird, die im weiteren als zweidimensional angenommen wird. Die Kartendimension kann beliebig-dimensional gewählt werden, wobei Kartendimensionen kleiner-gleich drei zur Visualisierung von hochdimensionalen Zusammenhängen verwendet werden. Die Positionen auf der Karte sollen diskreten, quadratischen Gitterpunkten entsprechen (alternative Nachbarschaftstopologien wie z. B. hexagonale Topologien sind ebenfalls möglich), und jeder Gitterpunkt soll durch genau ein Neuron besetzt sein:

N=\{n_{i}=(w_{i},k_{i})\mid w_{i}\in X\subseteq \mathbb {R} ^{n},k_{i}\in K^{2},i=1,...,\mu _{N}\}

In der Lernphase wird aus der Menge der Stimuli zum Präsentationszeitpunkt t ein Element m_j^t gleichverteilt zufällig ausgewählt. Dieser Stimulus legt auf der Karte ein Gewinnerneuron n_s^t fest, das als Erregungszentrum bezeichnet wird. Es handelt sich dabei um genau das Neuron, dessen Gewichtsvektor w_s^t den geringsten Abstand im Raum X zu dem Stimulusvektor x_j^t besitzt, wobei eine Metrik d_X(.,.) des Inputraumes gegeben sei:

d_{X}(x_{j}^{t},w_{s}^{t})=min\{d_{X}(x_{j}^{t},w_{i}^{t})\mid i=1,...,\mu _{N}\}

Nachdem n_s^t ermittelt wurde, werden alle Neuronen n_i^t bestimmt, die neben dem Erregungszentrum ihre Gewichtsvektoren anpassen dürfen. Es handelt sich dabei um die Neuronen, deren Entfernung d_A(k_s, k_i) auf der Karte nicht größer ist als ein zeitabhängiger Schwellenwert, der als Entfernungsreichweite δ^t bezeichnet wird, wobei eine Metrik d_A(.,.) der Karte gegeben sei. Diese Neuronen werden in einer Teilmenge N^+t ⊂ N^t zusammengefasst:

N^{+t}=\{n_{i}=(w_{i},k_{i})\mid d_{A}(k_{s},k_{i})\leq \delta ^{t}\}

Im folgenden Adaptionsschritt wird auf alle Neuronen aus N^+t ein Lernschritt angewendet, der die Gewichtsvektoren verändert. Der Lernschritt ist interpretierbar als eine Verschiebung der Gewichtsvektoren in Richtung des Stimulusvektors x_j^t.

Es wird entsprechend dem Modell von Ritter et al. (1991) dabei die folgende Adaptionsregel verwendet:

w_{s}^{t+1}=w_{s}^{t}+\epsilon ^{t}\cdot h_{si}^{t}\cdot (x_{j}-w_{s}^{t})

mit den zeitabhängigen Parametergleichungen ε^t und h_si^t, die festgelegt werden als:

1) Die zeitabhängige Lernrate ε^t:

\epsilon ^{t}=\epsilon _{\text{start}}\cdot \left({\frac {\epsilon _{\text{end}}}{\epsilon _{\text{start}}}}\right)^{\frac {t}{t_{\text{max}}}}

mit der Startlernrate ε_start und ε_end als der Lernrate zum Ende des Verfahrens, d. h. nach t_max Stimuluspräsentationen.

2) Die zeitabhängige Entfernungsgewichtungsfunktion h_si^t:

h_{si}^{t}=e^{\frac {-d_{A}(k_{s},k_{i})^{2}}{2\cdot (\delta ^{t})^{2}}}

mit δ^t als dem Nachbarschafts- oder Adaptionsradius um das Gewinner-Neuron auf der Karte:

\delta ^{t}=\delta _{\text{start}}\cdot \left({\frac {\delta _{\text{end}}}{\delta _{\text{start}}}}\right)^{\frac {t}{t_{\text{max}}}}

mit dem Adaptionsradius δ_start zum Anfang des Verfahrens, und δ_end als dem Adaptionsradius zum Ende des Verfahrens.

Damit eine topologie-erhaltende Abbildung entsteht, d. h., dass benachbarte Punkte im Inputraum X auf benachbarte Punkte auf der Karte abgebildet werden, müssen zwei Faktoren berücksichtigt werden:

Die topologische Nachbarschaft h_si^t um das Erregungszentrum muss anfangs groß gewählt und im Laufe des Verfahrens verkleinert werden.
Die Adaptionsstärke ε^t muss ausgehend von einem großen Wert im Laufe des Verfahrens auf einen kleinen Restwert sinken.

In dem dargestellten Lernprozess werden t_max Präsentationen durchgeführt, wonach die SOM in die Anwendungsphase überführt werden kann, in der Stimuli präsentiert werden, die in der Lernmenge nicht vorkamen. Ein solcher Stimulus wird dem Gewinnerneuron zugeordnet, dessen Gewichtsvektor die geringste Distanz von dem Stimulusvektor besitzt, sodass dem Stimulus über den Umweg des Gewichtsvektors ein Neuron und eine Position auf der Neuronenkarte zugeordnet werden kann. Auf diese Weise wird der neue Stimulus automatisch klassifiziert und visualisiert.

Varianten der SOM

Es wurden eine Vielzahl von Varianten und Erweiterungen zu dem ursprünglichen Modell von Kohonen entwickelt, u. a.:

Kontext-SOM (K-SOM)
Temporäre SOM (T-SOM)
Motorische SOM (M-SOM)
Neuronen-Gas (NG-SOM)
Wachsende Zellstrukturen (GCS-SOM)
Wachsende Gitterstruktur (GG-SOM)
Wachsende hierarchische SOM (GH-SOM)
Wachsendes Neuronen-Gas (GNG-SOM)
Parametrische SOM (P-SOM)
Hyperbolische SOM (H-SOM)
Interpolierende SOM (I-SOM)
Local-Weighted-Regression-SOM (LWR-SOM)
Selektive-Aufmerksamkeits-SOM (SA-SOM)
Gelernte Erwartungen in GNG-SOMs (LE-GNG-SOM)
Fuzzy-SOM (F-SOM)
Adaptive-Subraum-SOM (AS-SOM)
Generative Topographische Karte (GTM)

Literatur

Günter Bachelier: Einführung in selbstorganisierende Karten. Tectum-Verlag, Marburg 1998, ISBN 3-8288-5017-0
Teuvo Kohonen: Self-Organizing Maps. Springer-Verlag, Berlin 1995, ISBN 3-540-58600-8
Helge Ritter, Thomas Martinetz, Klaus Schulten: Neuronale Netze. Eine Einführung in die Neuroinformatik selbstorganisierender Netzwerke. Addison-Wesley, Bonn 1991, ISBN 3-89319-131-3

Weblinks

Commons: Selbstorganisierende Karte – Sammlung von Bildern, Videos und Audiodateien

DemoGNG.js JavaScript Simulator für SOMs und andere Netzwerkmodelle (Neural Gas, Growing Neural Gas, Growing Grid etc.)
ANNetGPGPU: C++ Library mit einer Implementierung für SOMs auf GPUs und CPUs und Python Interface
SOM-Research an der Helsinki University of Technology (Teuvo Kohonen)
Über SOM in der comp.ai.neural-nets FAQ
Java SOMToolbox: Open-Source-Anwendung zum Erstellen, Analysieren und Interagieren mit Selbstorganisierenden Karten, entwickelt an der Technischen Universität Wien.
Ultsch Marburg: Datenbionik – Datenvisualisierung und Data-Mining mit Emergenten SOM.
MusicMiner: Visualisierung von Musiksammlungen ESOM
GNOD, The Global Network of Dreams, ein Kohonen-Netz zur Bestimmung von Ähnlichkeiten von Musik, Film und Buchautoren
Demonstrationsbeispiel: HTW Dresden – ein SOM fängt einen Ball
Viscovery SOMine: SOM Technologie Tool von Viscovery
Neural Networks with Java

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.