Mustererkennung
Mustererkennung (Pattern Recognition) ist die Fähigkeit, in einer Menge von Daten Regelmäßigkeiten, Wiederholungen, Ähnlichkeiten oder Gesetzmäßigkeiten zu erkennen. Dieses Leistungsmerkmal höherer kognitiver Systeme wird für die menschliche Wahrnehmung von Kognitionswissenschaften wie der Wahrnehmungspsychologie erforscht, für Maschinen hingegen von der Informatik.
Typische Beispiele für die zahllosen Anwendungsgebiete sind Spracherkennung, Texterkennung und Gesichtserkennung, Aufgaben, die die menschliche Wahrnehmung andauernd und offensichtlich mühelos erledigt. Die elementare Fähigkeit der Klassifizierung ist jedoch auch der Grundstein von Begriffsbildung, Abstraktion und (induktivem) Denken und damit letztlich von Intelligenz, sodass die Mustererkennung auch für allgemeinere Gebiete wie die Künstliche Intelligenz oder das Data-Mining von zentraler Bedeutung ist.
Mustererkennung beim Menschen
Diese Fähigkeit bringt Ordnung in den zunächst chaotischen Strom der Sinneswahrnehmungen. Mit Abstand am besten untersucht wurde die Mustererkennung bei der visuellen Wahrnehmung. Ihre wichtigste Aufgabe ist die Identifikation (und anschließende Klassifizierung) von Objekten der Außenwelt (s. Objekterkennung).[1]
In der Wahrnehmungspsychologie unterscheidet man zwei Hauptansätze zur Erklärung der Mustererkennung: die „Schablonentheorien“ (template theories) und die „Merkmalstheorien“ (feature theories). Die Schablonentheorien gehen davon aus, dass wahrgenommene Objekte mit bereits im Langzeitgedächtnis abgelegten Objekten verglichen werden, während die Merkmalstheorien auf der Annahme beruhen, dass wahrgenommene Objekte analysiert und anhand ihrer „Bauelemente“ identifiziert werden. Zwei der umfangreichsten Merkmalstheorien sind die „Computational Theory“ von David Marr und die Theorie der geometrischen Elemente („Geons“) von Irving Biederman.
Mustererkennung in der Informatik
Die Informatik untersucht Verfahren, die gemessene Signale automatisch in Kategorien einordnen. Zentraler Punkt ist dabei das Erkennen von Mustern, den Merkmalen, die allen Dingen einer Kategorie gemeinsam sind und sie vom Inhalt anderer Kategorien unterscheiden. Mustererkennungsverfahren befähigen Computer, Roboter und andere Maschinen, statt präziser Eingaben auch die weniger exakten Signale einer natürlichen Umgebung zu verarbeiten.
Erste systematische Untersuchungsansätze der Mustererkennung kamen Mitte der 1950er Jahre mit dem Wunsch auf, Postzustellungen maschinell statt von Hand zu sortieren. Im Laufe der Zeit kristallisierten sich mit syntaktischer, statistischer und struktureller Mustererkennung die drei heutigen Gruppen von Mustererkennungsverfahren heraus. Als Durchbrüche wurden die Nutzbarmachung von Support Vector Machines und künstlichen neuronalen Netzen in den späten 1980er Jahren empfunden. Obwohl viele der heutigen Standardverfahren schon sehr früh entdeckt wurden, wurden sie erst nach erheblichen methodischen Verfeinerungen und der generellen Leistungssteigerung handelsüblicher Computer alltagstauglich.
Ansätze
Man unterscheidet heute drei prinzipielle Ansätze der Mustererkennung: Syntaktische, statistische und strukturelle Mustererkennung. Obwohl sie auf unterschiedlichen Ideen beruhen, erkennt man bei genauerer Betrachtung Gemeinsamkeiten, die so weit gehen, dass ein Verfahren der einen Gruppe ohne nennenswerten Aufwand in ein Verfahren der anderen Gruppe überführt werden kann. Von den drei Ansätzen ist die syntaktische Mustererkennung die älteste, die statistische die meistgenutzte und die strukturelle die für die Zukunft aussichtsreichste.
Syntaktisch
Ziel der syntaktischen Mustererkennung ist es, Dinge so durch Folgen von Symbolen zu beschreiben, dass Objekte der gleichen Kategorie dieselben Beschreibungen aufweisen. Möchte man etwa Äpfel von Bananen trennen, so könnte man Symbole für rot (R) und gelb (G) sowie für länglich (L) und kugelförmig (K) einführen; alle Äpfel würden dann durch die Symbolfolge RK und alle Bananen durch das Wort GL beschrieben. Das Problem der Mustererkennung stellt sich in diesem Fall als Suche nach einer formalen Grammatik dar, also nach einer Menge von Symbolen und Regeln zum Zusammenfügen derselben. Da für gewöhnlich eine klare Zuordnung zwischen Merkmal und Symbol nicht ohne weiteres möglich ist, kommen hier Methoden der Wahrscheinlichkeitsrechnung zum Einsatz. So kommen beispielsweise Farben in unzähligen Abstufungen vor, man muss jedoch eine präzise Unterscheidung zwischen rot und gelb vornehmen. Bei komplexen Sachverhalten wird damit das eigentliche Problem nur hinausgezögert statt gelöst, weshalb dieser Ansatz nur noch wenig Beachtung findet und nur bei sehr klaren Aufgabenstellungen zum Einsatz kommt.
Statistisch
In diesen Bereich fällt der größte Teil der heutigen Standardmethoden, insbesondere die oben erwähnten Support Vector Machines und künstlichen neuronalen Netze. Ziel ist es hier, zu einem Objekt die Wahrscheinlichkeit zu bestimmen, dass es zur einen oder anderen Kategorie gehört und es letztlich in die Kategorie mit der höchsten Wahrscheinlichkeit einzusortieren. Statt Merkmale nach vorgefertigten Regeln auszuwerten, werden sie hier einfach als Zahlenwerte gemessen und in einem sogenannten Merkmalsvektor zusammengefasst. Eine mathematische Funktion ordnet dann jedem denkbaren Merkmalsvektor eindeutig eine Kategorie zu. Die große Stärke dieser Verfahren liegt darin, dass sie auf nahezu alle Sachgebiete angewandt werden können und keine tiefergehende Kenntnis der Zusammenhänge vonnöten ist.
Strukturell
Die strukturelle Mustererkennung verbindet verschiedene syntaktische und/oder statistische Verfahren zu einem einzigen neuen Verfahren. Ein typisches Beispiel ist die Gesichtserkennung, bei der für verschiedene Gesichtsteile wie Auge und Nase unterschiedliche Klassifikationsverfahren eingesetzt werden, die jeweils nur aussagen, ob der gesuchte Körperteil vorliegt oder nicht. Übergeordnete strukturelle Verfahren wie etwa Bayes’sche Netze führen diese Einzelergebnisse zusammen und berechnen daraus das Gesamtergebnis, die Kategoriezugehörigkeit. Die grundlegende Merkmalserkennung wird dabei allgemeinen statistischen Verfahren überlassen, während übergeordnete Inferenzverfahren Spezialwissen über das Sachgebiet einbringen. Strukturelle Verfahren kommen besonders bei sehr komplexen Sachverhalten wie der Computer-assisted Detection, der computergestützten ärztlichen Diagnosestellung, zum Einsatz.
Teilschritte der Mustererkennung
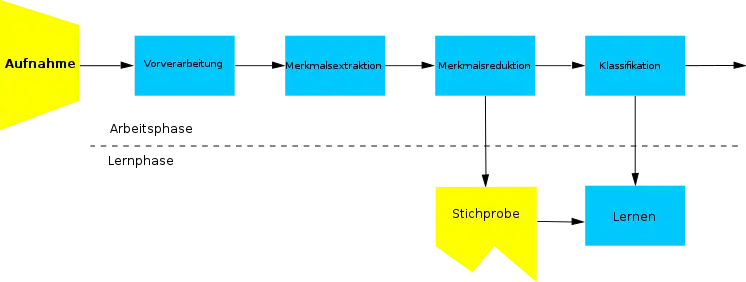
Ein Mustererkennungsprozess lässt sich in mehrere Teilschritte zerlegen, bei denen am Anfang die Erfassung und am Ende eine ermittelte Klasseneinteilung steht. Bei der Erfassung werden Daten oder Signale mittels Sensoren aufgenommen und digitalisiert. Aus den meist analogen Signalen werden Muster gewonnen, die sich mathematisch in Vektoren, sogenannten Merkmalsvektoren, und Matrizen darstellen lassen. Zur Datenreduktion und zur Verbesserung der Qualität findet eine Vorverarbeitung statt. Durch Extraktion von Merkmalen werden die Muster bei Merkmalsgewinnung anschließend in einen Merkmalsraum transformiert. Die Dimension des Merkmalsraums, in dem die Muster nun als Punkte repräsentiert sind, wird bei der Merkmalsreduktion auf die wesentlichen Merkmale beschränkt. Der abschließende Kernschritt ist die Klassifikation durch einen Klassifikator, der die Merkmale verschiedenen Klassen zuordnet. Das Klassifikationsverfahren kann auf einem Lernvorgang mit Hilfe einer Stichprobe basieren.
Erfassung
Siehe auch: Signalverarbeitung, Messung, Digitalisierung und Messtechnik
Vorverarbeitung
Um Muster besser erkennen zu können, findet in der Regel eine Vorverarbeitung statt. Die Entfernung bzw. Verringerung unerwünschter oder irrelevanter Signalbestandteile führt nicht zu einer Reduktion der zu verarbeitenden Daten, dies geschieht erst bei der Merkmalsgewinnung. Mögliche Verfahren der Vorverarbeitung sind unter anderem die Signalmittelung, Anwendung eines Schwellenwertes und Normierung. Gewünschte Ergebnisse der Vorverarbeitung sind die Verringerung von Rauschen und die Abbildung auf einen einheitlichen Wertebereich.
Merkmalsgewinnung
Nach der Verbesserung des Musters durch Vorverarbeitung lassen sich aus seinem Signal verschiedene Merkmale gewinnen. Dies geschieht in der Regel empirisch nach durch Intuition und Erfahrung gewonnenen Verfahren, da es wenige rein analytische Verfahren (z. B. die Automatische Merkmalsynthese) gibt. Welche Merkmale wesentlich sind, hängt von der jeweiligen Anwendung ab. Merkmale können aus Symbolen beziehungsweise Symbolketten bestehen oder mit statistischen Verfahren aus verschiedenen Skalenniveaus gewonnen werden. Bei den numerischen Verfahren unterscheidet man Verfahren im Originalbereich und Verfahren im Spektralbereich. Mögliche Merkmale sind beispielsweise
- Kennzahlen der Verteilungsfunktion
- Momente wie Erwartungswert und Varianz
- Korrelation und Faltung
Mittels Transformationen wie der diskreten Fourier-Transformation (DFT) und diskreten Kosinustransformation (DCT) können die ursprünglichen Signalwerte in einen handlicheren Merkmalsraum gebracht werden. Die Grenzen zwischen Verfahren der Merkmalsgewinnung und Merkmalsreduktion sind fließend. Da es wünschenswert ist, möglichst wenige aber dafür umso aussagekräftigere Merkmale zu gewinnen, können Beziehungen wie die Kovarianz und der Korrelationskoeffizient zwischen mehreren Merkmalen berücksichtigt werden. Mit der Karhunen-Loève-Transformation (Hauptachsentransformation) lassen sich Merkmale dekorrelieren.
Merkmalsreduktion
Zur Reduktion der Merkmale auf die für die Klassifikation wesentlichen wird geprüft, welche Merkmale für die Klassentrennung relevant sind und welche weggelassen werden können. Verfahren der Merkmalsreduktion sind die Varianzanalyse, bei der geprüft wird, ob ein oder mehrere Merkmale Trennfähigkeit besitzen, und die Diskriminanzanalyse, bei der durch Kombination von elementaren Merkmalen eine möglichst geringe Zahl trennfähiger nichtelementarer Merkmale gebildet wird.
Klassifizierung
Der letzte und wesentliche Schritt der Mustererkennung ist die Klassifizierung der Merkmale in Klassen. Dazu existieren verschiedene Klassifikationsverfahren.
Lebewesen benutzen zur Mustererkennung in den Signalen unserer Sinne meist Neuronale Netze. Diese Herangehensweise wird in der Bionik analysiert und imitiert. Die Neuroinformatik hat gezeigt, dass durch künstliche neuronale Netze Lernen und Erkennung komplexer Muster möglich sind, auch ohne dass vorher eine Regelabstraktion in oben gezeigter Art erfolgt.
Im Anschluss an die Klassifizierung des Musters kann versucht werden, das Muster zu interpretieren. Dies ist Gegenstand der Musteranalyse. In der Bildverarbeitung kann auf die Klassifizierung von Bildern eine sogenannte Bilderkennung folgen, also die bloße Erkennung von Objekten in einem Bild ohne Interpretation oder Analyse von Zusammenhängen zwischen diesen Objekten.
Siehe auch
Literatur
- Richard O. Duda, Peter E. Hart, David G. Stork: Pattern classification. Wiley, New York 2001, ISBN 0-471-05669-3.
- J. Schuermann: Pattern Classification – A Unified View of Statistical and Neural Approaches. Wiley, New York 1996, ISBN 0-471-13534-8.
- K. Fukunaga: Statistical Pattern Recognition. Academic Press, New York 1991, ISBN 0-12-269851-7.
- M. Eysenck, M. Keane: Cognitive Psychology. Psychology Press, Hove, 2000.
- H. Niemann: Klassifikation von Mustern. Springer, Berlin 1983, ISBN 3-540-12642-2. (online).
- Christopher M. Bishop: Pattern Recognition and Machine Learning. Springer, Berlin 2006, ISBN 0-387-31073-8. (online).
- Monique Pavel: Fundamentals of pattern recognition. 2. Auflage. Dekker, New York 1993, ISBN 0-824-78883-4.
Weblinks
Einzelnachweise
- E. Bruce Goldstein: Wahrnehmungspsychologie. Spektrum Akademischer Verlag, Heidelberg 2002, ISBN 3-8274-1083-5