Chomsky-Hierarchie

Chomsky-Hierarchie, gelegentlich Chomsky-Schützenberger-Hierarchie (benannt nach dem Linguisten Noam Chomsky und dem Mathematiker Marcel Schützenberger), ist ein Begriff aus der Theoretischen Informatik. Sie ist eine Hierarchie von Klassen formaler Grammatiken, die formale Sprachen erzeugen, und wurde 1956 erstmals von Noam Chomsky beschrieben. Die Hierarchiestufen unterscheiden sich darin, wie rigide die Einschränkungen für die Form zulässiger Produktionsregeln auf der jeweiligen Stufe sind; bei Typ-0-Grammatiken sind sie uneingeschränkt, bei höheren Stufen fortschreitend stärker beschränkt.

Grammatiken niedrigeren Typs sind erzeugungsmächtiger als die höherer Typen. Eine Sprache, die von einer Grammatik des Typs k erzeugt wird, heißt eine Sprache des Typs k. Neben die Chomsky-Hierarchie der Grammatiken tritt in diesem Sinne eine Chomsky-Hierarchie der Sprachen.

Hintergründe

Formale Sprachen haben den Vorzug, mathematisch exakt analysiert werden zu können. Formalen Sprachen liegt ein vorgegebenes Alphabet (ein Zeichenvorrat) zugrunde, das häufig mit $\Sigma$ bezeichnet wird. Beliebig lange, endliche Folgen von Elementen des Alphabets werden als Wörter über dem Alphabet bezeichnet. Mengen solcher Wörter sind schließlich formale Sprachen. Die umfassendste formale Sprache über einem vorgegebenen Alphabet $\Sigma$ ist unendlich groß; sie enthält sämtliche Wörter, die durch beliebiges Zusammenfügen von Zeichen des Alphabets gebildet werden können. Sie lässt sich durch die Kleenesche Hülle des Alphabets beschreiben, also $\Sigma ^{*}$ . Die kleinste formale Sprache enthält gar keine Wörter. Andere formale Sprachen bestehen nur aus wenigen Wörtern und lassen sich somit als endliche Menge notieren; beispielsweise für das Alphabet $\textstyle \Sigma =\{a,b\}$ die Sprache aller Wörter der Länge zwei: $\textstyle L=\{aa,ab,ba,bb\}$ .

Unendliche Sprachen lassen sich begreiflicherweise nicht durch Aufzählen notieren. Um sie exakt zu beschreiben, ist ein Konzept nötig, das auch unendliche Mengen definieren kann. Hierzu werden im Rahmen der formalen Sprachen vor allem Erzeugungsverfahren benutzt.

Geht man von einem vorhandenen Wort über einem Alphabet aus, lassen sich durch Semi-Thue-Systeme Wortmengen spezifizieren, die sich durch beliebig wiederholtes Anwenden von Ersetzungsregeln ergeben. Ersetzungsregeln der Form $\alpha \rightarrow \beta$ schreiben vor, dass in einem Wort, das ein Segment $\alpha$ enthält, dieses Segment durch $\beta$ ersetzt wird. Semi-Thue-Systeme geben daher eine Ableitungsrelation zwischen Wörtern formaler Sprachen an: Zwei Wörter stehen in Relation, wenn das eine Wort durch eine Ersetzungsregel vom anderen Wort abgeleitet werden kann.

Zur Beschreibung von formalen Sprachen eignen sich formale Grammatiken, ein gegenüber Semi-Thue-Systemen erweitertes und mächtigeres Konzept. Sie unterscheiden sich von Semi-Thue-Systemen darin, dass sie sogenannte Terminalsymbole und Nichtterminalsymbole kennen. Terminalsymbole einer Grammatik sind gerade alle Zeichen ihres Zeichensatzes $\Sigma$ . Die erste anwendbare Regel geht immer von einem nichtterminalen Startsymbol aus, und das Ergebnis eines Ersetzungsvorgangs gilt nur dann als Wort ihrer formalen Sprache, wenn es keine Nichtterminalsymbole enthält.

Das folgende Beispiel beschreibt eine Sprache, mit der sich beliebig lange Summen der Ziffern 1, 2 und 3 ausdrücken lassen. Das dafür angemessene Alphabet ist $\Sigma =\{+,1,2,3\}$ . Die entsprechenden Terminalsymbole sind unterstrichen dargestellt, Nicht-Terminale kursiv. Die folgenden Zeilen stellen die Regeln dar.

{\begin{aligned}{\mathit {Summe}}&\rightarrow {\mathit {Ziffer}}\\{\mathit {Summe}}&\rightarrow {\mathit {Summe}}\ {\underline {+}}\ {\mathit {Ziffer}}\\{\mathit {Ziffer}}&\rightarrow {\underline {1}}\\{\mathit {Ziffer}}&\rightarrow {\underline {2}}\\{\mathit {Ziffer}}&\rightarrow {\underline {3}}\\\end{aligned}}

Das Startsymbol dieser Sprache ist Summe. Davon ausgehend kann man nun beliebige Regeln nacheinander anwenden, um einen gültigen Ausdruck zu erzeugen:

{\begin{aligned}&{\mathit {Summe}}&\quad &{\text{(Startsymbol)}}\\&{\mathit {Summe}}\ {\underline {+}}\ {\mathit {Ziffer}}&&{\text{(mit zweiter Regel)}}\\&{\mathit {Ziffer}}\ {\underline {+}}\ {\mathit {Ziffer}}&&{\text{(mit erster Regel)}}\\&{\underline {1\ +}}\ {\mathit {Ziffer}}&&{\text{(mit 1. Ziffern-Regel)}}\\&{\underline {1+2}}&&{\text{(mit 2. Ziffern-Regel)}}\\\end{aligned}}

Nicht alle unendlichen Sprachen lassen sich als formale Sprachen mit diesem Erzeugungsprinzip beschreiben, es ist aber kein tauglicheres Konzept bekannt. Ein anderer gängiger Formalismus zur Beschreibung von Sprachen sind Automatenmodelle, vor allem Turingmaschinen. Uneingeschränkte formale Grammatiken und Turingmaschinen sind bei der Beschreibung von formalen Sprachen gleichmächtig, d. h. zu jeder von einer formalen Grammatik erzeugten Sprache gibt es eine Turingmaschine, die genau diese akzeptiert, und umgekehrt.

Ebenso wie verschiedene Automatenmodelle definiert wurden, definierte Chomsky in seiner Arbeit verschiedene Grammatiktypen. Durch drei fortlaufend schärfere Einschränkungen an die jeweils darin zulässigen Ersetzungsregeln stellte er eine Hierarchie aus vier Klassen von formalen Grammatiken auf, wodurch die weniger eingeschränkten Klassen die stärker regulierten Klassen jeweils echt umfassen. Das Gleiche gilt für die von den jeweiligen Grammatikklassen beschriebenen Sprachklassen: auch sie bilden eine Hierarchie.

Sprachen eingeschränkteren Grammatiktyps sind üblicherweise einfacher algorithmisch zu verarbeiten – um den Preis, weniger ausdrucksmächtig zu sein. Reguläre Ausdrücke, mit denen man etwa Muster für die Suche in Texten definiert, entsprechen zum Beispiel den sehr eingeschränkten Chomsky-Grammatiken des Typs 3 (reguläre Grammatiken) und solche Textsuchen sind effektiv und schnell. Dagegen taugen Grammatiken des Typs 3 wegen ihrer Einfachheit nicht zur Beschreibung von Programmiersprachen, für die man meist weniger eingeschränkte Typ-2-Grammatiken benutzt.

Die Hierarchie

Die Chomsky-Hierarchie umfasst vier Typen formaler Grammatiken, gezählt von 0 bis 3. Typ 0 umfasst alle formalen Grammatiken überhaupt, also ohne Einschränkung an die Gestalt zulässiger Erzeugungsregeln. Grammatiken des Typs 1 bis Typ 3 sind dann zunehmend stärker eingeschränkt. Allein nach Definition ist eine Grammatik vom Typ 1 auch vom Typ 0, eine Grammatik vom Typ 2 auch vom Typ 1, eine Grammatik vom Typ 3 auch vom Typ 2; die Umkehrungen gelten nicht. Deshalb bilden diese Klassen eine echte Hierarchie. Bei den entsprechenden Sprachklassen zeigen Gegenbeispiele, dass ebenfalls die Umkehrungen nicht gelten, weshalb auch sie eine echte Hierarchie bilden.

Chomsky forderte für Typ-1-, Typ-2- und Typ-3-Grammatiken, dass die rechte Seite von Produktionsregeln nicht kürzer als die linke Seite sein darf, was auch das leere Wort auf jeder rechten Seite einer Produktionsregel ausschließt. Heute ist man oft weniger restriktiv; die Definitionen sind oft so gefasst, dass die Hierarchie der Sprachen nicht gestört wird, sie es aber auch Grammatiken des Typs 1 (kontextsensitive Grammatiken) durch eine Ausnahmeregel erlauben, das leere Wort zu erzeugen, und den Typen 2 (kontextfreien Grammatiken) und 3 (regulären Grammatiken) sogar ohne Einschränkung das leere Wort als rechte Seite von Ersetzungsregeln gestatten.

Typ-0-Grammatik (allgemeine Chomsky-Grammatik oder Phrasenstrukturgrammatik)

Definition

Typ-0-Grammatiken werden auch unbeschränkte Grammatiken genannt. Es handelt sich dabei um die Klasse aller formalen Grammatiken der Form $G=$ $(V,T,P,S)$ , wobei $V=T\cup N$ ein Vokabular ist, bestehend aus der disjunkten Vereinigung eines endlichen Alphabets $T$ (Terminalsymbole) und einer Menge von Nichtterminalen (Variablen) $N$ .[1] Das ausgezeichnete Symbol $S\in N$ wird als Startsymbol bezeichnet und $P$ ist eine Menge von Produktionsregeln $P\subset$ $(V^{*}\setminus {T}^{*})$ $\times$ $V^{*}$ $=$ $V^{*}NV^{*}$ $\times$ $V^{*}$ , d. h. auf der linken Seite jeder Produktionsregel steht wenigstens ein Nicht-Terminalsymbol. Für einzelne Regeln schreibt man anstelle von $(\alpha ,\beta )\in P$ meistens $\alpha \rightarrow \beta$ , für die Menge der Regeln mit $\alpha$ auf der linken Seite $\{(\alpha ,\beta _{1}),...(\alpha ,\beta _{n})\}\subseteq P$ auch $\alpha \rightarrow \beta _{1}|...|\beta _{n}$ .

Um die Zugehörigkeit zur Klasse der Typ-0-Grammatiken auszudrücken, schreibt man $G\in {\mbox{Typ}}_{0}.$

Von Typ-0-Grammatiken erzeugte Sprachen

Jede Typ-0-Grammatik erzeugt eine Sprache, die von einer Turingmaschine akzeptiert werden kann, und umgekehrt existiert für jede Sprache, die von einer Turingmaschine akzeptiert werden kann, eine Typ-0-Grammatik, die diese Sprache erzeugt. Diese Sprachen sind auch bekannt als die rekursiv aufzählbaren Sprachen (oft auch semi-entscheidbare Sprachen genannt), d. h. die zugehörige Turingmaschine akzeptiert jedes Wort, das in der Sprache liegt. Bei einem Wort, das nicht in der Sprache liegt, kann es sein, dass die Turingmaschine nicht terminiert, d. h. keinerlei Auskunft über die Zugehörigkeit des Worts zur Sprache liefert.

Man beachte, dass sich diese Menge von Sprachen von der Menge der rekursiven Sprachen (oft auch entscheidbare Sprachen genannt) unterscheidet, welche durch Turingmaschinen entschieden werden können.

Typ-1-Grammatik (kontextsensitive Grammatik)

Definition

Typ-1-Grammatiken werden auch kontextsensitive Grammatiken genannt. Es handelt sich dabei um Typ-0-Grammatiken, bei denen alle Produktionsregeln die Form $\alpha A\beta \rightarrow \alpha \gamma \beta$ oder $S\rightarrow \varepsilon$ haben, wobei $A$ ein Nichtterminal und $\alpha ,\gamma ,\beta$ Wörter bestehend aus Terminalen ( $T$ ) und Nichtterminalen ( $N$ ) sind. $\varepsilon$ bezeichnet das leere Wort. Die Wörter $\alpha$ und $\beta$ können leer sein, aber $\gamma$ muss mindestens ein Symbol (also ein Terminal oder ein Nichtterminal) enthalten. Diese Eigenschaft wird Längenbeschränktheit genannt.

Als einzige Ausnahme von dieser Forderung lässt man $S\rightarrow \varepsilon$ zu, wenn das Startsymbol nirgends auf der rechten Seite einer Produktion auftritt. Damit erreicht man, dass die kontextsensitiven Sprachen auch das oft erwünschte leere Wort enthalten können, das dann aber immer nur in einer einschrittigen Ableitung aus dem Startsymbol selbst entsteht, und ohne für alle anderen Ableitungen die Eigenschaft zu stören, dass in jedem Teilschritt die Satzform länger wird oder gleich lang bleibt.

Ist eine Grammatik $G$ kontextsensitiv, so schreibt man $G\in {\mbox{Typ}}_{1}$ .

Anders als bei kontextfreien Grammatiken können auf der linken Seite der Produktionen kontextsensitiver Grammatiken durchaus statt einzelner Symbole ganze Symbolfolgen stehen, sofern sie mindestens ein Nichtterminalsymbol enthalten.

Von Typ-1-Grammatiken erzeugte Sprachen

Die kontextsensitiven Grammatiken erzeugen genau die kontextsensitiven Sprachen. Das heißt: Jede Typ-1-Grammatik erzeugt eine kontextsensitive Sprache und zu jeder kontextsensitiven Sprache existiert eine Typ-1-Grammatik, die diese erzeugt.

Die kontextsensitiven Sprachen sind genau die Sprachen, die von einer nichtdeterministischen, linear beschränkten Turingmaschine erkannt werden können; das heißt von einer nichtdeterministischen Turingmaschine, deren Band linear durch die Länge der Eingabe beschränkt ist (das bedeutet, es gibt eine konstante Zahl $a$ , sodass das Band der Turingmaschine höchstens $a\cdot x$ Felder besitzt, wobei $x$ die Länge des Eingabewortes ist).

Monotone Grammatiken

Einige Autoren bezeichnen eine Grammatik schon dann als kontextsensitiv, wenn bis auf die Ausnahme $S\rightarrow \varepsilon$ (s. o.) alle Produktionsregeln $w_{1}\rightarrow w_{2}$ nur die Bedingung $\left|w_{1}\right|\leq \left|w_{2}\right|$ erfüllen, d. h., dass die rechte Seite einer solchen Produktion nicht kürzer als deren linke Seite ist. Häufiger findet man dafür jedoch den Begriff der monotonen Grammatik oder der nichtverkürzenden Grammatik.

Es erweist sich, dass die monotonen Grammatiken genau wieder die kontextsensitiven Sprachen erzeugen, weshalb die beiden Klassen von Grammatiken als äquivalent betrachtet werden und manche Autoren nur die eine oder die andere Grammatikklasse überhaupt behandeln. Aber nicht jede monotone Ersetzungsregel ist auch eine kontextsensitive, deshalb ist auch nicht jede monotone Grammatik eine kontextsensitive.

Typ-2-Grammatik (kontextfreie Grammatik)

Definition

Typ-2-Grammatiken werden auch kontextfreie Grammatiken genannt. Es sind Grammatiken, für die gelten muss: $\forall (w_{1}\rightarrow w_{2})\in P:(w_{1}\in N)\land \left(w_{2}\in V^{+}\right).$ In jeder Regel der Grammatik muss also auf der linken Seite genau ein nicht-terminales Symbol stehen und auf der rechten Seite kann eine beliebige nicht-leere Folge von terminalen und nichtterminalen Symbolen aus dem gesamten Vokabular $V=N\cup T$ stehen.

Außerdem kann wie bei Typ-1-Grammatiken die Ausnahmeregel $S\rightarrow \varepsilon$ zugelassen werden, wenn $S$ auf keiner rechten Seite einer Regel vorkommt.

Man schreibt $G\in {\mbox{Typ}}_{2}.$

Kontextfreie Grammatiken werden oft so definiert, dass die rechte Seite auch leer sein darf, also $(w_{1}\rightarrow \varepsilon )\in P$ . Solche Grammatiken erfüllen nicht mehr alle Eigenschaften von Typ-2-Grammatiken und stünden nicht mehr in der von Chomsky definierten Hierarchie. Sie erfüllen aber die Bedingungen von monotonen Grammatiken.

Von Typ-2-Grammatiken erzeugte Sprachen

Kontextfreie Grammatiken (mit $\varepsilon$ -Ausnahmeregel) erzeugen genau die kontextfreien Sprachen, jede Typ-2-Grammatik erzeugt also eine kontextfreie Sprache und zu jeder kontextfreien Sprache existiert eine Typ-2-Grammatik, die diese erzeugt.

Die kontextfreien Sprachen sind genau die Sprachen, die von einem nichtdeterministischen Kellerautomaten (NPDA) erkannt werden können. Eine Teilmenge dieser Sprachen bildet die theoretische Basis für die Syntax der meisten Programmiersprachen.

Siehe auch: Backus-Naur-Form (BNF) / Erweiterte Backus-Naur-Form (EBNF): ein anderes, äquivalentes Schema der Bezeichnungsweisen.

Typ-3-Grammatik (reguläre Grammatik)

Definition

Typ-3-Grammatiken werden auch reguläre Grammatiken genannt. Es handelt sich um Typ-2-Grammatiken, bei denen auf der rechten Seite von Produktionen genau ein Terminalsymbol auftreten darf und maximal ein weiteres Nichtterminalsymbol. Die erlaubte Stellung solcher Nichtterminalsymbole muss außerdem über alle Produktionen hinweg einheitlich immer vor oder immer hinter dem Terminalsymbol sein, je nachdem spricht man auch genauer von linksregulären und rechtsregulären Grammatiken. Sie stimmen mit den links- beziehungsweise rechts-linearen Grammatiken überein, wohingegen lineare Grammatiken nicht den regulären Grammatiken entsprechen.

Für linksreguläre Typ-3-Grammatiken muss also die Bedingung erfüllt sein, dass

$\forall (w_{1}\rightarrow w_{2})\in P:(w_{1}\in N)\land$ $(w_{2}\in T\cup NT)$ .

Sie dürfen also nur linksreguläre Produktionen (Nichtterminalsymbol auf der rechten Seite in Vorderstellung) enthalten.

Üblicherweise gestattet man für reguläre Grammatiken, wie auch für kontextfreie Grammatiken Regeln mit leerer rechter Seite, also $(w_{1}\rightarrow \varepsilon )\in P$ .

Rechtsreguläre Grammatiken erfüllen dagegen die analoge Bedingung

$\forall (w_{1}\rightarrow w_{2})\in P:(w_{1}\in N)\land$ $(w_{2}\in T\cup TN\cup \{\varepsilon \})$ .

Diese enthalten also nur rechtsreguläre Produktionen (Nichtterminalsymbol auf der rechten Seite allenfalls in Hinterstellung). Diese Bedingung drückt auch schon die Erlaubnis leerer rechter Seiten aus.

Linksreguläre und rechtsreguläre Grammatiken erzeugen genau dieselbe Sprachklasse, es gibt also zu jeder linksregulären Grammatik auch eine rechtsreguläre, die dieselbe Sprache erzeugt, und umgekehrt.

Man beachte, dass beim Auftreten von linksregulären und rechtsregulären Produktionen in ein und derselben Chomsky-Grammatik diese nicht regulär ist. Die Grammatiken mit sowohl linksregulären als auch rechtsregulären Produktionen erzeugen nämlich eine echt größere Sprachklasse.

Manche Autoren erlauben in den Definitionen für reguläre / linksreguläre / rechtsreguläre Grammatiken überall dort, wo hier in Produktionen nur ein einzelnes Nichtterminalzeichen stehen darf, auch eine beliebige nichtleere terminale Zeichenkette. An der Erzeugungsmächtigkeit der Klassen ändert sich dadurch nichts.

Man schreibt $G\in {\mbox{Typ}}_{3}$ für reguläre Grammatiken $G$ .

Von Typ-3-Grammatiken erzeugte Sprachen

Reguläre Grammatiken erzeugen genau die regulären Sprachen, das heißt, jede Typ-3-Grammatik erzeugt eine reguläre Sprache und zu jeder regulären Sprache existiert eine Typ-3-Grammatik, die diese erzeugt.

Reguläre Sprachen können alternativ auch durch reguläre Ausdrücke beschrieben werden und die regulären Sprachen sind genau die Sprachen, die von endlichen Automaten erkannt werden können. Sie werden häufig genutzt, um Suchmuster oder die lexikalische Struktur von Programmiersprachen zu definieren.

Übersicht

Die folgende Tabelle führt für die vier Grammatiktypen auf, welche Form ihre Regeln haben, welchen Namen die erzeugten Sprachen haben und welche Automatentypen diese Sprachen erkennen, also das Wortproblem zumindest semi-entscheiden (Wort in Sprache: Maschine hält in akzeptierendem Endzustand, Wort nicht in Sprache: Maschine hält nie oder hält in nicht akzeptierendem Zustand → sicher hält die Maschine also nur, wenn das Wort in der Sprache ist). Da in der Chomsky-Hierarchie für die Sprachmengen aber eine echte Teilmengenbeziehung gilt (siehe nächster Abschnitt) entscheiden z. B. Turingmaschinen selbstverständlich ebenfalls das Wortproblem für Sprachen vom Typ 1 bis 3. (entscheiden heißt: Wort in Sprache: Maschine hält in akzeptierendem Endzustand, Wort nicht in Sprache: Maschine hält in nicht akzeptierendem Zustand → irgendwann hält die Maschine und das Problem (Wort in Sprache?) ist entschieden) Außerdem wird vermerkt, gegenüber welchen Operationen die erzeugten Sprachen abgeschlossen sind.

Grammatik	Regeln	Sprachen	Entscheidbarkeit	Automaten	Abgeschlossenheit[2]	Zeitabschätzung
Typ-0 Beliebige formale Grammatik	$\alpha \rightarrow \beta$ $\alpha \in V^{}\setminus T^{},\beta \in V^{\ast }$	rekursiv aufzählbar (nicht „nur“ rekursiv, die wären entscheidbar!)	–	Turingmaschine (egal ob deterministisch oder nicht-deterministisch)	$\circ ,\cap ,\cup ,\ast$	unbeschränkt
Typ-1 Kontextsensitive Grammatik	$\alpha A\beta \rightarrow \alpha \gamma \beta$ $A\in N,\alpha ,\beta \in V^{\ast },\gamma \in V^{+}\;$ $S\rightarrow \varepsilon$ ist erlaubt, wenn es keine Regel $\alpha \rightarrow \beta S\gamma$ in $P$ gibt.	kontextsensitiv	Wortproblem	linear platzbeschränkte nichtdeterministische Turingmaschine	$\complement ,\circ ,\cap ,\cup ,\ast$	$O(2^{n})$
Typ-2 Kontextfreie Grammatik	$A\rightarrow \gamma$ $A\in N,\gamma \in V^{\ast }$	kontextfrei	Wortproblem, Leerheitsproblem, Endlichkeitsproblem	nichtdeterministischer Kellerautomat	$\circ ,\cup ,\ast$	$O(n^{3})$
Typ-3 Reguläre Grammatik	$A\rightarrow aB$ (rechtsregulär) oder $A\rightarrow Ba$ (linksregulär) $A\rightarrow a$ $A\rightarrow \varepsilon$ $A,B\in N,a\in T$ Nur links- oder nur rechtsreguläre Produktionen	regulär	Wortproblem, Leerheitsproblem, Endlichkeitsproblem, Äquivalenzproblem	Endlicher Automat (egal ob deterministisch oder nicht-deterministisch)	$\complement ,\circ ,\cap ,\cup ,\ast$	$O(n)$

Legende für die Spalte Regeln

$T$ … endliches Alphabet (Menge der Terminalsymbole, oft auch mit $\Sigma$ bezeichnet, das aber auch $V\cup N$ bedeuten kann)
$N$ … die davon disjunkte Menge der Nichtterminalsymbole (gelegentlich auch Variablen genannt und mit $V$ bezeichnet, statt $V:=N\cup T$ … gesamtes Vokabular)
$S\in N$ … Startsymbol
$\varepsilon$ … leeres Wort (oft auch mit $\lambda$ bezeichnet)
$P$ … Menge von Produktionsregeln (als Teilmenge eines kartesischen Produkts eine Relation)
$\setminus$ … Mengen-Differenzbildung
$^{\ast }$ … Kleenescher Abschluss (Hülle), siehe Kleenesche und positive Hülle
$^{+}$ … positive Hülle, z. B. meint $\gamma \in (T\cup N)^{+}=V^{+}$ … $\gamma$ muss mindestens ein Symbol (Terminal oder ein Nichtterminal) enthalten

In der obigen Tabelle werden somit mit lateinischen Großbuchstaben Nichtterminalsymbole dargestellt, $A,B\in N$ mit lateinischen Kleinbuchstaben Terminalsymbole $a\in T$ und griechische Kleinbuchstaben werden verwendet, wenn es sich sowohl um Nichtterminal als auch um Terminalsymbole handeln kann.

Achtung: Bei $^{\ast }$ und $^{+}$ kann ein griechischer Kleinbuchstabe für Wörter aus mehreren Terminal- oder Nichtterminalsymbolen stehen!

Legende für die Spalte Abgeschlossenheit

$\complement$ … Komplementbildung
$\circ$ … Konkatenation
$\cap$ … Schnittmenge
$\cup$ … Vereinigungsmenge
$^{\ast }$ … Kleenescher Abschluss (Hülle)

Chomsky-Hierarchie für formale Sprachen

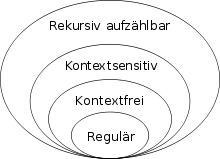
Teilmengenbeziehung der Sprachklassen in der Chomsky-Hierarchie

Eine formale Sprache ist vom Typ $i$ entsprechend der Hierarchie für Grammatiken, wenn es von einer Typ- $i$ -Grammatik erzeugt wird. Formal ausgedrückt heißt das: $L$ ist vom Typ $i\in \{0,\ldots ,3\},$ falls es eine Grammatik $G\in {\mbox{Typ}}_{i}$ mit $L=L\left(G\right)$ gibt. Man schreibt dann $L\in {\mathcal {L}}_{i}.$

In der Chomsky-Hierarchie für formale Sprachen besteht zwischen den Sprachmengen benachbarter Ebenen eine echte Teilmengenbeziehung. Jede kontextsensitive Sprache ist rekursiv aufzählbar, aber es gibt rekursiv aufzählbare Sprachen, die nicht kontextsensitiv sind. Ebenso ist jede kontextfreie Sprache auch kontextsensitiv, aber nicht umgekehrt, und jede reguläre Sprache ist kontextfrei, aber nicht jede kontextfreie Sprache ist regulär.

Formal ausgedrückt bedeutet dies für die Klassen der durch die obigen Grammatiken erzeugten Sprachen: ${\mathcal {L}}_{3}\subset {\mathcal {L}}_{2}\subset {\mathcal {L}}_{1}\subset {\mathcal {L}}_{0},$ wobei gelegentlich auch folgende Symbole verwendet werden: $\mathrm {REG} \subset \mathrm {CF} \subset \mathrm {CS} \subset \mathrm {RE.}$

Beispiele für Sprachen in den jeweiligen Differenzmengen sind:

$L_{1}=\left\{a^{n}b^{n}c^{n}\,|\,n\geq 1\right\}$ ist vom Typ 1, aber nicht vom Typ 2
$L_{2}=\left\{a^{n}b^{n}\,|\,n\geq 1\right\}$ ist vom Typ 2, aber nicht vom Typ 3

Beweise für die Nichtzugehörigkeit bestimmter Sprachen zu den Sprachklassen ${\mathcal {L}}_{2}$ und ${\mathcal {L}}_{3}$ wie hier werden oft mit dem Schleifensatz geführt.

Natürliche Sprachen

Obwohl Chomsky seine Forschungen mit dem Ziel verfolgte, eine mathematische Beschreibung der natürlichen Sprachen zu finden, ist bis heute für keine natürliche Sprache der Nachweis einer korrekten und vollständigen formalen Grammatik gelungen.[3] Das Problem besteht u. a. im Zusammenspiel der verschiedenen Grammatikteile, die jeweils einzelne sprachliche Phänomene modellieren. Aber auch beim praktischen Einsatz formaler Grammatiken in der Computerlinguistik kann es zu Mehrdeutigkeiten auf verschiedenen Ebenen der Sprachbetrachtung kommen; diese müssen (z. B. in der maschinellen Übersetzung) anhand des Kontextes aufgelöst werden.

Literatur

Noam Chomsky: Three models for the description of language. In: IRE Transactions on Information Theory. Vol.2, 1956, S. 113–124 (PDF).
Noam Chomsky: On certain formal properties of grammars. In: Information and Control. Vol.2, 1959, S. 137–167 (PDF).
Noam Chomsky, Marcel P. Schützenberger: The algebraic theory of context free languages, Computer Programming and Formal Languages. Hrsg.: P. Braffort, D. Hirschberg. North Holland, Amsterdam 1963, S. 118–161.
Peter Sander, Wolffried Stucky, Rudolf Herschel: Automaten, Sprachen, Berechenbarkeit. Teubner, Stuttgart 1992, ISBN 3-519-02937-5.

Einzelnachweise

Im Zusammenhang mit formalen Grammatiken wird hier für das ‚Zielalphabet’ der Terminalsymbole das Zeichen $T$ statt - wie sonst - $\Sigma$ verwendet. Achtung: Manche Autoren bezeichnen mit $\Sigma$ abweichend das Gesamtvokabular $N\cup T$ (hier mit $V$ bezeichnet).
Uwe Schöning: Theoretische Informatik - kurz gefasst. 5. Auflage. Spektrum Akademischer Verlag, Heidelberg 2008, ISBN 978-3-8274-1824-1, S. 81.
John Spacey: Natural Language vs. Formal Language. In: Simplicable. 12. April 2017, abgerufen am 6. September 2021 (englisch).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Im Zusammenhang mit formalen Grammatiken wird hier für das ‚Zielalphabet’ der Terminalsymbole das Zeichen $T$ statt - wie sonst - $\Sigma$ verwendet. Achtung: Manche Autoren bezeichnen mit $\Sigma$ abweichend das Gesamtvokabular $N\cup T$ (hier mit $V$ bezeichnet).

[2] Uwe Schöning: Theoretische Informatik - kurz gefasst. 5. Auflage. Spektrum Akademischer Verlag, Heidelberg 2008, ISBN 978-3-8274-1824-1, S. 81.

[3] John Spacey: Natural Language vs. Formal Language. In: Simplicable. 12. April 2017, abgerufen am 6. September 2021 (englisch).