Convolutional Neural Network

Ein Convolutional Neural Network (CNN oder ConvNet), zu Deutsch etwa „faltendes neuronales Netzwerk“, ist ein künstliches neuronales Netz. Es handelt sich um ein von biologischen Prozessen inspiriertes Konzept im Bereich des maschinellen Lernens[1]. Convolutional Neural Networks finden Anwendung in zahlreichen Technologien der künstlichen Intelligenz, vornehmlich bei der maschinellen Verarbeitung von Bild- oder Audiodaten.

Als Begründer der CNNs gilt Yann LeCun.

Aufbau

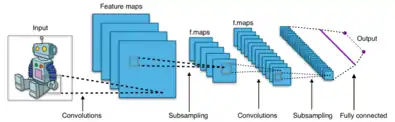
Struktur eines typischen CNNs zur Bildklassifikation. Subsampling entspricht Pooling. Dieses Netz besitzt pro Convolutional Layer mehrere Filterkernel, sodass Schichten an Feature Maps entstehen, die jeweils die gleiche Eingabe bekommen, jedoch aufgrund unterschiedlicher Gewichtsmatrizen unterschiedliche Features extrahieren.

Grundsätzlich besteht die Struktur eines klassischen Convolutional Neural Networks aus einem oder mehreren Convolutional Layer, gefolgt von einem Pooling Layer. Diese Einheit kann sich prinzipiell beliebig oft wiederholen, bei ausreichend Wiederholungen spricht man dann von Deep Convolutional Neural Networks, die in den Bereich Deep Learning fallen. Architektonisch können im Vergleich zum mehrlagigen Perzeptron drei wesentliche Unterschiede festgehalten werden (Details hierzu siehe Convolutional Layer):

2D- oder 3D-Anordnung der Neuronen
Geteilte Gewichte
Lokale Konnektivität

Convolutional Layer

In der Regel liegt die Eingabe als zwei- oder dreidimensionale Matrix (z. B. die Pixel eines Graustufen- oder Farbbildes) vor. Dementsprechend sind die Neuronen im Convolutional Layer angeordnet.

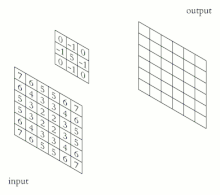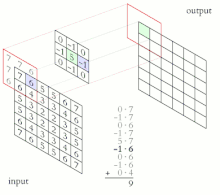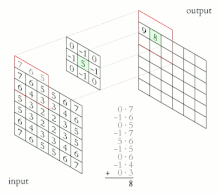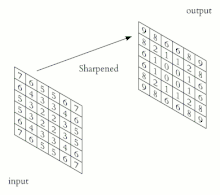
Die Aktivität jedes Neurons wird über eine diskrete Faltung (daher der Zusatz convolutional) berechnet. Dabei wird schrittweise eine vergleichsweise kleine Faltungsmatrix (Filterkernel) über die Eingabe bewegt. Die Eingabe eines Neurons im Convolutional Layer berechnet sich als inneres Produkt des Filterkernels mit dem aktuell unterliegenden Bildausschnitt. Dementsprechend reagieren benachbarte Neuronen im Convolutional Layer auf sich überlappende Bereiche (ähnliche Frequenzen in Audiosignalen oder lokale Umgebungen in Bildern).[2]

Animation einer 2D-Convolution. Die Werte im Kernel werden selbstständig erlernt. Zur Behandlung der Randregionen des Inputs existieren verschiedene Padding-Methoden.

Hervorzuheben ist, dass ein Neuron in diesem Layer nur auf Reize in einer lokalen Umgebung des vorherigen Layers reagiert. Dies folgt dem biologischen Vorbild des rezeptiven Feldes. Zudem sind die Gewichte für alle Neuronen eines Convolutional Layers identisch (geteilte Gewichte, englisch: shared weights). Dies führt dazu, dass beispielsweise jedes Neuron im ersten Convolutional Layer codiert, zu welcher Intensität eine Kante in einem bestimmten lokalen Bereich der Eingabe vorliegt. Die Kantenerkennung als erster Schritt der Bilderkennung besitzt hohe biologische Plausibilität.[3] Aus den shared weights folgt unmittelbar, dass Translationsinvarianz eine inhärente Eigenschaft von CNNs ist.

Der mittels diskreter Faltung ermittelte Input eines jeden Neurons wird nun von einer Aktivierungsfunktion, bei CNNs üblicherweise Rectified Linear Unit, kurz ReLU ( $f(x)=\max(0,x)$ ), in den Output verwandelt, der die relative Feuerfrequenz eines echten Neurons modellieren soll. Da Backpropagation die Berechnung der Gradienten verlangt, wird in der Praxis eine differenzierbare Approximation von ReLU benutzt: $f(x)=\ln(1+e^{x})$

Analog zum visuellen Cortex steigt in tiefer gelegenen Convolutional Layers sowohl die Größe der rezeptiven Felder (siehe Sektion Pooling Layer) als auch die Komplexität der erkannten Features (beispielsweise Teile eines Gesichts).

Pooling Layer

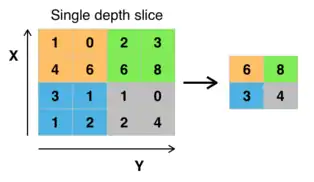
Max pooling mit einem 2×2-Filter und Schrittgröße = 2. Die Schrittgröße gibt an, wie viele Pixel der Filter pro Operation verschiebt.

Im folgenden Schritt, dem Pooling, werden überflüssige Informationen verworfen. Zur Objekterkennung in Bildern etwa ist die exakte Position einer Kante im Bild von vernachlässigbarem Interesse – die ungefähre Lokalisierung eines Features ist hinreichend. Es gibt verschiedene Arten des Poolings. Mit Abstand am stärksten verbreitet ist das Max-Pooling, wobei aus jedem 2 × 2 Quadrat aus Neuronen des Convolutional Layers nur die Aktivität des aktivsten (daher "Max") Neurons für die weiteren Berechnungsschritte beibehalten wird; die Aktivität der übrigen Neuronen wird verworfen (siehe Bild). Trotz der Datenreduktion (im Beispiel 75 %) verringert sich in der Regel die Performance des Netzwerks nicht durch das Pooling. Im Gegenteil, es bietet einige signifikante Vorteile:

Verringerter Platzbedarf und erhöhte Berechnungsgeschwindigkeit
Daraus resultierende Möglichkeit zur Erzeugung tieferer Netzwerke, die komplexere Aufgaben lösen können
Automatisches Wachstum der Größe der rezeptiven Felder in tieferen Convolutional Layers (ohne dass dafür explizit die Größe der Faltungsmatrizen erhöht werden müsste)
Präventionsmaßnahme gegen Overfitting

Alternativen wie das Mean-Pooling haben sich in der Praxis als weniger effizient erwiesen.[4]

Das biologische Pendant zum Pooling ist die laterale Hemmung im visuellen Cortex.

Fully-connected Layer

Nach einigen sich wiederholenden Einheiten bestehend aus Convolutional und Pooling Layer kann das Netzwerk mit einem (oder mehreren) Fully-connected Layer entsprechend der Architektur des mehrlagigen Perzeptrons abschließen. Dies wird vor allem bei der Klassifizierung angewendet. Die Anzahl der Neuronen im letzten Layer korrespondiert dann üblicherweise zu der Anzahl an (Objekt-)Klassen, die das Netz unterscheiden soll. Dieses, sehr redundante, sogenannte One-Hot-encoding hat den Vorteil, dass keine impliziten Annahmen über Ähnlichkeiten von Klassen gemacht werden.

Die Ausgabe der letzten Schicht des CNNs wird in der Regel durch eine Softmax-Funktion, einer translations- aber nicht skaleninvarianten Normalisierung über alle Neuronen im letzten Layer, in eine Wahrscheinlichkeitsverteilung überführt.

Training

CNNs werden in aller Regel überwacht trainiert. Während des Trainings wird dabei für jeden gezeigten Input der passende One-Hot-Vektor bereitgestellt. Via Backpropagation wird der Gradient eines jeden Neurons berechnet und die Gewichte werden in Richtung des steilsten Abfalls der Fehleroberfläche angepasst.

Interessanterweise haben drei vereinfachende Annahmen, die den Berechnungsaufwand des Netzes maßgeblich verringern und damit tiefere Netzwerke zulassen, wesentlich zum Erfolg von CNNs beigetragen.

Pooling – Hierbei wird der Großteil der Aktivität eines Layers schlicht verworfen.
ReLU – Die gängige Aktivierungsfunktion, die jeglichen negativen Input auf 0 projiziert.
Dropout – Eine Regularisierungsmethode beim Training, die Overfitting verhindert. Dabei werden pro Trainingsschritt zufällig ausgewählte Neuronen aus dem Netzwerk entfernt.

Expressivität und Notwendigkeit

Da CNNs eine Sonderform von mehrlagigen Perzeptrons darstellen,[5] sind sie prinzipiell identisch in ihrer Ausdrucksstärke.

Der Erfolg von CNNs lässt sich mit ihrer kompakten Repräsentation der zu lernenden Gewichte ("shared weights") erklären. Grundlage ist die Annahme, dass ein potentiell interessantes Feature (In Objekterkennung etwa Kanten) an jeder Stelle des Inputsignals (des Bildes) interessant ist. Während ein klassisches zweilagiges Perzeptron mit jeweils 1000 Neuronen pro Ebene für die Verarbeitung von einem Bild im Format 32 × 32 insgesamt 2 Millionen Gewichte benötigt, verlangt ein CNN mit zwei sich wiederholenden Einheiten, bestehend aus insgesamt 13.000 Neuronen, nur 160.000 (geteilte) zu lernende Gewichte, wovon der Großteil im hinteren Bereich (fully-connected Layer) liegt.

Neben dem wesentlich verringerten Arbeitsspeicherbedarf, haben sich geteilte Gewichte als robust gegenüber Translations-, Rotations-, Skalen- und Luminanzvarianz erwiesen.[5]

Um mithilfe eines mehrlagigen Perzeptrons eine ähnliche Performance in der Bilderkennung zu erreichen, müsste dieses Netzwerk jedes Feature für jeden Bereich des Inputsignals unabhängig erlernen. Dies funktioniert zwar ausreichend für stark verkleinerte Bilder (etwa 32 × 32), aufgrund des Fluchs der Dimensionalität scheitern MLPs jedoch an höher auflösenden Bildern.

Biologische Plausibilität

CNNs können als ein vom visuellen Cortex inspiriertes Konzept verstanden werden, sind jedoch weit davon entfernt, neuronale Verarbeitung plausibel zu modellieren.

Einerseits gilt das Herzstück von CNNs, der Lernmechanismus Backpropagation, als biologisch unplausibel, da es bis heute trotz intensiver Bemühungen nicht gelungen ist, neuronale Korrelate von backpropagation-ähnlichen Fehlersignalen zu finden.[6][7] Neben dem stärksten Gegenargument zur biologischen Plausibilität – der Frage, wie der Kortex Zugriff auf das Zielsignal (Label) bekommt – listen Bengio et al. weitere Gründe, darunter die binäre, zeitkontinuierliche Kommunikation biologischer Neurone sowie die Berechnung nicht-linearer Ableitungen der Vorwärtsneuronen[7].

Andererseits konnte durch Untersuchungen mit fMRT gezeigt werden, dass Aktivierungsmuster einzelner Schichten eines CNNs mit den Neuronenaktivitäten in bestimmten Arealen des visuellen Cortex korrelieren, wenn sowohl das CNN als auch die menschlichen Testprobanden mit ähnlichen Aufgaben aus der Bildverarbeitung konfrontiert werden.[8][9] Neuronen im primären visuellen Cortex, die sogenannten „simple cells“, reagieren auf Aktivität in einem kleinen Bereich der Retina. Dieses Verhalten wird in CNNs durch die diskrete Faltung in den convolutional Layers modelliert. Funktional sind diese biologischen Neuronen für die Erkennung von Kanten in bestimmten Orientierungen zuständig. Diese Eigenschaft der simple cells kann wiederum mithilfe von Gabor-Filtern präzise modelliert werden.[10][11] Trainiert man ein CNN zur Objekterkennung, konvergieren die Gewichte im ersten Convolutional Layer ohne jedes „Wissen“ über die Existenz von simple cells gegen Filtermatrizen, die Gabor-Filtern erstaunlich nahe kommen[12], was als Argument für die biologische Plausibilität von CNNs verstanden werden kann. Angesichts einer umfassenden statistischen Informationsanalyse von Bildern mit dem Ergebnis, dass Ecken und Kanten in verschiedenen Orientierungen die am stärksten voneinander unabhängigen Komponenten in Bildern – und somit die fundamentalsten Grundbausteine zur Bildanalyse – sind, ist dies jedoch zu erwarten.[13]

Somit treten die Analogien zwischen Neuronen in CNNs und biologischen Neuronen primär behavioristisch zutage, also im Vergleich zweier funktionsfähiger Systeme, wohingegen die Entwicklung eines "unwissenden" Neurons zu einem (beispielsweise) gesichtserkennenden Neuron in beiden Systemen diametralen Prinzipien folgt.

Anwendung

Seit dem Einsatz von Grafikprozessor-Programmierung können CNNs erstmals effizient trainiert werden.[14] Sie gelten als State-of-the-Art-Methode für zahlreiche Anwendungen im Bereich der Klassifizierung.

Bilderkennung

CNNs erreichen eine Fehlerquote von 0,23 % auf eine der am häufigsten genutzten Bilddatenbanken, MNIST, was (Stand 2016) der geringsten Fehlerquote aller jemals getesteten Algorithmen entspricht.[15]

Im Jahr 2012 verbesserte ein CNN (AlexNet) die Fehlerquote beim jährlichen Wettbewerb der Benchmark-Datenbank ImageNet (ILSVRC) von dem vormaligen Rekord von 25,8 % auf 16,4 %. Seitdem nutzen alle vorne platzierten Algorithmen CNN-Strukturen. Im Jahr 2016 wurde eine Fehlerquote < 3 % erreicht.[16]

Auch im Bereich der Gesichtserkennung konnten bahnbrechende Resultate erzielt werden.[17]

Spracherkennung

CNNs werden erfolgreich zur Spracherkennung eingesetzt und haben hervorragende Resultate in folgenden Bereichen erzielt:

semantisches Parsen[18]
Suchanfragenrückerkennung[19]
Satzmodellierung[20]
Satzklassifizierung[21]
Part-of-speech-Tagging[22]
Maschinelle Übersetzung (z. B. verwendet im Online-Dienst DeepL)[23]

Reinforcement Learning

Angewendet werden können CNNs auch im Bereich Reinforcement Learning, bei dem ein CNN mit Q-Learning kombiniert wird. Das Netzwerk wird darauf trainiert zu schätzen, welche Aktionen bei einem gegebenen Zustand zu welchem zukünftigen Gewinn führen. Durch die Verwendung eines CNNs können so auch komplexe, höher-dimensionale Zustandsräume betrachtet werden, wie etwa die Bildschirmausgabe eines Videospiels.[24]

Literatur

Ian Goodfellow, Yoshua Bengio, Aaron Courville: Deep Learning (= Adaptive Computation and Machine Learning). MIT Press, 2016, ISBN 978-0-262-03561-3, 9 Convolutional Networks (deeplearningbook.org).

Weblinks

TED-Talk: How we are teaching computers to understand pictures – Fei Fei Li, März 2015, abgerufen am 17. November 2016.
2D-Visualisierung der Aktivität eines zweilagigen CNNs, abgerufen am 17. November 2016.
Tutorial zur Implementierung eines CNN mithilfe der Python-Bibliothek TensorFlow
CNN-Tutorial der University of Stanford, inklusive Visualisierung erlernter Faltungsmatrizen, abgerufen am 17. November 2016.
Gradient-Based Learning Applied to Document Recognion, Y. Le Cun et al (PDF; 933 kB), erste erfolgreiche Anwendung eines CNN, abgerufen am 17. November 2016.
ImageNet Classification with Deep Convolutional Neural Networks, A. Krizhevsky, I. Sutskever and G. E. Hinton, AlexNet – Durchbruch in der Bilderkennung, Gewinner der ILSVRC-Challenge 2012.

Einzelnachweise

Masakazu Matsugu, Katsuhiko Mori, Yusuke Mitari, Yuji Kaneda: Subject independent facial expression recognition with robust face detection using a convolutional neural network. In: Neural Networks. 16, Nr. 5, 2003, S. 555–559. doi:10.1016/S0893-6080(03)00115-1. Abgerufen am 28. Mai 2017.
unknown: Convolutional Neural Networks (LeNet). Abgerufen am 17. November 2016 (englisch).
D. H. Hubel, T. N. Wiesel: Receptive fields and functional architecture of monkey striate cortex. In: The Journal of Physiology. 195, Nr. 1, 1. März 1968, ISSN 0022-3751, S. 215–243. doi:10.1113/jphysiol.1968.sp008455. PMID 4966457. PMC 1557912 (freier Volltext).
Dominik Scherer, Andreas C. Müller, Sven Behnke: Evaluation of Pooling Operations in Convolutional Architectures for Object Recognition. In: Artificial Neural Networks (ICANN), 20th International Conference on. Springer, 2010, S. 92–101.
Yann LeCun: LeNet-5, convolutional neural networks. Abgerufen am 17. November 2016.
A more biological plausible learning rule than Backpropagation applied to a network model of cortical area 7d
Yoshua Bengio: Towards Biologically Plausible Deep Learning. Abgerufen am 29. Dezember 2017 (englisch).
Haiguang Wen: Neural Encoding and Decoding with Deep Learning for Dynamic Natural Vision. Abgerufen am 17. September 2017 (englisch).
Sandy Wiraatmadja: Modeling the Visual Word Form Area Using a Deep Convolutional Neural Network. Abgerufen am 17. September 2017 (englisch).
J. G. Daugman: Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters. In: Journal of the Optical Society of America A, 2 (7): 1160–1169, July 1985.
S. Marčelja: Mathematical description of the responses of simple cortical cells. In: Journal of the Optical Society of America. 70, Nr. 11, 1980, S. 1297–1300. doi:10.1364/JOSA.70.001297.
ImageNet Classification with Deep Convolutional Neural Networks, A. Krizhevsky, I. Sutskever and G. E. Hinton (PDF; 1,4 MB)
The “Independent Components” of Scenes are Edge Filters (PDF; 1,3 MB), A. Bell, T. Sejnowski, 1997, abgerufen am 17. November 2016.
ImageNet Classification with Deep Convolutional Neural Networks (PDF; 1,4 MB)
Dan Ciresan, Ueli Meier, Jürgen Schmidhuber: Multi-column deep neural networks for image classification. In: Institute of Electrical and Electronics Engineers (IEEE) (Hrsg.): 2012 IEEE Conference on Computer Vision and Pattern Recognition. , New York, NY, Juni 2012, S. 3642–3649. arxiv:1202.2745v1. doi:10.1109/CVPR.2012.6248110. Abgerufen am 9. Dezember 2013.
ILSVRC 2016 Results
Improving multiview face detection with multi-task deep convolutional neural networks
A Deep Architecture for Semantic Parsing. Abgerufen am 17. November 2016 (englisch).
Learning Semantic Representations Using Convolutional Neural Networks for Web Search – Microsoft Research. In: research.microsoft.com. Abgerufen am 17. November 2016.
A Convolutional Neural Network for Modelling Sentences. 17. November 2016.
Convolutional Neural Networks for Sentence Classification. Abgerufen am 17. November 2016.
Natural Language Processing (almost) from Scratch. Abgerufen am 17. November 2016.
heise online: Maschinelle Übersetzer: DeepL macht Google Translate Konkurrenz. 29. August 2017, abgerufen am 18. September 2017.
Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A. Rusu, Joel Veness: Human-level control through deep reinforcement learning. In: Nature. Band 518, Nr. 7540, Februar 2015, ISSN 0028-0836, S. 529–533, doi:10.1038/nature14236 (nature.com [abgerufen am 13. Juni 2018]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[robust_face_detection-1] Masakazu Matsugu, Katsuhiko Mori, Yusuke Mitari, Yuji Kaneda: Subject independent facial expression recognition with robust face detection using a convolutional neural network. In: Neural Networks. 16, Nr. 5, 2003, S. 555–559. doi:10.1016/S0893-6080(03)00115-1. Abgerufen am 28. Mai 2017.

[deeplearning-2] unknown: Convolutional Neural Networks (LeNet). Abgerufen am 17. November 2016 (englisch).

[3] D. H. Hubel, T. N. Wiesel: Receptive fields and functional architecture of monkey striate cortex. In: The Journal of Physiology. 195, Nr. 1, 1. März 1968, ISSN 0022-3751, S. 215–243. doi:10.1113/jphysiol.1968.sp008455. PMID 4966457. PMC 1557912 (freier Volltext).

[Scherer-4] Dominik Scherer, Andreas C. Müller, Sven Behnke: Evaluation of Pooling Operations in Convolutional Architectures for Object Recognition. In: Artificial Neural Networks (ICANN), 20th International Conference on. Springer, 2010, S. 92–101.

[LeCun-5] Yann LeCun: LeNet-5, convolutional neural networks. Abgerufen am 17. November 2016.

[6] A more biological plausible learning rule than Backpropagation applied to a network model of cortical area 7d

[Biologically_plausible_DL-7] Yoshua Bengio: Towards Biologically Plausible Deep Learning. Abgerufen am 29. Dezember 2017 (englisch).

[Neural_encoding_with_DL-8] Haiguang Wen: Neural Encoding and Decoding with Deep Learning for Dynamic Natural Vision. Abgerufen am 17. September 2017 (englisch).

[Modeling_VFWA_with_a_CNN-9] Sandy Wiraatmadja: Modeling the Visual Word Form Area Using a Deep Convolutional Neural Network. Abgerufen am 17. September 2017 (englisch).

[10] J. G. Daugman: Uncertainty relation for resolution in space, spatial frequency, and orientation optimized by two-dimensional visual cortical filters. In: Journal of the Optical Society of America A, 2 (7): 1160–1169, July 1985.

[11] S. Marčelja: Mathematical description of the responses of simple cortical cells. In: Journal of the Optical Society of America. 70, Nr. 11, 1980, S. 1297–1300. doi:10.1364/JOSA.70.001297.

[12] ImageNet Classification with Deep Convolutional Neural Networks, A. Krizhevsky, I. Sutskever and G. E. Hinton (PDF; 1,4 MB)

[13] The “Independent Components” of Scenes are Edge Filters (PDF; 1,3 MB), A. Bell, T. Sejnowski, 1997, abgerufen am 17. November 2016.

[14] ImageNet Classification with Deep Convolutional Neural Networks (PDF; 1,4 MB)

[mcdns-15] Dan Ciresan, Ueli Meier, Jürgen Schmidhuber: Multi-column deep neural networks for image classification. In: Institute of Electrical and Electronics Engineers (IEEE) (Hrsg.): 2012 IEEE Conference on Computer Vision and Pattern Recognition. , New York, NY, Juni 2012, S. 3642–3649. arxiv:1202.2745v1. doi:10.1109/CVPR.2012.6248110. Abgerufen am 9. Dezember 2013.

[16] ILSVRC 2016 Results

[17] Improving multiview face detection with multi-task deep convolutional neural networks

[18] A Deep Architecture for Semantic Parsing. Abgerufen am 17. November 2016 (englisch).

[19] Learning Semantic Representations Using Convolutional Neural Networks for Web Search – Microsoft Research. In: research.microsoft.com. Abgerufen am 17. November 2016.

[20] A Convolutional Neural Network for Modelling Sentences. 17. November 2016.

[21] Convolutional Neural Networks for Sentence Classification. Abgerufen am 17. November 2016.

[22] Natural Language Processing (almost) from Scratch. Abgerufen am 17. November 2016.

[23] se online: Maschinelle Übersetzer: DeepL macht Google Translate Konkurrenz. 29. August 2017, abgerufen am 18. September 2017.

[24] Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A. Rusu, Joel Veness: Human-level control through deep reinforcement learning. In: Nature. Band 518, Nr. 7540, Februar 2015, ISSN 0028-0836, S. 529–533, doi:10.1038/nature14236 (nature.com [abgerufen am 13. Juni 2018]).