Überwachtes Lernen

Überwachtes Lernen ist ein Teilgebiet des maschinellen Lernens. Mit Lernen ist dabei die Fähigkeit einer künstlichen Intelligenz gemeint, Gesetzmäßigkeiten nachzubilden. Die Ergebnisse sind durch Naturgesetze oder Expertenwissen bekannt und werden benutzt, um das System anzulernen.

Ein Lernalgorithmus versucht, eine Hypothese zu finden, die möglichst zielsichere Voraussagen trifft. Unter Hypothese ist dabei eine Abbildung zu verstehen, die jedem Eingabewert den vermuteten Ausgabewert zuordnet.[1]

Die Methode richtet sich also nach einer im Vorhinein festgelegten zu lernenden Ausgabe, deren Ergebnisse bekannt sind. Die Ergebnisse des Lernprozesses können mit den bekannten, richtigen Ergebnissen verglichen, also „überwacht“, werden.[2]

Liegen die Ergebnisse der Ausgabe in einer stetigen Verteilung vor, deren Ergebnisse beliebige quantitative Werte eines vorgegebenen Wertebereiches annehmen kann, spricht man meistens von einem Regressionsproblem.[3]

Ein Beispiel für ein solches Regressionsproblem ist die Vorhersage der Preisentwicklung von Häusern auf Basis von bestimmten Variablen oder das Bestimmen des Alters einer Person aus anderen Informationen über die Person. Es geht demnach meistens um Vorhersagen.[3]

Liegen die Ergebnisse hingegen in diskreter Form vor bzw. sind die Werte qualitativ, spricht man von einem Klassifikationsproblem. Ein Beispiel hierfür ist, zu bestimmen, ob es sich bei einer E-Mail um Spam oder keinen Spam handelt.[4]

Dieser folgende Artikel beschreibt das Vorgehen bei der Implementierung von überwachtem Lernen und stellt einige Methoden zur Lösung von Regressionsproblemen respektive zur Lösung von Klassifikationsproblemen vor.

Definitionen

Um im folgenden mathematische Zusammenhänge besser darstellen zu können, werden folgende Definitionen verwendet[5]:

x^{(i)}

= Input-Variablen (auch „erklärende Variablen“ genannt)

y^{(i)}

= Output/Ziel-Variablen (auch „erklärte Variablen“ genannt)

(x^{(i)},y^{(i)})

= Trainingspaar/Trainingsbeispiel

{(x^{(i)},y^{(i)});i=1,\ldots ,m}

= Datensatz der zum Lernen verwendet wird (auch Lerndatensatz genannt)

h(x)

= Die Hypothesenfunktion, die vom Algorithmus gelernt werden soll, um

y

möglichst genau zu approximieren

Vorgehen

Um ein bestimmtes Problem mit überwachtem Lernen zu lösen, muss man die folgenden Schritte durchführen:

Die Art der Trainingsbeispiele bestimmen. Das heißt, es muss zunächst bestimmt werden, welche Art von Daten der Trainingsdatensatz enthalten soll. Bei der Handschriftanalyse kann es sich z. B. um ein einzelnes handschriftliches Zeichen, ein ganzes handschriftliches Wort oder eine ganze Zeile Handschrift handeln.
Eine Datenerhebung der vorangegangenen Auswahl entsprechend durchführen. Es müssen sowohl die erklärenden Variablen als auch die erklärten Variablen erhoben werden. Diese Erhebung kann von menschlichen Experten, durch Messungen und andere Methoden vollzogen werden.
Die Genauigkeit der gelernten Funktion hängt stark davon ab, wie die erklärenden Variablen dargestellt werden. Typischerweise werden diese in einen Vektor transformiert, der eine Reihe von Merkmalen enthält, die das Objekt beschreiben. Die Anzahl der Features sollte nicht zu groß sein; sie sollte aber genügend Informationen enthalten, um die Ausgabe genau vorhersagen zu können.
Daraufhin muss die Struktur der gelernten Funktion und der dazugehörige Lernalgorithmus bestimmt werden. Bei einem Regressionsproblem zum Beispiel sollte an dieser Stelle entschieden werden, ob eine Funktion mit oder ohne Parameter besser geeignet ist, um die Approximation durchzuführen.
Anschließend wird der Lernalgorithmus auf dem gesammelten Trainingsdatensatz ausgeführt. Einige überwachte Lernalgorithmen erfordern vom Anwender die Festlegung bestimmter Regelparameter. Diese Parameter können entweder durch die Optimierung einer Teilmenge des Datensatzes (Validierungsdatensatz genannt) oder durch Kreuzvalidierung angepasst werden.
Als letztes muss die Genauigkeit der gelernten Funktion bestimmt werden. Nach der Parametrierung und dem Erlernen der Parameter sollte die Leistung der resultierenden Funktion an einem Test-Datensatz gemessen werden, der vom Trainingsdatensatz getrennt ist.

Es steht eine breite Palette von überwachten Lernalgorithmen zur Verfügung, von denen jeder seine Stärken und Schwächen hat. Es gibt dabei keinen Lernalgorithmus, der bei allen überwachten Lernproblemen am besten funktioniert (siehe No-free-Lunch-Theoreme). Im Folgenden werden sowohl für Regressions- als auch für Klassifikationsprobleme die geläufigsten Lernalgorithmen vorgestellt und weitere Algorithmen verlinkt.

Regressionsprobleme

Das Ziel von überwachtem Lernen im Falle von Regressionsproblemen ist meist, auf Basis von bestimmten erklärenden Variablen wie Größe oder Farbe eines Hauses etwas über diesen Sachverhalt vorauszusagen. Der Sachverhalt kann dabei grundlegend verschieden sein, beispielsweise der Preis von Häusern in bestimmter Umgebung oder die Entwicklung des Preises einer Aktie am nächsten Tag. Das Ziel ist es dementsprechend den Zusammenhang zwischen der erklärenden und der erklärten Variable anhand eines Trainingsdatensatzes zu erlernen und mit Hilfe dieses Zusammenhangs zukünftige Ereignisse, die noch nicht bekannt sind, vorherzusagen. Ein Beispiel für einen solchen Lernalgorithmus der Vorhersagen treffen kann, ist die lineare Regression.

Lineare Regression

Die lineare Regression ist die geläufigste Form zur Durchführung einer Regression.[3] Das dazu verwendete Modell ist linear in den Parametern, wobei die abhängige Variable eine Funktion der unabhängigen Variablen ist.[6] Bei der Regression sind die Ausgaben der unbekannten Funktion verrauscht

y=h_{\theta }(x)+\varepsilon

,

wobei $f(x)\in \mathbb {R}$ die unbekannte Funktion darstellt und $\varepsilon$ für zufälliges Rauschen steht. Die Erklärung für das Rauschen liegt darin, dass es zusätzliche verborgene Variablen gibt, die unbeobachtbar sind.[7] Hierzu wird die folgende Regressionsfunktion verwendet:

h_{\theta }(x)=\theta _{0}+\theta _{1}x_{1}+\ldots +\theta _{n}x_{n}

bzw. in Vektorschreibweise:

h_{\theta }(x)=\sum _{i=0}^{n}\theta _{i}x_{i}={\boldsymbol {\theta }}^{\top }\mathbf {x}

Die $\theta _{i}$ sind dabei die Parameter der Funktion und $x$ ist der Vektor, welcher die erklärenden Variablen enthält. Dementsprechend gewichten die Parameter die einzelnen erklärenden Variablen und werden deshalb auch oft als Regressionsgewichte bezeichnet.

Um nun aus den erklärenden Variablen eine möglichst genaue Annäherung an den Output $y$ zu erhalten, muss eine sogenannte „Kostenfunktion“ aufgestellt werden.

Diese Funktion beschreibt die mittlere quadratische Abweichung, die dadurch entsteht, dass die Hypothesenfunktion die zu erklärende Variable $y$ nur approximiert und nicht genau darstellt. Insofern muss die Kostenfunktion, welche durch die folgende Gleichung beschrieben wird:

J(\theta )={\frac {1}{m}}\sum _{i=1}^{m}(h_{\theta }(x^{(i)})-y^{(i)})^{2}

angewendet werden, um den Fehler, der bei jeder Approximation von $y$ gemacht wird, zu berechnen.

Das Ziel ist es nun die Kostenfunktion zu minimieren.

Um die Funktion zu minimieren, müssen die Parameter so gewählt werden, dass sie die jeweiligen x-Werte richtig gewichten, um dem gewünschten y-Wert möglichst nahe zu kommen.

Das Minimum kann an dieser Stelle auf zwei verschiedene Weisen berechnet werden.

Eine Methode ist das sogenannte Gradientenverfahren.

Diese Methode umfasst folgende Schritte[8]:

Es werden beliebige Werte für die Parameter gewählt.
An diesem Punkt wird die Ableitung der Kostenfunktion gebildet und die steilste Steigung ermittelt
Man geht diese Steigung in die negative Richtung entlang. Dabei wird die Größe der Schritte durch eine Lernrate bestimmt.
Dieser Prozess wird so lange wiederholt bis man am Minimum der Kostenfunktion angekommen ist.

Dies ist in der folgenden Gleichung für ein einzelnes Beispiel dargestellt (Alpha steht hierbei für die Lernrate):

\theta _{j}:=\theta _{j}+\alpha (y^{(i)}-h_{\theta }(x^{(i)}))x_{j}^{(i)}

Diese Gleichung wird so oft wiederholt bis $y(i)-h(x)=0$ bzw. bis diese Differenz minimiert wurde und der Parameter somit seinen optimalen Wert gefunden hat.

Eine weitere Methode, die verwendet werden kann, sind die sogenannten Normalgleichungen (siehe Multiple lineare Regression). Mit dieser kann die Minimierung der Kostenfunktion explizit und ohne Rückgriff auf einen iterativen Algorithmus durchgeführt werden, indem die folgende Formel implementiert wird:

\mathbf {\theta } =(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {y}

Diese Formel liefert uns die optimalen Werte der Parameter.

In der folgenden Tabelle[8] sind die Vor- und Nachteile von Gradientenverfahren und der Normalgleichung dargestellt.

Gradientenverfahren	Normalverteilung
Die Lernrate Alpha muss festgelegt werden	Es wird kein Alpha benötigt
Benötigt viele Schritte und Wiederholungen	Kommt ohne Wiederholungen aus
Funktioniert gut auch bei vielen Daten	Ab 10000 Beobachtungen wird die Berechnung langsam und die erforderte Rechenleistung sehr groß, da die Inverse gebildet werden muss.

Weitere Beispiele für überwachte Lernalgorithmen zur Lösung von Regressionsproblemen

Klassifikationsprobleme

Im Gegensatz zu Regressionsproblemen erkennt man Klassifikationsprobleme daran, dass der Output y nur wenige diskrete Werte annehmen kann. Meistens liegen diese Werte in qualitativer Form vor, beispielsweise, wenn es darum geht auf der Basis von mehreren erklärenden Variablen zu bestimmen, ob es sich bei einer E-Mail um Spam oder keinen Spam handelt. In diesem Beispiel wären die erklärenden Variablen dann $x^{(i)}$ und der Output $y$ wäre 1, wenn es sich um eine Spam-E-Mail handelt und 0, wenn keine Spam-E-Mail vorliegt.

Man unterscheidet zudem zwischen Binären Klassifikationsproblemen und Klassifikationsproblemen bei denen multiple Klassen vorliegen. Ein Beispiel hierfür wäre zu klassifizieren von welcher von drei Marken ein gekauftes Produkt ist (Die Klassen sind in diesem Fall Marke A, B oder C).

Logistische Regression

Die geläufigste Methode, um Klassifikationsprobleme im überwachten maschinellen Lernen zu bewältigen ist die logistische Regression. Obwohl es sich hier, wie der Name sagt, ebenfalls um eine Regression handelt, ist sie sehr gut dafür geeignet, einem Computer-Programm die Lösung von Klassifikationsproblemen beizubringen.[8]

Wie bereits an dem Beispiel zur Klassifikation von Spam-E-Mails erklärt, nimmt der Output entweder Werte von 1 oder 0 an. Würde man nun zur Lösung dieses Klassifikationsproblems eine lineare Regression verwenden, dann würde man vermutlich viele Werte erhalten die über 1 oder unter 0 liegen.

Die logistische Regression hingegen verwendet die Sigmoidfunktion, gegeben durch folgende Gleichung:

g(z)={\frac {\exp(z)}{1+\exp(z)}}={\frac {1}{1+\exp(-z)}}

.

Dies lässt sich auf die Hypothesenfunktion folgendermaßen anwenden:

h_{\theta }(x)=g(\theta ^{\top }x)={\frac {1}{1+\exp(-{\boldsymbol {\theta }}^{\top }\mathbf {x} )}}

Da g(z) immer Werte zwischen 0 und 1 liefert, liegen auf diese Weise auch die Werte von $h(x)$ zwischen 0 und 1. Dies lässt sich im folgenden Graphen erkennen:

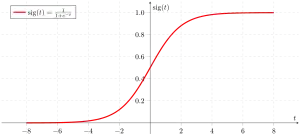
Die Werte der Sigmoid Funktion liegen immer zwischen 0 und 1 und werden im Kontext der logistischen Regression als Wahrscheinlichkeit für die Zugehörigkeit zu einer bestimmten Klasse interpretiert

Die Einteilung einer Beobachtung in eine bestimmte Klasse erfolgt folgendermaßen:

g(z)\geq 0{,}5\Rightarrow Y=1

g(z)<0{,}5\Rightarrow Y=0

Um nun eine möglichst akkurate Zuordnung der Inputs in die Zielklassen zu ermöglichen, müssen die Parameter wie bei der linearen Regression optimiert werden.

Wir nehmen dazu den folgenden Zusammenhang an:

P(y=1\mid x;\theta )=h_{\theta }(x)

$P(y=0\mid x;\theta )=1-h_{\theta }(x)$

Diese Gleichungen bedeuten, dass die Wahrscheinlichkeit, dass ein bestimmter Input der Klasse 1 angehört, durch das Ergebnis die Hypothesenfunktion $h(x)$ gegeben ist.

Daraus folgt, dass die allgemeine bedingte Wahrscheinlichkeit für einen bestimmten Output y unter der Bedingung eines bestimmten Inputs x durch die folgende Funktion gegeben ist:

p(y\mid x;\theta )=(h_{\theta }(x))^{y}(1-h_{\theta }(x))^{1-y}

Multipliziert man diese Wahrscheinlichkeit nun für alle Beobachtungen in dem Datensatz zusammen, erhält man die Formel für die sogenannte „Likelihood“ eines bestimmten Parameters.

L(\theta )=p(\mathbf {y} \mid X;\theta )

=\prod _{i=1}^{m}p(y^{(i)}\mid x^{(i)};\theta )

=\prod _{i=1}^{m}(h_{\theta }(x^{(i)}))^{y^{(i)}}(1-h_{\theta }(x^{(i)}))^{1-y^{(i)}}

Hat man bei der linearen Regression die mittlere quadratische Abweichung minimiert, um die optimalen Werte für die Parameter zu erhalten, maximiert man bei der logistischen Regression die Likelihood-Funktion, um die optimalen Werte der Parameter zu erhalten. Dieses Verfahren wird als Maximum-Likelihood-Methode bezeichnet.

Um die Maximierung zu erleichtern, wird oft auch die Log-Likelihood-Funktion gebildet:

\ell (\theta )=\log L(\theta )

=\sum _{i=1}^{m}y^{(i)}\log h(x^{(i)})+(1-y^{(i)})\log(1-h(x^{(i)}))

Von dieser Funktion muss nun die Steigung berechnet werden, wozu der sogenannte gradient ascent verwendet wird. Er funktioniert ähnlich wie das bei der linearen Regression angewendete Gradientenverfahren, außer dass er eine Addition anstatt einer Subtraktion durchführt, da die Log-Likelihood-Funktion maximiert und nicht minimiert werden soll. Durch die folgende Gleichung erhält man somit den optimierten Wert des Parameters:

\theta _{j}:=\theta _{j}+\alpha (y^{(i)}-h_{\theta }(x^{(i)}))x_{j}^{(i)}

Perzeptron-Algorithmus

In den 1960er Jahren wurde der sogenannte Perzeptron-Algorithmus entwickelt. Er wurde entsprechend den Vorstellungen der damaligen Zeit über die Funktionsweise des Gehirns aufgebaut.[5]

Der wesentliche Unterschied zwischen dem Perzepton Algorithmus und der logistischen Regression ist, dass die Funktion $h(x)$ entweder den Wert 0 oder den Wert 1 annimmt, aber nicht wie bei der logistischen Regression einen beliebigen Wert zwischen 0 und 1.[5] Dies wird sichergestellt, indem die Funktion $g(z)$ nicht wie bei der logistischen Regression mit Hilfe einer Sigmoid Funktion einen Wert zwischen 0 und 1 annimmt, sondern entsprechend der Formeln:

g(z)=1

wenn

z\geq 0

g(z)=0

wenn

z<0

entweder genau 0 oder genau 1 entspricht.

Es gilt weiterhin:

h_{\theta }(x)=g({\boldsymbol {\theta }}^{\top }\mathbf {x} )

Und die Updating Regel ist ebenfalls beschrieben durch:

\theta _{j}:=\theta _{j}+\alpha (y^{(i)}-h_{\theta }(x^{(i)}))x_{j}^{(i)}

Diese Gleichung sieht sehr ähnlich aus zu den Lernprozessen der vorherigen Algorithmen. Es muss jedoch beachtet werden, dass durch die Definition von $g(z)$ Perzeptron einen nicht sonderlich fließenden Lernprozess hat, da der Fehler, der entsteht, wenn ein Input durch den Algorithmus falsch klassifiziert wird, entweder wesentlich überschätzt oder unterschätzt werden kann, in dem $h(x)$ nur 1 oder 0 annehmen kann. So wird beispielsweise, wenn $z=-0{,}0001$ beträgt sowie wenn $z=-100$ beträgt in beiden Fällen die Klasse 0 vorhergesagt. Gehören die Beobachtungen allerdings in Wahrheit Klasse 1 an, so werden die Parameter in beiden Fällen, um den gleichen Wert angepasst.[5]

Weitere Beispiele für überwachte Lernalgorithmen zur Klassifikation

Bayes-Klassifikator
Naiver Bayes-Klassifikator
Nächste-Nachbarn-Klassifikation
Diskriminanzanalyse
Künstliches neuronales Netz
Gradient Boosted Trees (Entscheidungsbaum)

Zu berücksichtigende Faktoren

Verzerrung-Varianz-Dilemma

Bei überwachtem Lernen kommt es oftmals zu einem Kompromiss zwischen Verzerrung und Varianz.[9] Die Varianz bezieht sich auf den Betrag, um den sich $h(x)$ verändern würde, wenn wir es mit Hilfe eines anderen Trainingsdatensatzes schätzen würden. Da die Trainingsdaten zur Anpassung an die statistische Lernmethode verwendet werden, führen unterschiedliche Trainingsdatensätze zu unterschiedlichen $h(x)$ . Im Idealfall sollte die Schätzung für $y$ jedoch nicht zu viel zwischen den Trainingssets variieren. Hat eine Methode jedoch eine hohe Varianz, dann können kleine Änderungen in den Trainingsdaten zu einer viel schlechteren Abbildung des Testdatensatzes führen. Grundsätzlich haben flexiblere statistische Methoden eine höhere Varianz, da sie den Trainingsdatensatz sehr gut abbilden, dadurch aber viele Fehler machen, wenn sie zuvor unbekannte Daten vorhersagen müssen.[3]

Auf der anderen Seite bezieht sich die Verzerrung auf den Fehler, der durch die Annäherung an ein reales Problem, das sehr kompliziert sein kann, durch ein einfacheres Modell entstehen kann. Zum Beispiel geht die lineare Regression davon aus, dass ein Problem vorliegt, das eine lineare Beziehung zwischen $Y$ und $X_{1},X_{2},\ldots ,X_{p}$ aufweist. In der Realität liegen jedoch selten Probleme vor die eine einfache lineare Beziehung aufweisen, und so führt die Durchführung einer linearen Regression zweifellos zu einer gewissen Verzerrung zwischen $h(x)$ und $y$ .[3]

Menge an Daten und Komplexität der „wahren Funktion“

Die zweite Frage ist die Menge der verfügbaren Trainingsdaten in Relation zur Komplexität der „wahren Funktion“ (Klassifikator- oder Regressionsfunktion). Wenn die wahre Funktion einfach ist, dann kann ein „unflexibler“ Lernalgorithmus mit hoher Verzerrung und geringer Varianz aus einer kleinen Datenmenge lernen. Wenn die wahre Funktion jedoch sehr komplex ist (z. B. weil sie komplexe Interaktionen zwischen vielen verschiedenen Eingabemerkmalen beinhaltet und sich in verschiedenen Teilen des Eingaberaums unterschiedlich verhält), dann wird die Funktion nur aus einer sehr großen Menge von Trainingsdaten und unter Verwendung eines „flexiblen“ Lernalgorithmus mit geringer Vorspannung und hoher Varianz erlernbar sein.[3]

Ausnahmeerscheinungen in den Ausgabewerten

Ein weiteres mögliches Problem sind sogenannte „Ausreißer“ in den Zielwerten. Wenn die Zielwerte $y$ oft falsch sind (aufgrund von menschlichen Fehlern oder Sensorfehlern), dann sollte der Lernalgorithmus nicht versuchen, eine Funktion zu finden, die genau zu den Trainingsbeispielen passt. Der Versuch, die Daten zu sorgfältig anzupassen, führt zu einer Überanpassung. Auch wenn keine Messfehler vorliegen, kann es zu Fehlern kommen, wenn die zu erlernende Funktion für den gewählten Lernalgorithmus zu komplex ist. In einer solchen Situation, kann ein Teil der Zielfunktion nicht modelliert werden, wodurch die Trainingsdaten nicht korrekt abgebildet werden können. Wenn eine der beiden Probleme vorliegt, ist es besser, mit einer stärkeren Verzerrung und einer niedrigeren Varianz zu arbeiten.

In der Praxis gibt es mehrere Ansätze Probleme mit den Ausgabewerten zu verhindern, wie z. B. frühzeitiges Anhalten des Algorithmus zur Vermeidung von Überanpassung sowie das Erkennen und Entfernen der Ausreißer vor dem Training des überwachten Lernalgorithmus. Es gibt mehrere Algorithmen, die Ausreißer identifizieren und deren Entfernen ermöglichen.[3]

Siehe auch

Einzelnachweise

Rostamizadeh, Afshin., Talwalkar, Ameet.: Foundations of machine learning. MIT Press, Cambridge, MA 2012, ISBN 978-0-262-01825-8.
Guido, Sarah, Rother, Kristian: Einführung in Machine Learning mit Python Praxiswissen Data Science. Heidelberg, ISBN 978-3-96009-049-6.
James, Gareth (Gareth Michael): An introduction to statistical learning : with applications in R. New York, NY, ISBN 978-1-4614-7137-0.
Alex Smola: Introduction to Machine Learning. Hrsg.: Cambridge University Press. Cambridge 2008, ISBN 0-521-82583-0.
Andrew Ng: CS229 Lecture notes. (PDF) (Nicht mehr online verfügbar.) 2012, ehemals im Original; abgerufen am 12. November 2017.@1@2Vorlage:Toter Link/cs229.stanford.edu (Seite nicht mehr abrufbar, Suche in Webarchiven)
James, Gareth (Gareth Michael): An introduction to statistical learning : with applications in R. New York, NY, ISBN 978-1-4614-7137-0.
Ethem Alpaydin: Maschinelles Lernen., 2., erweiterte Auflage, De Gruyter, Berlin 2019, ISBN 978-3-11-061789-4 (abgerufen über De Gruyter Online). S. 37
Andrew Ng: Introduction to Machine Learning. Abgerufen am 12. November 2017.
S. Geman, E. Bienenstock, and R. Doursat: Neural networks and the bias/variance dilemma. In: Neural Computation. Band 4, S. 1–58.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Rostamizadeh, Afshin., Talwalkar, Ameet.: Foundations of machine learning. MIT Press, Cambridge, MA 2012, ISBN 978-0-262-01825-8.

[2] Guido, Sarah, Rother, Kristian: Einführung in Machine Learning mit Python Praxiswissen Data Science. Heidelberg, ISBN 978-3-96009-049-6.

[:0-3] James, Gareth (Gareth Michael): An introduction to statistical learning : with applications in R. New York, NY, ISBN 978-1-4614-7137-0.

[4] Alex Smola: Introduction to Machine Learning. Hrsg.: Cambridge University Press. Cambridge 2008, ISBN 0-521-82583-0.

[:1-5] Andrew Ng: CS229 Lecture notes. (PDF) (Nicht mehr online verfügbar.) 2012, ehemals im Original; abgerufen am 12. November 2017.@1@2Vorlage:Toter Link/cs229.stanford.edu (Seite nicht mehr abrufbar, Suche in Webarchiven)

[6] James, Gareth (Gareth Michael): An introduction to statistical learning : with applications in R. New York, NY, ISBN 978-1-4614-7137-0.

[7] Ethem Alpaydin: Maschinelles Lernen., 2., erweiterte Auflage, De Gruyter, Berlin 2019, ISBN 978-3-11-061789-4 (abgerufen über De Gruyter Online). S. 37

[:2-8] Andrew Ng: Introduction to Machine Learning. Abgerufen am 12. November 2017.

[9] S. Geman, E. Bienenstock, and R. Doursat: Neural networks and the bias/variance dilemma. In: Neural Computation. Band 4, S. 1–58.