Evolutionärer Algorithmus

Evolutionäre Algorithmen (EA) sind eine Klasse von stochastischen, metaheuristischen Optimierungsverfahren, deren Funktionsweise von der Evolution natürlicher Lebewesen inspiriert ist.

Die Antenne der Space Technology 5 Satelliten wurde mit einem EA entwickelt.[1]

In Anlehnung an die Natur werden Lösungskandidaten für ein bestimmtes Problem künstlich evolviert, EA sind also naturanaloge Optimierungsverfahren. Die Zuordnung zu den stochastischen und metaheuristischen Algorithmen bedeutet vor allem, dass EA meist nicht die beste Lösung für ein Problem finden, aber bei Erfolg eine hinreichend gute, was in der Praxis vor allem bei NP-vollständigen Problemen bereits wünschenswert ist. Die Verfahren verschiedener EA unterscheiden sich untereinander in erster Linie durch die genutzten Selektions-, Rekombinations- und Mutationsoperatoren, das Genotyp-Phänotyp-Mapping sowie die Problemrepräsentation.

Die ersten praktischen Implementierungen evolutionärer Algorithmen wurden Ende der 1950er Jahre veröffentlicht,[2] allerdings äußerten sich bereits in den vorhergehenden Jahrzehnten Wissenschaftler zum Potenzial der Evolution für maschinelles Lernen.[3]

Es gibt vier Hauptströmungen, deren Konzepte zumindest historisch voneinander zu unterscheiden sind:

genetische Algorithmen
Evolutionsstrategien
genetische Programmierung und
evolutionäre Programmierung

Heute verschwimmen diese Abgrenzungen zunehmend. Für eine bestimmte Anwendung wird ein EA geeignet entworfen, wobei in den letzten Jahrzehnten viele verschiedene Algorithmen und einzelne Operatoren entwickelt wurden, die heute benutzt werden können.

Die Anwendungen von EA gehen über Optimierung und Suche hinaus und finden sich auch in Kunst, Modellierung und Simulation, insbesondere auch bei der Untersuchung evolutionsbiologischer Fragestellungen.

Einführung

Evolutionäre Algorithmen werden vorrangig zur Optimierung oder Suche eingesetzt. Konkrete Probleme, die mit EA gelöst werden, sind äußerst divers: z. B. Die Entwicklung von Sensornetzen, Aktienmarktanalyse, RNA-Strukturvorhersage,[4] Schedulingprobleme[5], Designoptimierung[6] (siehe auch obiges Bild der Satellitenantenne) oder Roboterbahnplanung.[7] Auch bei Problemen, über deren Beschaffenheit nur wenig Wissen vorliegt, können sie zufriedenstellende Lösungen finden. Dies ist auf die Eigenschaften ihres natürlichen Vorbildes zurückzuführen.

Natürliches Vorbild	Evolutionärer Algorithmus	Beispiel
Organismus	Lösungskandidat	Autotür
Fortpflanzungserfolg	Wert der Fitnessfunktion	Strömungswiderstand
Natürliche Mutation	Mutation	Änderung der Form

In der biologischen Evolution sind die Gene von Organismen natürlich vorkommenden Mutationen ausgesetzt, wodurch genetische Variabilität entsteht. Mutationen können sich positiv, negativ oder gar nicht auf Erben auswirken. Da es zwischen erfolgreichen Individuen zur Fortpflanzung (Rekombination) kommt, können sich Arten über lange Zeiträume an einen vorliegenden Selektionsdruck anpassen (z. B. Klimaveränderungen oder die Erschließung einer ökologischen Nische). Diese vereinfachte Vorstellung wird in der Informatik idealisiert und künstlich im Computer nachgebildet. Dabei wird die Güte eines Lösungskandidaten explizit mit einer Fitnessfunktion berechnet, sodass verschiedene Kandidaten vergleichbar sind.

Entsprechend dem natürlichen Vorbild gibt es bei den EAs Individuen, die aus einem Genom bestehen, welches die zu bestimmenden Eigenschaften der gesuchten Lösung in geeigneter Weise enthält. Ein Individuum entspricht einem Lösungskanidaten. Die durch die genetischen Operatoren erzeugten Individuen werden Nachkommen oder Kinder genannt. Eine Iteration des Verfahrens heißt entsprechend dem biologischen Vorbild Generation. Weitere Begriffsdefinitionen können in der VDI-Richtlinie VDI/VDE 3550[8] gefunden werden.

In der Praxis könnte z. B. die Form einer Autotür so optimiert werden, dass der aerodynamische Widerstand minimal wird. Die Eigenschaften einer potenziellen Lösung werden dabei im Rechner als Genom gespeichert. Häufige Problemrepräsentationen sind Genome aus binären oder reellen Zahlen oder eine Reihenfolge bekannter Elemente (bei kombinatorischen Problemen, z. B. Travelling Salesman).

Die starken Vereinfachungen, die im Vergleich zur Evolution getroffen werden, stellen ein Problem in Bezug auf die Erforschung evolutionsbiologischer Fragestellungen mit EA dar. Ergebnisse können nicht einfach auf die komplexere Natur übertragen werden.

Ablauf

Das grobe Verfahren evolutionärer Algorithmen besteht meist aus einer Initialisierung und einer Generationsschleife, die solange durchlaufen wird, bis ein Abbruchkriterium erfüllt ist:[9]

Initialisierung: Die erste Generation von Lösungskandidaten wird (meist zufällig) erzeugt.
Evaluation: Jedem Lösungskandidaten der Generation wird entsprechend seiner Güte ein Wert der Fitnessfunktion zugewiesen.
Durchlaufe die folgenden Schritte, bis ein Abbruchkriterium erfüllt ist:
1. Selektion: Auswahl von Individuen meist basierend auf ihrer Fitness, die die Eltern für die Rekombination bilden
2. Rekombination: Erzeugung von Nachkommen durch zufällige Kombination der Genome der Eltern
3. Mutation: Zufällige Veränderung aller oder eines Teils der Nachkommen
4. Evaluation: Jedem Nachkommen wird entsprechend seiner Güte ein Wert der Fitnessfunktion zugewiesen.
5. Selektion: Bestimmung einer neuen Generation aus der alten und/oder den in dieser Generation gebildeten Nachkommen

Die verschiedenen EA weichen in der Auswahl der Operatoren (Rekombination, Selektion, …) voneinander ab. So kann man beispielsweise die Schritte Rekombination – Mutation – Evaluation pro Elternpaar mehrmals ausführen, um pro Paarung mehr als zwei Nachkommen zu erzeugen. Oder es werden in Abweichung vom biologischen Vorbild Klone eines Elters erzeugt und mutiert.[7] EAs unterscheiden sich außerdem in verschiedenen Problemrepräsentationen, der entsprechenden Fitnessfunktion oder zusätzlichen Schritten. Rekombination muss dabei nicht zwangsläufig stattfinden, da die Individuen sich auch asexuell fortpflanzen können. EA werden oft mit künstlichen neuronalen Netzen oder lokaler Suche kombiniert, was dann häufig zu memetischen Algorithmen führt. Je nach vorliegender Anwendung ergeben sich Vor- und Nachteile in Bezug auf spezielle Operatoren oder Konzepte.

Bestandteile

Evolutionäre Algorithmen unterscheiden sich untereinander vor allem in der jeweiligen genetischen Repräsentation, der Fitnessfunktion und den genutzten genetischen Operatoren: Mutation, Rekombination und Selektion.

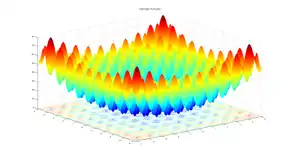
Die Rastrigin-Funktion ist eine multimodale Funktion, da sie viele lokale Extrema aufweist. Dies stellt einen Nachteil für den Rekombinationsoperator dar.

Mutation und Rekombination sind die Suchoperatoren evolutionärer Algorithmen, mit denen der Suchraum erkundet wird. Ihre Anwendung auf Lösungskandidaten kann keine Verbesserung garantieren,[10] allerdings erhält der Suchprozess durch die Selektion eine Richtung, die bei erfolgreicher Konzeption zum globalen Optimum führt. Während mit dem Mutationsoperator völlig neue Bereiche des Suchraums erschlossen werden können, ermöglicht die Rekombination vor allem die Zusammenführung erfolgreicher Teillösungen oder Schemata bei den klassischen genetischen Algorithmen (Building-Block-Hypothese). Eine erfolgreiche Suche basiert also auf der Kombination beider Suchoperatoren. Der Erfolg eines Rekombinationsoperators hängt von der Beschaffenheit der Fitnesslandschaft ab. Je mehr lokale Optima die Fitnesslandschaft aufweist, desto wahrscheinlicher erzeugt die Rekombination aus zwei Individuen, die sich auf einem lokalen Optimum befinden, einen Nachfahren im Tal dazwischen. Mutationen sind von dieser Eigenschaft der Fitnesslandschaft nahezu unabhängig.[11]

Der Entwurf der verschiedenen Komponenten bestimmt, wie sich der evolutionäre Algorithmus bei der Optimierung des gegebenen Problems in Bezug auf Konvergenzverhalten, benötigte Rechenzeit und die Erschließung des Problemraums[12] verhält. Insbesondere müssen die genetischen Operatoren sorgfältig auf die zugrunde liegende Repräsentation abgestimmt sein, sodass sowohl die bekannten, guten Regionen des Problemraums genutzt, als auch die unbekannten Regionen erkundet werden können.[13] Dabei spielen die Beziehungen zwischen Such- und Problemraum eine Rolle. Im einfachsten Fall entspricht der Suchraum dem Problemraum (direkte Problemrepräsentation).

Theoretische Grundlagen

No-free-Lunch-Theorem

Das No-free-Lunch-Theorem der Optimierung besagt, dass alle Optimierungsstrategien gleich effektiv sind, wenn die Menge aller Optimierungsprobleme betrachtet wird. Unter der gleichen Voraussetzung ist auch kein evolutionärer Algorithmus grundsätzlich besser als ein anderer. Dies kann nur dann der Fall sein, wenn die Menge aller Probleme eingeschränkt wird. Genau das wird in der Praxis auch zwangsläufig getan. Ein EA muss also Problemwissen ausnutzen (z. B. durch die Wahl einer bestimmten Mutationsstärke). Werden also zwei EA verglichen, dann wird diese Einschränkung impliziert. Darüber hinaus kann eine EA Problemwissen nutzen, indem z. B. ein Teil der Startpopulation nicht zufällig generiert wird, sondern einige Individuen durch Heuristiken oder andere Verfahren erzeugt werden.[14] Eine weitere Möglichkeit besteht darin, geeignete Heuristiken, lokale Suchverfahren oder andere problembezogene Verfahren bei der Erzeugung der Nachkommen zu beteiligen. Diese Form der Erweiterung eines EAs ist auch als Memetischer Algorithmus bekannt. Beide Erweiterungen spielen bei praktischen Anwendungen eine große Rolle, da sie den Suchprozess beschleunigen und robuster machen können.[15]

Konvergenz

Für EAs, bei denen das beste Individuum der Elterngeneration und ihre Nachkommen pro Generation zur Bildung der Folgegeneration herangezogen wird (sogenannte elitäre EAs), gibt es einen allgemeinen Konvergenzbeweis unter der Voraussetzung, dass ein Optimum existiert. Ohne Beschränkung der Allgemeinheit wird für den Beweis von einer Maximumsuche ausgegangen:

Aus der Eigenschaft elitärer Nachkommensakzeptanz folgt, dass pro Generation k mit einer Wahrscheinlichkeit P > 0 eine Verbesserung der Fitness 𝑭 des jeweils besten Individuums 𝒙′ auftreten wird. Also:

𝑭(𝒙′_𝟏) ≤ 𝑭(𝒙′_𝟐) ≤ 𝑭(𝒙′_𝟑) ≤ ⋯ ≤ 𝑭(𝒙′_𝒌) ≤ ⋯

D. h., die Fitnesswerte stellen eine monoton nicht fallende Zahlenfolge dar, die wegen der Existenz des Optimums beschränkt ist. Daraus folgt die Konvergenz der Zahlenfolge gegen das Optimum.

Da der Beweis keinerlei Aussage über die Konvergenzgeschwindigkeit macht, hilft er bei der praktischen Anwendung von EAs wenig. Aber er begründet die Empfehlung, elitäre EAs zu verwenden. Bei Verwendung des üblichen panmiktischen Populationsmodells neigen elitäre EAs jedoch stärker zur vorzeitigen Konvergenz als nichtelitäre. Bei einem panmiktischen Populationsmodell ist die Partnerwahl (Schritt 3.1 Selektion im Ablaufdiagramm) so gestaltet, dass jedes Individuum der gesamten Population als Partner in Frage kommt. Das generelle Risiko zur vorzeitigen Konvergenz von panmiktischen EAs kann durch geeignete Populationsmodelle deutlich verringert werden.[16][17]

Schematheorem

Das Schematheorem von John H. Holland wird allgemein als Erklärung des Erfolgs von einem Grundtyp evolutionärer Algorithmen, nämlich den klassischen genetischen Algorithmen, gesehen. Es besagt vereinfacht, dass sich kurze Bitmuster mit überdurchschnittlicher Fitness schnell in einer Generation ausbreiten, die durch einen genetischen Algorithmus evolviert wird. So können Aussagen über den langfristigen Erfolg eines genetischen Algorithmus getroffen werden.

Virtuelle Alphabete

Mit der Theorie der virtuellen Alphabete zeigte David E. Goldberg 1990, dass durch eine Repräsentation mit reellen Zahlen ein EA, der klassische Rekombinationsoperatoren (z. B. uniformes oder n-Punkt Crossover) nutzt, bestimmte Bereiche des Suchraums nicht erreichen kann,[18] im Gegensatz zu einer Repräsentation mit binären Zahlen. Daraus ergibt sich, dass EA mit reeller Repräsentation arithmetische Operatoren zur Rekombination nutzen müssen (z. B. arithmetisches Mittel oder die intermediäre Rekombination). Mit geeigneten Operatoren sind reellwertige Repräsentationen entgegen der früheren Meinung effektiver als binäre.[18][19]

Anwendungsgebiete

Die Bereiche, in denen evolutionäre Algorithmen praktisch eingesetzt werden, sind nahezu unbegrenzt[20][21] und reichen von der Industrie und Technik,[22][23] über Forschung bis zur Kunst (evolutionäre Kunst). Die Anwendung eines evolutionären Algorithmus erfordert vom unerfahrenen Anwender ein gewisses Maß an Umdenken, da die Herangehensweise an eine Aufgabenstellung mit Hilfe eines Suchalgorithmus anders ist als bei traditionellen exakten Verfahren und eher nicht zum Curriculum von Ingenieuren oder anderen Fachrichtungen gehört. Es gibt daher einige Publikationen, die den Anfänger als Zielgruppe haben und ihm oder ihr dabei helfen wollen, Anfängerfehler zu vermeiden und ein Anwendungsprojekt zum Erfolg zu führen.[24][25][26] Dazu gehört auch die Klärung der grundlegenden Frage, wann man einen EA zur Lösung einer Aufgabenstellung anwenden soll und wann besser nicht.[24] Die Konferenzserie Applications of Evolutionary Computation kann einen Überblick über die vielfältigen Anwendungen geben und dabei unterstützen, Veröffentlichungen zur eigenen Problemstellung zu finden.[20]

Wirtschaft

EA werden zur Verifikation und Optimierung von Prototypen eingesetzt. Zum Beispiel werden die Geschwindigkeit von Mikroprozessoren, der Stromverbrauch von Mobiltelefonen oder die Wiederverwendbarkeit von Produkten (Recycling) optimiert.[27] Auch bei dem Entwurf von Telekommunikationsnetzen, Infrastruktur allgemein oder Sensornetzen. In der Finanzwelt werden mit EA Aktienmärkte analysiert, spieltheoretische Analysen oder agentenbasierte Simulationen entworfen[28] und Portfolios für maximalen Gewinn und minimales Risiko optimiert.[29] Sogar zur Optimierung von landwirtschaftlichen Betrieben werden sie genutzt, um langjährige Auswirkungen zu testen, Managementstrategien zu entwickeln oder praktisch nicht ausführbare Experimente zu simulieren.[30] Ein weiteres großes Anwendungsgebiet ist Scheduling,[5] Designoptimierung[6][31] oder andere Engineering-Aufgaben.[22][23] Zum Problemfeld der Schedulingaufgaben gehören neben den klassischen Produktionsplanungsaufgaben,[32] Job-Scheduling in Rechnernetzen,[33][23] Stundentafelerstellung[34][35] oder die Einsatzplanung von Energieerzeugern und Verbrauchern in Smart Grids.[23][36]

Forschung

Vor allem in der Molekularbiologie, wo enorme Datenmengen (Big Data) anfallen und Zusammenhänge nicht ohne Computerunterstützung erkannt werden können, werden mit evolutionären Algorithmen Sequenzanalyse, Sequenzalignment, die Erstellung phylogenetischer Bäume, Proteinstrukturvorhersage, Suche nach codierenden Bereichen oder die Visualisierung umfangreicher Daten[37] betrieben.

EA werden benutzt, um künstliche neuronale Netze aufzubauen, ein populärer Algorithmus ist NEAT. Robert Axelrods Versuch, mittels genetischer Algorithmen geeignete Strategien für das iterierte Gefangenendilemma zu finden, gab den Anstoß zur Entwicklung des Konzepts der evolutionären Spieltheorie.[38] Aufgrund ihrer Populationsbasiertheit können evolutionäre Algorithmen auch in der agentenbasierten Modellierung sozialer oder ökonomischer Systeme eingesetzt werden.

In der Spektroskopie werden genetische Algorithmen genutzt, um vieldimensionale Optimierungsprobleme zu lösen.[39] Hierbei wird ein experimentelles Spektrum, zu dessen Beschreibung eine große Anzahl an Parametern benötigt werden, mit Hilfe evolutionärer Strategien an ein berechnetes Modellspektrum angepasst. Als Fitnessfunktion wird oft die Kreuzkorrelation zwischen experimentellem und theoretischem Spektrum angewandt.

Kunst und Musik

Mit der Hilfe evolutionärer Algorithmen können komplexe Strukturen oder Tonfolgen entworfen werden, die auf Menschen ästhetisch wirken. Dies geschieht teils automatisiert und oft mit menschlicher Interaktion, wobei Menschen dem EA die Entscheidung abnehmen, was sie als schön empfinden.

Geschichte

George Friedman entwarf 1956 für seine Masterarbeit an der University of California, Los Angeles eine Maschine, die mit dem Prinzip der natürlichen Selektion Schaltkreise entwickeln sollte, allerdings wurde diese Maschine nie gebaut.[2] Auch künstliches Leben wurde früh mit EA erforscht. Der Italiener Nils Barricelli (1912–1993) entwickelte 1954 ein Konzept, bei dem durch Zahlen repräsentierte Wesen auf einem zweidimensionalen Gitter "leben" und durch Mutation und Reproduktion zu neuen Generation geformt werden. Er zeigte, dass sich selbstreplikative Strukturen bilden, also Strukturen, die sich selbst in die nächste Generation kopieren. Bezüglich maschinellen Lernens schrieb der britische Informatiker Alan Turing schon 1950:

„Man muss mit dem Unterrichten einer Maschine herumexperimentieren und schauen, wie gut sie lernt. […] Es gibt einen offensichtlichen Zusammenhang zwischen diesem Prozess und Evolution […] Man darf allerdings hoffen, dass dieser Prozess schneller abläuft.“

– Alan Turing: Computing Machinery and Intelligence[40]

Anfang der 1950er schlug der britische Statistiker George Box vor, die Produktion in Chemiefabriken zu optimieren, indem mit massivem Trial and Error Parameter wie Temperatur oder chemische Zusammensetzungen variiert und die potenziellen Verbesserungen per Hand ausgewertet werden, um danach mit den gefundenen Verbesserungen wieder zu variieren. Obwohl die Entscheidungsträger zuerst nicht davon begeistert waren, an einer laufenden Produktion zu experimentieren, wurde das Konzept, das Box Evolutionary Operation taufte, bis Anfang der 1960er in mehreren Chemiefabriken zur Steigerung der Produktivität genutzt.[3] Viele praktische Probleme ging man in der Folge mit evolutionären Algorithmen an, es bildeten sich vor allem die Evolutionsstrategie in Europa (Ingo Rechenberg[41] und Hans-Paul Schwefel[42]) und der genetische Algorithmus (John H. Holland[43]) in den USA heraus, wobei Letzterer der bis heute populärste Ansatz ist und der Begriff genetischer Algorithmus oft pauschalisierend für alle EA genutzt wird. Dies hat aber keine praktische Bedeutung für die Auswahl eines konkreten Konzeptes.[2] Spätestens mit der rasant steigenden Verfügbarkeit von Rechenkraft fanden sich evolutionäre Algorithmen in allen erdenklichen Bereichen wieder, wo sie zur Optimierung und Suche eingesetzt wurden. Insbesondere auch in der Kunst und Musik, sowie in der Erforschung von künstlichem Leben (Avida).

Heute sind nicht nur die ursprünglichen Konzepte stark miteinander verwachsen, sondern auch viele andere Ansätze und Mischkonzepte entstanden. EA stellen wichtige Werkzeuge für Industrie und Forschung dar.

Typen evolutionärer Algorithmen

Durch die Problemstellung des Optimierungsproblems sind eine Zielfunktion sowie ein Problemraum, der potenzielle Lösungen enthält, gegeben. Der Unterschied zwischen dem Problemraum der Anwendung und dem Suchraum des Algorithmus besteht darin, dass ein EA eine Lösung anders darstellen kann, um sie besser zu verarbeiten und später wieder in ursprünglicher Form auszugeben (Genotyp-Phänotyp-Mapping, künstliche Embryogenese). Dies bietet sich vor allem dann an, wenn die Darstellung einer möglichen Lösung deutlich vereinfacht werden kann und nicht in ihrer Komplexität im Speicher verarbeitet werden muss. Verschiedene evolutionäre Algorithmen unterscheiden sich vornehmlich in den folgenden Eigenschaften (vergleiche auch das einleitende Ablaufschema):

Suchraum (z. B. Binärzahlen, reelle Zahlen, Baumstrukturen)
Suchoperatoren (z. B. Mutation und Rekombination)
Fitnesszuweisung und Selektion auf Basis der Zielfunktion
Art und Weise, in der vorherige Generationen in die Selektion mit einbezogen werden (Elterngeneration ein-/ausschließen)
Beziehung zwischen dem Suchraum und dem Problemraum (Genotyp-Phänotyp-Mapping)

Klassische Varianten

Die vier historisch zuerst entstandenen Verfahren sind heute in der Form nicht mehr zu unterscheiden, insbesondere werden oft die Namen einzelner Typen als Synonym für das gesamte Gebiet der evolutionären Algorithmen genutzt. Dazu kommt, dass es heute eine Fülle weiterer Verfahren und unüberschaubar viele Kombinationen gibt, für die keine einheitliche Benennung existiert. In der folgenden Darstellung werden die klassischen Konzepte in der historischen Form beschrieben. Ein guter und theoretisch fundierter Vergleich zwischen den klassischen bit-codierten und den reell-codierten GAs, der ES und der EP kann z. B. bei Whitley gefunden werden.[44]

Genetische Algorithmen (GA)

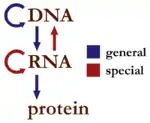
Ausprägung des Genotyps in einer Zelle

Genetische Algorithmen wurden vor allem durch die Arbeiten John H. Hollands berühmt. Sie nutzen binäre Problemrepräsentation und benötigen deshalb meist ein Genotyp-Phänotyp-Mapping. Das bedeutet, dass binär repräsentierte Lösungskandidaten zuerst umgewandelt werden müssen, um mit der Fitnessfunktion evaluiert werden zu können. Wegen dieser Eigenschaft sind sie dem biologischen Vorbild von allen evolutionären Algorithmen am nächsten. Das Erbgut natürlicher Organismen ist ähnlich binären Zahlen in vier Nukleinsäuren codiert. Auf dieser Basis geschehen natürliche Mutation und Rekombination. Das Erscheinungsbild (Phänotyp) ist aber nicht das Erbgut selbst, sondern entsteht aus diesem durch einen vielschrittigen Prozess. Das Prinzip Genotyp-Phänotyp-Mapping verläuft in vereinfachter Form analog. Die binäre Repräsentation eignet sich zur schnellen Verarbeitung in Computern. Im Laufe der Forschung im Gebiet der EA hat sich dies aber nicht als klarer Vorteil gegenüber anderen Verfahren[45][44] und Problemrepräsentationen[46][47] erwiesen.

Die Auswahl der sich fortpflanzenden Individuen erfolgt bei GA mit fitnessproportionaler Selektion, die Fortpflanzung selbst durch n-Punkt-Crossover. Auch die Rekombination von mehr als zwei Elterngenomen ist möglich und führt in manchen Fällen zu besseren Ergebnissen.[48] Die Mutation bei GA kann man sich anschaulich gut vorstellen, da die Genome aus einzelnen Bits bestehen, die invertiert, dupliziert oder gelöscht werden können (auch ganze Sequenzen). Eine theoretische Untersuchung des Konvergenzverhaltens Genetischer Algorithmen liefert das Schematheorem von John H. Holland.

Evolutionsstrategien (ES)

Evolutionsstrategien[42][41] nutzen direkte Problemrepräsentationen (z. B. reelle Zahlen). Problem- und Suchraum sind also identisch. Das hat bei komplexen Problemen zur Folge, dass die Evolutionsstrategie nicht den gesamten Problemraum erkunden kann, wenn klassische Crossoveroperatoren benutzt werden (virtuelle Alphabete). ES nutzen vorrangig Mutation als Suchoperator und in manchen Fällen gar keine Rekombination. Die Mutation stellt eine Addition eines normalverteilten Wertes dar, wobei die Varianz (Mutationsstärke) nicht konstant ist. Da der Algorithmus mit zunehmender Lösungsqualität konvergiert (Schematheorem), ist es vorteilhaft, die Varianz anzupassen. So kann gewährleistet werden, dass die ES in immer feineren Schritten ihr Ziel sucht. Für die Anpassung haben sich zwei Methoden etabliert.

Adaptive Anpassung (1/5-Erfolgsregel[49]): Die 1/5-Erfolgsregel besagt, dass der Quotient aus den erfolgreichen Mutationen (also Mutationen, die eine Verbesserung der Anpassung bewirken) zu allen Mutationen etwa ein Fünftel betragen sollte. Ist der Quotient größer, so sollte die Varianz der Mutationen erhöht werden, bei einem kleineren Quotienten sollte sie verringert werden.
Selbstadaptivität: Jedes Individuum hat ein zusätzliches Gen für die Mutationsstärke selbst. Dies ist zwar nicht in der Biologie möglich, aber die Evolution im Rechner findet eine geeignete Varianz auf diese Weise ohne Einschränkung des Menschen.

Genetische Programmierung (GP)

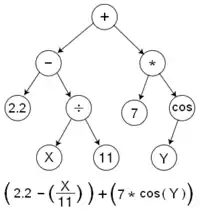
Darstellung einer Funktion als Ausdrucksbaum. Teilbäume können umgehängt, geändert oder gelöscht (Mutation) und komplette Bäume kombiniert (Rekombination) werden.

Das Ziel der genetischen Programmierung ist die Erzeugung von Strukturen, die eine bestimmte Eingabe in eine festgelegte Ausgabe umwandeln sollen (Computerprogramme, Schaltkreise oder mathematische Funktionen). Die Lösungskandidaten werden durch Bäume repräsentiert.

Beim Problem der symbolischen Regression wird eine bestimmte Funktion $X\to Y$ gesucht (z. B. ein Polynom wie $4x^{4}-3x^{2}+17$ ). Gegeben sind Paare mit je einem Wert aus $X$ und dem zugehörigen Wert aus $Y$ . Es ist also bekannt, wie die gesuchte Funktion Werte abbildet. Mit GP werden Baumstrukturen evolviert, die die symbolische Funktion meist exakt nachbilden.[50]

Eine grundlegende Arbeit zur Genetischen Programmierung verfasste John Koza. Er erkannte auch die Möglichkeit, symbolische Regression mit GP zu lösen. In der Erforschung von GP wurde dieses Problem oft als Benchmarktest genutzt.

Evolutionäre Programmierung (EP)

Ähnlich wie bei der GP werden Strukturen wie Computerprogramme gesucht, die aber nicht durch Bäume, sondern durch endliche Automaten repräsentiert werden. Nur die numerischen Eigenschaften der Automaten werden variiert, ihre Struktur ist fest. Gesucht wird ausschließlich über Mutation, Rekombination findet nicht statt. Einzelne Individuen werden sozusagen als unterschiedliche Spezies betrachtet. Evolutionäre Programmierung wurde nach ihrer Entstehung wenig weiterentwickelt.

Siehe auch

Literatur

Evolutionäre Algorithmen allgemein

Ingrid Gerdes, Frank Klawonn, Rudolf Kruse: Evolutionäre Algorithmen: genetische Algorithmen – Strategien und Optimierungsverfahren – Beispielanwendungen. Vieweg, Wiesbaden 2004, ISBN 3-528-05570-7.
Volker Nissen: Einführung in evolutionäre Algorithmen: Optimierung nach dem Vorbild der Evolution. Vieweg, Braunschweig 1997, ISBN 3-528-05499-9.
Hartmut Pohlheim: Evolutionäre Algorithmen: Verfahren, Operatoren und Hinweise für die Praxis. Springer, Berlin 1999, ISBN 3-540-66413-0.
Karsten Weicker: Evolutionäre Algorithmen. Springer Vieweg, Wiesbaden, 2015. ISBN 978-3-658-09957-2. doi:10.1007/978-3-658-09958-9
Agoston E. Eiben, Jim E. Smith: Introduction to Evolutionary Computing. Springer, Berlin, Heidelberg, 2003. doi:10.1007/978-3-662-44874-8
Kenneth A. de Jong: Evolutionary Computation: A Unified Approach. MIT Press, Cambridge, MA 2006, ISBN 0-262-04194-4.
VDI/VDE-Richtlinie 3550, Blatt 3: Evolutionäre Algorithmen – Begriffe und Definitionen. Weißdruck, (in Deutsch und Englisch) Beuth-Verlag, Berlin, 2003.
VDI/VDE-Richtlinie 6224, Blatt 1: Bionische Optimierung – Evolutionäre Algorithmen in der Anwendung. Weißdruck, (in Deutsch und Englisch), Beuth-Verlag, Berlin, 2012.

Genetische Algorithmen

David E. Goldberg: Genetic Algorithms in Search, Optimization, and Machine Learning. Addison-Wesley, 1989, ISBN 0-201-15767-5.
J. Heistermann: Genetische Algorithmen. Teubner, Stuttgart 1994. doi:10.1007/978-3-322-99633-6
Melanie Mitchell: An Introduction to Genetic Algorithms. MIT Press, Cambridge MA 1996. ISBN 978-0-262-63185-3

Evolutionsstrategien

Ingo Rechenberg: Cybernetic Solution Path of an Experimental Problem (1965). In: D.B. Fogel (Hrsg.): Evolutionary Computation – The Fossil Record. IEEE Press, 1998, ISBN 0-7803-3481-7.
Ingo Rechenberg: Evolutionsstrategie. Optimierung technischer Systeme nach Prinzipien der biologischen Evolution. Frommann Holzboog, 1973, ISBN 3-7728-0373-3 (Diss. von 1970).
Ingo Rechenberg, Evolutionsstrategie ’94. Frommann Holzboog, 1994, ISBN 3-7728-1642-8.
Hans-Paul Schwefel: Evolution and Optimum Seeking. Wiley & Sons, New York 1995, ISBN 0-471-57148-2.
Hans-Georg Beyer: The Theory of Evolution Strategies. Springer, Berlin / Heidelberg / New York 1998, ISBN 3-540-67297-4.
Hannes Geyer et al.: Vergleich zwischen klassischen und verschachtelten Evolutionsstrategien am Beispiel einer nichtlinearen Regression an Oberflächenspannungen in R². Interner Bericht CI-66/99 des Sonderforschungsbereichs 531: „Design und Management komplexer technischer Prozesse und Systeme mit Methoden der Computational Intelligence“, Dortmund 1999, PDF

Genetische Programmierung

John R. Koza: Genetic Programming. On the Programming of Computers by Means of Natural Selection. The MIT Press, 1992, ISBN 0-262-11170-5.
Wolfgang Banzhaf, Peter Nordin, Robert E. Keller, Frank D. Francone: Genetic Programming – An Introduction. Morgan Kaufmann, San Francisco, CA, USA, 1997. ISBN 3-920993-58-6
William B. Langdon, Riccardo Poli: Foundations of Genetic Programming. Springer, 2002, ISBN 3-540-42451-2.
Riccardo Poli, William B. Langdon, Nicholas Freitag McPhee: A Field Guide to Genetic Programming. Lulu.com, 2008.

Evolutionäre Programmierung

Laurence J. Fogel, Alvin J. Owens, Michael John Walsh: Artificial Intelligence through Simulated Evolution. John Wiley, 1966. doi:10.1109/9780470544600.ch7
David. B. Fogel: Blondie24: Playing at the Edge of AI. Morgan Kaufmann Publishers, San Francisco CA 2002, ISBN 1-55860-783-8.

Weblinks

Evolutionäre Algorithmen allgemein

Thomas Weise: Global Optimization Algorithms - Theory and Application , 2009. (PDF; 13,14 MB)
EvA2 (Java), umfassendes Framework für EA und heuristische Optimierung mit GUI.

Genetische Algorithmen

Genetische Algorithmen. Wikiversity-Kurs.
JGAP – Freies Java Framework zur Implementierung genetischer Algorithmen, unterstützt auch die Genetische Programmierung; sehr viele Unit Tests zur Qualitätssicherung, umfangreiche Javadoc-Dokumentation
EvoJ – Kleines aber effektives und verbreitbares Java Framework für genetischer Algorithmen.
Jenetics – in Java 11 geschriebener, genetischer Algorithmus und nutzt die Java Stream API zur Evaluierung der einzelnen Generationen.
HeuristicLab – Freies .NET Environment für heuristische Optimierung (genetische Algorithmen, Evolutionsstrategien, Nachbarschaftssuche etc.)
Boxcar2D, ein genetischer Algorithmus, der ein 2-dimensionales Fahrzeug konstruiert, um ein Gelände zu überwinden

Hybrid-Algorithmen

Geneva („Grid-enabled evolutionary algorithms“), eine freie Bibliothek (Affero GPLv3) zur Optimierung mit Evolutionsstrategien, Genetischen- und Schwarmalgorithmen sowie Simulated Annealing und Parameter Scans. Unterstützt Problembeschreibungen mit gemischten Parametersätzen sowie die Optimierung in Clustern sowie Grid und Cloud

Einzelnachweise

J.D. Lohn, D.S. Linden, G.S. Hornby, W.F. Kraus: Evolutionary design of an X-band antenna for NASA's Space Technology 5 mission. In: Antennas and Propagation Society International Symposium. Vol.3,IEEE , 20-25 June 2004, S. 2313–2316
Peter Bentley, David Corne: Creative Evolutionary Systems. Morgan Kaufmann, San Francisco, CA, 2001, S. 10. ISBN 978-1-55860-673-9
David B. Fogel: Evolutionary Computation: Toward a New Philosophy of Machine Intelligence. Wiley, New York, S. 59, 2005. ISBN 978-0-471-66951-7
Cecilia Di Chio et al.: Applications of Evolutionary Computation: EvoApplications 2012. LNCS 7248, Springer, Berlin, Heidelberg, 2012. doi:10.1007/978-3-642-29178-4
Keshav P. Dahal, Kay Chen Tan, Peter I. Cowling (Hrsg.): Evolutionary Scheduling. SCI, Nr. 49. Springer, Berlin, Heidelberg 2007, ISBN 978-3-540-48582-7, doi:10.1007/978-3-540-48584-1 (springer.com [abgerufen am 8. Februar 2022]).
Ian C. Parmee: Strategies for the Integration of Evolutionary/Adaptive Search with the Engineering Design Process. In: Dipankar Dasgupta, Zbigniew Michalewicz (Hrsg.): Evolutionary Algorithms in Engineering Applications. Springer Berlin Heidelberg, Berlin, Heidelberg 1997, ISBN 978-3-642-08282-5, S. 453–477, doi:10.1007/978-3-662-03423-1_25 (springer.com [abgerufen am 8. Februar 2022]).
Christian Blume, Wilfried Jakob: GLEAM - General Learning Evolutionary Algorithm and Method: Ein Evolutionärer Algorithmus und seine Anwendungen. In: Schriftenreihe des Instituts für Angewandte Informatik – Automatisierungstechnik. Band 32. KIT Scientific Publishing, Karlsruhe 2009, ISBN 978-3-86644-436-2, doi:10.5445/KSP/1000013553.
VDI/VDE-Richtlinie 3550, Blatt 3: Evolutionäre Algorithmen - Begriffe und Definitionen. Weißdruck (in Deutsch und Englisch) Beuth-Verlag, Berlin, 2003.
Karsten Weicker: Evolutionäre Algorithmen. S. 25. Springer Vieweg, Wiesbaden, 2015. doi:10.1007/978-3-658-09958-9
Mitsuo Gen, Runwei Cheng: Genetic Algorithms and Engineering Optimization. Wiley, New York, 2000, S. 8. ISBN 978-0-471-31531-5. doi:10.1002/9780470172261
William M. Spears: The Role of Mutation and Recombination in Evolutionary Algorithms. Springer, Berlin, Heidelberg, 2000, S. 225f. doi:10.1007/978-3-662-04199-4
Bill Worzel, Terence Soule, Rick Riolo: Genetic Programming Theory and Practice VI. Springer, Berlin, Heidelberg, 2009, S. 62. doi:10.1007/978-0-387-87623-8
Oscar Cordón, Francisco Herrera, Frank Hoffmann, Luis Magdalena: Genetic Fuzzy Systems: Evolutionary Tuning and Learning of Fuzzy Knowledge Bases. World Scientific Publishing, Singapore, 2002, S. 95. doi:10.1142/4177
Ralf Mikut, Frank Hendrich: Produktionsreihenfolgeplanung in Ringwalzwerken mit wissensbasierten und evolutionären Methoden. In: Automatisierungstechnik. Band 46, Nr. 1, Januar 1998, ISSN 2196-677X, S. 15–21, doi:10.1524/auto.1998.46.1.15 (degruyter.com [abgerufen am 7. Januar 2022]).
Ferrante Neri, Carlos Cotta, Pablo Moscato (Eds.): Handbook of Memetic Algorithms (= Studies in Computational Intelligence. Nr. 379). Springer, Berlin, Heidelberg 2012, ISBN 978-3-642-26942-4, doi:10.1007/978-3-642-23247-3.
Martina Gorges-Schleuter: A comparative study of global and local selection in evolution strategies. In: Parallel Problem Solving from Nature — PPSN V. Band 1498. Springer Berlin Heidelberg, Berlin, Heidelberg 1998, ISBN 978-3-540-65078-2, S. 367–377, doi:10.1007/bfb0056879 (springer.com [abgerufen am 14. Januar 2022]).
Cellular Genetic Algorithms (= Operations Research/Computer Science Interfaces Series. Band 42). Springer US, Boston, MA 2008, ISBN 978-0-387-77609-5, doi:10.1007/978-0-387-77610-1 (springer.com [abgerufen am 14. Januar 2022]).
J. Stender, E. Hillebrand, J. Kingdon: Genetic Algorithms in Optimisation, Simulation and Modelling. IOS Press, Amsterdam, 1994, S. 70. ISBN 978-90-5199-180-2
Zbigniew Michalewicz: Genetic Algorithms + Data Structures = Evolution Programs. Third, revised and Extended edition Auflage. Springer, Berlin, Heidelberg 1996, ISBN 978-3-662-03315-9.
International Conference on the Applications of Evolutionary Computation,. Die Konferenz ist Teil der Evo*-Serie. Die Conference Proceedings erscheinen im Springer Verlag: https://link.springer.com/conference/evoapplications, abgerufen am 8. Februar 2022 (englisch).
Hitoshi Iba, Nasimul Noman: New Frontier in Evolutionary Algorithms: Theory and Applications. IMPERIAL COLLEGE PRESS, 2011, ISBN 978-1-84816-681-3, doi:10.1142/p769 (worldscientific.com [abgerufen am 8. Februar 2022]).
Dipankar Dasgupta, Zbigniew Michalewicz (Hrsg.): Evolutionary Algorithms in Engineering Applications. Springer, Berlin, Heidelberg 1997, ISBN 978-3-642-08282-5, doi:10.1007/978-3-662-03423-1 (springer.com [abgerufen am 8. Februar 2022]).
Adam Slowik, Halina Kwasnicka: Evolutionary algorithms and their applications to engineering problems. In: Neural Computing and Applications. Band 32, Nr. 16, August 2020, ISSN 0941-0643, S. 12363–12379, doi:10.1007/s00521-020-04832-8 (springer.com [abgerufen am 8. Februar 2022]).
Wilfried Jakob: Applying Evolutionary Algorithms Successfully - A Guide Gained from Real-world Applications. KIT Scientific Working Papers, Nr. 170. KIT Scientific Publishing, 2021, ISSN 2194-1629, doi:10.5445/IR/1000135763, arxiv:2107.11300 (kit.edu).
Karsten Weicker: Evolutionäre Algorithmen. Springer Fachmedien Wiesbaden, Wiesbaden 2015, ISBN 978-3-658-09957-2, doi:10.1007/978-3-658-09958-9 (springer.com [abgerufen am 8. Februar 2022]).
Hartmut Pohlheim: Evolutionäre Algorithmen - Verfahren, Operatoren und Hinweise für die Praxis. VDI-Buch. Springer, Berlin, Heidelberg 2000, ISBN 978-3-642-63052-1, doi:10.1007/978-3-642-57137-4 (springer.com [abgerufen am 8. Februar 2022]).
Ernesto Sanchez, Giovanni Squillero, Alberto Tonda: Industrial Applications of Evolutionary Algorithms. Springer, Berlin, Heidelberg, 2012. doi:10.1007/978-3-642-27467-1
Shu-Heng Chen: Evolutionary Computation in Economics and Finance. Physica, Heidelberg, 2002. S. 6. doi:10.1007/978-3-7908-1784-3
Claus Aranha, Hitoshi Iba: Application of a Memetic Algorithm to the Portfolio Optimization Problem. In: Wayne Wobcke, Mengjie Zhang (Hrsg.): Advances in Artificial Intelligence. AI 2008. LNCS 5360. Springer, Berlin, Heidelberg, 2008. doi:10.1007/978-3-540-89378-3_52
David G. Mayer: Evolutionary Algorithms and Agricultural Systems. Springer, Boston, MA, 2002, S. 2. doi:10.1007/978-1-4615-1717-7
Kalyanmoy Deb: GeneAS: A Robust Optimal Design Technique for Mechanical Component Design. In: Dipankar Dasgupta, Zbigniew Michalewicz (Hrsg.): Evolutionary Algorithms in Engineering Applications. Springer Berlin Heidelberg, Berlin, Heidelberg 1997, ISBN 978-3-642-08282-5, S. 497–514, doi:10.1007/978-3-662-03423-1_27 (springer.com [abgerufen am 8. Februar 2022]).
Thomas Bäck, David Fogel, Zbigniew Michalewicz (Hrsg.): Handbook of Evolutionary Computation. 0. Auflage. Oxford University Press / IOP Publishing, New York 1997, ISBN 978-0-367-80248-6, doi:10.1201/9780367802486 (taylorfrancis.com [abgerufen am 8. Februar 2022]).
Wilfried Jakob, Sylvia Strack, Alexander Quinte, Günther Bengel, Karl-Uwe Stucky: Fast Rescheduling of Multiple Workflows to Constrained Heterogeneous Resources Using Multi-Criteria Memetic Computing. In: Algorithms. Band 6, Nr. 2, 22. April 2013, ISSN 1999-4893, S. 245–277, doi:10.3390/a6020245 (mdpi.com [abgerufen am 8. Februar 2022]).
Alberto Colorni, Marco Dorigo, Vittorio Maniezzo: Genetic Algorithms: A New Approach to the Timetable Problem. In: M. Akgül, H.W. Hamacher, S. Tüfekçi (Hrsg.): Combinatorial Optimization. NATO ASI Series (Series F: Computer and Systems Sciences), Nr. 82. Springer, Berlin, Heidelberg 1992, ISBN 978-3-642-77491-1, S. 235–239, doi:10.1007/978-3-642-77489-8_14 (springer.com [abgerufen am 8. Februar 2022]).
B. Paechter, A. Cumming, H. Luchian: The use of local search suggestion lists for improving the solution of timetable problems with evolutionary algorithms. In: Terence C. Fogarty (Hrsg.): Evolutionary computing: AISB Workshop, Brighton, U.K.: selected papers. Springer, Berlin, Heidelberg 1996, ISBN 3-540-61749-3.
Dipankar Dasgupta: Optimal Scheduling of Thermal Power Generation Using Evolutionary Algorithms. In: Dipankar Dasgupta, Zbigniew Michalewicz (Hrsg.): Evolutionary Algorithms in Engineering Applications. Springer, Berlin, Heidelberg 1997, ISBN 978-3-642-08282-5, S. 317–328, doi:10.1007/978-3-662-03423-1_18 (springer.com [abgerufen am 8. Februar 2022]).
Gary Fogel, David Corne: Evolutionary Computation in Bioinformatics. Morgan Kaufmann, 2002. ISBN 978-1-55860-797-2[https://doi.org/10.1016/B978-1-55860-797-2.X5000-8 10.1016/B978-1-55860-797-2.X5000-8]
Robert Axelrod: Die Evolution der Kooperation. Oldenbourg, München 1987; 7. Auflage, 2014. ISBN 978-3-486-59172-9. doi:10.1524/9783486851748
W. Leo Meerts, Michael Schmitt: Application of genetic algorithms in automated assignments of high-resolution spectra. In: International Reviews in Physical Chemistry. Band 25, Nr. 3, 1. Juli 2006, ISSN 0144-235X, S. 353–406, doi:10.1080/01442350600785490.
A. M. Turing: Computing machinery and intelligence. In: Mind, 59, S. 433–460. 1950. loebner.net (Memento des Originals vom 2. Juli 2008 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/loebner.net
Ingo Rechenberg: Evolutionsstrategie – Optimierung technischer Systeme nach Prinzipien der biologischen Evolution (PhD thesis) (German). Frommann-Holzboog, 1973. ISBN 3-7728-0373-3
Hans-Paul Schwefel: Evolution and Optimum Seeking. Sixth-generation computer technology series. John Wiley & Sons, New York 1995, ISBN 0-471-57148-2.
John H. Holland: Adaptation in Natural and Artificial Systems. University of Michigan Press, 1975, ISBN 0-262-58111-6.
Darrell Whitley: An overview of evolutionary algorithms: practical issues and common pitfalls. In: Information and Software Technology. Band 43, Nr. 14, Dezember 2001, S. 817–831, doi:10.1016/S0950-5849(01)00188-4 (elsevier.com [abgerufen am 8. Februar 2022]).
Lukáš Sekanina: Evolvable Components: From Theory to Hardware Implementations. Springer, Berlin, Heidelberg, 2004, S. 27. doi:10.1007/978-3-642-18609-7
Cesary Janikow, Zbigniew Michalewicz: An Experimental Comparison of Binary and Floating Point Representations in Genetic Algorithms. In: Conf. Proc of the Fourth Int. Conf. on Genetic Algorithms (ICGA'91). 1991, S. 31–36 (umsl.edu [PDF]).
Zbigniew Michalewicz: Genetic Algorithms + Data Structures = Evolution Programs. Springer, Berlin, Heidelberg 1996, ISBN 978-3-662-03315-9.
Chuan-Kang Ting: On the Mean Convergence Time of Multi-parent Genetic Algorithms Without Selection. In: Advances in Artificial Life, 2005, ISBN 978-3-540-28848-0, S. 403–412.
Ingo Rechenberg: Evolutionsstrategie. Optimierung technischer Systeme nach Prinzipien der biologischen Evolution. Frommann Holzboog, 1973, ISBN 3-7728-0373-3 (Diss. von 1970), Kapitel 15
Julian F. Miller: Cartesian Genetic Programming. Natural Computing Series. Springer, Berlin, Heidelberg, 2011, S. 63. doi:10.1007/978-3-642-17310-3_2

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] J.D. Lohn, D.S. Linden, G.S. Hornby, W.F. Kraus: Evolutionary design of an X-band antenna for NASA's Space Technology 5 mission. In: Antennas and Propagation Society International Symposium. Vol.3,IEEE , 20-25 June 2004, S. 2313–2316

[George_Friedman-2] Peter Bentley, David Corne: Creative Evolutionary Systems. Morgan Kaufmann, San Francisco, CA, 2001, S. 10. ISBN 978-1-55860-673-9

[Toward_a_New_Philosophy_of_Machine_Intelligence-3] David B. Fogel: Evolutionary Computation: Toward a New Philosophy of Machine Intelligence. Wiley, New York, S. 59, 2005. ISBN 978-0-471-66951-7

[EvoApplications_2012-4] Cecilia Di Chio et al.: Applications of Evolutionary Computation: EvoApplications 2012. LNCS 7248, Springer, Berlin, Heidelberg, 2012. doi:10.1007/978-3-642-29178-4

[:1-5] Keshav P. Dahal, Kay Chen Tan, Peter I. Cowling (Hrsg.): Evolutionary Scheduling. SCI, Nr. 49. Springer, Berlin, Heidelberg 2007, ISBN 978-3-540-48582-7, doi:10.1007/978-3-540-48584-1 (springer.com [abgerufen am 8. Februar 2022]).

[:2-6] Ian C. Parmee: Strategies for the Integration of Evolutionary/Adaptive Search with the Engineering Design Process. In: Dipankar Dasgupta, Zbigniew Michalewicz (Hrsg.): Evolutionary Algorithms in Engineering Applications. Springer Berlin Heidelberg, Berlin, Heidelberg 1997, ISBN 978-3-642-08282-5, S. 453–477, doi:10.1007/978-3-662-03423-1_25 (springer.com [abgerufen am 8. Februar 2022]).

[:0-7] Christian Blume, Wilfried Jakob: GLEAM - General Learning Evolutionary Algorithm and Method: Ein Evolutionärer Algorithmus und seine Anwendungen. In: Schriftenreihe des Instituts für Angewandte Informatik – Automatisierungstechnik. Band 32. KIT Scientific Publishing, Karlsruhe 2009, ISBN 978-3-86644-436-2, doi:10.5445/KSP/1000013553.

[8] VDI/VDE-Richtlinie 3550, Blatt 3: Evolutionäre Algorithmen - Begriffe und Definitionen. Weißdruck (in Deutsch und Englisch) Beuth-Verlag, Berlin, 2003.

[9] Karsten Weicker: Evolutionäre Algorithmen. S. 25. Springer Vieweg, Wiesbaden, 2015. doi:10.1007/978-3-658-09958-9

[10] Mitsuo Gen, Runwei Cheng: Genetic Algorithms and Engineering Optimization. Wiley, New York, 2000, S. 8. ISBN 978-0-471-31531-5. doi:10.1002/9780470172261

[11] William M. Spears: The Role of Mutation and Recombination in Evolutionary Algorithms. Springer, Berlin, Heidelberg, 2000, S. 225f. doi:10.1007/978-3-662-04199-4

[12] Bill Worzel, Terence Soule, Rick Riolo: Genetic Programming Theory and Practice VI. Springer, Berlin, Heidelberg, 2009, S. 62. doi:10.1007/978-0-387-87623-8

[13] Oscar Cordón, Francisco Herrera, Frank Hoffmann, Luis Magdalena: Genetic Fuzzy Systems: Evolutionary Tuning and Learning of Fuzzy Knowledge Bases. World Scientific Publishing, Singapore, 2002, S. 95. doi:10.1142/4177

[14] Ralf Mikut, Frank Hendrich: Produktionsreihenfolgeplanung in Ringwalzwerken mit wissensbasierten und evolutionären Methoden. In: Automatisierungstechnik. Band 46, Nr. 1, Januar 1998, ISSN 2196-677X, S. 15–21, doi:10.1524/auto.1998.46.1.15 (degruyter.com [abgerufen am 7. Januar 2022]).

[15] Ferrante Neri, Carlos Cotta, Pablo Moscato (Eds.): Handbook of Memetic Algorithms (= Studies in Computational Intelligence. Nr. 379). Springer, Berlin, Heidelberg 2012, ISBN 978-3-642-26942-4, doi:10.1007/978-3-642-23247-3.

[16] Martina Gorges-Schleuter: A comparative study of global and local selection in evolution strategies. In: Parallel Problem Solving from Nature — PPSN V. Band 1498. Springer Berlin Heidelberg, Berlin, Heidelberg 1998, ISBN 978-3-540-65078-2, S. 367–377, doi:10.1007/bfb0056879 (springer.com [abgerufen am 14. Januar 2022]).

[17] Cellular Genetic Algorithms (= Operations Research/Computer Science Interfaces Series. Band 42). Springer US, Boston, MA 2008, ISBN 978-0-387-77609-5, doi:10.1007/978-0-387-77610-1 (springer.com [abgerufen am 14. Januar 2022]).

[Stender,_Hillebrand,_Kingdon-18] J. Stender, E. Hillebrand, J. Kingdon: Genetic Algorithms in Optimisation, Simulation and Modelling. IOS Press, Amsterdam, 1994, S. 70. ISBN 978-90-5199-180-2

[19] Zbigniew Michalewicz: Genetic Algorithms + Data Structures = Evolution Programs. Third, revised and Extended edition Auflage. Springer, Berlin, Heidelberg 1996, ISBN 978-3-662-03315-9.

[:3-20] International Conference on the Applications of Evolutionary Computation,. Die Konferenz ist Teil der Evo*-Serie. Die Conference Proceedings erscheinen im Springer Verlag: https://link.springer.com/conference/evoapplications, abgerufen am 8. Februar 2022 (englisch).

[21] Hitoshi Iba, Nasimul Noman: New Frontier in Evolutionary Algorithms: Theory and Applications. IMPERIAL COLLEGE PRESS, 2011, ISBN 978-1-84816-681-3, doi:10.1142/p769 (worldscientific.com [abgerufen am 8. Februar 2022]).

[:4-22] Dipankar Dasgupta, Zbigniew Michalewicz (Hrsg.): Evolutionary Algorithms in Engineering Applications. Springer, Berlin, Heidelberg 1997, ISBN 978-3-642-08282-5, doi:10.1007/978-3-662-03423-1 (springer.com [abgerufen am 8. Februar 2022]).

[:5-23] Adam Slowik, Halina Kwasnicka: Evolutionary algorithms and their applications to engineering problems. In: Neural Computing and Applications. Band 32, Nr. 16, August 2020, ISSN 0941-0643, S. 12363–12379, doi:10.1007/s00521-020-04832-8 (springer.com [abgerufen am 8. Februar 2022]).

[:6-24] Wilfried Jakob: Applying Evolutionary Algorithms Successfully - A Guide Gained from Real-world Applications. KIT Scientific Working Papers, Nr. 170. KIT Scientific Publishing, 2021, ISSN 2194-1629, doi:10.5445/IR/1000135763, arxiv:2107.11300 (kit.edu).

[25] Karsten Weicker: Evolutionäre Algorithmen. Springer Fachmedien Wiesbaden, Wiesbaden 2015, ISBN 978-3-658-09957-2, doi:10.1007/978-3-658-09958-9 (springer.com [abgerufen am 8. Februar 2022]).

[26] Hartmut Pohlheim: Evolutionäre Algorithmen - Verfahren, Operatoren und Hinweise für die Praxis. VDI-Buch. Springer, Berlin, Heidelberg 2000, ISBN 978-3-642-63052-1, doi:10.1007/978-3-642-57137-4 (springer.com [abgerufen am 8. Februar 2022]).

[27] Ernesto Sanchez, Giovanni Squillero, Alberto Tonda: Industrial Applications of Evolutionary Algorithms. Springer, Berlin, Heidelberg, 2012. doi:10.1007/978-3-642-27467-1

[28] Shu-Heng Chen: Evolutionary Computation in Economics and Finance. Physica, Heidelberg, 2002. S. 6. doi:10.1007/978-3-7908-1784-3

[29] Claus Aranha, Hitoshi Iba: Application of a Memetic Algorithm to the Portfolio Optimization Problem. In: Wayne Wobcke, Mengjie Zhang (Hrsg.): Advances in Artificial Intelligence. AI 2008. LNCS 5360. Springer, Berlin, Heidelberg, 2008. doi:10.1007/978-3-540-89378-3_52

[30] David G. Mayer: Evolutionary Algorithms and Agricultural Systems. Springer, Boston, MA, 2002, S. 2. doi:10.1007/978-1-4615-1717-7

[31] Kalyanmoy Deb: GeneAS: A Robust Optimal Design Technique for Mechanical Component Design. In: Dipankar Dasgupta, Zbigniew Michalewicz (Hrsg.): Evolutionary Algorithms in Engineering Applications. Springer Berlin Heidelberg, Berlin, Heidelberg 1997, ISBN 978-3-642-08282-5, S. 497–514, doi:10.1007/978-3-662-03423-1_27 (springer.com [abgerufen am 8. Februar 2022]).

[32] Thomas Bäck, David Fogel, Zbigniew Michalewicz (Hrsg.): Handbook of Evolutionary Computation. 0. Auflage. Oxford University Press / IOP Publishing, New York 1997, ISBN 978-0-367-80248-6, doi:10.1201/9780367802486 (taylorfrancis.com [abgerufen am 8. Februar 2022]).

[33] Wilfried Jakob, Sylvia Strack, Alexander Quinte, Günther Bengel, Karl-Uwe Stucky: Fast Rescheduling of Multiple Workflows to Constrained Heterogeneous Resources Using Multi-Criteria Memetic Computing. In: Algorithms. Band 6, Nr. 2, 22. April 2013, ISSN 1999-4893, S. 245–277, doi:10.3390/a6020245 (mdpi.com [abgerufen am 8. Februar 2022]).

[34] Alberto Colorni, Marco Dorigo, Vittorio Maniezzo: Genetic Algorithms: A New Approach to the Timetable Problem. In: M. Akgül, H.W. Hamacher, S. Tüfekçi (Hrsg.): Combinatorial Optimization. NATO ASI Series (Series F: Computer and Systems Sciences), Nr. 82. Springer, Berlin, Heidelberg 1992, ISBN 978-3-642-77491-1, S. 235–239, doi:10.1007/978-3-642-77489-8_14 (springer.com [abgerufen am 8. Februar 2022]).

[35] B. Paechter, A. Cumming, H. Luchian: The use of local search suggestion lists for improving the solution of timetable problems with evolutionary algorithms. In: Terence C. Fogarty (Hrsg.): Evolutionary computing: AISB Workshop, Brighton, U.K.: selected papers. Springer, Berlin, Heidelberg 1996, ISBN 3-540-61749-3.

[36] Dipankar Dasgupta: Optimal Scheduling of Thermal Power Generation Using Evolutionary Algorithms. In: Dipankar Dasgupta, Zbigniew Michalewicz (Hrsg.): Evolutionary Algorithms in Engineering Applications. Springer, Berlin, Heidelberg 1997, ISBN 978-3-642-08282-5, S. 317–328, doi:10.1007/978-3-662-03423-1_18 (springer.com [abgerufen am 8. Februar 2022]).

[37] Gary Fogel, David Corne: Evolutionary Computation in Bioinformatics. Morgan Kaufmann, 2002. ISBN 978-1-55860-797-2[https://doi.org/10.1016/B978-1-55860-797-2.X5000-8 10.1016/B978-1-55860-797-2.X5000-8]

[38] Robert Axelrod: Die Evolution der Kooperation. Oldenbourg, München 1987; 7. Auflage, 2014. ISBN 978-3-486-59172-9. doi:10.1524/9783486851748

[39] W. Leo Meerts, Michael Schmitt: Application of genetic algorithms in automated assignments of high-resolution spectra. In: International Reviews in Physical Chemistry. Band 25, Nr. 3, 1. Juli 2006, ISSN 0144-235X, S. 353–406, doi:10.1080/01442350600785490.

[40] A. M. Turing: Computing machinery and intelligence. In: Mind, 59, S. 433–460. 1950. loebner.net (Memento des Originals vom 2. Juli 2008 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2Vorlage:Webachiv/IABot/loebner.net

[:7-41] Ingo Rechenberg: Evolutionsstrategie – Optimierung technischer Systeme nach Prinzipien der biologischen Evolution (PhD thesis) (German). Frommann-Holzboog, 1973. ISBN 3-7728-0373-3

[:8-42] Hans-Paul Schwefel: Evolution and Optimum Seeking. Sixth-generation computer technology series. John Wiley & Sons, New York 1995, ISBN 0-471-57148-2.

[43] John H. Holland: Adaptation in Natural and Artificial Systems. University of Michigan Press, 1975, ISBN 0-262-58111-6.

[:9-44] Darrell Whitley: An overview of evolutionary algorithms: practical issues and common pitfalls. In: Information and Software Technology. Band 43, Nr. 14, Dezember 2001, S. 817–831, doi:10.1016/S0950-5849(01)00188-4 (elsevier.com [abgerufen am 8. Februar 2022]).

[45] Lukáš Sekanina: Evolvable Components: From Theory to Hardware Implementations. Springer, Berlin, Heidelberg, 2004, S. 27. doi:10.1007/978-3-642-18609-7

[46] Cesary Janikow, Zbigniew Michalewicz: An Experimental Comparison of Binary and Floating Point Representations in Genetic Algorithms. In: Conf. Proc of the Fourth Int. Conf. on Genetic Algorithms (ICGA'91). 1991, S. 31–36 (umsl.edu [PDF]).

[47] Zbigniew Michalewicz: Genetic Algorithms + Data Structures = Evolution Programs. Springer, Berlin, Heidelberg 1996, ISBN 978-3-662-03315-9.

[48] Chuan-Kang Ting: On the Mean Convergence Time of Multi-parent Genetic Algorithms Without Selection. In: Advances in Artificial Life, 2005, ISBN 978-3-540-28848-0, S. 403–412.

[49] Ingo Rechenberg: Evolutionsstrategie. Optimierung technischer Systeme nach Prinzipien der biologischen Evolution. Frommann Holzboog, 1973, ISBN 3-7728-0373-3 (Diss. von 1970), Kapitel 15

[50] Julian F. Miller: Cartesian Genetic Programming. Natural Computing Series. Springer, Berlin, Heidelberg, 2011, S. 63. doi:10.1007/978-3-642-17310-3_2