Regler
Der in einem Regelkreis eingebundene Regler wirkt so auf eine Regelstrecke ein, dass eine zu regelnde Größe, die Regelgröße, mit Hilfe einer negativen Rückführung unabhängig von Störeinflüssen sich auf das Niveau der gewählten Führungsgröße einstellt.
Die in unserer Umwelt vorliegenden dynamischen Systeme sind mathematische Modelle zeitabhängiger Prozesse. Sie haben mindestens einen Signaleingang und einen Signalausgang und werden mathematisch über Laplace-transformierte Differenzialgleichungen als Übertragungsfunktionen G(s) definiert. Dies gilt auch für die Regler wie auch Regelstrecken und Regelkreise.
Bekannte Effekte des Regler-Verhaltens sind verstärkende (K), integrierende (I-) und differenzierende (D-) Eigenschaften. Diese Regler in Kombination der dargestellten Varianten des Zeitverhaltens werden als P-, I-, PI-, PD-, PID-Regler bezeichnet. Es existieren aber noch viele andere spezielle Reglerausführungen.
Beispiel eines idealen PID-Reglers in der Summendarstellung der Parameter (Signalflussplan entspricht Paralleldarstellung):
Bei unstetigen Reglern ist die Ausgangsgröße gestuft. Darunter fallen die Zweipunktregler, Mehrpunktregler und Fuzzy-Regler. Optimal angepasste unstetige Regler können ein besseres dynamisches Verhalten der Regelgröße erzielen als die Standardregler.
Siehe auch Hauptartikel Regelungstechnik, Artikel Regelkreis, Artikel Regelstrecke.
Geschichte der Regler
Die Geschichte der Regelungstechnik bzw. die Beschäftigung des Menschen mit der Regelungstechnik begann zwischen dem 3. Jahrhundert v. Chr. und dem 1. Jahrhundert n. Chr. im antiken Griechenland. Das einer Regelung zugrunde liegende Rückkopplungsprinzip ist keine Erfindung des Menschen, sondern ein seit je stattfindendes Naturphänomen. Die moderne Regelungstechnik begann zur Zeit der industriellen Revolution unter Verwendung mechanischer Bauteile. Ihr größter Fortschritt wurde durch die Entwicklung der Elektronik und schließlich durch die elektronische Rechentechnik ermöglicht.
In Bezug zur technischen Gestaltung und der zugehörigen mathematischen Werkzeuge der Regler sind folgende Ereignisse zu nennen:
- 1788 James Watt: Fliehkraftregler (Zentrifugalregulator) zur Drehzahlregelung von Dampfmaschinen.
- 1868 James Clerk Maxwell: Theoretische Analyse des Fliehkraftreglers.
- 1911 Elmer Ambrose Sperry: Reale PID-Regler.
- 1922 Nicolas Minorsky: Herleitung der korrekten mathematischen Formulierung des PID-Reglers.[1]
- 1935 Elektrischer Verstärker.
- 1942 Ziegler / Nichols: Einstellregeln für P-, PI-; PD-, PID-Regler.
- 1945 Bode: Frequenzganganalyse
- 1960 Rudolf Kalman: Kalman-Filter, Zustandsraum, Zustandsregler und Zustandsbeobachter.
- 1965 Lotfi Zadeh: Fuzzy-Set-Theorie als Grundlage für spätere Fuzzy-Regler.
- 1974 Günther Schmidt: Universalregler auf Mikroprozessor-Basis (Digitalregler), mit H. Birk.
Grundlagen der Regler
Einteilung der Regler
Allgemein werden die Regler nach stetigem und unstetigem Verhalten unterschieden. Zu den bekanntesten stetigen Reglern gehören die „Standardregler“ mit P-, PI-, PD- und PID-Verhalten. Ferner gibt es unter den stetigen Reglern verschiedene Sonderformen mit angepasstem Verhalten, um schwierige Regelstrecken regeln zu können. Dazu gehören beispielsweise Regelstrecken mit Totzeiten, mit nichtlinearem Verhalten, mit Drift der Streckenparameter und bekannten und unbekannten Störgrößen.
Bei unstetigen Reglern ist die Ausgangsgröße gestuft. Darunter fallen die Zweipunktregler, Mehrpunktregler und Fuzzy-Regler. Optimal angepasste unstetige Regler können ein besseres dynamisches Verhalten der Regelgröße erzielen als die Standardregler.
Für komplexere Regeleinrichtungen mit nichtlinearen Regelstrecken oder mehrere miteinander verknüpfte Regelgrößen und Stellgrößen sind besonders angepasste Regler – meist digitale Regler – erforderlich. Hierbei kommen vermaschte Regelungen, Mehrgrößenregelungen, Regelungen im Zustandsraum, modellbasierte Regelungen usw. zum Einsatz.
Stetige Regler mit analogem oder digitalem Verhalten können für lineare Regelstrecken verwendet werden. Digitale Regler haben den Vorteil einer universellen Anpassung an die unterschiedlichsten Regelaufgaben, jedoch verlangsamen sie den Regelprozess durch die Abtastzeit der Regelgröße und Rechenzeit im Einsatz bei schnellen Regelstrecken.
Viele nicht stabile Regelstrecken, die zum Beispiel durch positive Rückkopplungseffekte (Mitkopplung) entstehen können, sind ebenfalls mit klassischen linearen Reglern beherrschbar.
Der Entwurf der Regler ist in dem Artikel „Regelkreis“ dargestellt. Siehe auch Artikel „Regelstrecke“ und „Regelungstechnik“.
Beschreibungsfunktionen der Standardregler
Die Übertragungsfunktion ist die häufigste mathematische Beschreibung des Verhaltens linearer Regelkreisglieder und damit die Beschreibung der Regler. Sie entsteht durch die Laplace-Transformation der systembeschreibenden linearen gewöhnlichen Differentialgleichung und ist eine mathematische Beschreibung des Eingangs- und Ausgangsverhaltens eines linearen, zeitinvarianten Übertragungssystems im Frequenzbereich (s-Bereich) mit der komplexen Variable .
Die unabhängige Variable ist ein Symbol für eine vollzogene Laplace-Transformation eines Differentialquotienten. Die Variable – mit einem Exponenten für den Grad der Ableitungen – in verschiedenen Darstellungsarten der Übertragungsfunktion kann beliebig algebraisch behandelt werden, enthält aber keinen Zahlenwert.
Durch die Nullstellenbestimmung lässt sich die Übertragungsfunktion der Polynomdarstellung im Zähler und Nenner in elementare Produkte aufspalten, die als Linearfaktoren bezeichnet werden. Je nach Größe der Zahlenwerte einer Übertragungsfunktion in Polynomdarstellung können die Nullstellen der Polynomzerlegung als Null, als eine reelle Zahl oder als eine konjugiert komplexe Zahl auftreten.
Der Frequenzgang [früher auch ] beschreibt das Verhalten eines linearen zeitinvarianten Übertragungssystems für sinusförmige Ein- und Ausgangssignale.
Die Übertragungsfunktion ist im Gegensatz zum Frequenzgang keine messbare Größe. Die Entstehungsweisen beider Beschreibungsfunktionen und auch deren Anwendung sind unterschiedlich, jedoch kann jederzeit die Übertragungsfunktion bei gleichen Koeffizienten in den Frequenzgang und umgekehrt der Frequenzgang in die Übertragungsfunktion überführt werden, indem der Realteil der komplexen Variablen Null gesetzt wird.
Die Anwendung der Übertragungsfunktion als gebrochen-rationale Funktion ist algebraisch und damit eine große Vereinfachung des mathematischen Aufwandes, lineare Übertragungssysteme zu beurteilen und zu berechnen. So können bei Kenntnis der Übertragungsfunktionen der Regelstrecke durch den Regler Anteile der Strecke mit gleichen Zeitkonstanten kompensiert werden. Dies bedeutet, Linearfaktoren mit Nullstellen des Reglers kompensieren Linearfaktoren mit Polstellen der Strecke um die Ordnung des offenen Regelkreises zu reduzieren. Dies ist sowohl algebraisch als auch durch Betrachtung im Bodediagramm verständlich. Die Auslegung des Regelkreises vereinfacht sich auf diese Weise.
Üblich sind folgende zwei Darstellungsformen der Übertragungsfunktion in der Produktdarstellung:
- Übertragungsfunktion (Linearfaktor) in der Pol-Nullstellen-Darstellung:
- Vorteil: Pole und Nullstellen können für die Frequenzgang-Darstellung direkt abgelesen werden.
- Übertragungsfunktion (Linearfaktor) in der Zeitkonstanten-Darstellung:
- Die Zeitkonstanten errechnen sich aus den Polen und Nullstellen. Die beiden Schreibweisen sind mathematisch identisch.
- Vorteil: Das Zeitverhalten des Systems kann direkt abgelesen werden. Der Verstärkungsfaktor der Übertragungsfunktion bleibt konstant bei Änderung der Zeitkonstante. Die Produktdarstellung mit den Zeitkonstanten hat den höheren Bekanntheitsgrad.
In der linearen Regelungstechnik und Systemtheorie ist es eine willkommene Tatsache, dass praktisch alle vorkommenden regulären (stabilen) Übertragungsfunktionen bzw. Frequenzgänge von Regelkreisgliedern auf drei Grundformen geschrieben bzw. zurückgeführt werden können. Die Linearfaktoren haben eine völlig unterschiedliche Bedeutung, je nachdem ob sie im Zähler oder im Nenner einer Übertragungsfunktion stehen.
Stehen die Linearfaktoren im Zähler, haben sie eine differenzierende Wirkung, stehen sie im Nenner, haben sie eine verzögernde (speichernde) Wirkung:
Typ Linearfaktor Bedeutung im Zähler Bedeutung im Nenner
Nullstelle "Absolutglied fehlt"Differenzierer, D-Glied Integrator, I-Glied
Nullstelle "reelle Zahl"PD1-Glied Verzögerung, PT1-Glied PD2-Glied: für 0 < D < 1
mit konjugiert komplexen NullstellenSchwingungsglied PT2-Glied: für 0 < D < 1
mit konjugiert komplexen Polen- Dabei ist T die Zeitkonstante, s die komplexe Frequenz, D der Dämpfungsgrad.
Übertragungssysteme können definiert werden als:
- Reihenschaltung: .
- Es gilt das Superpositionsprinzip. Die Systeme in Produktdarstellung können in der Reihenfolge beliebig verschoben werden, Systemausgänge werden nicht durch nachfolgende Eingänge belastet.
- Parallelschaltung: ,
- Gegen- und Mitkopplung:
Die linearen Standard-Regler wie:
- P-Regler (P-Glied) mit proportionalem Verhalten,
- I-Regler (I-Glied) mit integralem Verhalten,
- PI-Regler (1 P-Glied, 1 I-Glied) mit proportionalem und integralem Verhalten,
- PD-Regler (PD-Glied) mit proportionalem und differentialem Verhalten,
- PID-Regler (1 I-Glied, 2 PD-Glieder) mit proportionalem, integralem und differentialem Verhalten
lassen sich bereits mit den ersten beiden Grundformen und der Übertragungsfunktionen laut Tabelle in faktorieller Darstellung beschreiben.
Stetige lineare Regler
P-Regler (P-Anteil)
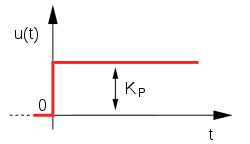
Der P-Regler besteht ausschließlich aus einem proportionalen Anteil der Verstärkung Kp. Mit seinem Ausgangssignal u ist er proportional dem Eingangssignal e.
Das Übergangsverhalten lautet:
- .
Die Übertragungsfunktion lautet:
Das Diagramm zeigt das Ergebnis einer Sprungantwort. Der P-Regler hat eine gewählte Verstärkung von Kp.
Eigenschaften des P-Reglers:
- Reduzierung der Verstärkung: Wegen des fehlenden Zeitverhaltens reagiert der P-Regler unmittelbar, jedoch ist sein Einsatz sehr begrenzt, weil die Verstärkung je nach Verhalten der Regelstrecke stark reduziert werden muss.
- Bleibende Regelabweichung: Der Regelfehler einer Sprungantwort nach dem Einschwingen der Regelgröße als „bleibende Regelabweichung“ beträgt 100 % / Kp, wenn kein I-Glied in der Strecke enthalten ist.
- Regelstrecke als PT1-Glied: Bei einer Regelstrecke mit einem PT1-Glied (Verzögerungsglied 1. Ordnung) kann die Verstärkung theoretisch unendlich hoch gewählt werden, weil ein Regelkreis mit einer solchen Regelstrecke nicht instabil werden kann. Dies kann anhand des Stabilitätskriterium von Nyquist nachgeprüft werden. Die bleibende Regelabweichung ist praktisch vernachlässigbar. Das Einschwingen der Regelgröße ist aperiodisch.
- Regelstrecke als PT2-Glied: Bei einer Regelstrecke mit zwei PT1-Gliedern und zwei dominanten Zeitkonstanten sind die Grenzen dieses Reglers erreicht. Zum Beispiel ergibt für den Fall T1 = T2 beliebiger Größe und einer P-Verstärkung Kp = 10 eine bleibende Regelabweichung von 10 %, eine erste Überschwingung von 35 % bei einem Dämpfungsgrad von ca. D = 0,31. Für T1 ≠ T2 wird die Amplitude der Überschwingung kleiner und die Dämpfung besser. Für ein gleiches Zeitkonstantenverhältnis beliebiger Größe und konstanter P-Verstärkung ergibt sich immer die gleiche Dämpfung.
- Mit steigender P-Verstärkung wird die Regelabweichung kleiner, die Überschwingung größer und die Dämpfung schlechter.
- Integrale Regelstrecke: Die P-Verstärkung kann theoretisch unendlich hoch eingestellt werden, wobei es zu einem aperiodischen Einschwingen der Regelgröße kommt. Bei einer integralen Regelstrecke mit einem PT1-Glied entsteht ein gedämpft schwingender Verlauf der Regelgröße. Instabilität kann nicht entstehen.
I-Regler (I-Anteil)

Ein I-Regler (integrierender Regler, I-Glied) wirkt durch zeitliche Integration der Regelabweichung e(t) auf die Stellgröße mit der Gewichtung durch die Nachstellzeit .
Die Integralgleichung lautet:
Die Übertragungsfunktion lautet:
- Verstärkung
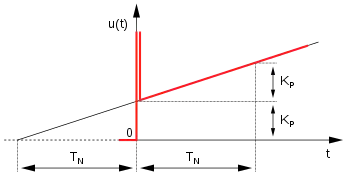
Eine konstante Regeldifferenz e(t) führt von einem Anfangswert des Ausgangs u1(t) zum linearen Anstieg des Ausgangs u2(t) bis zu seiner Begrenzung. Die Nachstellzeit TN bestimmt den Gradienten des Anstiegs.
- für e(t) = konstant
Die Nachstellzeit zum Beispiel TN = 2 s bedeutet, dass zur Zeit t = 0 der Ausgangswert u(t) nach 2 s die Größe des konstanten Eingangswertes e(t) erreicht hat.
Das Diagramm zeigt das Ergebnis der Sprungantwort des I-Gliedes. Die Zeitkonstante beträgt TI = 1 s. Der Eingangssprung hat die Größe
e(t) = 1.
Zusammenfassung der Eigenschaften des I-Reglers:
- Langsamer genauer Regler: Der I-Regler ist durch seine (theoretisch) unendliche Verstärkung ein genauer, aber langsamer Regler. Er hinterlässt keine bleibende Regelabweichung. Weil er eine zusätzliche Polstelle in der Übertragungsfunktion des offenen Regelkreises einfügt und laut Bodediagramm einen Phasenwinkel von −90° verursacht, kann nur eine schwache Verstärkung KI bzw. eine große Zeitkonstante TN eingestellt werden.
- Regelstrecke als PT2-Glied: Für eine Regelstrecke mit zwei PT1-Gliedern kann bei zwei dominanten Zeitkonstanten bereits volle Instabilität bei geringer Verstärkung KI entstehen. Für diese Art Regelstrecken ist der I-Regler kein geeigneter Regler.
- Regelstrecke mit I-Glied: Bei einer Regelstrecke mit I-Glied im Regelkreis ohne zusätzliche Verzögerungen gilt für alle Werte der Kreisverstärkung KI = KI1 * KI2 Instabilität mit konstanter Amplitude. Die Schwingfrequenz ist eine Funktion von KI (für KI > 0).
- Regelstrecke mit dominanter Totzeit: Der I-Regler ist die erste Wahl für eine Regelstrecke mit dominanter Totzeit Tt oder Totzeit ohne weitere PT1-Glieder. Eventuell kann ein PI-Regler eine minimale Verbesserung erzielen. Optimale Einstellung bei vernachlässigbaren Verzögerungsgliedern:
- Die Einstellung KI = 0,5 / Tt führt zu einer Überschwingung von 4 %, die Regelgröße erreicht den Sollwert nach Tt * 3,7 s, Dämpfung D = 0,5. Diese Einstellungen gelten für alle Tt-Werte.
- Wind-up-Effekt bei Großsignalverhalten: Wenn beim I-Regler die Stellgröße u(t) durch die Regelstrecke begrenzt wird, tritt ein Wind-up-Effekt auf. Dabei arbeitet die Integration des Reglers weiter, ohne dass die Stellgröße zunimmt. Wird die Regelabweichung e(t) kleiner, entsteht beim Rücklauf von eine ungewollte Verzögerung der Stellgröße und damit der Regelgröße . Dem tritt man mit der Begrenzung der Integration auf die Stellgrößen-Grenzen entgegen (Anti-wind-up).
- Als eine mögliche Anti-Wind-Up Maßnahme wird der I-Anteil bei Erreichen der Eingangsgrößenbeschränkung auf dem letzten Wert eingefroren (z. B. durch Absperrung des I-Gliedes). Wie bei jedem Begrenzungseffekt innerhalb eines dynamischen Systems verhält sich der Regler nichtlinear. Das Verhalten des Regelkreises ist durch numerische Berechnung zu prüfen. Siehe auch Artikel Regelkreis#Einfluss nichtlinearer Übertragungssysteme auf den Regelkreis mit grafischer Darstellung des Anti-Wind-up Einflusses.
- Grenzzyklen: Bei nichtlinearem Streckenverhalten, insbesondere Haftreibung, kommt es zu sogenannten Grenzzyklen. Hierbei kann das Stellglied den Sollzustand zunächst nicht exakt herstellen, da eine bestimmte minimale Stellgröße nicht zur Überwindung einer Haftreibung ausreicht. Der sich aufbauende I-Anteil sorgt für die Überwindung der Haftreibung, es findet aber unmittelbar der Übergang zur kleineren Gleitreibung statt. Bis sich der I-Anteil auf einen Wert unterhalb der Gleitreibung eingestellt hat, ist der Sollwert überschritten. Der gleiche Vorgang wiederholt sich dann mit umgekehrten Vorzeichen bis zur Ausgangsposition. Es kommt zu einem andauernden Hin-und-her-rucken. Grenzzyklen bzw. Systemunruhe bei konstantem Sollwert können vermieden werden, indem die Stellgröße auf dem bestehenden Niveau gehalten wird, wenn die Regelabweichung innerhalb eines Toleranzbereiches liegt. Wird dies durch eingangsseitige Absperrung des Reglers realisiert (in Software: setzen von e:=0, oder komplettes Aussetzen der Berechnung eines neuen Wertes), statt ausgangseitigem Konstanthalten, wird gleichzeitig ein Kleinsignal-Wind-up-Effekt des Integrators vermieden, der sonst durch die kleinen aber u. U. lange andauernden Abweichungen innerhalb des Toleranzbereichs auftreten kann.
Siehe auch Bode-Diagramm und Ortskurve des Frequenzgangs unter I-Regler.
D-Glied (D-Anteil)
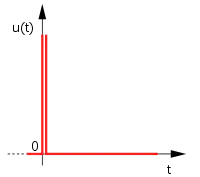
Das D-Glied ist ein Differenzierer, der nur in Verbindung zu Reglern mit P- und/oder I-Verhalten als Regler eingesetzt wird. Er reagiert nicht auf die Höhe der Regelabweichung , sondern nur auf deren Änderungsgeschwindigkeit.
Differentialgleichung:
Übertragungsfunktion:
- mit TV = Vorhaltzeit, TV = KD und KD = Differenzierbeiwert
„Vorhaltzeit“ (Begriff laut DIN 19226 Teil 2) wird umgangssprachlich fälschlicherweise oft als „Vorhaltezeit“ bezeichnet.
Die Sprungantwort des idealen D-Gliedes, wie im zugehörigen Diagramm gezeigt, ist eine Stoßfunktion mit theoretisch unendlicher Größe. Der Eingangssprung ist als Testsignal nicht geeignet.
Ein brauchbares Testsignal für das D-Glied ist die Anstiegsfunktion:
- mit der Anstiegskonstante
Nach der Laplace-Transformation wird
Die Anstiegsfunktion wird in der Übertragungsfunktion des D-Gliedes eingesetzt. Damit wird die Ausgangsgröße des D-Gliedes:
und nach der Rücktransformation wird die Ausgangsgröße:
mit TV = KD
Daraus ist ersichtlich, dass eine Anstiegsfunktion ein konstantes Ausgangssignal am D-Glied hervorruft. Die Größe des Ausgangssignals ist von dem Produkt Anstiegskonstante und Differenzierbeiwert abhängig.
Das bisher betrachtete Verhalten gilt für den idealen Differenzierer. Allgemein gilt ein System, dessen Übertragungsfunktion im Zähler eine höhere Ordnung als im Nenner aufweist, als technisch nicht realisierbar. Es ist nicht möglich, bei einem System mit Nullstellenüberschuss für ein beliebig schnelles Eingangssignal, z. B. für einen Eingangssprung e(t), ein Ausgangssignal u(t) mit unendlich großer Amplitude zu realisieren.
Durch die Umsetzung der Übertragungsfunktion eines idealen Reglers mit D-Anteil in eine Hardware entsteht automatisch eine Verzögerung. Deshalb wird der Übertragungsfunktion des idealen Differenzierers eine kleine Verzögerung (PT1-Glied) zugefügt, deren Zeitkonstante TP – auch parasitäre Zeitkonstante genannt – wesentlich kleiner sein muss als die Zeitkonstante TV.
Die Übertragungsfunktion des realen D-Gliedes lautet damit:
- mit
Eine Sprungantwort des realen D-Gliedes verläuft mit begrenzter Größe des Stoßes asymptotisch nach Null.
Bei der Realisierung des realen D-Gliedes, PD- oder PID-Reglers durch analoge Technik mittels Operationsverstärker ergibt sich unvermeidbar durch Begrenzung der gegengekoppelten Ströme die Verzögerung mit der sogenannten parasitären Zeitkonstante TP, weil der Verstärker innerhalb seines Arbeitsbereichs bleiben muss. (siehe PID-Regler)
Zusammenfassung der Eigenschaften des D-Gliedes:
- Differenzierer: Es kann nur differenzieren, nicht regeln.
- D-Glied als Komponente: Es wird vorzugsweise als Komponente in PD- und PID-Reglern eingesetzt.
- Kompensation I-Glied durch D-Glied: Der Differenzierer kann theoretisch als ideales D-Glied ein I-Glied einer Regelstrecke vollständig bei gleichen Zeitkonstanten kompensieren.
- Anstiegsfunktion als Eingangsgröße: Eine lineare Anstiegsfunktion am Eingang bewirkt eine konstante Ausgangsgröße, die proportional der Zeitkonstante TV ist.
- Sprungantwort des Differenzierers: Die Sprungantwort ist eine Stoßfunktion, die beim realen D-Glied eine endliche Größe aufweist und nach einer e-Funktion auf Null abklingt.
Siehe auch Bode-Diagramm und Ortskurve des Frequenzgangs unter D-Glied!
PI-Regler
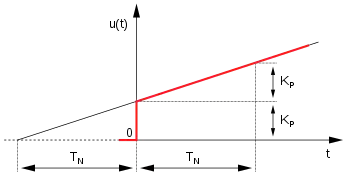
Der PI-Regler (proportional–integral controller) besteht aus den Anteilen des P-Gliedes KP und I-Gliedes mit der Zeitkonstante TN. Er kann sowohl aus einer Parallelstruktur oder aus einer Reihenstruktur definiert werden. Der Begriff der Nachstellzeit TN stammt aus der Parallelstruktur des Reglers.
Integralgleichung des PI-Reglers in der Parallelstruktur:
Übertragungsfunktion der Parallelstruktur:
Wird der Klammerausdruck der Gleichung auf einen gemeinsamen Nenner gebracht, entsteht die Produktdarstellung in der Reihenstruktur:
KPI = KP / TN ist die Verstärkung des PI-Reglers
Aus dieser Produktdarstellung der Übertragungsfunktion ist ersichtlich, dass zwei Regelsysteme als Einzelsysteme zu einer Reihenstruktur geworden sind. Es handelt sich hierbei um ein PD-Glied und um ein I-Glied mit der Verstärkung KPI, welche sich aus den Beiwerten KP und TN errechnen.
Signaltechnisch wirkt der PI-Regler gegenüber dem I-Regler so, dass nach einem Eingangssprung dessen Wirkung um die Nachstellzeit TN vorverlegt ist. Durch den I-Anteil wird die stationäre Genauigkeit gewährleistet, die Regelabweichung wird nach dem Einschwingen der Regelgröße zu Null.
Zusammenfassung der Eigenschaften des PI-Reglers:
- PD-Glied ohne Differenzierung: Das in der Reihenstruktur entstandene PD-Glied des PI-Reglers ist mathematisch ohne Differenzierung entstanden. Deshalb entsteht bei der Realisierung des Reglers in der Parallelstruktur auch keine parasitäre Verzögerung. Wegen eines möglichen Wind-up-Effektes durch Regelstreckenbegrenzung der Stellgröße u(t) ist die schaltungsmäßige Realisierung des PI-Reglers in Parallelstruktur anzustreben.
- Kompensation eines PT1-Gliedes der Strecke: Er kann mit dem PD-Glied ein PT1-Glied der Strecke kompensieren und damit den offenen Regelkreis vereinfachen.
- Keine Regelabweichung bei konstantem Sollwert: Durch das I-Glied wird im stationären Zustand bei konstantem Sollwert die Regelabweichung zu Null.
- Langsamer Regler: Der durch das I-Glied erworbene Vorteil der Vermeidung einer stationären Regelabweichung hat auch den Nachteil, dass eine zusätzliche Polstelle mit −90° Phasenwinkel in den offenen Regelkreis eingefügt wird, was eine Reduzierung der Kreisverstärkung KPI bedeutet. Deshalb ist der PI-Regler kein schneller Regler.
- 2 Einstellparameter: Der Regler enthält nur zwei Einstellparameter, KPI = KP / TN und TN.
- Regelstrecke höherer Ordnung: Er kann optimal an einer Regelstrecke höherer Ordnung eingesetzt werden, von der nur die Sprungantwort bekannt ist. Durch Ermittlung der Ersatztotzeit TU = Verzugszeit und der Ersatzverzögerungs-Zeitkonstante TG = Ausgleichszeit kann das PD-Glied des Reglers die Zeitkonstante TG kompensieren. Für die I-Regler-Einstellung der verbleibenden Regelstrecke mit Ersatztotzeit TU gelten die bekannten Einstellvorschriften.
- Regelstrecke mit 2 dominanten Zeitkonstanten: Er kann eine Regelstrecke mit zwei dominanten Zeitkonstanten von PT1-Gliedern regeln, wenn die Kreisverstärkung reduziert wird und die längere Dauer des Einschwingens der Regelgröße auf den Sollwert akzeptiert wird. Dabei kann mit KPI jeder gewünschte Dämpfungsgrad D eingestellt werden, von aperiodisch (D=1) bis schwach gedämpft schwingend (D gegen 0).
PD-Regler

Der PD-Regler (proportional-derivative controller) besteht aus der Kombination eines P-Gliedes KP mit einem D-Glied. Er kann sowohl als eine Parallelstruktur oder als Reihenstruktur definiert werden.
Die Differentialgleichung der Parallelstruktur lautet:
Die Übertragungsfunktion der Parallelstruktur kann direkt in die Reihenstruktur überführt werden und lautet für den idealen Regler:
Wie beim D-Glied gilt auch hier ein System, dessen Übertragungsfunktion im Zähler eine höhere Ordnung als im Nenner aufweist, als technisch nicht realisierbar. Es ist nicht möglich, bei einem System mit Nullstellenüberschuss für ein beliebig schnelles Eingangssignal, z. B. für einen Eingangssprung e(t), ein Ausgangssignal u(t) mit unendlich großer Amplitude zu realisieren.
Deshalb wird der Übertragungsfunktion des idealen Differenzierers eine kleine ungewollte, aber notwendige „parasitäre“ Verzögerung (PT1-Glied) zugefügt, deren Zeitkonstante TP wesentlich kleiner sein muss als die Zeitkonstante TV.
Die Übertragungsfunktion des realen PD-Reglers lautet damit:
Die Sprungantwort ist wie beim D-Glied eine Stoßfunktion, die beim PD-Regler dem P-Anteil überlagert ist. Deshalb ist die Anstiegsfunktion für den PD-Regler das geeignete Testsignal.
Für die Anstiegsfunktion definiert sich die Vorhaltzeit TV als die Zeit, bei der ein reiner P-Regler vor Beginn der Anstiegsfunktion beginnen müsste, um auf den Wert zu kommen, den das D-Glied bewirkt.
Der PD-Regler ist ein sehr schneller Regler, denn er fügt im Gegensatz zum PI-Regler keinen zusätzlichen Pol durch Integration in den offenen Regelkreis ein. Selbstverständlich ist auch die unvermeidbare parasitäre Verzögerung mit kleiner Zeitkonstante im Regelkreis nicht vernachlässigbar.
Zusammenfassung der Eigenschaften des PD-Reglers:
- Kompensation eines PT1-Gliedes: Er kann ein PT1-Glied der Regelstrecke kompensieren und damit die Regelstrecke vereinfachen.
- Regelstrecke mit 2 PT1-Gliedern: Der ideale PD-Regler kann gegenüber dem P-Regler bei einer Regelstrecke mit zwei PT1-Gliedern theoretisch mit unendlich hoher Verstärkung arbeiten. Die bleibende Regelabweichung ist in diesem Fall praktisch vernachlässigbar. Das Einschwingen der Regelgröße ist aperiodisch.
- Bleibende Regelabweichung: Der Regelfehler einer Sprungantwort nach dem Einschwingen der Regelgröße als bleibende Regelabweichung beträgt 100*KP/ (KP+1) [%].
PD2-Glied mit konjugiert komplexen Nullstellen
PD2-Glieder mit konjugiert komplexen Nullstellen können Schwingungsglieder (PT2-Glieder) mit konjugiert komplexen Polen vollständig kompensieren, wenn die Größe der Zeitkonstanten beider Systeme identisch ist.
PD2kk-Glieder mit konjugiert komplexen Nullstellen erhält man, indem von der Übertragungsfunktion eines PD2-Gliedes in Polynom-Darstellung der mittlere Term der Übertragungsfunktion durch ein bestimmtes D-Glied subtrahiert wird. Mit dieser Maßnahme entsteht ein System mit kunjugiert komplexen Nullstellen.
Die Übertragungsfunktion eines PD2-Gliedes mit gleichen Zeitkonstanten lautet:
Die Übertragungsfunktion eines D-Gliedes lautet:
PD2-Glied mit konjugiert komplexen Nullstellen durch Subtraktion mit D-Glied:
Diese Übertragungsfunktion kann per Hardware oder Software realisiert werden.
Wenn Zahlenwerte der PD2kk-Übertragungsfunktion vorliegen, gilt die Normalform mit den Beiwerten a und b:
Daraus ergeben sich die Parameter einer PD2-Übertragungsfunktion mit konjugiert komplexen Nullstellen:
Bezeichnet man bei diesem Zählerpolynom analog zum Nennerpolynom (PT2KK-Schwingungsglied) mit D den Dämpfungsgrad:
Bei D ≥ 1 ergeben sich reale Nullstellen anstelle der konjugiert komplexen Nullstellen.
PID-Regler
Der PID-Regler (proportional-integral-derivative controller) besteht aus den Anteilen des P-Gliedes, des I-Gliedes und des D-Gliedes. Er kann sowohl aus der Parallelstruktur oder der Reihenstruktur definiert werden.
In dem Blockdiagramm sind die Reihenstruktur (Produktdarstellung) und die Parallelstruktur (Summendarstellung) der Übertragungsfunktionen des realen PID-Reglers dargestellt. Die Begriffe idealer und realer PID-Regler kennzeichnen, ob die durch den D-Anteil notwendige unvermeidliche Verzögerung (PT1-Glied) berücksichtigt ist.
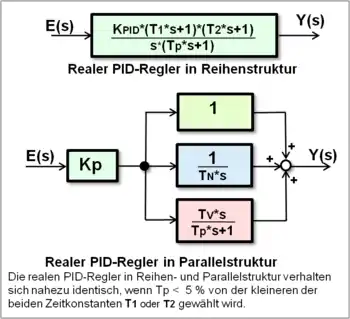

Die Begriffe der P-Verstärkung KP, Vorhaltzeit TV und der Nachstellzeit TN entstammen der parallelen Reglerstruktur. Sie haben einen hohen Bekanntheitsgrad in der Anwendung empirischer Regler-Einstellungen bei Regelkreisen mit unbekannten Regelstrecken und geringen dynamischen Anforderungen.
Beide Darstellungsformen der parallel- und reihenstrukturierten PID-Regler, die sich mathematisch völlig identisch umrechnen lassen, haben unterschiedliche Vorteile in der Anwendung:
- Die Reihenstruktur des PID-Reglers und die zugehörige Übertragungsfunktion erlauben für den Reglerentwurf die einfache Pol-Nullstellen-Kompensation von Regler und Regelstrecke. Ferner ist diese Darstellungsform für Anwendungen im Bodediagramm geeignet.
- Die Parallelstruktur des PID-Reglers ermöglicht das Verhindern des Wind-up-Effekts. Sehr häufig wird die Stellgröße des Reglers u(t) in Regelkreisen durch die Regelstrecke begrenzt. Dadurch entsteht das ungewollte Verhalten des I-Gliedes, bis zu seiner eigenen Begrenzung weiter zu integrieren. Verschwindet die Stellgrößenbegrenzung, weil die Regelabweichung gegen Null läuft, hat das I-Glied einen zu hohen Wert und verursacht eine schlechte Einschwingdynamik der Regelgröße y(t). Siehe Anti-Wind-up-Maßnahme im Kapitel I-Regler dieses Artikels und Artikel Regelkreis, Kapitel: Einfluss nichtlinearer Übertragungssysteme auf den Regelkreis.
Differenzialgleichung des idealen PID-Reglers in Parallelstruktur:
Übertragungsfunktion des idealen PID-Reglers in Parallelstruktur (Summendarstellung):
Wird der Klammerausdruck der Gleichung auf einen gemeinsamen Nenner gebracht, entsteht die Polynomdarstellung der Parallelstruktur des PID-Reglers.
Übertragungsfunktion des idealen PID-Reglers der Parallelstruktur in Polynomdarstellung:
Das Zählerpolynom kann durch die Bestimmung der Nullstellen aufgelöst werden. Damit lautet die Übertragungsfunktion des idealen PID-Reglers in Reihenstruktur als Produktdarstellung:
mit der Reglerverstärkung
Wie beim D-Glied und PD-Regler gilt auch hier ein System, dessen Übertragungsfunktion im Zähler eine höhere Ordnung als im Nenner aufweist, als technisch nicht realisierbar. Es ist nicht möglich, bei einem System mit Nullstellenüberschuss für ein beliebig schnelles Eingangssignal, z. B. für einen Eingangssprung e(t), ein Ausgangssignal u(t) mit unendlich großer Amplitude zu realisieren.
Wird ein PID-Regler durch Beschaltung eines Operationsverstärkers realisiert, so muss für den D-Anteil und die damit verwendete Kapazität ein Widerstand den Strom im Summenpunkt begrenzen, damit der Verstärker innerhalb seines Arbeitsbereichs bleibt. Damit entsteht ungewollt aber unvermeidbar eine zusätzliche Verzögerung als PT1-Glied, dessen Zeitkonstante gegenüber der Zeitkonstante TV wesentlich kleiner sein muss. Dieses Verzögerungsglied wird auch als parasitäre Verzögerung mit der Zeitkonstante TP bezeichnet.
Die Parameter des idealen und des realen PID-Reglers können zwischen den parallelen und reihenförmigen Strukturen beliebig umgerechnet werden. Die Umrechnung des realen PID-Reglers bezieht sich auf die gleiche Zeitkonstante TP in beiden Reglerstrukturen. Die Umrechnungsgleichungen entstehen durch Ausmultiplizieren beider Übertragungsfunktionen und Vergleich der Koeffizienten an den Laplace-Operatoren s und s².
Empfehlung des PID-Reglerentwurfs mit Reduzierung des Wind-up-Effekts:
- Auslegung des realen PID-Reglers nach der Reihenstruktur zur Kompensation der PT1-Glieder der Regelstrecke. Die parasitäre Zeitkonstante soll so klein wie möglich sein, z. B. 5 % von T1;2 der kleineren der beiden Zeitkonstanten.
- Umrechnung des realen PID-Reglers der Reihenstruktur in die Parallelstruktur und nachfolgende Hardware-Realisierung des Reglers. Wird die gleiche parasitäre Zeitkonstante der Reihenstruktur verwendet, haben beide Reglerstrukturen identische Eigenschaften.
Die mathematische Beschreibung der beiden Strukturen des idealen und realen Reglers ist in der nachfolgenden Tabelle dargestellt.
PID-Regler Übertragungsfunktion, Parameter Bemerkung Idealer PID-Regler
ReihenstrukturEmpfohlener Reglerentwurf:
Pol-Nullstellen-KompensationIdealer PID-Regler
Parallelstruktur
PID-Parallelstruktur,
gemeinsamer Nenner.
Polynom für Faktorisierung.Idealer PID-Regler
Umrechnung Reihenstruktur
in ParallelstrukturReglerparameter aus Zeit-
konstanten berechnen.Idealer PID-Regler
Umrechnung Parallelstruktur
in ReihenstrukturModifizierte pq-Formel zur Berechnung der Zeitkonstanten
wenn
, dann Polynom
konjugiert komplexRealer PID-Regler
Reihenstruktur mit
parasitärer ZeitkonstanteParasitäre Zeitkonstante:
der kleineren Zeitkonst.Realer PID-Regler
Parallelstruktur mit
parasitärer ZeitkonstanteParasitäre Zeitkonstante:
der kleineren Zeitkonst.Realer PID-Regler
Umrechnung Reihenstruktur
in Parallelstruktur
Umrechnung gilt für die
gleiche Zeitkonstante Tp in
Reihen und Parallelstruktur
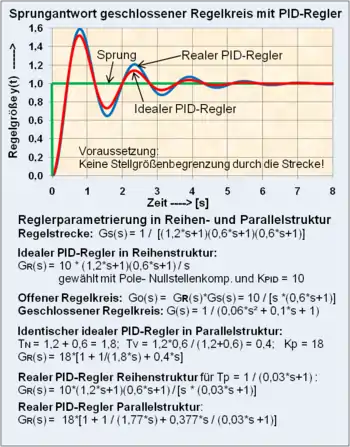
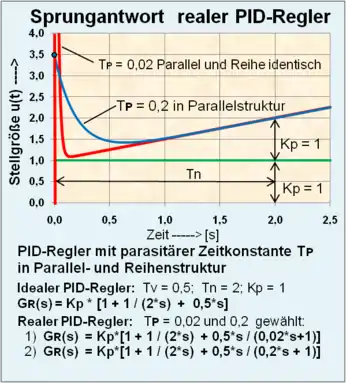
Das grafische Beispiel der Sprungantwort eines Regelkreises mit PID-Regler-Parametrierung und Pol-Nullstellen-Kompensation zeigt (in der Bildvergrößerung) die unterschiedlichen Übertragungsfunktionen der Regler in der Reihen- und Parallelstruktur mit identischen Eigenschaften. Das parasitäre Zeitglied des realen Reglers, zum Unterschied zum idealen PID-Regler, verursacht im Regelkreis größere Überschwingungen und damit eine schlechtere Dämpfung der Regelgröße y(t).
Zusammenfassung der Eigenschaften des PID-Reglers:
- Anpassungsfähigkeit an eine Regelstrecke: Er ist von den Standard-Reglern am anpassungsfähigsten, verhindert bei konstantem Sollwert eine bleibende Regelabweichung bei Führungs- und Störgrößensprung und kann 2 Verzögerungen (PT1-Glieder) der Regelstrecke kompensieren und damit die Regelstrecke vereinfachen.
- Langsamer Regler: Der durch das I-Glied erworbene Vorteil der Vermeidung einer stationären Regelabweichung bei konstantem Sollwert hat auch den Nachteil, dass eine zusätzliche Polstelle mit −90° Phasenwinkel in den offenen Regelkreis eingefügt wird, was eine Reduzierung der Kreisverstärkung KPID bedeutet. Deshalb ist der PID-Regler (wie auch der PI- und I-Regler) kein schneller Regler.
- Einstellparameter: Er enthält 3 Einstellparameter, KPID, T1, T2 des idealen PID-Reglers in Reihenstruktur, bzw. KP, TN, TV des idealen Reglers in Parallelstruktur. Die bei der Realisierung des realen Reglers verwendete parasitäre Zeitkonstante TP ergibt sich aus der verwendeten Hardware. TP sollte möglichst sehr klein sein gegenüber TV.
- Regelstrecke mit 3 PT1-Gliedern: Er kann eine Regelstrecke mit 3 dominanten Zeitkonstanten von PT1-Gliedern regeln, wenn die Kreisverstärkung reduziert wird und die längere Dauer des Einschwingens der Regelgröße auf den Sollwert akzeptiert wird. Dabei kann mit KPID jeder gewünschte Dämpfungsgrad D eingestellt werden, von aperiodisch (D=1) bis schwach gedämpft schwingend (D gegen 0).
- Integrale Regelstrecke mit PT1-Glied: Er kann eine Regelstrecke mit I-Glied und einem PT1-Glied optimal regeln.
- Regelstrecke mit dominanter Totzeit: Der PID-Regler ist an einer Regelstrecke mit dominanter Totzeit ungeeignet.
Zustandsregler
Der Zustandsregler ist kein eigenständiger Regler, sondern er entspricht der mit Faktoren bewerteten Rückführung der Zustandsgrößen eines mathematischen Modells der Regelstrecke im Zustandsraum.
Das Grundprinzip des Zustandsreglers (auch statische Zustandsrückführung genannt) ist die Rückführung der bewerteten inneren Systemgrößen eines Übertragungssystems zu einem Regelkreis. Die einzelnen Zustandsgrößen werden mit Faktoren bewertet und wirken subtraktiv auf die Führungsgröße w(t).
Damit durchlaufen Anteile der Zustandsgrößen ein zweites Mal die Integrationskette der Rechenschaltung laut Signalflussplan der Regelungsnormalform. Das Ergebnis ist ein Zustandsregler mit PD-Verhalten im Zustandsregelkreis.
Im Gegensatz zu einem Standardregelkreis wird die Ausgangsgröße y(t) des Zustandsregelkreises nicht auf den Eingang der Regelstrecke zurückgeführt. Der Grund liegt darin, dass die Ausgangsgröße y(t) eine Funktion der Zustandsgrößen ist. Dennoch kann ein nicht akzeptabler proportionaler Fehler zwischen den Werten der Führungsgröße w(t) und der Regelgröße y(t) entstehen, der durch ein Vorfilter V beseitigt werden muss.
Eine Alternative zur Vermeidung einer Regelabweichung bietet ein überlagerter Regelkreis des Zustandsregelkreises mit einem PI-Regler mit Rückführung der Regelgröße y(t), der das Vorfilter V überflüssig macht.
Siehe detaillierte Begriffsklärung unter Regelstrecke im Zustandsraum.
Regler mit Zustandsrückführung
Indizierung:
- Matrizen = Großbuchstaben mit Unterstrich,
- Vektoren = Kleinbuchstaben mit Unterstrich,
- Transponierte Vektordarstellung, Beispiel:
- Standardmäßig liegt ein Vektor immer in Spaltenform vor. Um einen Zeilenvektor zu erhalten, muss ein Spaltenvektor transponiert werden.
Die Regler-Zustandsrückführung (zur Unterscheidung der Rückführung der Zustandsgrößen) bezieht sich auf den Zustandsvektor , der mittels Vektorverstärkung laut dem Signalflussplan des Modells des Zustandsregelkreises auf die Eingangsgröße zurückgeführt wird:
Der lineare Zustandsregler bewertet die einzelnen Zustandsvariablen der Regelstrecke mit Faktoren und summiert die so entstandenen Zustandsprodukte zu einem Soll-Istwert-Vergleich.[2]
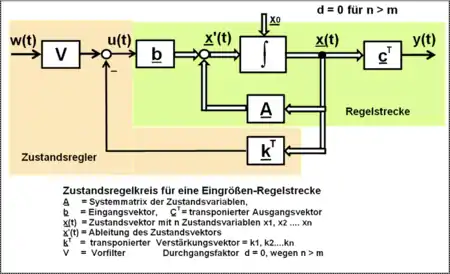
Die mit dem Regler zurückgeführten bewerteten Zustandsgrößen durchlaufen noch einmal das Zustandsraum-Modell der Strecke und bilden neue Kreis-Zustandsgrößen, wodurch differenzierendes Verhalten entsteht. Deshalb entspricht die Wirkung der zurückgeführten Zustandsgrößen je nach Höhe der Ordnung n der Differenzialgleichung der Strecke der eines -Reglers.[3]
Die nachfolgenden einfachen algebraischen Gleichungen beziehen sich auf die Zustandsdifferentialgleichung der Größe laut des um die Regler-Zustandsrückführung erweiterten Blockschaltbildes des Zustandsraum-Modells für eine Eingrößen-Regelstrecke.
Gleichung der Zustandsregler-Rückführung :
Die Standardform der Zustandsdifferenzialgleichung (vereinfacht auch Zustandsgleichung genannt) der Regelstrecke lautet:
Wird die Gleichung der Reglerrückführung für in die Zustandsgleichung eingesetzt, dann ergibt sich die Gleichung des Zustandsdifferenzialgleichung des Regelkreises.
Für regelungstechnische Belange hat die Regelstrecke von Ausnahmen abgesehen immer mehr Pole als Nullstellen. Für n > m vereinfacht sich die Ausgangsgleichung, weil der Durchgriff (bzw. ) gleich Null wird. Ist die Regelstrecke ein lineares System, so ergeben sich folgende Zustandsgleichungen des Regelkreises:
- Gleichungen des Regelkreis-Zustandsraummodells laut des dargestellten grafischen Signalflussplanes:
Gleichung Bei Eingrößensystemen Zustandsdifferenzialgleichung
des RegelkreisesAusgangsgleichung
des Regelkreises
d = 0 für n > m
Gleichung Bei Mehrgrößensystemen Zustandsdifferenzialgleichung
des RegelkreisesAusgangsgleichung
des Regelkreises
= 0 für n > m
Für Zustandsregler gibt es im Wesentlichen zwei Entwurfsverfahren. Beim Reglerentwurf zur Polzuweisung (engl. pole placement) werden für Ein- oder Mehrgrößensysteme gewünschte Eigenwerte des Regelkreises durch die Regler-Rückführung festgelegt. Die Güteforderungen aus dem Zeitbereich werden in die Lage der Eigenwerte übersetzt. Die Pole können genau dann beliebig vorgegeben werden, wenn die zu regelnde Strecke vollständig steuerbar ist. Andernfalls gibt es einzelne feste Eigenwerte, die nicht verändert werden können.
Auch der Entwurf eines LQ-Reglers, ein Verfahren zur optimalen Regelung, basiert auf der Struktur der Zustandsrückführung. Jedes Entwurfsverfahren muss auf eine stabile Matrix (oder ) führen, damit der Regelkreis stabil ist.
Die Zustandsrückführung erfordert die Kenntnis des Zustandes zu jedem Zeitpunkt. Ist die Regelstrecke beobachtbar, so kann der Zustandsvektor durch Einsatz eines Beobachters aus den Ausgangsgrößen rekonstruiert werden.
Siehe Grafikdiagramme für ein Berechnungsbeispiel eines Zustandsreglers im Artikel Zustandsraumdarstellung.
Regler mit Ausgangsrückführung
Begriffsklärung:
- Zustandsrückführung
- In einem Regelkreis werden über einen Verstärkungsvektor die so bewerteten Zustandsgrößen (= Zustandsvektor ) der Regelstrecke zurückgeführt zu einem Soll-Istwert-Vergleich mit der Führungsgröße w(t).
- Ausgangsrückführung
- In einem Regelkreis mit einer im Zustandsraum definierten Regelstrecke wird die Regelgröße y(t) zu einem Soll-Istwert-Vergleich zurückgeführt. Die Zustandsgrößen werden nicht genutzt.
- Ein Regelkreis mit Zustandsrückführung kann durch einen überlagerten I- oder PI-Regelkreis mit einer Ausgangsrückführung ausgestattet werden. Damit wird das Vorfilter V überflüssig und die Regelabweichung theoretisch zu Null.
Fazit:
Bei Verzicht auf den Aufwand der Erfassung der Zustandsgrößen steht für den Entwurf eines Reglers nur die Ausgangsrückführung der Regelstrecke zur Verfügung. Bei einer Regelstrecke als Eingrößensystem bedeutet die Ausgangsrückführung für einen Regelkreis, dass es sich um einen Standardregelkreis handelt.
Ein Regler mit einer Ausgangsrückführung kann einen optimierten Regler mit einer Zustandsrückführung nicht ersetzen, weil die Zustandsgrößen dynamisch schneller als die Ausgangsrückführungen reagieren.
Bei Mehrgrößen-Regelstrecken mit Ausgangsrückführungen handelt es sich um Mehrgrößenregelungen. Die Beschreibung derartiger Mehrgrößensysteme erfolgt ebenfalls in der Matrizen / Vektor-Darstellung.
Regler für Mehrgrößensysteme
Wie auch der Zustandsregler ist der Mehrgrößenregler kein eigenständiger Regler, sondern er ist auf eine Mehrgrößen-Regelstrecke angepasst.
Bei vielen technischen Prozessen müssen mehrere physikalische Größen gleichzeitig geregelt werden, wobei diese Größen voneinander abhängig sind. Bei Änderung einer Eingangsgröße (Stellgröße u(t)) wird zusätzlich eine andere Ausgangsgröße (Regelgröße y(t)) oder auch alle anderen Ausgangsgrößen beeinflusst.
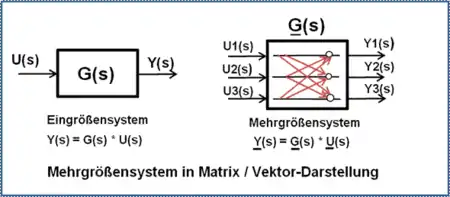
Bei Mehrgrößen-Regelstrecken sind die Eingangsgrößen und Ausgangsgrößen untereinander verkoppelt. Im Regelkreis sind die r Eingangsgrößen der Regelstrecke U1(s) bis Ur(s) die Stellgrößen des Systems, die entsprechend dem Kopplungsgrad mehr oder weniger auf die verschiedene Anzahl m der Regelgrößen Y1(s) bis Ym(s) einwirken können.
Beispiele von einfachen Mehrgrößensystemen:
- Bei der Dampferzeugung sind Druck und Temperatur gekoppelt,
- Bei Klimaanlagen sind Temperatur und Luftfeuchtigkeit gekoppelt.
Für den einfachen Fall der Verkopplung einer Regelstrecke mit 2 Eingängen und 2 Ausgängen treten die häufigsten symmetrischen Verkopplungsarten in P- und V-kanonischer Struktur auf. Bei der P-kanonischen Struktur wirkt ein Eingang der Strecke über ein Koppelelement auf den nicht zugehörigen Ausgang der Strecke. Bei der V-kanonischen Struktur wirkt ein Ausgang der Strecke über ein Koppelelement auf den nicht zugehörigen Eingang der Strecke.
Je nach Art der gekoppelten Regelstrecken können für den Reglerentwurf 3 Konzepte gewählt werden:
- Dezentrale Regelung
- Jedem Stell- und Regelgrößenpaar wird ein eigener Regler zugeordnet. Die auf diesen Regelkreis durch die Kopplung einwirkenden Störungen werden durch den Regler kompensiert. Dieses Verfahren ist bei schwacher Kopplung oder bei langsamen Koppelsystemen gegenüber der Hauptregelstrecke akzeptabel.
- Regelung mit Entkopplung
- Jedem Stell- und Regelgrößenpaar wird ein Hauptregler und für die Kopplungen zwischen den Stell- und Regelgrößen je ein Entkopplungsregler zugeordnet. Es ist Aufgabe der Entkopplungsregler, den Einfluss der anderen Stellgrößen auf die jeweilige Regelgröße zu eliminieren oder zumindest zu reduzieren.
- Echte Mehrgrößenregelung
- Der Mehrgrößenregler hat so viele Eingänge wie Regelgrößen und so viele Ausgänge wie Stellgrößen. Die Kopplungen zwischen den Komponenten werden in einem einheitlichen Reglerkonzept berücksichtigt. Der Entwurf der Mehrgrößenregler erfolgt über die Matrizen-Vektorrechnung.
Dezentrale Regler bei Mehrgrößen-Regelstrecken
Bei Mehrgrößensystemen sind die Eingangsgrößen U(s) mit den Ausgangsgrößen Y(s) untereinander über gekoppelte Übertragungssysteme schwach bis stark gekoppelt.
Bei Regelstrecken mit identischer Anzahl von Ein- und Ausgängen mit schwacher Kopplung werden dezentrale Regler für jede Hauptstrecke eingesetzt und die Kopplung bleibt unberücksichtigt. Die eingekoppelten Signalgrößen werden als Störgrößen betrachtet.
Für den dezentralen Regler gilt der konventionelle Entwurf des Reglers mit der Beschreibung der Übertragungsfunktion aller Komponenten unter Vernachlässigung der gegenseitigen Beeinflussung durch Koppelelemente.
Bei einem Einsatz von Standardreglern bietet sich als einfachste Entwurfsstrategie die Pole-Nullstellenkompensation des Reglers mit der Hauptregelstrecke des offenen Regelkreises an. Mit der inversen Laplace-Transformation des geschlossenen Regelkreises kann für ein Eingangs-Testsignal die P-Verstärkung des Regelkreises optimiert werden. Die Ausgangsgröße y(t) kann grafisch dargestellt werden.
Es ist zu beachten, dass die Stellgrößen der Regler nicht durch die Regelstrecken begrenzt werden, anderenfalls sind diese Berechnung und auch alle anderen Methoden der Reglerdimensionierung im komplexen Frequenzbereich nicht gültig.
Sind nichtlineare Elemente oder eine Systemtotzeit in der Strecke enthalten, kann ein optimaler Regler durch numerische Berechnung bestimmt werden. Entweder werden kommerzielle Rechenprogramme verwendet oder alle nichtlinearen Komponenten werden durch logische Gleichungen, alle linearen Komponenten durch Differenzengleichungen für diskrete Zeitintervalle Δt beschrieben.
Mehrgrößenregler mit Entkopplung
Regelstrecken mit starker Kopplung erfordern Mehrgrößenregler, anderenfalls kann die gegenseitige Beeinflussung der Signalgrößen zu einem unbefriedigenden Regelverhalten des Gesamtsystems bis zum Verlust der Stabilität führen.
Für den einfachen Fall der Verkopplung einer Regelstrecke mit 2 Eingängen und 2 Ausgängen treten die häufigsten symmetrischen Verkopplungsarten in P- und V-kanonischer Struktur auf.[4][5]
Bei der P-kanonischen Struktur wirkt ein Eingang der Strecke über ein Koppelelement (Koppelglied) auf den nicht zugehörigen Ausgang der Strecke. Bei der V-kanonischen Struktur wirkt ein Ausgang der Strecke über ein Koppelelement auf den nicht zugehörigen Eingang der Strecke. Die Koppelelemente können statisches, dynamisches oder beide Eigenschaften aufweisen.
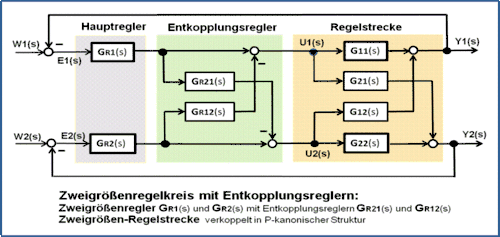
Moderne regelungstechnische Methoden basieren fast alle auf der P-kanonischen Struktur. Liegt das Modell in der Regelstrecke als V-kanonische Struktur vor, kann es in die P-kanonische Struktur umgerechnet werden. Die Regelstrecken und die Entkopplungsregeler können auch in beliebiger Struktur-Mischform realisiert werden.
Die beste Strategie der Entkopplung ist das Einfügen von Entkopplungsreglern, deren Wirkung auf die Entkopplung der Regelstrecke beschränkt ist. Damit kann man die 2 entkoppelten Regelkreise als unabhängige Eingrößenregelkreise betrachten und nachträgliche Parameteränderungen der Regler durchführen. Die ursprüngliche verkoppelte Regelstrecke mit den Hauptregelstrecken G11(s) und G22(s) ändert sich wie nachfolgend dargestellt auf 2 unabhängige Regelstrecken GS1(s) und GS2(s):
Der Entkopplungsregler wird zuerst entworfen. Er ist nur abhängig von den Regelstrecken und deren Verkopplung. Die Übertragungsfunktion der Entkopplungsregler für GR12(s) und GR21(s) lautet:
Entkopplungsregler GR12(s) und GR21(s)
Ersatzregelstrecke GS1(s)
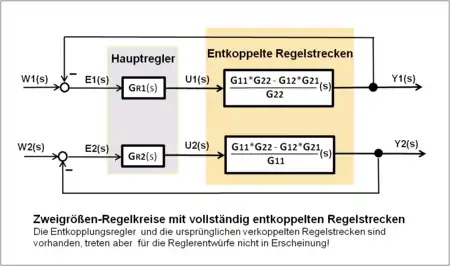
Die zwei offenen unabhängigen entkoppelten Regelkreise haben sich bezüglich der Regelstrecke durch die Kopplungselemente geändert. Die neue Regelstrecke GS1(s) besteht aus der Parallelschaltung der Zweige: G11(s) parallel zu (−1) * GR21(s) * G12(s)
Die Übertragungsfunktion der neuen Regelstrecke GS1(s) lautet:
Wird in diese Gleichung die Gleichung für GR21(s) eingesetzt, dann erhält man die neue Übertragungsfunktion der Strecke GS1(s), die in Verbindung mit dem zugehörigen Entkopplungsregler völlig unabhängig ist. Sie ist nur abhängig von den Übertragungsgliedern der ursprünglichen Strecke mit ihren Verkopplungen:
Ersatzregelstrecke GS2(s)
Die zwei offenen unabhängigen entkoppelten Regelkreise haben sich bezüglich der Regelstrecke durch die Kopplungselemente geändert. Die neue Regelstrecke GS2(s) besteht aus der Parallelschaltung der Zweige: G22(s) parallel zu (−1) * GR12(s) * G21(s)
Die Übertragungsfunktion der neuen Regelstrecke GS2(s) lautet:
Wird in diese Gleichung die Gleichung für GR12(s) eingesetzt, dann erhält man die neue Übertragungsfunktion der Strecke GS2(s), die in Verbindung mit dem zugehörigen Entkopplungsregler völlig unabhängig ist. Sie ist nur abhängig von den Übertragungsgliedern der ursprünglichen Strecke mit ihren Verkopplungen:
Der Regelentwurf kann wie in dem Kapitel – „Dezentrale Regler bei Mehrgrößen-Regelstrecken“ geschildert – erfolgen.
Mehrgrößenregler beliebiger Strukturen
Der „echte“ Mehrgrößenregeler hat so viele Eingänge r wie Regelgrößen (wie auch Regelabweichungen) und so viele Ausgänge m wie Stellgrößen.
Die übliche Systembeschreibung von Mehrgrößensystemen erfolgt durch die Übertragungsfunktion aller Elemente in der Matrizen / Vektor-Darstellung. Wie bei Eingrößensystemen ist auch bei Mehrgrößensystemen die charakteristische Gleichung des geschlossenen Regelkreises mit ihren Eigenwerten für die Stabilität verantwortlich.[6]
Bei einschleifigen Regelkreisen wird der Nenner der Übertragungsfunktion des Regelkreises gleich Null gesetzt.
Der Regelkreis ist stabil, wenn die Wurzeln der charakteristischen Gleichung sich in der linken s-Halbebene befinden. (Siehe Bedeutung der Pole und Nullstellen der Übertragungsfunktion)
Nachfolgend werden die Schritte beschrieben, um die Übertragungsfunktionsmatrix des geschlossenen Regelkreises und die zugehörige charakteristische Gleichung zu ermitteln:
- Aufstellung der Übertragungsmatrix der verkoppelten Regelstrecke,
- Aufstellung des Matrix-Vektor-Produktes des offenen Regelkreises,
- Aufstellung der Übertragungsfunktionsmatrix des geschlossenen Mehrgrößenregelkreises,
- Darstellung der charakteristischen Gleichung in Matrix-Vektor-Darstellung und skalarer Darstellung.
Um die mathematische Beschreibung einfach zu gestalten, wird von Systemen mit 2 gekoppelten Ein- und Ausgangsgrößen ausgegangen. Eine Erweiterung auf Systeme mit mehreren Ein- und Ausgangsgrößen ist möglich.
Aufstellung der Übertragungsmatrix der verkoppelten Regelstrecke
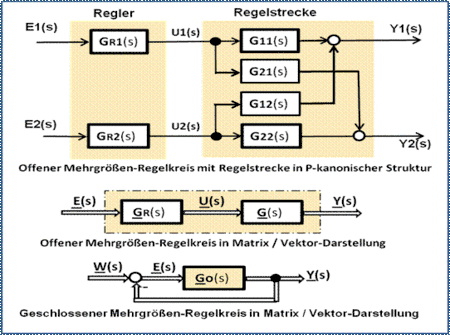
Laut des dargestellten Blockdiagramms eines offenen Regelkreises wirkt in einem Zweigrößensystems ein Regler GR(s) auf eine Regelstrecke G(s). Die Kopplung der Regelstrecke ist in P-kanonischer Struktur ausgeführt.
Aus dem Blockschaltbild des offenen Regelkreises können die skalaren Gleichungen der Regelstrecke direkt abgelesen werden:
Aufstellung des Matrix-Vektor-Produktes des offenen Regelkreises
In Matrix-Schreibweise ergibt sich folgende Darstellung als Übertragungsmatrix:
Allgemein lässt sich eine Regelstrecke mit r Eingängen (Stellgrößen) und m Ausgängen (Regelgrößen) durch folgende Matrixgleichung beschreiben:
Die genannten Größen haben folgende Bedeutung:
- = Strecken-Übertragungsmatrix,
- = Regelgrößenvektor,
- = Stellgrößenvektor.
Fasst man die Strecken-Übertragungsmatrix und die Regler-Übertragungsmatrix zusammen, dann ergibt sich folgende Matrixgleichung des offenen Regelkreises:
Aufstellung der Übertragungsfunktionsmatrix des geschlossenen Mehrgrößenregelkreises
Die Übertragungsfunktionsmatrix des offenen Regelkreises kann mit der Schließbedingung zu einem geschlossenen Regelkreis überführt werden.
Danach lautet die Matrixgleichung der Regelgröße laut des Blockdiagramms:
Die Schließbedingung mit der Matrix für den r-fachen Regelkreis ergibt:
Damit lautet die Übertragungsfunktionsmatrix des geschlossenen Regelkreises:
Darstellung der charakteristischen Gleichung in Matrix-Vektor-Darstellung und skalarer Darstellung
Der Eigenvorgang des geschlossenen Regelkreises wird beschrieben durch:
In Matrizendarstellung lautet diese Gleichung:
Eine Lösung dieses Gleichungssystems existiert nur dann, wenn die Determinante von () verschwindet. Man erhält die charakteristische Gleichung des Mehrfachregelkreises:
Damit ist gezeigt, dass ein Mehrgrößensystem wie ein Eingrößensystem auch nur eine charakteristische Gleichung besitzt, die das Stabilitätsverhalten bestimmt.
Der geschlossene Mehrgrößenregelkreis ist dann E/A-stabil, wenn alle Pole (beziehungsweise je nach Betrachtung die Wurzeln) der charakteristischen Gleichung einen negativen Realteil haben.
Nichtlineare Regler
Bei linearen zeitinvarianten Systemen (LZI-System) ohne Energiespeicher ist die Ausgangsgröße proportional der Eingangsgröße. Bei linearen Systemen mit Energiespeichern ist die Ausgangsgröße im eingeschwungenen Zustand der Eingangsgröße proportional. Bei Systemen mit integralem Verhalten (I-Glied) ist die Ausgangsgröße proportional des zeitlichen Integrals der Eingangsgröße. Bei Systemen mit differenzierendem Verhalten (D-Glied) ist die Ausgangsgröße proportional des Differentialquotienten der Eingangsgröße.
Mathematische Operationen von Signalen bezogen auf die Ausgangsgröße wie:
- Additionen, Subtraktionen, Differentiationen, Integrationen oder Multiplikationen mit einem konstanten Faktor von Eingangssignalen ergeben lineares Verhalten.
- Multiplikation und Division von Eingangsgrößen ergeben nichtlineares Verhalten.
Bei nichtlinearen Übertragungssystemen wirkt mindestens eine nichtlineare Funktion in Verbindung mit linearen Systemen. Diese nichtlinearen Funktionen werden nach stetigen und unstetigen Nichtlinearitäten unterschieden. Stetige Nichtlinearitäten weisen keine Sprünge der Übertragungskennlinie auf wie z. B. bei quadratischem Verhalten. Unstetige Übertragungskennlinien wie bei Begrenzungen, Hysterese, Ansprechempfindlichkeit, Zwei- und Mehrpunkt-Charakter haben keinen kontinuierlichen Verlauf.
Das Prinzip der Superposition gilt nicht bei nichtlinearen Übertragungssystemen.
Zu den nichtlinearen Reglern gehören auch die unstetigen Regler wie Zweipunkt-, Mehrpunkt- und Fuzzy-Regler, die in einem eigenen Kapitel beschrieben sind.
Die Berechnung von nichtlinearen Systemen geschieht meist im Zeitbereich. Die Lösung von nichtlinearen Differentialgleichungen ist schwierig und aufwendig. Dies bezieht sich besonders auf die Gruppe der Systeme mit unstetigem nichtlinearem Übertragungsverhalten bzw. nichtstetigen Reglern. Einfacher ist die Berechnung eines Regelkreises mit schaltenden Reglern mit rechnergestützten zeitdiskreten Verfahren.
Fuzzy-Regler (Übersichtsdarstellung)
- Siehe Hauptartikel: Fuzzy-Regler
Fuzzy-Regler arbeiten mit sogenannten „linguistischen Variablen“, welche sich auf „unscharfe Mengenangaben“ beziehen, wie zum Beispiel hoch, mittel und niedrig. Die „Regelbasis“ verknüpft die fuzzifizierten Ein- und Ausgangssignale mit logischen Regeln wie WENN-Teil und DANN-Teil. Mit der Defuzzifizierung wird die unscharfe Menge wieder in scharfe Stellbefehle gewandelt (z. B. Ventilkombinationen für „Kraft Aufbau“ oder „Kraft Abbau“ oder „Kraft halten“).
Ein grafisches Fuzzy-Modell zeigt eine Fuzzy-Variable als skalierte Grundmenge (z. B. Temperaturbereich), deren meist dreieckförmige Teilmengen (Fuzzy-Sets) auf der Abszisse eines Koordinatensystems meist überlappend aufgeteilt sind. Die Ordinate zeigt den Zugehörigkeitsgrad für jeden scharfen Wert der Eingangsgröße an. Der maximale Wert des Zugehörigkeitsgrades für jeden Fuzzy-Set beträgt μ = 1 ≡ 100 %.
Anwendung Fuzzy-Controller
Die Hauptanwendung der Fuzzy-Logik bezieht sich auf Fuzzy-Controller für Prozesse mit mehreren Ein- und Ausgangsgrößen, deren mathematische Modelle aufwändig oder schwierig zu beschreiben sind. Dies sind meist technische Prozesse mit konventionellen Verfahren, die korrigierende Eingriffe von Menschenhand (Anlagenfahrer) erfordern, oder wenn der Prozess nur manuell gefahren werden kann. Das Ziel der Anwendung der Fuzzy-Logik ist, solche Prozesse zu automatisieren.
Anwendungsbeispiele sind die Steuerung von Schienenfahrzeugen oder Regalförderanlagen, bei denen Fahrzeiten, Bremswege und Positionsgenauigkeiten von den Massen, Förderwegen, Schienenhaftwerten und Zeitplänen abhängig sind. Im Allgemeinen handelt es sich bei diesen Prozessen um Mehrgrößensysteme, deren Führungsgrößen Programm-gesteuert und -geregelt werden. Einfachere Anwendungen im privaten Haushalt finden sind als Wasch- und Geschirrspülmaschinen.
Die Grundidee des Fuzzy-Controllers bezieht sich auf die Anwendung des Expertenwissens mit linguistischen Begriffen, durch die der Fuzzy-Controller optimiert wird, ohne dass ein mathematisches Modell des Prozesses vorliegt. Der Fuzzy-Controller hat keine dynamischen Eigenschaften.
Diese Anwendungen der Fuzzy-Controller als Kennfeld-Controller in Mehrgrößensystemen gelten als robust und arbeiten auch bei Änderung der Prozess-Parameter noch relativ zuverlässig.
Fuzzy-Regler in Eingrößensystemen
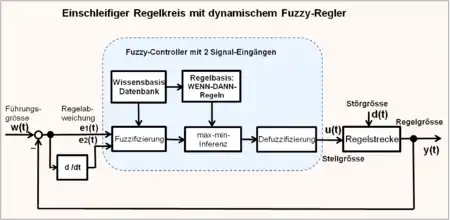
Die auf die Fuzzy-Logik basierenden Fuzzy-Regler sind statische nichtlineare Regler, deren Eingangs-Ausgangkennlinie in Abhängigkeit von den gewählten Fuzzy-Sets und deren Bewertung (Regelbasis) abhängt. Die Eingangs-Ausgangskennlinie kann in allen Quadranten des Koordinatensystems, speziell nichtlinear durch den Ursprung im 1. und 3. Quadranten, lückend (Ausgangsgröße = 0) in der Nähe des Ursprungs oder nur positiv im 1. Quadranten verlaufen. Sie kann als extremes Beispiel durch Wahl der Lage der Fuzzy-Sets auch linear verlaufen oder ein klassisches 3-Punkt-Regelverhalten zeigen.
Fuzzy-Regler haben keine dynamischen Komponenten. Als Eingrößensysteme sind sie deshalb im Verhalten mit einem Proportional-Regler (P-Regler) vergleichbar, dem in Abhängigkeit von den linguistischen Variablen und deren Bewertung eine beliebige nichtlineare Kennlinie gegeben wird. Deshalb sind Fuzzy-Regler für lineare Eingrößen-Regelstrecken einem optimierten konventionellen Standardregler mit PI-, PD- oder PID-Verhalten hoffnungslos unterlegen.
Fuzzy-Regler können durch Erweiterung der Eingangskanäle mit integralem und differenziellem Anteil zu einem PID-Verhalten modifiziert werden. Sie haben gegenüber dem klassischen PID-Regler keinen funktionellen Vorteil, sind aber fähig, eine nichtlineare Funktion der Regelstrecke zu kompensieren. Bei zwei oder mehreren Signal-Eingängen wird der Fuzzy-Regler zu einem Kennfeldregler.
Adaptive Regler
- Hauptartikel: Adaptive Regelung
Adaptive Regler sind Regler, die ihre Parameter automatisch an die Regelstrecke anpassen. Sie sind somit zur Regelung zeitvarianter Regelstrecken geeignet.
Extremwertregler
- Hauptartikel: Extremwertregelung
Extremwertregler dienen dazu, den Prozess in einen aus Sicht des Anwenders optimalen Zustand zu führen und dort zu halten. Sie werden dort verwendet, wo sich aus den Messgrößen gegenüber den Stellgrößen ein Kennfeld ergibt, das ein Extremum aufweist.
Unstetige Regler
Bei unstetigen Reglern (auch nichtstetige Regler) ist die Ausgangsgröße u(t) gestuft. Bei einem einfachen Zweipunktregler kann die Ausgangsgröße des Reglers – die Stellgröße u(t) – nur 2 diskrete Zustände annehmen: Ist die Regelabweichung e(t) = w(t) – y(t) positiv, schaltet der Zweipunktregler ein, ist sie Null oder negativ schaltet der Regler aus. Hat der Regler eine symmetrische Hysterese, muss die Regelabweichung stets einen kleinen Betrag negativ werden, damit der Regler ausschaltet und einen gleichen kleinen Betrag positiv werden, damit der Regler einschaltet.
Unstetige Regler mit den Ausgangssignalzuständen „Ein“ oder „Aus“ können auch ein proportionales Verhalten haben, wenn die Ausgangsgröße eines klassischen Standardreglers mit einem Pulsbreiten-Modulator versehen wird. Die Regelstrecke wirkt dabei zur Glättung der gepulsten Signale als Tiefpass. Zweck dieses Verfahrens ist die möglichst verlustfreie Steuerung großer Energieflüsse.
Bei der Verwendung elektrischer und elektronischer Schaltelemente wie Relais, Schaltschütze, Transistoren und Thyristoren ist eine möglichst niedrige Schaltfrequenz anzustreben, um Bauelemente-Verschleiß und Alterung gering zu halten. Auch elektronische Bauelemente unterliegen einer Alterung, wenn sie bei erhöhter innerer Temperatur betrieben werden. Andererseits bedeutet eine niedrige Schaltfrequenz eine Erhöhung der Welligkeit des Signals der Regelgröße.
Wegen der durch steile Impulsflanken verursachten elektromagnetischen Störungen der Schaltvorgänge sind geeignete Entstörmaßnahmen vorzusehen. (Siehe Elektromagnetische Verträglichkeit)
Wie auch bei linearen Übertragungssystemen interessiert die Stabilität eines Regelkreises mit nichtstetigen Reglern.
Die effektivste Berechnungsmethode für den Entwurf, die Analyse und der Optimierung eines nichtstetigen Reglers im Regelkreis-Modell ist numerisch durch kommerzielle Rechenprogramme wie mit MATLAB oder Simulink zu erreichen.
Liegen solche Rechenprogramme nicht vor, so können mit der Kombination logischer Gleichungen und Differenzengleichungen beliebige Systeme und Regelkreise mit stetigen, unstetigen, nichtlinearen und linearen Elementen relativ einfach mit beliebigen Rechenprogrammen – vorzugsweise Tabellenkalkulation – numerisch für eine diskrete Zeit Δt berechnet werden. Das Verhalten der relevanten Regelkreissignale für ein Test-Eingangssignal kann direkt tabellarisch und grafisch dargestellt werden. (Siehe Artikel Regelkreis#Numerische Berechnung dynamischer Übertragungssysteme (Übersichtsdarstellung) und Regelkreis#Regelkreis mit unstetigen Reglern)
Zweipunktregler
Zweipunktregler können nicht nur einfachste Regelaufgaben zufriedenstellend lösen. Sie vergleichen die Regelgröße mit einem meist hysteresebehafteten Schaltkriterium und kennen nur zwei Zustände: „Ein“ oder „Aus“. Diese so definierten Zweipunktregler haben theoretisch kein Zeitverhalten.
Darunter fallen die elektromechanischen Regler oder Schaltkomponenten wie z. B. Bimetall-Schalter, Kontaktthermometer, Lichtschranken. Häufig sind diese einfachen Regler nur für einen festen Sollwert geeignet.
Das Hystereseverhalten des realen elektromechanischen Zweipunktreglers entsteht meist durch Reibungseffekte, mechanisches Spiel, zeitabhängige elastische Materialverformungen und Mitkopplung des Systemausgangs auf den Eingang.
Elektronische Zweipunktregler erlauben eine sehr gute Anpassung an die Regelstrecke. Dafür werden 2 wichtige Eigenschaften des Reglers erforderlich. Die sich automatisch einstellende Schaltfrequenz des Regelkreises muss durch einzustellende Parameter erhöht oder reduziert werden, um eine gewünschte optimale Schaltfrequenz zu erzielen.
Dazu wird der ideale elektronische Zweipunktregler durch folgende Schaltungsmaßnahmen erweitert:
- definierte (harte) Hysterese durch Mitkopplung des Reglerausgangs zum Eingang (additiver Einfluss),
- Zeitverhalten durch verzögernde oder verzögernd nachgebende Rückführung auf das Eingangssignal (subtraktiver Einfluss).
Damit kann hinsichtlich der unterschiedlichen Arten der Regelstrecken ein gewünschtes Verhalten der Regelgröße und der Schaltfrequenz erreicht werden.
Für spezielle Anwendungen der Regler und Stellglieder kann die Signalverarbeitung auch auf der Basis von pneumatischen oder hydraulischen Medien erfolgen. Die Gründe dafür sind: explosive Materialien in der Umgebung, hohe elektromagnetische Störstrahlung, keine elektrische Energie vorhanden, pneumatische oder hydraulische Energieeinrichtungen sind bereits vorhanden.
Richtig angepasste Zweipunktregler an eine Regelstrecke können für die Regelgröße y(t) bessere dynamische Eigenschaften als die Anwendung eines stetigen Standardreglers bieten.
Anwendungen des Zweipunktreglers
- Regelstrecken mit Beharrungsverhalten
- Grundsätzlich können nur Regelstrecken ohne I-Verhalten eingesetzt werden, deren Ausgangsgröße im stationären Zustand einem Beharrungszustand anstrebt. Wenn der Zweipunktregler einen positiven und negativen Ausgang (alternativ einen aktiven 2. Ausgang) hat, können theoretisch auch I-Regelstrecken und instabile PT1-Glieder geregelt werden. In der Praxis kommen für motorische Stellantriebe Dreipunktregler zum Einsatz, die eine Kennlinie mit einer „Totzone“ aufweisen und damit einen schaltfreien Ruhezustand ermöglichen.
- Stellglieder des Reglers
- Die Schnittstelle „Ausgang des Reglers“ und „Eingang der Regelstrecke“ ist meist durch eine gegebene Regelstrecke festgelegt. Für die Anwendung des Zweipunktreglers kommen nur Regelstrecken-Eingänge mit Zweipunktverhalten in Frage. Das sind zum Beispiel Schütze, Ventile, Magnete und andere elektrische Anlagen.
- Kleine elektrische Leistungen können mit Relais, Bimetall-Schaltern und Transistoren gesteuert werden. Für die Steuerung großer elektrischer Leistung des Stellgliedes werden Schütze, Leistungstransistoren und Thyristoren eingesetzt.
- Genauigkeitanforderungen
- Einfache Regelkreise mit geringen Genauigkeitsanforderungen, bei denen eine bestimmte Welligkeit (Oszillation) um den Wert der Regelgröße akzeptiert wird, können mit elektromechanischen Reglern betrieben werden. Dies gilt insbesondere für Regelstrecken mit großen Zeitkonstanten.
- Bei großen Genauigkeitsanforderungen an die Regelgröße sind angepasste elektronische Zweipunktregler erforderlich. Dies gilt für schnelle Regelstrecken, gewünschtem quasistetigen Verhalten der Regelgröße und gute Störunterdrückung.
Zweipunktregler mit Hysterese
Für die Berechnung bzw. die Simulation eines Schaltregelkreises muss das Verhalten des Zweipunktreglers klar definiert sein. Der ideale Zweipunktregler vergleicht ein Eingangssignal e(t) > 0 und e(t) < 0 und liefert ein Ausgangssignal u(t) = UMAX oder u(t) = u(0). Bei einer Regelstrecke 1. Ordnung würde durch den idealen Zweipunktregler eine sehr hohe Schaltfrequenz entstehen, die durch die zufällig gewählten Schaltkomponenten und der Regelstrecke bestimmt wäre. Deshalb erhält ein komfortabler realer Schaltregler eine möglichst einstellbare Hysterese zugeordnet.
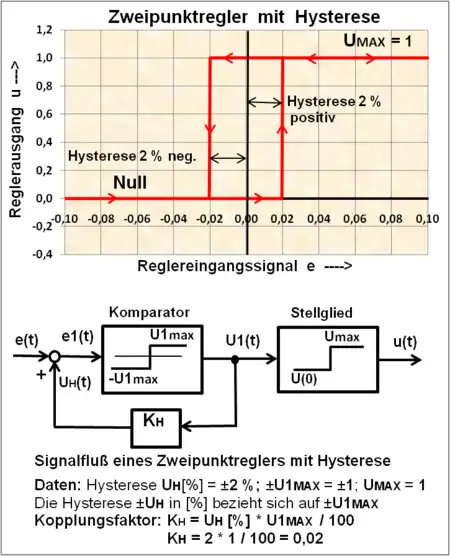
Wichtigste Komponente dieses idealen Zweipunktreglers ist der Komparator, der 2 Spannungen vergleicht. Durch positive Rückführung (Mitkopplung) eines einstellbaren kleinen Anteil der Ausgangsgröße wird das Hystereseverhalten erreicht. Eine symmetrische Hysterese für das Eingangssignal e(t) > Null und e(t) < Null entsteht, wenn die Ausgangsgröße des Komparators positive und negative Werte annehmen kann. Eine Endstufe sorgt dann für die Beziehungen:
Die Größe der Hysterese bezieht sich laut Signalflussplan auf das Ausgangssignal des idealen Zweipunktreglers u1(t) = ±U1MAX, das über den Kopplungsfaktor KH auf den Eingang des Reglers positiv zurückgeführt wird. Diesen Anteil muss die Regelabweichung e(t) als Eingangsgröße des Reglers überschreiten oder unterschreiten, damit der Zweipunktregler reagiert.
Der symmetrische Bereich der Hysterese beträgt:
Der Kopplungsfaktor KH kann empirisch bei der Auslegung des Reglers festgelegt werden. Der symmetrische Hystereseeinfluss UH kann auch in [%] des Reglerausgangs u1(t) = U1MAX definiert werden:
Der Kopplungsfaktor KH beträgt für UH[%]:
Schaltfrequenz im Regelkreis
Die Schaltfrequenz eines Regelkreises mit einem realen Zweipunktregler wird bestimmt durch:
- die Größe der Zeitkonstanten der Regelstrecke,
- die Ordnung der Differenzialgleichung bzw. der Übertragungsfunktion der Regelstrecke,
- die Größe der Hysterese des Reglers,
- eine evtl. vorhandene Totzeit der Regelstrecke,
- eine positive Rückführung über ein zeitverzögerndes Element am Regler-Ausgang,
- in geringem Maße durch die Größe des Sollwertes.
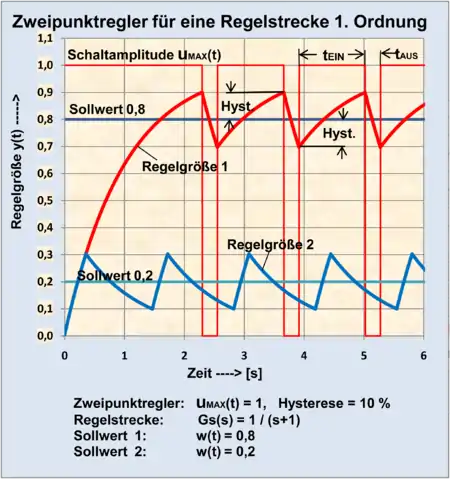
Die Schaltfrequenz fSCHALT ergibt sich durch die Größe der Einschaltzeit tEIN und der Ausschaltzeit tAUS im Regelkreis und bestimmt damit die Periodendauer.
Die optimale Schaltfrequenz ist erreicht, wenn eine weitere Zunahme der Frequenz nur höhere Schaltverluste bringt, ohne die Regelabweichung der Regelgröße zu verbessern, beziehungsweise wenn die Schaltüberlagerungen der Regelgröße unterhalb der angezielten Genauigkeitsklasse liegen.
Der Einfluss der Hysterese wirkt als Verzögerung der zeitabhängigen Regelabweichung e(t). Die Regelabweichung muss im positiven und im negativen Bereich die Größe der Hysterese überwinden, bis der Regler reagiert. Die Größe der Hysterese verstimmt die Regelabweichung und damit die Regelgröße. In vielen Fällen reicht eine Hysterese von 0,1 % bis 1 % der Stellgröße.
Im Regelkreis mit einem realen Zweipunktregler mit Hysterese wird mit steigender Hysterese die Schaltfrequenz niedriger. Bei einer Regelstrecke 1. Ordnung ergibt sich eine sehr hohe Schaltfrequenz, die durch die Einstellung einer größeren Hysterese reduziert wird.
Für eine PT1-Regelstrecke mit einem Zweipunktregler mit Hysterese kann der Verlauf der Regelgröße y(t) als Sprungantwort grafisch konstruiert werden. Es handelt sich dabei um Ausschnitte des exponentiellen Anstiegs und Abfalls des Verlaufs des geschalteten PT1-Gliedes entsprechend der Zeitkonstanten.
Eine Regelstrecke höherer Ordnung kann als ein System mit Ersatztotzeit aufgefasst werden und führt zu einer niedrigen Schaltfrequenz. Durch zusätzliche Rückführungsmaßnahmen der Stellgröße u(t) kann die Schaltfrequenz erhöht und eine zufriedenstellende Regeleigenschaft erreicht werden.
Eine echte Systemtotzeit in der Größe von mehr als 10 % der dominanten Zeitkonstante der Regelstrecke führt zu einer niedrigen Schaltfrequenz und damit zu großer Welligkeit des Signals der Regelgröße mit annäherungsweise 10 %. Zusätzliche Rückführungsmaßnahmen der Stellgröße ergeben nur mit einer verzögert nachgebenden Rückführung eine Verbesserung. Je größer die dominante Zeitkonstante der Regelstrecke ist, umso weniger kritisch ist die Einstellung der Reglerparameter. Der Schaltregler ist je nach Anspruch an die Genauigkeit der Regelgröße für Regelstrecken mit Totzeit in dynamischer Hinsicht besser geeignet als ein stetiger Standardregler.
Mathematische Behandlung des Zweipunktreglers im Regelkreis
Für die Berechnung des Regelkreises werden häufig normierte Größen eingeführt. Handelt es sich zum Beispiel um eine Temperaturregelung, bei der die elektrische Energie über ein Schütz oder über eine Leistungselektronik zugeführt wird, können der Sollwert w(t), die Stellgröße u(t) und die Regelgröße y(t) in der Dimension Temperatur ausgedrückt werden. Die Sprungantwort der Stellgröße u(t) für den Wert UMAX stellt sich erst nach einer theoretisch unendlich langen Zeit an der Regelstrecke ein.
Für die Normierung der Systemgrößen können die maximalen Werte der Führungsgröße w(t) und der Regelgröße y(t) des Regelkreises mit 100 % oder mit 1 dargestellt werden. Die maximale Stellgröße UMAX muss größer als die maximale Regelgröße sein.
Die Stellgröße u1(t) = ±U1MAX kann in einem beliebigen Verhältnis zu ±UMAX stehen und wird meist durch die verwendeten Elektronik-Bausteine bestimmt. Die Größe der Hysterese UH ist abhängig von ±U1MAX und dem Kopplungsfaktor UK.
Es ist zu beachten, dass die Aufheizzeitkonstanten der Regelstrecke nicht identisch mit den Abkühlzeitkonstanten sein müssen.
Die einzig sinnvolle und relativ einfache Berechnungsmethode eines Regelkreises mit Zweipunkt und Mehrpunkt-Reglern ist die Anwendung kommerzieller Rechenprogramme oder die numerische Behandlung mit der diskretisierten Zeit Δt auf der Basis logischer Gleichungen kombiniert mit den Differenzengleichungen linearer Systeme. Das zeitliche Verhalten sämtlicher Regelkreisgrößen wird tabellarisch und grafisch direkt dargestellt.
Die numerische Beschreibung des Zweipunktreglers mit Hysterese besteht aus einer einfachen linearen und 2 nichtlinearen Gleichungen. Die logische Beschreibung kann mit der WENN-, DANN-; SONST-Anweisung der Tabellenkalkulation laut des dargestellten Signalflussplanes erfolgen.
Dieser Regler hat kein Zeitverhalten, aber er bewirkt an seinem Ausgang eine Phasenverschiebung zu einem zeitabhängigen Eingangssignal.
Die 3 folgenden numerisch zu lösenden Gleichungen sind in der Reihenfolge festgelegt und werden durch Rekursion gelöst.
Lineare numerische Gleichung der Rückführung für das Hystereseverhalten:
(Anmerkung: ist laut der Gleichungsreihenfolge noch nicht bekannt)
Nichtlineare Gleichung des Komparators:
Nichtlineare Gleichung der Stellgröße:
Die Indizierungen mit n bedeuten: n = (0; 1; 2; 3; …) = Rekursionsfolge, n-1 = um eine Folge zurückliegendes Ergebnis.
Für die Berechnung eines Regelkreises werden für eine Rekursionsfolge der gleichen Zahl n alle Systeme der Systemkette hintereinander mit der diskreten Zeit Δt berechnet. n * Δt ist die aktuelle Zeit der Folge n.
Die Rekursionsfolge für eine beliebige Zahl von n lautet für einen Regelkreis:
- Regelabweichung E(n) = W(n) - Y(n-1),
- Regler: Gleichungen des Zweipunktreglers,
- Regelstrecke mit linearen Elementen: Differenzengleichungen
Im Artikel Regelkreis mit dem Kapitel Unstetige Regler wird der Entwurf mit unstetigen Reglern behandelt.
Zweipunktregler mit zeitabhängiger Rückführung
Einfachste Bimetall-Regler, die bei Heizanlagen meist nur auf einen festen Temperatur-Schaltpunkt reagieren, sind seit langem im Einsatz. Um Überschwingungen der Regelgröße bei einem Sollwertsprung zu vermeiden und um die Schaltfrequenz zu erhöhen, wird durch den aktiven Einschaltvorgang des Schaltreglers gleichzeitig durch eine kleine Heizquelle der Bimetall-Regler zum vorzeitigen Abschalten geführt. Dieses Verhalten bezeichnet man mit „Thermischer Rückführung“.
Elektronische Regler mit einer zeitabhängigen Rückführung des Ausgangssignals erlauben eine beliebige Anpassung des Reglers an die Regelstrecke. Sie wirken alle subtrahierend auf die Regelabweichung und erhöhen damit die Schaltfrequenz. Nachteilig wirkt bei größerem Einfluss die damit verbundene Verstimmung der Regelabweichung und damit die Abweichung der Regelgröße vom Sollwert.
Eine wesentlich bessere Eigenschaft der Rückführung ergibt sich, wenn die Verstimmung der Regelabweichung nur vorübergehend wirkt und dann exponentiell abnimmt.
Durch folgende bekannte Rückführungsmaßnahmen des Zweipunktregler wird die Dynamik des Regelkreises verbessert:
- Zweipunktregler mit nachgebender Rückführung
- Die Stellgröße des Reglers wirkt auf ein PT1-Glied, dessen Ausgangssignal subtraktiv die Regelabweichung beeinflusst. Ein Faktor KR beispielsweise im Bereich 10 % Umax bestimmt den Einfluss der Rückführung. Da die Rückführung entsprechend der sich einstellenden Schaltfrequenz ständig das Signal der Regelabweichung in Form einer sägezahnförmigen Spannung mit Gleichspannungsanteil verstimmt, ist diese Art für genaue Regelungen nicht zu empfehlen.
- Mit steigender Zeitkonstante der Rückführung wird die Schaltfrequenz des Regelkreises niedriger. Mit steigender Verstärkung mit dem Faktor KR wird die Schaltfrequenz höher, die Regelabweichung größer und das Überschwingverhalten der Regelgröße geringer.
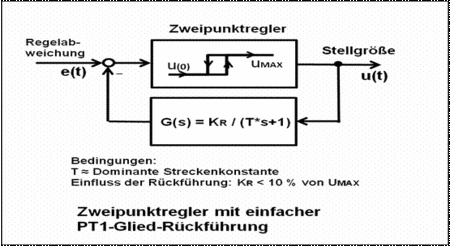
- Zweipunktregler mit nachgebender Rückführung entsprechen annähernd dem Verhalten eines PD-Reglers. Überschwingungen nach einem Sollwertsprung werden reduziert. Eine ständige Regelabweichung im stationären Zustand steht an.
- Übertragungsfunktion der Rückführung mit einem PT1-Glied lautet:
- Die mathematische Beschreibung des Zweipunktreglers mit Hysterese und der nachgebenden Rückführung besteht aus 2 einfachen linearen und 2 nichtlinearen Gleichungen. Die logische Beschreibung kann mit der WENN-, DANN-; SONST-Anweisung der Tabellenkalkulation laut des dargestellten Signalflussplanes erfolgen.
- Es gilt noch die numerische Gleichung der Rückführung für den Hysterese-Effekt:
- Das Hysterese-Produkt wird zu addiert, die nachgebende Rückführung uR(t) von subtrahiert.
- Die zugehörige numerische Gleichung lautet:
- Logische Gleichung des Zweipunktreglers:
- Logische Gleichung der Stellgröße:
- Differenzengleichung des PT1-Gliedes der Rückführung:
- Zweipunktregler mit verzögert-nachgebender Rückführung
- Variante: 2 parallelgeschaltete PT1-Glieder in Differenzschaltung[7]
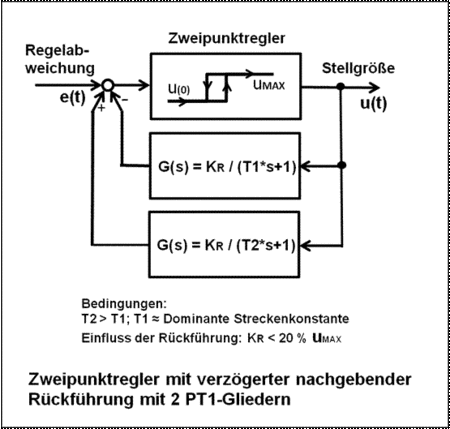
- Erweitert man die nachgebende Rückführung um einen Parallelzweig mit einem weiteren PT1-Glied mit größerer Zeitkonstante, das additiv die Regelabweichung beeinflusst, dann verläuft die Sprungantwort dieser Rückführung nach genügend langer Zeit zu dem Wert Null.
- Im stationären Zustand einer beliebigen Schaltfrequenz im Regelkreis subtrahieren sich die Gleichspannungsanteile der beiden zurückgeführten sägezahnförmigen Signale der PT1-Glieder. Aktiv bleibt die relativ kleine Differenz der beiden Welligkeiten als Wechselspannungsüberlagerung um die Regelabweichung des Niveaus Null. Die Amplituden dieser Welligkeit sind durch die Größe der Hysterese beziehungsweise durch die sich einstellende Schaltfrequenz gegeben.
- Das Ergebnis der Sprungantwort (Übergangsfunktion) dieser Rückführung in Differenzschaltung ist ein einzelner exponentiell schnell ansteigender und dann exponentiell flach gegen Null abfallender sinusähnlicher Impuls. Aufgabe des Impulses ist die Verstimmung der Regelabweichung und damit die vorzeitige Abschaltung der Stellgröße, bevor die Regelgröße den Sollwert erreicht.
- Als Regler-Entwurfsstrategie ist die Dauer des Impulses der maximalen Anstiegszeit der Regelgröße bis zum Erreichen des Sollwertes anzupassen. Bei geeigneter Auslegung der Rückführung und der Hysterese des Reglers kommt es im Regelkreis bei einem größeren Sollwertsprung zu einer vorzeitigen Abschaltung des Stellgliedes und Reduzierung der Überschwingung der Regelgröße. Die Regelabweichung ist im stationären Zustand nahezu Null.
- Übertragungsfunktion der Rückführung:
- für T2R > T1R
- Die Interpretation des PID-ähnlichen Verhaltens ist bei Zweipunktreglern so zu verstehen, dass der D-Anteil des Reglers dem vorzeitigen Abschalten des Reglerausgangs entspricht und das I-Verhalten des Reglers durch die hohe Schaltverstärkung erreicht wird, durch die kaum eine relevante Regelabweichung entsteht. Vorausgesetzt ist, dass der Regelkreis auf die optimale Schaltfrequenz eingestellt ist.
- Zweipunktregler mit verzögert-nachgebender Rückführung
- Variante: 2 PT1-Glieder mit einem D-Glied in Produktform[8]
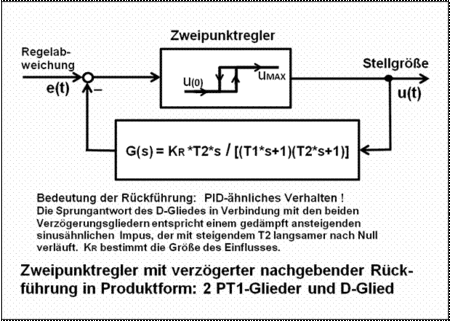
- Dies ist eine andere Variante eines Zweipunktreglers mit PID-ähnlichem Verhalten. Die Rückführung besteht aus 2 PT1-Gliedern und einem D-Glied, wobei das D-Glied und ein PT1-Glied die gleiche Zeitkonstante aufweisen.
- Das Ergebnis einer Sprungantwort dieser Rückführung nach einem positiven Eingangssprung ist ein einzelner gedämpft ansteigender sinusähnlicher Impuls, der exponentiell nach Null abfällt.
- Die Wirkung dieser beiden Verfahren der verzögert nachgebenden Rückführungen ist praktisch identisch. Lediglich die Parameter sind anders einzustellen.
- Übertragungsfunktion der Rückführung:
Testsignale zur Identifizierung des Zweipunktreglers
- Sprungantwort des Zweipunktreglers
- Anders als in der Klasse der stetigen Regler (Ausnahme P-Regler) haben alle Formen des Zweipunktreglers laut Definition im Signalflussplan als Sprungantwort scheinbar kein Zeitverhalten.
- Wenn ein vom negativen zum positiven Bereich kommendes Sprungsignal die eingestellte Hysterese des Reglers überwinden kann, springt das Ausgangssignal des Reglers auf den Schaltzustand UMAX. Dies ist unabhängig von der Größe einer vorhandenen zeitabhängigen Rückführung.
- Das übliche normierte Testsignal „Einheitssprung = 1“ und die zugehörige Sprungantwort ist deshalb keine Maßnahme zur Identifizierung des Verhaltens des Zweipunktreglers.
- Testsignal Wechselspannung
- Der Zweipunktregler ohne Hysterese reagiert auf die Amplituden der Wechselspannung im Nulldurchgang mit einer Rechteckspannung der Amplituden Umax gleicher Phasenlage. Bekommt der Regler eine symmetrisch wirkende Hysterese zugeordnet, reagiert er auf die Wechselspannung, wenn deren Amplitude größer als die Hysterese in % des Ausgangssignals Umax ist. Je nach Frequenz der Wechselspannung vergeht vom Nulldurchgang bis zur Überwindung der Hysterese eine Zeit, die eine nacheilende Phasenverschiebung der Rechtspannung verursacht.
- Testsignal Wechselspannung für Zweipunktregler mit Rückführung
- Rückführungen des Regler-Ausgangssignals mit zeitabhängigen Elementen wirken subtrahierend auf das Eingangssignal, um die Regelabweichung so zu verstimmen, dass der Regler vorzeitig ausschaltet. Damit wird im Regelkreis das Überschwingen der Regelgröße beim Erreichen des Sollwertes reduziert und die Schaltfrequenz erhöht. Eine verzögert nachgebende Rückführung reduziert zeitabhängig den Einfluss der dauernden Verstimmung der Regelabweichung.
- Mit einem Wechselspannungs-Testsignal kann das Arbeiten eines Zweipunktreglers und die Größe der Hysterese geprüft werden.
- Für die Ermittlung des Zeitverhaltens eines gegebenen Zweipunktreglers mit Rückführung mit einem symmetrischen Wechselspannungs-Testsignal muss der Mittelwert der Einschalt- und Ausschaltdauer während einer Periodendauer gebildet werden. Für hochwertige Regelungen der Genauigkeitsklasse < 1 % ist zu beachten, dass der Einfluss der Hysterese bei der Größenordnung < 1 % und der (vorübergehende) Einfluss der Rückführung bei der Größenordnung < 5 % liegt. Dieser Messvorgang ist schwierig.
- Die wirkliche qualitative Beurteilung des Verhaltens eines angepassten Zweipunktreglers und der benötigten Parameter für eine vorhandene Regelstrecke ist am einfachsten durch eine Simulation des Regelkreises möglich.
Dreipunktregler
Dreipunktregler mit 3 Schaltzuständen haben einen Eingang und 2 Ausgänge und schalten jeden der beiden Ausgänge in den Zustand „Ein“ oder „Aus“ oder „beide Aus“ in Abhängigkeit eines bestimmten positiven oder negativen Wertes des Eingangssignals e(t). Sie erlauben 2 unterschiedliche Energiearten zu schalten und haben eine meist symmetrische „Totzone“ mit einem oberen und unteren Grenzwert der Regelabweichung e(t), in der um den Nullpunkt der Regelabweichung keine Schaltaktivitäten stattfinden.
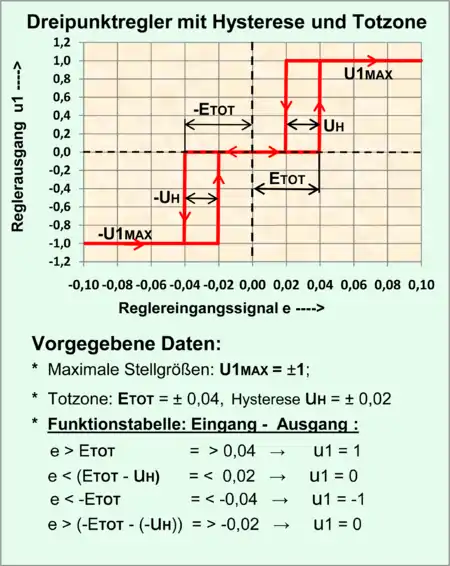
Anwendungen findet man häufig bei motorischen Stellantrieben für Vor- und Rücklauf und in allen Arten integral wirkenden Regelstrecken.
Bei proportionalen Regelstrecken mit unterschiedlichen dominanten Zeitkonstanten (Beispiel: schnelle Aufheizung und langsame Abkühlung) kann die Reaktionsgeschwindigkeit der Regelgröße für Führungsgrößenänderungen verbessert werden, wenn anstelle des Zweipunktreglers an einer Heizungsregelstrecke ein Kühlaggregat über einen Dreipunktregler eingeschaltet wird.
Andere Anwendungen des Dreipunktreglers mit unsymmetrischer Totzone sind bekannt zur Reduzierung der Schwankungsbreite der Regelgröße durch Regelung einer Grundlast mit aufgesetzter Teillast. Beispiel: Glühofen mit 2 Heizeinrichtungen.[9]
Ebenso wie bei dem Zweipunktregler kann der Dreipunktregler neben der Hysterese ein gewünschtes Zeitverhalten durch eine subtraktive Rückführung auf den Eingang des Reglers mit Verzögerungsgliedern bekommen.
Wie bei den Zweipunktreglern reduziert sich die Schaltfrequenz mit steigender Hysterese.
Die Größe der Totzone des Dreipunktreglers kann empirisch oder durch numerische Simulation bestimmt und optimiert werden. Sie ist von der Totzeit und von der Anzahl und Größe der Zeitkonstanten bzw. Integrationskonstanten der Regelstrecke abhängig. Eine weitere Vergrößerung einer als optimal bestimmten Totzone ruft bei P- und I-Regelstrecken größere Regelabweichungen gegenüber dem Sollwert hervor.
Systemgrößen des symmetrischen Dreipunktreglers
- UMAX und -UMAX entsprechen der maximalen und minimalen Stellgröße des Reglers,
- U1MAX und -U1MAX entsprechen der maximalen und minimalen Ausgangsgröße des Komparators. Für die Berechnung und Simulation des Regelkreises ist das Signal u1(t) vorteilhaft, wenn U1MAX und U1MIN der maximalen und minimalen Stellgröße zugeordnet werden.
- u1(t) beziehungsweise u(t) ist die modulierte Stellgröße des Dreipunktreglers, welche die Amplituden UMAX und -UMAX oder Null annehmen kann.
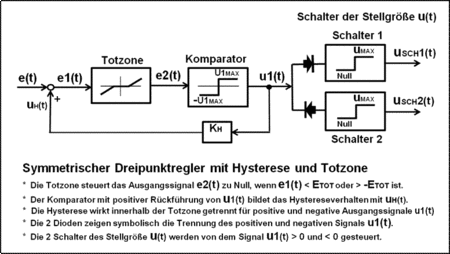
- Die Hysterese in % mit dem Einfluss uH(t) bezieht sich im positiven Bereich auf die Ausgangsgröße des Komparators UMAX und im negativen Bereich auf -UMAX. Laut dargestelltem Blockschaltbild und der Grafik mit der Funktionstabelle wirkt die Hysterese jeweils am Ende des positiven und negativen Bereichs der Totzone. Ist die Totzone gleich Null, wirken zwei getrennte Hysteresebereiche für positive und negative Reglerausgangsgrößen.
- Für die Einstellung der Hysterese muss das Verhältnis von UMAX zu U1MAX berücksichtigt werden. Der Faktor der Hysterese beträgt:
- Totzone ETOT
- Die Werte von ETOT und -ETOT beziehen sich auf einen Bereich des Eingangssignals e1(t), bei dem das Ausgangssignal e2(t) den Wert Null annimmt. Die Dimensionierung der Totzone ist abhängig von der Art der Regelstrecke.
- Die Stellgröße eines Dreipunktreglers in Verbindung mit einer P-Regelstrecke schwingt immer im positiven Bereich, wenn die Totzone optimiert wurde. Eine zu große Totzone vergrößert die stationäre Regelabweichung der Regelgröße.
- Je höher die Ordnung einer I-Regelstrecke ist und je größer die Totzeit, umso größer muss die Totzone gewählt werden, damit die Regelgröße auch innerhalb des Toleranzbereichs in den stationären schaltfreien Zustand kommt. Die Totzone wirkt erst, wenn UTOT > des Anteils der Hysterese uH(t) ist.
- In der Anwendung bei einem Regelkreis ist die Wirkung der Totzone erheblich größer als die der Hysterese. Die Totzone wird an das Einschwingverhalten der Regelgröße angepasst.
Numerische Beschreibung des Dreipunktreglers mit Hysterese und Totzone
- Einfluss der Hysterese uH: (Symmetrie der Komparatorsignale U1MAX und -U1MAX vorausgesetzt)
- Totzone (2 nichtlineare Gleichungen und deren Addition):
- Komparator mit Hystereserückführung
- In der Fachliteratur ist die übliche zeitunabhängige Darstellung des Ausgangssignals u als Funktion des Eingangssignals e des Dreipunktreglers als positives oder negatives Signal für den aktiven Zustand gezeichnet. Diese Form des Ausgangssignals mit den Amplituden U1MAX und -U1MAX ist für die Berechnung und Simulation des Regelkreises vorteilhaft.
- Ausgangsgröße des Komparators:
- Hystereseanteil:
- In der Realität sind dem laut Signalflussplan dargestellten Ausgangssignal u1(t) 2 unabhängige Schalter nachgeschaltet, welche die Schnittstelle der Regelstrecke mit den Schaltern USCH1 und USCH2 steuern. Die geschalteten Signale entsprechen U1MAX und -U1MAX.
Mehrpunktregler
Bei Mehrpunktreglern, zu denen auch der Dreipunktregler gehört, kommen noch zusätzliche Schaltzustände hinzu. Die Anwendung des Mehrpunktreglers setzt eine entsprechende Schnittstelle der Regelstrecke voraus.
Realisierung von Reglern
Analogregler und Digitalregler
- Analogregler
- Analoge Regler verarbeiten kontinuierliche Signale, diese können theoretisch beliebig fein aufgelöst werden.
- Sie werden meist mit Operationsverstärkern und einer auf die regeltechnische Aufgabe bezogenen RC-Beschaltung (Widerstand-Kondensator-Beschaltung) realisiert. Bei technischen Anlagen, in denen elektrische Energie nicht zur Verfügung steht oder Explosionsschutz erforderlich ist, werden auch pneumatische oder hydraulische Regler eingesetzt.
- Digitalregler mit Signalquantisierung
- Die dem Regler zugeführte kontinuierliche Signalgröße wird mittels eines Analog-Digital-Umsetzers digitalisiert. Ein Mikrocontroller kann z. B. den PID-Regelalgorithmus umsetzen. Die digitale Ausgangsgröße des Reglers (Schnittstelle) muss dem Stellglied der Regelstrecke angepasst werden. Analog wirkende Stellglieder können mit einem Digital-Analog-Umsetzer angesteuert werden oder auch zunehmend mit hochfrequenter Pulsweitenmodulation.
- Digitale Regler haben den Vorteil einer universellen Anpassung an die unterschiedlichsten Regelaufgaben, jedoch verlangsamen sie den Regelungsprozess durch die Digitalisierung der Regelgröße und die benötigte Rechenzeit bei schnellen Regelstrecken. Heute verfügbare Microcontroller unterstützen Auflösungen von 12 Bit (d. h. 4096 Stufen) oder mehr mit Abtastrasten von 1 MHz und erlauben die Berechnung eines PID-Algorithmus in weniger als 100 μs.[10] Sie sind damit für die meisten technischen Regelstrecken mehr als ausreichend schnell.
Kompaktregler
Kompaktregler sind zumeist digitale Kleinrechner mit eigenen, genormten elektrischen Ein- und Ausgängen zur Montage auf Hut-Schienen oder als Schalttafeleinbau.
Softwareregler in Prozessleitsystemen
Bei Softwarereglern wird das Computerprogramm als Soft-SPS in einem hinreichend leistungsfähigen Prozessleitsystem (PLS) realisiert. Die Ausführung des Codes erfolgt in deterministischer Echtzeit. Der Regler benötigt keine direkte Verdrahtung zu Sensoren und Aktoren, sondern kommuniziert mit beliebigen an das PLS angeschlossenen Aktoren und Sensoren, zum Beispiel über ein Feldbussystem wie Profibus, EtherCAT, Interbus, Foundation Fieldbus, AS-Interface. Dieses Vorgehen vermindert den Verkabelungsaufwand und erleichtert eine örtliche Trennung von Prozess und Regler.
Universalregler
Regler werden in vielen Anwendungsbereichen eingesetzt. Oft sind sie in Geräten eingebaut zum Beispiel der Zweipunktregler im elektrischen Bügeleisen, oder einer Schaltung zur Spannungsstabilisierung in einem Netzteil. Diese Regler sind meist speziell für das entsprechende Gerät entwickelt und gestatten keine Parameterveränderungen. In der Prozesstechnik, z. B. in der Chemieindustrie, in Kraftwerke oder in der Nahrungsmittelindustrie, werden Universalregler eingesetzt mit flexibler Einstellbarkeit der Reglerparameter
- Proportionalbeiwert,
- Nachstellzeit und
- Vorhaltzeit
so dass man sie als P-, PI-, PD- oder PID-Regler betreiben kann.
Ein Universalregler hat genormte Ein- und Ausgangssignale, sogenannte Einheitssignale. Das Eingangssignal kommt aus dem Messsystem und das Ausgangssignal wirkt auf das Stellglied. So ist es möglich, Geräte verschiedener Hersteller in einem Regelkreis miteinander zu betreiben. Live Zero (lebender Nullpunkt) bzw. offset zero bedeutet, dass das Einheitssignal einen Wert, zum Beispiel 4 mA, hat, wenn der Messwert 0 ist. Ist das Einheitssignal 0 mA, muss also ein Drahtbruch oder ein Kurzschluss vorliegen. Bei elektrischen Einheitssignalen werden Stromsignale bevorzugt. Sie sind bei langen Signalleitungen weniger anfällig gegen äußere Störfelder. Außerdem hat der Spannungsabfall an der Signalleitung keine Auswirkungen auf das Signal.
Pneumatischer Regler
Pneumatische Regler arbeiten mit genormten pneumatischen Ein- und Ausgängen, zum Beispiel 0,2 … 1 bar oder 3 … 15 psi. In der Verfahrenstechnik werden sie zum Beispiel im Explosionsschutz-Bereich eingesetzt.
Regler ohne Hilfsenergie
Regler ohne Hilfsenergie, häufig als ROH bezeichnet, übernehmen alle zur Regelung erforderlichen Aufgaben. Sie integrieren den Messaufnehmer, den Regler und auch das Stellglied in ein System und nehmen die Energie zum Arbeiten aus dem zu regelnden Medium. Beispiele sind der Druckregler eines Druckminderers für Gasflaschen und der Bimetallthermostat eines Bügeleisens.
Siehe auch
- Portal: Mess-, Steuerungs- und Regelungstechnik
Literatur
- M. Horn, N. Dourdoumas: Regelungstechnik. Pearson Studium, 2006, ISBN 3-8273-7260-7.
- O. Föllinger: Regelungstechnik, Einführung in die Methoden und ihre Anwendung. Hüthig Verlag, 1994, ISBN 3-7785-2336-8.
- G. Schulz: Regelungstechnik 1: Lineare und Nichtlineare Regelung, Rechnergestützter Reglerentwurf. 3. Auflage. Oldenbourg, München 2007, ISBN 978-3-486-58317-5.
- M. Reuter, S. Zacher: Regelungstechnik für Ingenieure: Analyse, Simulation und Entwurf von Regelkreisen. 12. Auflage. Vieweg+Teubner, 2008, ISBN 978-3-8348-0018-3.
- J. Lunze: Regelungstechnik 1 – Systemtheoretische Grundlagen, Analyse und Entwurf einschleifiger Regelungen. Springer-Verlag, 2006, ISBN 3-540-28326-9.
- H. Unbehauen: Regelungstechnik 1. Vieweg Verlag, 2007, ISBN 978-3-528-21332-9.
- H. Lutz, W. Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink. 12. Auflage. Europa-Verlag, 2021, ISBN 978-3-8085-5870-6.
- H. Töpfer, W. Kriesel: Kleinautomatisierung durch Geräte ohne Hilfsenergie. (Automatisierungstechnik, Band 173). Verlag Technik, Berlin 1976, 2. Auflage 1978 (mit Ekkehard Reimann und Mertik Quedlinburg).
- H. Töpfer, W. Kriesel: Funktionseinheiten der Automatisierungstechnik - elektrisch, pneumatisch, hydraulisch. Verlag Technik Berlin, VDI-Verlag, Düsseldorf 1977, 5. Auflage 1988, ISBN 3-341-00290-1.
- Erwin Samal, Dirk Fabian, Christian Spieker: Grundriss der praktischen Regelungstechnik. Oldenbourg Verlag, 2013, ISBN 3-486-71290-X.
Weblinks
- Regelungstechnik im Roboternetz-Wiki
- Regelungstechnisches Beispiel: Toilettenspülung
- Einführung in die ROH-Technik (PDF; 274 kB)
Einzelnachweise
- PID Control History and Advancements. 2013, abgerufen im Jahr 2020 (englisch).
- Lutz, Wendt: Taschenbuch der Regelungstechnik, Kapitel: Regelung durch Zustandsrückführung.
- Oliver Nelles: Vorlesungskonzept Mess- und Regelungstechnik II. Universität Siegen. Kapitel: „Beschreibung dynamischer Systeme im Zustandsraum“ vom 4. Mai 2010.
- Manfred Reuter, Serge Zacher: Regelungstechnik für Ingenieure, Kapitel „Mehrgrößenregelung“
- Oliver Nelles: Vorlesungskonzept Mess- und Regelungstechnik II. Universität Siegen. Kapitel: „Mehrgrößenregelung“ vom 4. Mai 2010.
- H. Peter Jörgl: Vorlesungsmanuskript Mess- und Regeltechnik VT. TU Wien, Institut für Prozessautomatisierung, SS 2006, Kapitel Mehrgrößenregelung.
- Reuter, Zacher: Regelungstechnik für Ingenieure. Kapitel „Zweipunktregler mit Rückführung“.
- Lutz, Wendt: Taschenbuch der Regelungstechnik, Kapitel „Quasistetige Standardregler mit Rückführung“.
- Gerd Schulz: Regelungstechnik 1, Kapitel „Dreipunktregler mit Hysterese“.
- Neue STM32-Mikrocontroller für digitale Regler. In: elektroniknet.de. 5. Juni 2019, abgerufen am 3. August 2019.