Modell
Ein Modell ist ein vereinfachtes Abbild der Wirklichkeit. Das Abbild kann die Form konkreter Gegenstände haben (Modell-Eisenbahn, Computersimulation u. ä.) oder rein abstrakt dargestellt sein (Theorien; Gleichungen). Nach Herbert Stachowiak kennzeichnen ein Modell mindestens drei Merkmale:[1]
- 1. Abbildung
- Ein Modell steht immer für etwas anderes – nämlich für ein natürliches oder ein künstliches Original, welches es somit abbildet oder repräsentiert. Von Modellen lassen sich ihrerseits Modelle anfertigen, in denen somit das Original z. B. um noch einen Schritt weiter vereinfacht repräsentiert ist. Beispiel für einen partiellen Komplexizitätszuwachs ist die Ausschnittsvergrößerung einer Technischen Zeichnung.
- 2. Verkürzung
- Ein Modell erfasst nicht alle Attribute des Originals, sondern nur diejenigen, die dem Modellschaffer bzw. Modellnutzer relevant erscheinen.
- 3. Pragmatismus
- Modelle sind ihren Originalen nicht eindeutig zugeordnet. Sie erfüllen ihre Ersetzungsfunktion
- a) für bestimmte Subjekte (für wen?)
- b) innerhalb bestimmter Zeitintervalle (wann?)
- c) unter Einschränkung auf bestimmte gedankliche oder tatsächliche Operationen (wozu?).
Zudem werden gelegentlich weitere Merkmale diskutiert, wie Extension und Distortion[2] sowie Validität.[3] Der amerikanische Wissenschaftsphilosoph Michael Weisberg unterscheidet auf der obersten Ebene zwischen gegenständlichen (concrete) und mathematischen Modellen und stellt daneben die Computersimulationen (computational models) als eigene Klasse von Modellen auf.[4]
Wortherkunft
Das Wort Modell entstand im Italien der Renaissance als ital. modello, hervorgegangen aus lat. modulus, einem Maßstab in der Architektur, und wurde bis ins 18. Jahrhundert in der bildenden Kunst als Fachbegriff verwendet. Um 1800 verdrängte Modell im Deutschen das ältere, direkt vom lat. modulus (Maß(stab)) entlehnte Wort Model (Muster, Form, z. B. Kuchenform), das noch im Verb ummodeln und einigen Fachsprachen und Dialekten fortlebt.
Modellbildung
Die Modellbildung abstrahiert mit dem Erstellen eines Modells von der Realität, weil diese meist zu komplex ist, um sie vollständig abzubilden. Diese Vollständigkeit wird aber auch gar nicht beabsichtigt, vielmehr sollen lediglich die wesentlichen Einflussfaktoren identifiziert und dargestellt werden, die für den realen Prozess und im Modellkontext bedeutsam sind.
Man unterscheidet die strukturelle und die pragmatische Modellbildung.
- Bei struktureller Modellbildung ist die innere Struktur des Systems bekannt, es wird jedoch bewusst abstrahiert, modifiziert und reduziert. Man spricht hier von einem ‚Whitebox-Modell‘.
- Bei pragmatischer Modellbildung ist die innere Struktur des Systems unbekannt, es lässt sich nur das Verhalten bzw. die Interaktion des Systems beobachten und modellieren. Die Hintergründe lassen sich meist nicht oder nur zum Teil verstehen – hier spricht man von einem ‚Blackbox-Modell‘.
- Zudem gibt es Mischformen, bei denen Teile des Systems bekannt sind, andere wiederum nicht. Nicht alle Wechselwirkungen und Interaktionen zwischen Teilkomponenten lassen sich nachvollziehen – hier spricht man vom ‚Greybox-Modell‘. Diese Mischform ist die häufigste, weil es aufgrund von Kosten-Nutzen-Überlegungen meist ausreichend ist, das System auf diese Weise abzubilden.
Prozesse der Modellbildung:
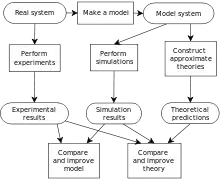
Bei der Modellbildung lassen sich folgende Prozesse differenzieren:
- Abgrenzung
- Nichtberücksichtigung irrelevanter Objekte
- Reduktion
- Weglassen von Objektdetails
- Dekomposition
- Zerlegung, Auflösung in einzelne Segmente
- Aggregation
- Vereinigung, Zusammenfassen von Segmenten zu einem Ganzen
- Abstraktion
- Begriffs- bzw. Klassenbildung
Komplexität und Qualität eines Modells
Ein Ziel eines Modellierers ist generell die Reduzierung der Komplexität des Modells gegenüber der Realität. Ein häufiger Trugschluss ist daher, ein Modell mit der Realität gleichzusetzen. Tatsächlich kann lediglich der Modellkontext bestimmt und optimiert werden.[5] Damit wird die Zweckbindung des Modells bestimmt. Weiter kann das Modell hinsichtlich der Komplexität variiert werden.[6] Im Grundsatz bleibt das Modell in allen Merkmalen außer der Verständlichkeit immer hinter der Realität zurück.
Modelle in verschiedenen Kategorien
Jede Wissenschaftsdisziplin hat ihre eigenen Modellsystematiken. Diese ändern sich mit der laufenden Entwicklung in der jeweiligen Kategorie und folgen neuen Schwerpunkten auch mit Verzweigungen solcher Systematik. Die Mathematisierung einzelner Wissenschaftszweige, wie der Betriebswirtschaftslehre (Prognoseverfahren), der Volkswirtschaftslehre (Simulationsverfahren) oder der Biologie (Gentechnik) eröffneten völlig neue Modellwelten.
Mathematische Modelle in der Wissenschaft
Mathematische Modelle sind in mathematischen Formeln beschriebene Modelle. Sie versuchen, die wesentlichen Parameter der meist natürlichen Phänomene zu erfassen. Durch die formelle Beschreibung kann ein Modell berechnet und wissenschaftlich geprüft werden.
Berechenbarkeit bedeutet hier sowohl die analytische Untersuchung als auch die Approximation mittels numerischer Verfahren. In der Regel sind auch die sogenannten physikalischen Modelle mathematische Modelle, sie stützen sich jedoch auf physikalische Gesetzmäßigkeiten.
Ein valides Modell kann zur Prognose eines zukünftigen Verhaltens benutzt werden.
Bekannte Anwendungsfälle mathematischer Modelle sind etwa Prognosen des Klimawandels, des Wetters oder die Statik eines Gebäudes.
Oft werden bei mathematischen Modellen Empirische Funktionen verwendet.
Mathematik und Logik
In der Modelltheorie der mathematischen Logik geht es nicht um eine Abbildung der Wirklichkeit in Mathematik. Hier versteht man unter einem Modell eines Axiomensystems eine mit gewissen Strukturen versehene Menge, auf die die Axiome des Systems zutreffen. Die Existenz eines Modells beweist, dass sich die Axiome nicht widersprechen; existieren sowohl Modelle mit einer gewissen Eigenschaft als auch solche, die diese Eigenschaft nicht haben, so ist damit die logische Unabhängigkeit der Eigenschaft von den Axiomen bewiesen.
In der Logik ist das Modell einer Formel F eine Bewertung, die F den Wahrheitswert <wahr> zuordnet. Man spricht auch davon, dass diese Bewertung die Formel erfüllt.[7] Das Modell eines Satzes (einer Formel) ist daher eine Interpretation, die den Satz (die Formel) erfüllt.
Entsprechend ist das Modell einer Menge wohlgeformter Formeln die Interpretation durch Zuordnung von semantischen Werten zu den in den Formeln enthaltenen einfachen Ausdrücken, so dass alle Formeln den Wahrheitswert <wahr> erhalten,[8] also eine Belegung, die die betreffende Menge verifiziert. Abstrakter kann man formulieren, dass wenn „Σ eine Menge von L-Sätzen [ist]; eine L-Struktur, die jeden Satz in Σ wahr macht, […] ein Modell von Σ [heißt].“[9]
Das Modell eines Axiomensystems ist ein Gegenstandsbereich und eine Interpretation der undefinierten Grundbegriffe, bei der ein Axiomensystem wahr ist[10] oder mit den Worten Carnaps:
„Unter einem Modell (genauer, einem logischen oder mathematischen Modell) für die axiomatischen Grundzeichen eines gegebenen AS (Axiomensystems) in Bezug auf einen gegebenen Individuenbereich D versteht man eine Bewertung für diese Zeichen derart, dass sowohl der Bereich D wie auch die Bewertung ohne Gebrauch deskriptiver Konstanten angegeben wird.“[11]
Mit anderen Worten heißt es im Historischen Wörterbuch der Philosophie: „Modell heißt in der Logik ein System aus Bereichen und Begriffen, insofern es die Axiome einer passend formulierten Theorie erfüllt.“
In der Modallogik besteht ein Modell aus drei Komponenten:
- einer Klasse möglicher Welten;
- einer Zuordnungsfunktion, die jedem Paar aus einer atomaren Aussage und einer möglichen Welt einen Wahrheitswert zuordnet;
- einer Zugänglichkeitsrelation zwischen möglichen Welten.[12]
Die Modelltheorie der Logik wird auch in der modelltheoretischen Semantik verwandt.
Wissenschaftstheorie
In der Methodologie und Wissenschaftstheorie wird zwischen Modellen unterschieden, die zur Erklärung von bekannten Sachverhalten oder Objekten dienen und solchen, die auf einer hypothetischen Annahme (Hypothese) beruhen und bei denen der Entdeckungszusammenhang beim Test von Theorien im Vordergrund steht. Erklärende Modelle sind häufig Skalenmodelle, die einen maßstäblichen Bezug zur Wirklichkeit haben (Spielzeugauto). Demgegenüber stehen Analogiemodelle, die die Strukturähnlichkeit (Homomorphie) der abgebildeten Wirklichkeit erzeugen (sollen) wie zum Beispiel das Planetenmodell der Atome. Für Theorien werden oftmals abstrakte oder fiktive Modelle gebildet. Eine weitere Unterscheidung ist, ob Modelle beschreibend sind (deskriptiv) oder ob durch die Modelle ein Sachverhalt festgelegt wird (präskriptiv).
Dem Modell kommt im wissenschaftlichen Erkenntnisprozess eine große Bedeutung zu. Unter bestimmten Bedingungen und Zwecksetzungen besitzen Modelle bei der Untersuchung realer Gegenstände und Prozesse in unterschiedlichen Wirklichkeitsbereichen und beim Aufbau wissenschaftlicher Theorien eine wichtige Erkenntnisfunktion. So dienen sie u. a. dazu, komplexe Sachverhalte zu vereinfachen (idealisieren) bzw. unserer Anschauung zugänglich zu machen.
Fiktive Modelle sind Mittel zur tieferen und umfassenderen Erkenntnis der Wirklichkeit. Im Prozess der Abstraktion mit Methoden der Idealisierung bzw. der Konstruktion entstanden, helfen sie, reale Eigenschaften, Beziehungen und Zusammenhänge aufzudecken, bestimmte reale Eigenschaften erfassbar und praktisch beherrschbar werden zu lassen. Sie werden zumeist gebildet, um auf real existierende Objekte die Mittel der theoretischen, besonders der mathematischen Analyse anwenden zu können.
Beispiele: ideales Gas, absolut schwarzer Körper, Massenpunkt, vollkommener Markt u. a. (siehe ideales Objekt)
Die erkenntnistheoretische und logische Möglichkeit und Rechtfertigung der Zulässigkeit von Modellen ist nur eine Seite. Wesentlich ist letztlich die Rechtfertigung der Zulässigkeit der Fiktion durch die tätige Praxis, das heißt der praktische Nachweis, dass die mit Hilfe des Modells aufgebaute Theorie auf reale Objekte effektiv angewendet werden kann.
Eine gesonderte Diskussion wird in der Wissenschaftstheorie darüber geführt, ob Modelle als Repräsentationen die Realität abbilden (Realismus), oder ob es sich nur um theoretische Konstruktionen handelt (Konstruktivismus).
Sozial- und Kulturwissenschaften
In den Sozialwissenschaften wird der Begriff des Modells nicht erst seit Niklas Luhmann vielfältig verwendet. Zum Beispiel wird ein Theoriegebäude zur Analyse und Planung von Unterricht als ein „didaktisches Modell“ bezeichnet. Dieser Sprachgebrauch beruht auf der modellhaften Analogie, dass in der Entwicklung einer Handlungsanleitung die methodischen Schritte Formulierung, Erprobung, Validierung aufeinander folgen.
Für den Anthropologen Edward T. Hall[13] umfasst eine Kultur eine Reihe von situationsspezifischen Modellen des Verhaltens und des Denkens ihrer Mitglieder. Diese Modelle können wiederum von Ethnologen und Anthropologen hochgradig abstrakt beschrieben werden (z. B. in Form eines Verwandtschaftsmodells). Aber auch solche Modelle des Denkens können durchaus reale Wirkungen implizieren (Theoreality).
Max Weber sprach vom Idealtypus in der sozialwissenschaftlichen Forschung und meinte damit nichts Anderes als ein abstraktes, idealisiertes Modell der Realität. Ein Idealtypus kann sowohl gesellschaftliche Strukturen (Demokratie oder mittelalterliche Stadt) als auch zeitliche Verläufe (Revolutionen oder Konjunkturmodelle) beschreiben.
In der Wirtschaftswissenschaft dienen Modelle zur Beschreibung und Untersuchung von ökonomischen Strukturen und Prozessen. Zu den wichtigsten Annahmen für Modelle in der VWL gehören der vollkommene Markt und der Homo oeconomicus. Modelle können unter anderem nach folgenden Gesichtspunkten eingeteilt werden:
- dem Einsatzzweck (Beschreibungs-, Erklärungs-, Prognose-, Entscheidungs- oder Simulationsmodelle)
- dem Grad der Abstraktion (deterministische oder stochastische Modelle)
- statische und dynamische Modelle (mit diskreter bzw. kontinuierlicher Zeitberücksichtigung)
- Partial- und Totalmodelle (Modulation von realen Systemen in Teilen oder in seiner Gesamtheit)
- Stationäre Modelle und Wachstumsmodelle: Diese Unterscheidung ist zwar der Ersteren ähnlich, bezieht sich aber auf die Modelle der Konjunkturtheorie. Im Gegensatz zu den Wachstumsmodellen kennen die stationären Modelle keine Auf- und Abschwünge
- Mikroökonomische und makroökonomische Modelle: Die Ersteren werden häufig zur Fundierung makroökonomischer Aussagen benutzt
Psychologie
In der Psychologie werden verschiedene „Modelle des Menschen“ unterschieden. Es handelt sich hierbei um Paradigmen, die sich in den Grundannahmen und der Methodologie unterscheiden.
Der Modellbegriff spielt weiterhin in der Lerntheorie eine zentrale Rolle; auch die Pädagogische Psychologie thematisiert diese Lernform (siehe Lernen, Beobachtungslernen, Modelllernen, Imitationslernen, Lernen am Vorbild). Die Theorie vom Modelllernen oder vom Lernen am Modell erläutert, wie Verhalten zustande kommt, nämlich durch die Nachahmung des Verhaltens, das eine Person (das Modell) realisiert hat. Dabei spielt es z. B. eine Rolle, welches Verhältnis der Nachahmende zum Modell (Eltern, Lehrer, Erzieher usw.) hat oder wie erfolgreich ein Modell sein Verhalten (in sozialen Situationen) gestalten kann bzw. welches gesellschaftliche Ansehen ein Modell zeigt. Man kann davon ausgehen, dass insbesondere komplexe Verhaltensketten im sozialen Umfeld durch Nachahmungslernen zustande kommen.[14]
Grundsätzlich hat die Lernforschung herausgefunden:
- Haben Lernender und Modell ein gutes Verhältnis, werden Verhaltensweisen leichter übernommen. Der Zusammenhang spielt in Erziehungsprozessen eine herausragende Rolle.
- Ist das Modell selbst erfolgreich in diversen sozialen Situationen, wird auch sein Verhalten von Lernenden leichter übernommen.
- Modelle mit höherem Sozialprestige sind in der Regel wirksamer, was die Übernahme von Verhalten angeht.
- Übernommenes Verhalten, das in seiner sozialen Umgebung erfolgreich ist, wird vom Lernenden eher beibehalten (s. auch Lernen: operantes Konditionieren; Verstärkungslernen).
- Beobachtetes und nachgeahmtes Verhalten von großer Bedeutung (für den Nachahmer) wird eher beibehalten als Verhalten mit minderer Bedeutung.
- Unsichere und ängstliche Personen sind eher bereit, Verhalten von Modellen zu übernehmen.[15]
Feldtheorie: Der Psychologe Kurt Lewin (1890–1947) war ein großer Meister im Entwerfen von Modellen für komplexe Sachverhalte in der Psychologie (Feldtheorie in den Sozialwissenschaften, Bern 1963), etwa in den motivationspsychologischen Arbeiten.
Pädagogik
Die Frage nach dem Modell ist in der Pädagogik vor allem die Frage nach dem Selbstverständnis des Erziehenden. (In der Alltagssprache verwendet man eher das Wort Vorbild.) Der agierende Erzieher muss sich die Frage gefallen lassen, ob er exakt das in seinem Verhalten realisiert, was er theoretisch und praktisch in Erziehungssituationen als angemessen bis optimal zu fordern bereit ist, um als Modell (Vorbild) fungieren zu können. Ist er nicht dazu bereit oder nicht in der Lage, mangelt es ihm nach allgemeinem Verständnis an Glaubwürdigkeit. Ein Erziehender, der vom Kind/Jugendlichen z. B. Vertrauen fordert, selbst aber kleinlich auf die Einhaltung von Vorschriften aus ist, die er womöglich selbst formuliert hat, produziert einen Widerspruch zwischen seinen Forderungen und dem konkreten Verhalten. Als Modell wäre er damit zutiefst unglaubwürdig.[16]
Erziehende, die viele Widersprüche dieser Art aufweisen, können in ihrer Tätigkeit nicht erfolgreich sein, da sie unweigerlich Konflikte mit den Kindern und Jugendlichen hervorrufen, die sie überdies schwer erklären oder rechtfertigen können. Glaubwürdiges Modell zu sein, erfordert viel Selbstkritik und Reflexion seiner Tätigkeit.
Das glaubhafte Modell bildet also der Erzieher, der seine Werte, Erziehungsvorstellungen und Lehren nicht nur verbal vertritt, sondern für alle sichtbar lebt – vorerst einmal unabhängig davon, welche pädagogische Ideologie er vertritt. Da man nicht voraussetzen kann, dass ein Erziehender gänzlich ohne Fehl und Tadel wirken kann, müsste man in diesem Sinne einen Erzieher fordern, der seine internen Widersprüche auf ein akzeptables Maß reduziert, um ein glaubhaftes Modell werden zu können. Ein professionell handelnder Erzieher kann nur der sein, der seine Widersprüche zu reflektieren bereit und imstande ist.
Ein Modell (Vorbild) von historischem Ausmaß etwa war Janusz Korczak, der mit den Kindern aus seinem Kinderheim im Warschauer Ghetto in die Gaskammer ging, obwohl ihm die Nazis angeboten hatten, er müsse die Waisen nicht begleiten. Er entschied sich aber dafür, die Kinder bei ihrem letzten Gang nicht allein zu lassen.
Informatik
In der Informatik dienen Modelle zum einen zur Abbildung eines Realitätsausschnitts, um eine Aufgabe mit Hilfe der Informationsverarbeitung zu lösen. Derartige Modelle heißen Domänenmodelle. Hierunter fallen z. B. Modelle für zu erstellende Software sowohl für deren Architektur (Architekturmodell) als auch deren Code (in Form von beispielsweise Programmablaufplandiagrammen) und Datenmodelle für die Beschreibung der Strukturen von zu verarbeitenden Daten aus betrieblicher/fachlogische Sicht oder aus technischer Datenhaltungssicht. Zum anderen können Modelle als Vorlage bei der Konzeption eines informatorischen Systems dienen, man spricht dann von Modellsystemen. Hierunter fallen insbesondere Referenzmodelle, die allgemein als Entwurfsmuster eingesetzt werden können. Referenzmodelle werden beispielsweise für die Konzeption konkreter Computerarchitekturen, Netzwerkprotokolle, Anwendungssysteme, Datenhaltungssysteme und Portale herangezogen.
Neben diesen Modellen, die sich in Hard- und Software sowie in Datenbeständen konkretisieren, gibt es auch Planungs-, Steuerungs- und Organisationsmodelle. Typische zu modellierende Objekte sind hierbei die Ablaufstruktur eines Geschäftsprozesses, abgebildet in einem Geschäftsprozessmodell, und die Aufbaustruktur einer betrieblichen Organisation, abgebildet in einem Organigramm. (Lit.: Broy)
In der Wirtschaftsinformatik dienen Modelle vorwiegend der Beschreibung realer und soziotechnischer Systeme, siehe Modell (Wirtschaftsinformatik). Bei der Modellierung von Mensch-Maschine-Systemen – eine Domäne der Wirtschaftsinformatik – muss die technische wie auch die menschliche Komponente modelliert werden. Für den Menschen stehen unterschiedliche Modelle zur Verfügung, die verschiedene Aspekte menschlichen Verhaltens und menschlicher Fähigkeiten nachbilden und die entsprechend dem Untersuchungsziel ausgewählt werden. Fahrermodelle oder Pilotenmodelle modellieren den Menschen in einer ganz bestimmten Arbeitssituation, Regler-Mensch-Modelle in seiner allgemeinen Fähigkeit, eine Größe zu regeln. Die Anpassungsfähigkeit des Menschen an kognitiv unterschiedlich anspruchsvolle Aufgaben wird im Drei-Ebenen-Modell nach Rasmussen nachgebildet. Ein Gegenstand der Forschung ist unter anderem, kognitive Architekturen wie ACT-R/PM oder SOAR in der anwendungsorientierten Modellierung und Simulation (MoSi) von Mensch-Maschine-Schnittstellen einzusetzen.
Spezielle Wortverwendungen
- Ein Computermodell ist ein mathematisches Modell, das aufgrund seiner Komplexität und/oder der schieren Anzahl von Freiheitsgraden nur mit einem Computer ausgewertet werden kann.
- In der Computergrafik und verwandten Gebieten werden mit Hilfe der geometrischen Modellierung 3D-Modelle von Körpern erzeugt.
- Ein Digitales Geländemodell (DGM) bzw. Digitales Höhenmodell (DHM) ist ein digitales, numerisches Modell der Geländehöhen und -formen. Ein DGM bzw. DHM stellt im Gegensatz zum Digitalen Oberflächenmodell (DOM) keine Objekte auf der Erdoberfläche dar (z. B. Bäume oder Häuser).
Naturwissenschaften: Chemie und Physik
In der Chemie dienen Modelle insbesondere zur Veranschaulichung von kleinsten Teilchen, wie beispielsweise Atome und Moleküle, und zur Erklärung und Deutung von chemischen Reaktionen, die oftmals auch simuliert werden. Modellexperimente stellen häufig die Funktion von technischen Prozessen dar.
In der Physik spielen Modelle ähnlich wie in der Chemie zur Veranschaulichung und zum Verständnis von Atomen und Elementarteilchen eine große Rolle. Physikalische Theorien und Modelle sind eng verknüpft und bestimmen das Denken in Modellen zur Erkenntnisgewinnung und zum Verständnis von Relationen und Strukturen. Beispiele für Theorien sind die Atomtheorie, die kinetische Gastheorie, die Wellentheorie des Lichts und die Relativitätstheorie. Zur Modellbildung gehört auch die Mathematisierung physikalischer Gesetzmäßigkeiten. Im didaktischen Bereich werden Modelle häufig im Sinne von Analogien zwischen dem zu untersuchenden Objektbereich und schon erforschten Bereichen benutzt. Zusätzlich werden Demonstrationsmodelle als vereinfachte Abbilder (z. B. das Planetenmodell) benutzt. Simulationen dienen neben der Veranschaulichung physikalischer Zusammenhänge der Überprüfung von Hypothesen. Experimente haben nicht nur im Physikunterricht oft Modellcharakter, indem sie die komplexe Realität vereinfachen und sich bei der induktiven Herleitung von Gesetzmäßigkeiten auf das Wesentliche beschränken. Funktionsmodelle haben beispielsweise eine Bedeutung zur Verdeutlichung der Funktion von einfachen Maschinen.
Spezielle Ansätze
Modellplatonismus
Der Begriff wurde durch Hans Albert geprägt. Er kennzeichnet kritisch die Abweichung des neoklassischen Denkstils in der Volkswirtschaftslehre von der Methodologie einer empirischen Sozialwissenschaft.[17] Als Beispiele dienen das Nachfragegesetz, die Quantitätstheorie sowie die Wachstumstheorie.
Obwohl die neoklassische Theorie mit ihren Modellbetrachtungen offenkundig auf das wirtschaftliche Handeln von Menschen gerichtet ist, wird die soziale Verursachung des menschlichen Handelns, wie sie etwa die empirische Sozialwissenschaft auf unterschiedliche Weise in Rechnung stellt, größtenteils ausgeschaltet. Einige Theoretiker leugnen gar die Absicht, kausale Erklärungen zu liefern und begnügen sich anstelle von Aussagen, die Informationsgehalt besitzen, weil sie an empirischen Daten scheitern können, mit Aussagen, die nichts weiter als einen Realitätsbezug aufweisen (d. h. reale Dinge erwähnen). Verbunden wird diese Vorgehensweise mit der Tendenz, die Aussagen so zu gestalten, dass sie schon aufgrund ihrer logischen Struktur wahr sind. Erreicht wird dies durch tautologische Formulierungen oder die Anwendung von konventionalistischen Strategien (Immunisierungsstrategie), wozu zum Beispiel die Verwendung einer expliziten oder impliziten ceteris-paribus-Klausel rechnet. Dieser von ihren Anhängern in ihren praktischen Konsequenzen für die Anwendbarkeit der analytischen Ergebnisse nicht immer überblickte methodische Stil des Denkens in Modellen, die von jedweder empirischen Überprüfbarkeit bewusst oder unbewusst abgeschottet werden, läuft auf eine neuartige Form des Platonismus hinaus.[18] Platon war davon überzeugt, dass die Wirklichkeit durch rein logisches Denken erkannt werde; statt die Sterne zu beobachten, sollten wir deren Bewegungsgesetze durch das Denken ergründen.[19]
In der deutschen Nationalökonomie dominierte damals der Schulenstreit zwischen Begriffsrealismus (Essentialismus) und Modellplatonismus. Diese Frontstellung hält Albert für aus methodologischen Gründen verfehlt; er setzt sich stattdessen ein für Wirtschaftswissenschaft, verstanden als eine empirische Sozialwissenschaft. In diesem Sinne spricht er auch von Marktsoziologie oder einer „Soziologie der kommerziellen Beziehungen“.[20]
Literatur
- Wolfgang Balzer: Empirische Theorien: Modelle – Strukturen – Beispiele. Die Grundzüge der modernen Wissenschaftstheorie. Vieweg, Braunschweig 1982.
- Manfred Broy, Ralf Steinbrüggen: Modellbildung in der Informatik. Springer, Berlin / Heidelberg 2004, ISBN 3-540-44292-8.
- Hans Kleine Büning, Uwe Kastens: Modellierung. Hanser, 2005, ISBN 3-446-40460-0.
- Dietrich Dörner: Modellbildung und Simulation. In: E. Roth (Hrsg.): Sozialwissenschaftliche Methoden. Oldenbourg, München 1984, S. 337–350.
- Norbert Kühne u. a.: Psychologie für Fachschulen und Fachoberschulen. 8. Auflage. Bildungsverlag EINS, Troisdorf 2006, ISBN 3-427-04150-6.
- Kurt Lewin: Feldtheorie in den Sozialwissenschaften, Verlag Hans Huber, Bern 1963
- R. Mayntz: Modellkonstruktion: Ansatz, Typen und Zweck. In: R. Mayntz (Hrsg.): Formalisierte Modelle in der Soziologie. Luchterhand, Neuwied/Berlin 1967.
- Bernd Mahr: Modellieren, Beobachtungen und Gedanken zur Geschichte des Modellbegriffs. In: Sybille Krämer, Horst Bredekamp [Hrsg.]: Bild, Schrift, Zahl. München: Fink, 2003 (2. Aufl. 2009).
- Jürgen Perl, Martin Lames, Ulrich Glitsch (Hrsg.): Modellbildung in der Sportwissenschaft. Hofmann, Schorndorf 2002, ISBN 3-7780-1821-3 (Beiträge zur Lehre und Forschung im Sport, Band 132).
- Ingeborg Reichle, Steffen Siegel, Achim Spelten (Hrsg.): Visuelle Modelle. Wilhelm Fink, München 2008. ISBN 978-3-7705-4632-9.
- Magnus Richter: Zur Güte von Beschreibungsmodellen – eine erkenntnistheoretische Untersuchung. Ilmenau 2009.
- Magnus Richter: Modelle in der Betriebswirtschaftslehre – Ein systematischer Überblick über Merkmale, Ziele und Erscheinungsformen. In: WiSt – Wirtschaftswissenschaftliches Studium, Jg. 42, Nr. 6, 2013, S. 280–285.
- Reinhard Schütte: Grundsätze ordnungsmäßiger Referenzmodellierung. Gabler, Wiesbaden 1998, ISBN 3-409-12843-3.
- Herbert Stachowiak: Allgemeine Modelltheorie. Wien 1973, ISBN 3-211-81106-0.
- Herbert Stachowiak (Hrsg.): Modelle – Konstruktion der Wirklichkeit. Wilhelm Fink Verlag, München 1983, S. 17–86.
- Wolfgang Stegmüller: Carnap II: Normative Theorie des induktiven Räsonierens (= Probleme und Resultate … Band 4, C). Springer, 1973, ISBN 3-540-05991-1, S. 417 ff.
- Patrick Suppes: The Desirability of Formalization in Science. In: Journal of Philosophy, 65 (1968), S. 651–664; dt. Warum Formalisierung in der Wissenschaft erwünscht ist. In: W. Balzer, M. Heidelberger (Hrsg.): Zur Logik empirischer Theorien. Berlin 1983, S. 24–39.
- Reinhard Tausch, Anne-Marie Tausch: Erziehungspsychologie. 6. Auflage. Verlag für Psychologie Hogrefe, Göttingen 1971.
- K. Troitzsch: Modellbildung und Simulation in den Sozialwissenschaften. Westdeutscher Verlag, Opladen 1990.
- R. Ziegler: Theorie und Modell. Der Beitrag der Formalisierung zur soziologischen Theoriebildung. Oldenbourg, München 1972.
- Dietrich Zschocke: Modellbildung in der Ökonomie. Vahlen, München 1995, 2002, ISBN 3-8006-1962-8.
- Natascha Adamowsky (Hrsg.): Digitale Moderne. Die Modellwelten von Matthias Zimmermann. Hirmer Verlag, München 2018, ISBN 978-3-7774-2388-3
Weblinks
- Roland Müller: Modellgeschichte ist Kulturgeschichte, Eine Chronik von Modellgebrauch und Modellbegriff, 2000. (und weitere Materialien zum Gebrauch von Modellen als Veranschaulichungen seit der frühen Neuzeit)
- Sammlung mathematisch-geometrischer Modelle der Technischen Universität Dresden
- Objektdatenbank von materiellen Modellen in Forschung und Lehre am Helmholtz-Zentrum für Kulturtechnik der Humboldt-Universität zu Berlin
- Roman Frigg und Stephan Hartmann: Models in Science. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
- James Woodward: Scientific Explanation. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
- Jeffrey Koperski: Models. In: J. Fieser, B. Dowden (Hrsg.): Internet Encyclopedia of Philosophy.
Einzelnachweise
- Herbert Stachowiak: Allgemeine Modelltheorie, 1973, S. 131–133.
- Thalheim: Towards a Theory of Conceptual Modelling. In: Journal of Universal Computer Science, vol. 16, 2010, no. 20, S. 3120
- Dietrich Dörner: Thought and Design – Research Strategies, Single-case Approach and Methods of Validation. In: E. Frankenberger u. a. (Hrsg.): Designers. The Key to Successful Product Development. Springer-Verlag, Berlin u. a. 1998, S. 3–11.
- M. Weisberg: Simulation and Similarity - using models to understand the world. Oxford University Press, New York NY 2013.
- Qualitätsorientierung (Memento vom 30. Januar 2012 im Internet Archive) (PDF; 140 kB)
- Komplexität und Qualität (PDF; 69 kB)
- Hoyningen-Huene: Logik. 1998, S. 255.
- Hügli, Lübcke: Philosophielexikon. 1991, ISBN 3-634-22405-3.
- Godehard Link, Karl-Georg Niebergall: Logik: Von Epimenides zu Gödel. In: E. Fischer, W. Vossenkuhl: Die Fragen der Philosophie. Beck, München 2003, S. 107 (118)
- Wilhelm K. Essler: Einführung in die Logik (= Kröners Taschenausgabe. Band 381). 2., erweiterte Auflage. Kröner, Stuttgart 1969, DNB 456577998, S. 244.
- Rudolf Carnap: Einführung in die symbolische Logik. 3. Auflage. Springer, Wien / New York 1968, S. 174
- Nach Helmut Glück (Hrsg.): Metzler Lexikon Sprache. 4. Auflage. Metzler, Stuttgart/Weimar 2010: Modell.
- Ähnlich in anderer Formulierung Rainer Stuhlmann-Laeisz: Rainer Stuhlmann-Laeisz: Philosophische Logik. mentis, Paderborn, 2002, S. 21
- „Ein Modell U zu einer Sprache MAL ist ein Gebilde (K, i, R, V) aus vier Bestandteilen:
- (i) K ist eine nicht-leere Klasse oder Menge von Objekten,
- (ii) i ist eines der Objekte in K: i ist Element von K,
- (iii) R ist eine zweistellige Relation auf K: R ist Teilmenge in K × K,
- (iv) V ist eine Zuordnung, die jeder atomaren Aussage von MAL im Hinblick auf das Objekt aus K einen Wahrheitswert zuweist; V: At × K → (W,F) (in dieser Notation steht die Bezeichnung ‚At‘ für die Klasse der atomaren Aussagen (Aussagebuchstaben) von MAL).“
- E. T. Hall: Beyond Culture. Random House 1976, S. 13.
- N. Kühne, S. 53 ff.
- Reinhard Tausch, Anne-Marie Tausch, Göttingen 1971, S. 49–73.
- Siehe Tausch/Tausch, Göttingen 1971, S. 49–73.
- Hans Albert: Modell-Platonismus. Der neoklassische Stil des ökonomischen Denkens in kritischer Beleuchtung. In: Ernst Topitsch, (Hrsg.): Logik der Sozialwissenschaften. Kiepenheuer & Witsch, Köln/Berlin 1965, S. 406–434; zitiert nach: Friedrich Karrenberg, Hans Albert (Hrsg.): Sozialwissenschaft und Gesellschaftsgestaltung. Festschrift für Gerhard Weisser. Duncker & Humblot, Berlin 1963, S. 45–76.
- Hans Albert: Der logische Charakter der theoretischen Nationalökonomie. In: Jahrbücher für Nationalökonomie und Statistik, 171, 1959, S. 1 ff.
- Hans Reichenbach: Der Aufstieg der wissenschaftlichen Philosophie. Friedrich Vieweg & Sohn, Braunschweig 1968, S. 42.
- Siehe dazu Hans Albert: Marktsoziologie und Entscheidungslogik. (Mohr Siebeck) Tübingen 1998, insb. Kapitel IV. Und sein Vortrag Die Idee rationaler Praxis und die ökonomische Tradition (PDF)