Gerichteter Graph

Ein gerichteter Graph oder Digraph (von englisch directed graph) besteht aus

einer Menge $V$ von Knoten (englisch vertex/vertices, oft auch Ecken genannt) und
einer Menge geordneter Knotenpaare $E\subseteq V\times V$ von Kanten.[1]

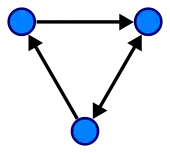
Ein gerichteter Graph mit 3 Knoten und 4 gerichteten Kanten (Doppelpfeil entspricht zwei gegenläufigen Pfeilen)

Die Kanten $(v,w)\in E$ eines gerichteten Graphen sind gerichtete Kanten (englisch directed edge/edges, manchmal auch Bögen). Diese werden häufig als Pfeile dargestellt und können nur in einer Richtung durchlaufen werden. Im Gegensatz dazu sind die Kanten eines ungerichteten Graphen ungeordnete Knotenpaare $\{v,w\}$ . Gerichtete Graphen werden dazu benutzt, Objekte und die dazwischenliegenden Verbindungen, beispielsweise von endlichen Automaten, darzustellen.

Grundbegriffe

Ein gerichteter Graph ohne Mehrfachkanten und Schleifen wird einfacher Digraph[2] (auch schlichter Digraph) genannt.

Man sagt, dass eine gerichtete Kante $e=(x,y)$ von $x$ nach $y$ geht. Dabei ist $x$ der Fuß (oder Startknoten) und $y$ der Kopf (oder Endknoten) von $e$ . Weiterhin gilt $y$ als der direkte Nachfolger von $x$ und $x$ als der direkte Vorgänger von $y$ . Falls in einem Graphen von $x$ nach $y$ ein Pfad führt, gilt $y$ als ein Nachfolger von $x$ und $x$ als ein Vorgänger von $y$ . Die Kante $(y,x)$ heißt umgedrehte oder invertierte Kante von $(x,y)$ .

Ein gerichteter Graph $G$ heißt symmetrisch, falls $G$ zu jeder Kante auch die entsprechende invertierte Kante enthält. Ein ungerichteter Graph lässt sich einfach in einen symmetrischen gerichteten Graphen umwandeln, indem man jede Kante $\{x,y\}$ durch die zwei gerichteten Kanten $(x,y)$ und $(y,x)$ ersetzt.

Um eine Orientierung eines einfachen ungerichteten Graphen zu erhalten, muss jeder Kante eine Richtung zugewiesen werden. Jeder auf diese Art konstruierte gerichtete Graph wird orientierter Graph genannt. Ein einfach gerichteter Graph darf, im Gegensatz zum orientierten Graphen, zwischen zwei Knoten Kanten in beide Richtungen enthalten.[1][3][4]

Ein gewichteter Digraph ist ein Digraph, dessen Kanten Gewichte zugeordnet werden, wodurch man einen kantengewichteten Graphen erhält. Ein Digraph mit gewichteten Kanten wird in der Graphentheorie als Netzwerk bezeichnet.[5]

Die Adjazenzmatrix eines Digraphen (mit Schleifen und Mehrfachkanten) ist eine ganzzahlige Matrix, deren Zeilen und Spalten den Knoten des Digraphen entsprechen. Ein Eintrag $a_{ij}$ außerhalb der Hauptdiagonalen gibt die Anzahl der Kanten vom Knoten $i$ zum Knoten $j$ an, und der Eintrag der Hauptdiagonalen $a_{ii}$ entspricht der Anzahl der Schleifen im Knoten $i$ . Die Adjazenzmatrix eines Digraphen ist bis auf Vertauschung von Zeilen und Spalten eindeutig.

Ein Digraph lässt sich auch durch eine Inzidenzmatrix repräsentieren.

Zusammenhängende gerichtete Graphen

Ein gerichteter Graph $G$ heißt schwach zusammenhängend (oder nur zusammenhängend),[6] falls der unterliegende Graph von $G$ , den man mittels Ersetzung aller gerichteter Kanten durch ungerichtete erhält, ein zusammenhängender Graph ist. Ein gerichteter Graph heißt stark zusammenhängend oder stark, wenn je zwei seiner Knoten gegenseitig erreichbar sind. Ein maximaler stark zusammenhängender Untergraph von $G$ ist eine starke Komponente.

Eingangs- und Ausgangsgrad

Digraph mit Knotenbeschriftung (Eingangs- und Ausgangsgrad).

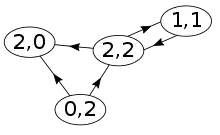
Die Anzahl der direkten Vorgänger eines Knotens wird Eingangsgrad (auch Innengrad) und die Anzahl der direkten Nachfolger Ausgangsgrad (oder Außengrad) genannt.

Der Eingangsgrad eines Knotens $v$ in einem Graphen $G$ wird mit $d_{G}^{-}(v)$ und der Außengrad mit $d_{G}^{+}(v)$ bezeichnet. Ein Knoten mit $d_{G}^{-}(v)=0$ wird Quelle und ein Knoten mit $d_{G}^{+}(v)=0$ wird Senke genannt. Eine Senke heißt universelle Senke, falls sie eingehende Kanten von jedem anderen Knoten hat, falls also ihr Eingangsgrad gleich $|V|-1$ ist.

Für gerichtete Graphen ist die Summe aller Eingangsgrade gleich der Summe aller Ausgangsgrade, und beide gleich der Summe der gerichteten Kanten:

\sum _{v\in V}d_{G}^{+}(v)=\sum _{v\in V}d_{G}^{-}(v)=|E|\,.

Falls für alle Knoten $v\in V$ die Gleichung $d_{G}^{+}(v)=d_{G}^{-}(v)$ gilt, wird der Graph balancierter Digraph genannt.[7][8]

Darstellung von gerichteten Graphen

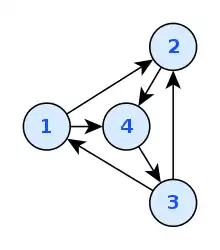
Der im Beispiel behandelte gerichtete Graph

Außer der naiven Darstellung eines gerichteten Graphen durch Angabe der Knoten- und Kantenmenge gibt es noch weitere Darstellungsmöglichkeiten, das sogenannte Kanten bzw. Knotenfeld.

Kantenfeld

Ein Kantenfeld ist eine Darstellungsart für gerichtete Graphen nach folgendem Schema:

|V|,|E|,E_{1},\ldots ,E_{|E|}

,

wobei $|V|$ die Anzahl der Knoten, $|E|$ die Anzahl der Kanten und $E_{1},\ldots ,E_{|E|}$ die Kanten mit $E_{i}=(v,w)\in E$ sind.

Knotenfeld

Ein Knotenfeld ist eine Darstellungsart für gerichtete Graphen mit folgendem Aufbau:

|V|,|E|,{\text{ag}}(V_{1}),{\text{Ziel}}_{1},\ldots ,{\text{Ziel}}_{{\text{ag}}(V_{1})},\ldots ,{\text{ag}}(V_{|V|}),{\text{Ziel}}_{1},\ldots ,{\text{Ziel}}_{{\text{ag}}(V_{|V|})}

,

wobei $|V|$ die Anzahl der Knoten, $|E|$ die Anzahl der Kanten und $ag(V)$ der Ausgangsgrad des Knotens $V$ sind.

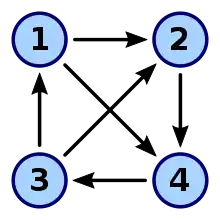
Beispiel

Betrachtet man als Beispiel den rechts stehenden gerichteten Graph, so ist das Kantenfeld $4,6,(1,2),(1,4),(2,4),(3,1),(3,2),(4,3)$ und das Knotenfeld $4,6,\mathbf {2} ,2,4,\mathbf {1} ,4,\mathbf {2} ,1,2,\mathbf {1} ,3$ . Die fett gedruckten Zahlen geben den Ausgangsgrad an.

Klassen von gerichteten Graphen

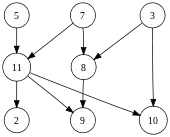
Einfach gerichteter azyklischer Graph

Turniergraph mit 4 Knoten

Symmetrisch gerichtete Graphen sind gerichtete Graphen, bei denen alle Kanten bidirektional sind, d. h. für jede Kante, die zum Graphen gehört, gehört auch die entsprechende umgekehrte Kante dazu.

Einfache gerichtete Graphen sind gerichtete Graphen ohne Schleifen und ohne Mehrfachkante.

Vollständige gerichtete Graphen sind einfache gerichtete Graphen, bei denen jedes Knotenpaar durch ein symmetrisches Paar gerichteter Kanten verbunden ist. Dies entspricht einem ungerichteten vollständigen Graphen, dessen Kanten durch Paare von gerichteten Kanten ersetzt werden. Daraus folgt, dass ein vollständiger gerichteter Graph symmetrisch ist.

Orientierte Graphen sind gerichtete Graphen ohne bidirektionale Kanten. Daraus folgt, dass ein gerichteter Graph genau dann ein orientierter Graph ist, wenn er keinen 2-Zyklus hat.

Turniergraphen sind orientierte Graphen, die durch Auswahl einer Richtung für jede Kante in ungerichteten vollständigen Graphen erhalten werden.

Ein gerichteter azyklischer Graph oder azyklischer Digraph ist ein gerichteter Graph, der keinen gerichteten Kreis enthält. Spezialfälle gerichteter azyklischer Graphen sind Mehrfachbäume (je zwei gerichtete Pfade des Graphen, die vom selben Startknoten ausgehen, dürfen sich nicht im selben Endknoten treffen), orientierte Bäume oder Polybäume (Orientierung eines ungerichteten azyklischen Graphen) und Wurzelbäume (orientierte Bäume, bei denen alle Kanten des unterliegenden ungerichteten Baumes vom Wurzelknoten wegführen).

Gewichtete gerichtete Graphen oder gerichtete Netzwerke sind einfache gerichtete Graphen mit Gewichten, die ihren Kanten zugewiesen sind, ähnlich wie gewichtete Graphen, die auch als ungerichtete Netzwerke oder gewichtete Netzwerke bezeichnet werden.

Flussnetzwerke sind gewichtete gerichtete Graphen mit zwei speziellen Knoten, der Quelle und der Senke.

Kontrollflussgraphen sind gerichtete Graphen, die in der Informatik zur Darstellung der Pfade verwendet werden, die während der Ausführung eines Computerprogramms durchlaufen werden können.

Signalflussgraphen sind gewichtete gerichtete Graphen, in denen Knoten Systemvariablen darstellen und Kanten funktionale Verbindungen zwischen Knotenpaaren darstellen.

Zustandsübergangsdiagramme sind gerichtete Multigraphen, die endliche Automaten darstellen.

Kommutative Diagramme sind gerichtete Graphen, die in der Kategorientheorie verwendet werden, wobei die Knoten mathematische Objekte und die Kanten mathematische Funktionen darstellen, mit der Eigenschaft, dass alle gerichteten Pfade mit demselben Start- und Endknoten durch Komposition zum gleichen Ergebnis führen.

Kombinatorik

Die Anzahl der einfachen gerichteten Graphen mit $n$ Knoten steigt rasant mit der Anzahl der Knoten und ist gleich $4^{\tfrac {n\cdot (n-1)}{2}}$ . Sie steigt also exponentiell zur Anzahl ${\tfrac {n\cdot (n-1)}{2}}$ der Kanten des vollständigen Graphen $K_{n}$ . Wenn die Knoten nicht nummeriert sind, isomorphe Graphen also nicht mitgezählt werden, ist diese Anzahl etwa proportional zu ${\tfrac {1}{n!}}\cdot 4^{\tfrac {n\cdot (n-1)}{2}}$ , weil für die meisten Isomorphieklassen alle $n!$ Graphen, die sich durch Permutation der nummerierten Knoten ergeben, verschieden sind. Die folgende Tabelle zeigt die mit Hilfe eines Computers bestimmten Anzahlen für $n\leq 8$ :[9][10][11]

Anzahl der gerichteten Graphen ohne nummerierte Knoten
n	alle	zusammenhängend	stark zusammenhängend
1	1	1	1
2	3	2	1
3	16	13	5
4	218	199	83
5	9608	9364	5048
6	1540944	1530843	1047008
7	882033440	880471142	705422362
8	1793359192848	1792473955306	1580348371788

Programmierung

Das folgende Beispiel in der Programmiersprache C++ zeigt die Implementierung eines gerichteten Graphen mit Adjazenzlisten. Der gerichtete Graph wird als Klasse DirectedGraph deklariert. Bei der Ausführung des Programms wird die Methode main verwendet.[12]

#include <iostream>

using namespace std;

// Deklariert den Datentyp für die Knoten des Graphen
struct Node
{
    int index;
    string value;
    Node* next;
};

// Deklariert den Datentyp für die Kanten des Graphen
struct Edge
{
    int startIndex;
    int endIndex;
};

// Deklariert die Klasse für den gerichteten Graphen
class DirectedGraph
{
public:
    Node** headNode;

    // Diese Methode fügt einen neuen Knoten in die Adjazenzliste des Graphen ein und gibt ihn als Rückgabewert zurück
    Node* insertNewNode(int index, string value, Node* node)
    {
        Node* newNode = new Node; // Erzeugt einen neuen Knoten vom Typ Node
        newNode->index = index; // Setzt den Index
        newNode->value = value; // Setzt den Wert
        newNode->next = node; // Setzt einen Zeiger auf den Nachfolger
        return newNode;
    }

    // Konstruktor, der den gerichteten Graphen mit den gegebenen Knoten und Kanten erzeugt
    DirectedGraph(Node nodes[], Edge edges[], int numberOfEdges, int numberOfNodes)
    {
        headNode = new Node*[numberOfNodes](); // Initialisiert ein Array von Zeigern für die Knoten
        for (int i = 0; i < numberOfEdges; i++) // for-Schleife, die alle Kanten des Graphen durchläuft
        {
            int startIndex = edges[i].startIndex; // Index des Startknotens der Kante
            int endIndex = edges[i].endIndex; // Index des Endknotens der Kante
            string value = nodes[endIndex].value; // Wert des Endknotens der Kante
            Node* newNode = insertNewNode(endIndex, value, headNode[startIndex]); // Aufruf der Methode insertNewNode, um einen neuen Knoten einzufügen
            headNode[startIndex] = newNode; // Setzt den Zeiger auf den neuen Knoten
        }
    }
};

// Gibt alle benachbarten Knoten von node auf der Konsole aus
void writeAdjacencyList(Node* node, int i)
{
    cout << "Knoten " << (i + 1) << ": ";
    while (node != nullptr)
    {
        cout << "(" << node->index << ", " << node->value << ") ";
        node = node->next;
    }
    cout << endl;
}

// Hauptmethode, die das Programm ausführt
int main()
{
    // Deklariert und initialisiert Arrays für die Knoten und Kanten
    Node nodes[] = { {0,"A"},{1,"B"},{2,"C"},{3,"D"},{4,"E"} };
    Edge edges[] = { {0,1},{0,2},{1,4},{2,3},{3,1},{4,3} };
    int numberOfNodes = sizeof(nodes); // Ermittelt die Anzahl der Knoten
    int numberOfEdges = sizeof(edges) / sizeof(edges[0]); // Ermittelt die Anzahl der Kanten
    DirectedGraph directedGraph(nodes, edges, numberOfEdges, numberOfNodes); // Erzeugt den gerichteten Graphen mit den gegebenen Knoten und Kanten
    for (int i = 0; i < numberOfNodes; i++) // for-Schleife, die alle Knoten des Graphen durchläuft
    {
        Node* headNode = directedGraph.headNode[i];
        writeAdjacencyList(headNode, i); // Gibt die Adjazenzliste für den Knoten headNode aus
    }
}

Siehe auch

Kautz-Graph

Literatur

Jørgen Bang-Jensen, Gregory Gutin: Digraphs: Theory, Algorithms and Applications. Springer, 2000, ISBN 1-85233-268-9 (rhul.ac.uk).
John Adrian Bondy, U. S. R. Murty: Graph Theory with Applications. North-Holland, 1976, ISBN 0-444-19451-7.
Reinhard Diestel: Graph Theory. 3. Auflage. Springer, 2005, ISBN 3-540-26182-6.
Frank Harary, Robert Z. Norman, Dorwin Cartwright: Structural Models: An Introduction to the Theory of Directed Graphs. Wiley, New York 1965.

Einzelnachweise

Reinhard Diestel: Graphentheorie. 4. Auflage. Springer, Berlin u. a. 2010, ISBN 978-3-642-14911-5, S. 28–30 (englisch, 4. elektronische Ausgabe 2010 – Erstausgabe: 1996).
Volker Turau: Algorithmische Graphentheorie. 3. Auflage. Oldenbourg Wissenschaftsverlag, München 2009, ISBN 978-3-486-59057-9, S. 20–24.
Eric W. Weisstein: Oriented Graph. In: MathWorld (englisch).
Eric W. Weisstein: Graph Orientation. In: MathWorld (englisch).
Reinhard Diestel: Graphentheorie. 4. Auflage. Springer, Berlin u. a. 2010, ISBN 978-3-642-14911-5, S. 145–168 (englisch, 4. elektronische Ausgabe 2010 – Erstausgabe: 1996).
Bang-Jensen, Gutin: Digraphs: Theory, Algorithms and Applications, 2. Auflage, 2009, S. 20.
Bhavanari Satyanarayana, Kuncham Syam Prasad: Discrete Mathematics and Graph Theory. PHI Learning Pvt. Ltd., 2009, ISBN 978-81-203-3842-5, S. 460.
Richard A. Brualdi: Combinatorial matrix classes. In: Encyclopedia of mathematics and its applications. Band 108. Cambridge University Press, 2006, ISBN 978-0-521-86565-4, S. 51.
Folge A000088 in OEIS
Folge A003085 in OEIS
Folge A035512 in OEIS
Software Testing Help: Graph Implementation In C++ Using Adjacency List

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Diestel2010-1] Reinhard Diestel: Graphentheorie. 4. Auflage. Springer, Berlin u. a. 2010, ISBN 978-3-642-14911-5, S. 28–30 (englisch, 4. elektronische Ausgabe 2010 – Erstausgabe: 1996).

[2] Volker Turau: Algorithmische Graphentheorie. 3. Auflage. Oldenbourg Wissenschaftsverlag, München 2009, ISBN 978-3-486-59057-9, S. 20–24.

[3] Eric W. Weisstein: Oriented Graph. In: MathWorld (englisch).

[4] Eric W. Weisstein: Graph Orientation. In: MathWorld (englisch).

[5] Reinhard Diestel: Graphentheorie. 4. Auflage. Springer, Berlin u. a. 2010, ISBN 978-3-642-14911-5, S. 145–168 (englisch, 4. elektronische Ausgabe 2010 – Erstausgabe: 1996).

[6] Bang-Jensen, Gutin: Digraphs: Theory, Algorithms and Applications, 2. Auflage, 2009, S. 20.

[7] Bhavanari Satyanarayana, Kuncham Syam Prasad: Discrete Mathematics and Graph Theory. PHI Learning Pvt. Ltd., 2009, ISBN 978-81-203-3842-5, S. 460.

[8] Richard A. Brualdi: Combinatorial matrix classes. In: Encyclopedia of mathematics and its applications. Band 108. Cambridge University Press, 2006, ISBN 978-0-521-86565-4, S. 51.

[9] Folge A000088 in OEIS

[10] Folge A003085 in OEIS

[11] Folge A035512 in OEIS

[12] Software Testing Help: Graph Implementation In C++ Using Adjacency List