Harmonischer Oszillator

Ein harmonischer Oszillator ist ein schwingungsfähiges System, das sich durch eine lineare Rückstellgröße auszeichnet. Für ein mechanisches System bedeutet dies, dass es eine Kraft gibt, die einer zunehmenden Auslenkung mit proportional anwachsender Stärke entgegenwirkt. Nach einem Anstoß von außen schwingt ein harmonischer Oszillator sinusförmig (= harmonisch) um seine Ruhelage, wobei die Schwingungsdauer unabhängig von der Größe der Auslenkung ist. Beispiele für harmonische Oszillatoren sind Federpendel, elektrische Schwingkreise und Stimmgabeln.

Der harmonische Oszillator ist ein wichtiges Modellsystem der Physik. Er ist durch nur zwei Parameter vollständig beschrieben, die Eigenfrequenz und die Dämpfung. Viele komplexere Systeme verhalten sich bei kleinen Auslenkungen näherungsweise wie harmonische Oszillatoren, z. B. das Fadenpendel. Der harmonische Oszillator in der Quantenmechanik ist eines der wenigen quantenmechanischen Systeme, das sich ohne Näherungen berechnen lässt.

Die Bezeichnung harmonischer Oszillator wird auch für gedämpfte harmonische Oszillatoren verwendet, auch wenn diese streng genommen keine harmonische Schwingung vollziehen, sondern eine gedämpfte Schwingung.

Differentialgleichung des harmonischen Oszillators

Mathematisch lässt sich jeder freie harmonische Oszillator durch die folgende Differentialgleichung beschreiben. Ausnahmen sind Oszillatoren in der Quantenmechanik und verwandten Theorien, bei denen Unschärferelationen berücksichtigt werden müssen.

{\ddot {x}}+\omega _{0}^{2}\,x=0

Dabei sind $x(t)$ die Auslenkung des Systems und $\omega _{0}$ die Resonanzfrequenz. Es handelt sich um eine gewöhnliche, lineare, homogene Differentialgleichung zweiter Ordnung, die sich daher einfach analytisch lösen lässt. Die Lösung $x(t)$ einer solchen Gleichung ist eine sinusförmige Funktion.

Potential des harmonischen Oszillators

Das Potential V eines eindimensionalen harmonischen Oszillators

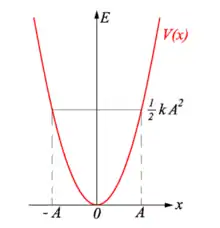
Der ungedämpfte harmonische Oszillator ist ein konservatives System. Dies bedeutet, dass die Energie der Schwingung erhalten bleibt. Es existiert daher für jedes Oszillator-Kraftfeld ein Potential.

Eindimensionaler Oszillator

Die graphische Darstellung des Potentials $V$ eines harmonischen Oszillators ist eine Parabel. Man nennt es auch harmonisches Potential.

V(x)={\frac {1}{2}}kx^{2}

mit der Richtgröße

k>0

In der Mechanik ist die Kraft $F$ auf ein Teilchen in einem solchen Potential durch die negative Ableitung des Potentials gegeben.

F=-{\frac {\mathrm {d} V}{\mathrm {d} x}}=-kx

Mehrdimensionaler Oszillator

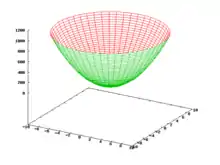
Das Potential eines zweidimensionalen isotropen harmonischen Oszillators

Dieses Konzept lässt sich auf mehrere Dimensionen übertragen. Das Potential hat hier die Form eines elliptischen Paraboloids. In n Dimensionen lässt es sich bei geeigneter Wahl der Koordinaten wie folgt schreiben:

V(x_{1},\dotsc ,x_{n})={\frac {1}{2}}\sum _{i=1}^{n}k_{i}\,x_{i}^{2}

In der Mechanik ist die Kraft auf ein Teilchen in einem solchen Potential durch den negativen Gradienten des Potentials gegeben.

Weil in den einzelnen Summanden keine Mischterme zwischen unterschiedlichen Richtungen vorkommen, lässt sich das Problem eines n-dimensionalen harmonischen Oszillators auf n eindimensionale Oszillatoren zurückführen. In der Quantenmechanik wird eine solche Eigenschaft Separabilität genannt. Es lässt sich folgern, dass bei einem harmonischen Oszillator nicht nur die Gesamtenergie, sondern auch die Energien für die Komponenten jeder einzelnen Richtung Erhaltungsgrößen sind.

Hängt der Wert des Potentials nur von der Entfernung zum Nullpunkt, nicht aber von der Richtung ab, so nennt man den Oszillator isotrop, andernfalls anisotrop. Bei einem isotropen Oszillator haben also alle Konstanten den gleichen Wert:

k_{i}=c>0~~~~~~~~\forall i=1,\ldots ,n

und Schwingungen in jeder Richtung sind harmonisch und haben dieselbe Frequenz.

Bei einem anisotropen Oszillator sind die Schwingungen in jeweils einer einzigen Koordinate $x_{i}$ harmonisch und haben eine von $k_{i}$ abhängige Frequenz (Normalschwingungen). Sind mehrere Normalschwingungen mit unterschiedlichen $k_{i}$ angeregt, ergeben sich kompliziertere, möglicherweise auch nichtperiodische Bewegungen.

Minimum des Potentials

Das Minimum dieses Potentials ist ein stabiler Fixpunkt des Systems. In der Mechanik nennt man diesen Punkt auch Ruhelage und die Kraft, die das Teilchen erfährt, Rückstell- oder Rückholkraft. Insbesondere erfährt ein in der Ruhelage liegendes Teilchen keinerlei Kraft, woraus sich auch der Name „Ruhelage“ ableitet. Die Namensgebung ist allerdings in dieser Hinsicht etwas irreführend: Zwar wirkt auf ein Teilchen in der Ruhelage keine Kraft, das Teilchen muss sich dort allerdings keinesfalls in Ruhe befinden. Im Allgemeinen nimmt es dort sogar seine Maximalgeschwindigkeit an.

Bedeutung in der Physik

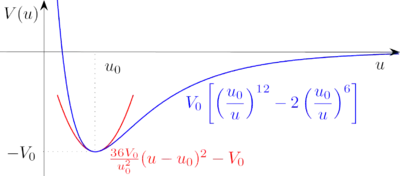
Quadratische Approximation des Lennard-Jones-(12,6)-Potentials. Der Variablen x entspricht die Entfernung u.

Ein idealer harmonischer Oszillator, bei dem die Rückstellkraft für beliebig große Auslenkungen linear mit der Auslenkung ansteigt, existiert in der Natur nicht. Dennoch ist das Konzept für die Physik von fundamentaler Bedeutung, da es durch viele Systeme sehr gut angenähert wird, vor allem, wenn nur kleine Auslenkungen aus der Ruhelage betrachtet werden. Beschränkt man sich darauf, so können Potentiale, die ein lokales Minimum besitzen, in guter Näherung durch ein harmonisches Potential ersetzt und das gesamte Problem als harmonischer Oszillator beschrieben werden. Der Vorteil einer solchen harmonischen Näherung besteht darin, dass das Problem mit Standardmethoden der theoretischen Physik handhabbar wird und einfach zu interpretierende, analytische Lösungen liefert. In der nebenstehenden Abbildung wurde dies für ein Lennard-Jones-(12,6)-Potential (blaue Kurve) durchgeführt. Das Ergebnis (rote Kurve) ist wie ersichtlich nur für kleine Abstände vom Minimum eine brauchbare Näherung.

Ihre mathematische Begründung findet die harmonische Näherung in der Tatsache, dass die Potentiale in einer Taylorreihe entwickelt werden können. Ist ein Potential $V$ gegeben und ist dieses hinreichend oft differenzierbar, so gilt nach dem Satz von Taylor:

V(x)=V(x_{0})+{\frac {\partial V}{\partial x}}(x_{0})(x-x_{0})+{\frac {1}{2}}{\frac {\partial ^{2}V}{\partial x^{2}}}(x_{0})(x-x_{0})^{2}+R(x-x_{0})

wobei $R(x-x_{0})$ , das sogenannte Restglied, nur Terme ab dritter Ordnung enthält. Für kleine Abstände $x-x_{0}$ ist es daher vernachlässigbar. Als Entwicklungspunkt $x_{0}$ wählen wir ein Minimum des Potentials, sodass gilt ${\tfrac {\partial V}{\partial x}}(x_{0})=0$ . Somit entfällt auch der Term erster Ordnung. Zur besseren mathematischen Handhabung kann durch eine geeignete Koordinatentransformation der Scheitelpunkt in den Koordinatenursprung gelegt werden, damit gilt: $x_{0}=0$ . Weiterhin ist es stets möglich $V(x_{0})=0$ zu setzen. Man erhält dann näherungsweise das harmonische Potential:

V(x)={\frac {1}{2}}kx^{2}

mit

k={\frac {\partial ^{2}V}{\partial x^{2}}}(x_{0})

Das heißt, bei genügend kleiner Auslenkung verhält sich der Oszillator harmonisch. Beispiele für Oszillatoren, die bereits bei mittleren Amplituden anharmonisch werden, sind das Fadenpendel und die transversal schwingende Saite.

Ein approximatives Lösungsverfahren, bei dem ein kompliziertes Problem zunächst auf ein analytisch lösbares zurückgeführt wird, um dann der Lösung zuvor ignorierte Einflüsse in Form von Störungen wieder hinzuzufügen, wird als Störungstheorie bezeichnet.

Der harmonische Oszillator der klassischen Mechanik

Eindimensionaler ungedämpfter Oszillator

Ein mechanischer Oszillator besteht aus einem Körper der Masse und aus einer Kraft, die diesen zurücktreibt, wenn man ihn aus seiner Ruhelage auslenkt. Damit ein Oszillator ein harmonischer ist, muss die rücktreibende Kraft proportional zu dieser Auslenkung, also der Entfernung des Körpers von seiner Ruhelage, sein. In der Praxis wird eine solche Kraft meist durch Federn, wie bei einem Federpendel realisiert, oder durch die Gewichtskraft des Körpers, wie es beispielsweise bei einem Wasserpendel der Fall ist.

Beschreibung des Schwingvorgangs

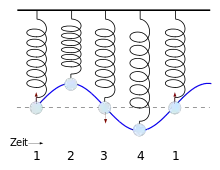
Darstellung der Schwingung eines harmonischen Oszillators am Beispiel eines Federpendels. Die Ruhelage des Oszillators ist mit einer gestrichelten Linie markiert. Die Geschwindigkeit ist jeweils als roter Pfeil gekennzeichnet

Ein harmonischer Oszillator wird aus seiner Ruhelage bewegt. Je weiter man ihn entfernt, desto größer wird die Kraft, die versucht ihn zurückzubewegen. Durch das Auslenken wird dem Oszillator potentielle Energie hinzugefügt. Potentiell bedeutet, dass die Energie verwendet wird, um beispielsweise eine Feder zu spannen und somit diese Energie in der Position des Oszillators gespeichert ist.

Wird der Oszillator dann freigelassen, so wird er auf Grund der Zugkraft der Feder beschleunigt. Er bewegt sich daher mit zunehmender Geschwindigkeit zur Ruhelage zurück. Wenn er dort angelangt ist, so hat der Oszillator seine maximale Geschwindigkeit erreicht. Die Feder ist entspannt und es wirkt keine Kraft mehr auf den Oszillator. Die potentielle Energie, die ihm zugeführt wurde, ist nun vollständig in kinetische Energie umgewandelt worden. Dies bedeutet, sie ist jetzt nicht mehr in der Position, sondern in der Geschwindigkeit des Oszillators gespeichert.

Aufgrund der Trägheit bewegt sich der Oszillator jedoch weiter. Dies führt dazu, dass die Feder, diesmal in anderer Richtung, wieder gespannt wird. Für das Spannen dieser Feder muss der Oszillator seine kinetische Energie aufwenden, um sich gegen die Kraft der Feder bewegen zu können. Er wird dadurch langsamer, bis er den Punkt erreicht, an dem er sich nicht mehr bewegt und die gesamte Energie wieder in Form von potentieller Energie vorliegt. Der Bewegungsablauf beginnt dann wieder von vorne.

Zeitpunkt [Anm. 1]	Auslenkung $x$	potentielle Energie ${\frac {k}{2}}x^{2}$	Geschwindigkeit ${\dot {x}}$	kinetische Energie ${\frac {m}{2}}{\dot {x}}^{2}$
1	$0$	$0$	${\sqrt {2E/m}}$	$E$
2	${\sqrt {2E/k}}$	$E$	$0$	$0$
3	$0$	$0$	$-{\sqrt {2E/m}}$	$E$
4	$-{\sqrt {2E/k}}$	$E$	$0$	$0$
unveränderlich: Gesamtenergie $E$ , Masse $m$ und Federkonstante $k$

Herleitung der Schwingungsgleichung

Illustration der physikalischen Größen bei einem Federpendel. Die Kraft ist als grüner Pfeil eingezeichnet

Wir nehmen wie oben als Beispiel ein Federpendel. Die Masse des Körpers ist $m$ . Die Ruhelage nehmen wir als Nullpunkt und bezeichnen die Auslenkung mit $x$ . Die Kraft $F$ , die auf den Körper wirkt, wird durch das Hookesche Gesetz beschrieben:

F=-kx

Die Konstante $k$ ist eine Federkonstante, die sich nach der Stärke der rücktreibenden Kraft bei einer festen Auslenkung richtet. Außerdem ist bekannt, dass die Beschleunigung eines Körpers proportional zu der auf ihn einwirkenden Kraft ist. Die Beschleunigung lässt sich als zweite Ableitung des Ortes $x$ nach der Zeit schreiben. Eine zeitliche Ableitung wird in der Physik häufig als Punkt über der Variablen gekennzeichnet:

F=m{\ddot {x}}

Setzt man nun diese beiden Ausdrücke für die Kraft $F$ gleich, erhält man eine Differenzialgleichung:

m{\ddot {x}}=-kx

Um die folgenden Rechnungen zu vereinfachen, substituiert man $\omega _{0}^{2}={\frac {k}{m}}$ und schreibt die Gleichung um zu:

{\ddot {x}}+\omega _{0}^{2}x=0

Diese Gleichung lässt sich beispielsweise mittels eines Exponentialansatzes lösen. Als Ergebnis erhält man eine sinusförmige Funktion, auch harmonische Schwingung genannt:

x(t)=u\,\sin(\omega _{0}t+\varphi )

.

Die Lösung enthält zwei Konstanten, die Amplitude $u$ und den Phasenverschiebungswinkel $\varphi$ . Man erhält sie entsprechend den Anfangsbedingungen. Die Amplitude steht für die maximale Auslenkung des Oszillators und damit die Energie der Schwingung. Der Phasenverschiebungswinkel bestimmt die Position und gleichzeitig damit die Geschwindigkeit, welche der Körper zum Zeitpunkt $t=0$ hat.

Die Sinusfunktion ist eine periodische Funktion, da ihre Werte sich in regelmäßigen Abständen wiederholen ( $\sin(x)=\sin(x+2\pi )$ ). Daher führt der Oszillator eine periodische Bewegung aus. $\omega _{0}$ bezeichnet die Eigenkreisfrequenz und Resonanzfrequenz des Oszillators. Sie bestimmt die Frequenz $f={\frac {\omega _{0}}{2\pi }}$ , mit der der Oszillator schwingt. Bei einem harmonischen Oszillator ist diese Frequenz unabhängig von der Schwingungsamplitude.

Energie

Beim freien ungedämpften Oszillator bleibt die Energie erhalten, weil es sich um ein abgeschlossenes System handelt und nur konservative Kräfte auftreten. In der Gleichgewichtslage verschwindet die potenzielle Energie. Deshalb ist die Gesamtenergie gleich der maximalen kinetischen Energie:

E_{\text{gesamt}}={\hat {E}}_{\text{kin}}={\frac {1}{2}}m{\hat {v}}^{2}={\frac {1}{2}}m\omega ^{2}{\hat {x}}^{2}

Zu demselben Ergebnis kommt man, wenn man die Gesamtenergie über den Maximalwert der potenziellen Energie berechnet:

E_{\text{gesamt}}={\hat {E}}_{\text{pot}}={\frac {1}{2}}k{\hat {x}}^{2}={\frac {1}{2}}m{\sqrt {\frac {k}{m}}}^{2}{\hat {x}}^{2}={\frac {1}{2}}m\omega ^{2}{\hat {x}}^{2}

.

${\hat {x}}$ steht hier jeweils für den Maximalwert der Auslenkung, also für die Amplitude. Wird mit komplexen Zahlen gerechnet, so tritt an die Stelle von ${\hat {x}}^{2}$ das Betragsquadrat der gegebenenfalls komplexwertigen Amplitude.

Eindimensionaler gedämpfter Oszillator

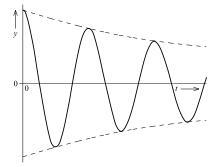
schwach, linear gedämpfte Oszillation eines harmonischen Oszillators

Eine mechanische Schwingung ist im Allgemeinen nicht reibungsfrei. Das heißt, die Schwingung verliert durch Reibung Energie und daher nimmt ihre Amplitude ab. Man spricht von einer Dämpfung der Schwingung, wodurch diese im Allgemeinen nicht mehr harmonisch ist. Ein solches System ist nicht mehr konservativ, sondern dissipativ. In der Differentialgleichung tritt dann zur beschleunigenden Kraft F eine Reibungskraft F_R hinzu.

m{\ddot {x}}(t)=-kx(t)+F_{\mathrm {R} }

Das Vorzeichen der Kraft ist der Geschwindigkeit entgegengesetzt. Der genaue Ausdruck für F_R hängt von der Art der Reibung ab. So kann der Betrag von F konstant sein, oder beispielsweise eine lineare oder quadratische Abhängigkeit von der Geschwindigkeit besitzen.

Im Falle von Gleitreibung ist der Betrag von F_R konstant:

F_{\mathrm {R} }=-d\operatorname {sgn} \left({\dot {x}}(t)\right)

Ein Beispiel für eine lineare Abhängigkeit ist die Luftreibung bei kleinen Geschwindigkeiten. Dort kann die Luftströmung als laminar betrachtet werden. Damit ist sie nach dem Gesetz von Stokes proportional zur Geschwindigkeit, also zur ersten zeitlichen Ableitung der Auslenkung.

F_{\mathrm {R} }=-d{\dot {x}}(t)

Im Fall einer solchen linearen Dämpfung nennt man den Proportionalitätsfaktor $d$ Dämpfungskonstante.

Lineare Dämpfung

Bei linearer Dämpfung kann die Reibung allgemein durch einen Dämpfungsterm $F_{\mathrm {R} }=-2m\gamma {\dot {x}}$ hinzugefügt werden, welcher zur Geschwindigkeit ${\dot {x}}$ proportional und entgegengesetzt ausgerichtet ist. Die Konstante $\gamma \geq 0$ wird auch als Abklingkonstante bezeichnet. Damit erhält man die Bewegungsgleichung einer linear gedämpften Schwingung als gewöhnliche lineare Differentialgleichung zweiter Ordnung:

{\ddot {x}}(t)+2\gamma {\dot {x}}(t)+\omega _{0}^{2}x(t)=0

.

$\omega _{0}$ bezeichnet die ungedämpfte Eigenkreisfrequenz des Oszillators. Mit einem Exponentialansatz $x(t)=e^{\lambda t}$ gelangt man zur allgemeinen Lösung

x(t)=e^{-\gamma t}\left(c_{1}e^{{\sqrt {\gamma ^{2}-\omega _{0}^{2}}}t}+c_{2}e^{-{\sqrt {\gamma ^{2}-\omega _{0}^{2}}}t}\right)

Dabei sind $c_{1}$ und $c_{2}$ komplexwertige Konstanten, die aus den Anfangsbedingungen bestimmt werden.

Im Falle schwacher Dämpfung ( $\gamma <\omega _{0}$ ) ergibt sich somit wie im ungedämpften Fall eine sinusförmige Schwingung, deren Amplitude jedoch exponentiell abfällt. Die Stärke dieses Abfalls wird von $\gamma$ im Exponenten der einhüllenden Exponentialfunktion bestimmt: Die Amplitude fällt im Zeitraum $\tau =1/\gamma$ auf $1/e$ der ursprünglichen Amplitude ab. Die Kreisfrequenz der Schwingung verringert sich auf $\omega _{d}={\sqrt {\omega _{0}^{2}-\gamma ^{2}}}$ .
Im Falle starker Dämpfung ( $\gamma >\omega _{0}$ ), dem sogenannten Kriechfall, bildet sich keine wirkliche Schwingung mehr aus. Vielmehr kriecht die Auslenkung gegen die Ruhelage.
Im aperiodischen Grenzfall ( $\gamma =\omega _{0}$ ) erreicht die Schwingung noch eine Maximalauslenkung ( $t=\tau$ ), fällt danach aber schneller als im Fall starker Dämpfung auf die Ruhelage zurück. Ob ein Nulldurchgang stattfindet hängt von den Anfangsbedingungen ab.[1]

Gibt man die Anfangsbedingungen $x(0)$ und ${\dot {x}}(0)$ zum Zeitpunkt $t=0$ vor, dann erhält man im Schwingfall $\omega _{0}^{2}-\gamma ^{2}>0$ die partikuläre Lösung

x(t)=e^{-\gamma t}\left(x(0)\cdot \cos(\omega _{d}t)+\left(x(0)\cdot \gamma +{\dot {x}}(0)\right){\frac {\sin(\omega _{d}t)}{\omega _{d}}}\right)

mit $\omega _{d}^{2}=\omega _{0}^{2}-\gamma ^{2}$

Für den Spezialfall $\gamma =0$ , d. h. ohne Dämpfung, vereinfacht sich die Lösung zu

x(t)=x(0)\cdot \cos(\omega _{0}t)+{\dot {x}}(0){\frac {\sin(\omega _{0}t)}{\omega _{0}}}

Für den aperiodischen Grenzfall $\omega _{0}^{2}-\gamma ^{2}=0$ ergibt sich

x(t)=\left(\left({\dot {x}}(0)+\gamma \cdot x(0)\right)\cdot t+x(0)\right)e^{-\gamma t}

Variante: Torsionsoszillator

Eine Variante des klassischen harmonischen Oszillators stellt der Torsionsoszillator dar. Anstatt einer Schraubenfeder wird hier eine Torsionsfeder beziehungsweise ein Torsionsfaden verwendet. Anstatt von Translationsbewegungen kommt es dann zu Rotationsbewegungen. Die Berechnung erfolgt prinzipiell auf dem gleichen Weg. Es wird lediglich die Masse $m$ durch das Trägheitsmoment $I$ und die Geschwindigkeit $v={\dot {x}}$ durch die Winkelgeschwindigkeit $\omega ={\dot {\varphi }}$ ersetzt.

Beschreibung in der Hamilton-Dynamik

Der ungedämpfte harmonische Oszillator im Phasenraum. Dargestellt sind drei Trajektorien mit Anfangsbedingungen unterschiedlicher Energie

Die Bewegungsgleichung des harmonischen Oszillators lässt sich auch mit der hamiltonschen Mechanik herleiten.[2] Wie oben betrachten wir eine Masse $m$ an einer Feder mit Federkonstanten $k$ . Als generalisierte Koordinate wird $x=q$ verwendet. Die Hamilton-Funktion $H$ setzt sich aus potentieller und kinetischer Energie wie folgt zusammen:

H={\frac {p^{2}}{2m}}+{\frac {m\omega _{0}^{2}q^{2}}{2}}

Mit den kanonischen Gleichungen

{\dot {p}}=-{\frac {\partial H}{\partial q}}=-m\omega _{0}^{2}q

{\dot {q}}={\frac {\partial H}{\partial p}}={\frac {p}{m}}

gelangt man zur bereits oben beschriebenen Bewegungsgleichung.

{\ddot {q}}+\omega _{0}^{2}q=0

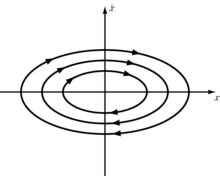
Da die Gesamt-Energie $E$ erhalten ist ( ${\frac {\partial H}{\partial t}}=0$ ), bilden Ort $q$ und Impuls $p$ eine Ellipse mit Halbachsen $a$ und $b$ aus.

{\frac {p^{2}}{2mE}}+{\frac {q^{2}}{2E/(m\omega _{0}^{2})}}=1={\frac {p^{2}}{a^{2}}}+{\frac {q^{2}}{b^{2}}}

Die Gesamt-Energie des Systems ist proportional zu der von der Ellipse eingeschlossene Fläche $A=\pi \cdot a\cdot b=2\pi E/\omega _{0}$

Im Fall eines gedämpften Oszillators bildet die Trajektorie anstelle einer Ellipse eine Spirale, die sich auf den Ursprung zubewegt.

Bei einem mehrdimensionalen harmonischen Oszillator lassen sich mittels Hauptachsentransformation $q_{i}$ und $p_{i}$ entlang der Hauptachsen des Potentials wählen. Bei einer solchen Wahl entkoppeln die Bewegungsgleichungen der einzelnen Richtungen.

Mehrdimensionaler Oszillator

Darstellung des Kraftfelds eines isotropen harmonischen Oszillators in zwei Dimensionen. Die Kraft ist durch rote Pfeile symbolisiert. Die Ruhelage ist als blauer Punkt gekennzeichnet.

Zum Beispiel mit einem Hamilton-Ansatz wie im vorherigen Abschnitt erläutert, lässt sich das Kraftgesetz für einen n-dimensionalen harmonischen Oszillator formulieren als:

m{\ddot {\mathbf {x} }}=-\sum _{i=1}^{n}k_{i}\ x_{i}\,\mathbf {e} _{i}\,.

Man sieht, dass die Differentialgleichungen entkoppelt sind, also die Kraftkomponente in einer Dimension nur von der Auslenkung in dieser Dimension abhängt. Daher sind die Lösungen für die einzelnen Komponenten des Ortsvektors die Lösungen des entsprechenden eindimensionalen Problems:

x_{i}(t)=u_{i}\,e^{\lambda _{i}\,t}+v_{i}\,e^{-\lambda _{i}\,t}

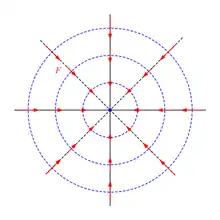
Die Eigenwerte $\textstyle \lambda _{i}=\mathrm {i} \,{\sqrt {\frac {k_{i}}{m}}}$ entsprechen dabei den Eigenkreisfrequenzen. Lassen sich alle $\lambda _{i}$ als ganzzahliges Vielfaches einer Konstanten schreiben, so ist die Schwingung des harmonischen Oszillators periodisch. Ein isotroper harmonischer Oszillator ist daher immer periodisch.

Zweidimensionaler Oszillator

Bei einem anisotropen zweidimensionalen harmonischen Oszillator bewegt sich das Teilchen auf einer Lissajous-Kurve. Die Bewegung ist periodisch, wenn die Frequenzen der Schwingungen in je einer Koordinate in einem rationalen Verhältnis stehen. Andernfalls ist sie aperiodisch, d. h. sie kehrt niemals in den Anfangszustand zurück. Sie kommt ihm aber beliebig nahe.

Bei einem isotropen zweidimensionalen harmonischen Oszillator entartet die Lissajous-Kurve zu einem Kreis, einer raumfesten geraden Strecke oder einer raumfesten Ellipse. Ein Beispiel ist das sphärische Pendel bei kleinen Auslenkungen.

Die Bewegungsgleichungen sind

{\begin{array}{ll}{\ddot {x}}&=-\omega _{0}^{2}\,x\\{\ddot {y}}&=-\omega _{0}^{2}\,y\end{array}}

Die allgemeine Lösung lässt sich schreiben als:

{\vec {r}}(t)={\begin{pmatrix}x(t)\\y(t)\end{pmatrix}}={\begin{pmatrix}c_{1}\\c_{2}\end{pmatrix}}\cos(\omega _{0}t)+{\begin{pmatrix}c_{3}\\c_{4}\end{pmatrix}}\sin(\omega _{0}t)

,

wobei die Konstanten ${\begin{pmatrix}c_{1}\\c_{2}\end{pmatrix}}={\vec {r}}(0)$ durch den Anfangsort und ${\begin{pmatrix}c_{3}\\c_{4}\end{pmatrix}}={\vec {v}}(0)/\omega _{0}$ durch die Anfangsgeschwindigkeit gegeben sind. Im Fall ${\vec {v}}(0)={\vec {0}}$ ergibt sich eine gerade Strecke. Wenn ${\vec {r}}(0)\neq {\vec {0}}$ und ${\vec {v}}(0)\neq {\vec {0}}$ und beide nicht zueinander parallel sind, ergeben sich Trajektorien in Form einer Ellipse oder Kreis, deren Mittelpunkt die Ruhelage ist.

Um die möglichen Bewegungsformen zu bestimmen, wird die allgemeine Lösung so ausgedrückt:

{\begin{pmatrix}x(t)\\y(t)\end{pmatrix}}={\begin{pmatrix}A_{x}\,\cos(\omega _{0}t-\alpha _{x})\\A_{y}\,\cos(\omega _{0}t-\alpha _{y})\end{pmatrix}}

mit beliebigen Werten für die Amplituden $A_{x},\,A_{y}$ und Phasenverschiebungen $\alpha _{x},\,\alpha _{y}$ , die sich aus den Anfangsbedingungen ergeben. Es können sich verschiedene Bahnkurven bilden, die sämtlich den Ursprung als Mittelpunkt haben und mit der gleichen Frequenz durchlaufen werden:

Für $\alpha _{x}=\alpha _{y}$ ergibt sich eine lineare harmonische Schwingung zwischen den Punkten $\textstyle \pm {\begin{pmatrix}A_{x}\\A_{y}\end{pmatrix}}$ längs einer Geraden, die mit der x-Achse den Winkel $\arctan(\alpha _{y}/\alpha _{x})$ bildet.
Für $\alpha _{x},=0,\alpha _{y}=90^{\circ }$ ergibt sich eine Ellipse mit den Halbachsen der Länge $A_{x}$ bzw. $A_{y}$ parallel zu den Koordinatenachsen. Ist dann auch noch $A_{x}=A_{y}$ , wird aus der Ellipse ein Kreis. Dann ist das Pendel ein konisches Pendel (s. o.).
Allgemein ergibt sich für $\alpha _{x}\neq \alpha _{y}$ und beliebigen Amplituden $A_{x},\,A_{y}$ eine Ellipse, deren Halbachsen von allen vier Parametern abhängen und schräg zu den Koordinatenachsen liegen.

Schreibweise mit komplexen Zahlen

Die beiden Koordinaten können zu einer einzigen komplexen Variablen

u=x+{\text{i}}y

zusammengefasst werden. Für $u$ gilt dann die Differentialgleichung

{\ddot {u}}=-\omega _{0}^{2}\,u

mit der allgemeinen Lösung

u(t)=A{\text{e}}^{\rm {{i}\omega _{0}t}}+B{\text{e}}^{-{\text{i}}\omega _{0}t}

.

Die beiden Konstanten $A,\,B$ werden aus den Anfangsbedingungen berechnet:

{\begin{array}{ll}u(0)=x(0)+{\text{i}}\,y(0)=A+B\\{\dot {u}}(0)={\dot {x}}(0)+{\text{i}}\,{\dot {y}}(0)={\text{i}}\,\omega _{0}(A-B)\end{array}}

Einfache Spezialfälle sind:

Für $B=0$ ergibt sich eine Kreisbahn im Uhrzeigersinn (mathematisch negativer Sinn) mit Radius $R=|A|$ .
Für $A=0$ ergibt sich eine Kreisbahn gegen den Uhrzeigersinn (mathematisch positiver Sinn) mit Radius $R=|B|$ .
Für $A=B\,(\neq 0)$ ergibt sich eine gerade Strecke zwischen vom Punkt ${\begin{pmatrix}2\,{\text{Re}}(A)\\2\,{\text{Im}}(A)\end{pmatrix}}$ zum Punkt ${\begin{pmatrix}-2\,{\text{Re}}(A)\\-2\,{\text{Im}}(A)\end{pmatrix}}$ (und zurück).
Für $A=-B\,(\neq 0)$ ergibt sich dieselbe gerade Strecke, aber beginnend in der Ruhelage.

Der harmonische Oszillator außerhalb der Mechanik

Elektrischer Schwingkreis

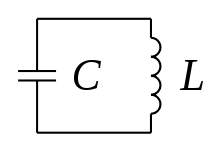
Schaltplan eines elektrischen Schwingkreises

Der elektrische Schwingkreis ist ein harmonischer Oszillator in der Elektrodynamik. Während in der Mechanik periodisch potentielle und kinetische Energie ineinander umgewandelt werden, werden im Schwingkreis die in einem Kondensator mit der Kapazität $C$ gespeicherte elektrische Energie und die in einer Spule mit der Induktivität $L$ gespeicherte magnetische Energie gegeneinander ausgetauscht. Es ergibt sich eine Differentialgleichung für die Stromstärke $i$ :

{\ddot {i}}(t)+{\frac {1}{LC}}\,i(t)=0

Die Ähnlichkeit mit der Bewegungsgleichung des mechanischen Oszillators ist offensichtlich. Folgende Tabelle soll Analogien zwischen dem mechanischen und elektrischen Oszillator deutlich machen:

mechanisch (Translation)	mechanisch (Torsion/Rotation)	RLC–Reihenschwingkreis	RLC–Parallelschwingkreis
Auslenkung $x$	Winkel $\varphi$	Ladung $q$	Spannung $u$
Geschwindigkeit ${\dot {x}}\equiv v$	Winkelgeschwindigkeit ${\dot {\varphi }}\equiv \omega$	Stromstärke ${\dot {q}}\equiv i$	Änderungsrate der Spannung ${\dot {u}}$
Masse $m$	Trägheitsmoment $I$	Induktivität $L$	Kapazität $C$
Federkonstante $k$	Torsionskonstante $\mu$	Reziproke Kapazität $1/C$	Reziproke Induktivität $1/L$
Dämpfungskonstante $d$	Dämpfungskonstante $\Gamma$	Widerstand $R$	Leitwert $1/R$
äußere Kraft $F(t)$	äußeres Drehmoment $M(t)$	externe Spannung $u_{e}(t)$	Änderungsrate der externen Stromstärke ${\dot {i}}_{e}(t)$
Ungedämpfte Eigenfrequenz $f_{0}$ :
${\frac {1}{2\pi }}{\sqrt {\frac {k}{m}}}$	${\frac {1}{2\pi }}{\sqrt {\frac {\mu }{I}}}$	${\frac {1}{2\pi }}{\sqrt {\frac {1}{LC}}}$	${\frac {1}{2\pi }}{\sqrt {\frac {1}{LC}}}$
Differentialgleichung
$m{\ddot {x}}+d{\dot {x}}+kx=F(t)$	$I{\ddot {\varphi }}+\Gamma {\dot {\varphi }}+\mu \varphi =M(t)$	$L{\ddot {q}}+R{\dot {q}}+q/C=u_{e}(t)$	$C{\ddot {u}}+{\dot {u}}/R+u/L={\dot {i}}_{e}(t)$

Der harmonische Oszillator der Quantenmechanik

Da ein beliebiges Potential um eine stabile Gleichgewichtslage entwickelt werden kann und dann in 1. Näherung parabelförmig ist, ist der harmonische Oszillator in der Quantenmechanik ein Standard-Modell. Es ist eines der wenigen Systeme, für das eine analytische Lösung bekannt ist.

In der Quantenmechanik werden die Orts-, Impuls- und Energievariablen eines Teilchens durch Operatoren ersetzt. Der Hamiltonoperator für die Energie eines harmonischen Oszillators ist gegeben durch

{\hat {H}}={\frac {{\hat {p}}^{2}}{2m}}+m\omega ^{2}{\frac {{\hat {x}}^{2}}{2}}

.

Die Wellenfunktionen, mit denen sich die Aufenthaltswahrscheinlichkeiten des Teilchens berechnen lassen, sind Eigenfunktionen des Hamiltonoperators. Die Energieniveaus entsprechen den Eigenwerten.

Lorentz-Oszillator in der Optik

Der Lorentzoszillator dient in der Optik als Modell um das Verhalten der Atome eines Festkörpers unter Einfluss einer elektromagnetischen Welle zu beschreiben. Zum Beispiel ist dann die Suszeptibilität, die dem Aufbau des Feldes entgegenwirkt, das Analogon zur Dämpfung durch Reibung in der Mechanik. Mit Hilfe des Lorentzoszillators lassen sich im Drudemodell optische Phänomene wie Doppelbrechung oder der komplexe Brechungsindex erklären.

Anregung harmonischer Oszillatoren

Wenn einem Oszillator Energie zugefügt wird, spricht man von Anregung. Für den mechanischen Oszillator bedeutet dies, dass entweder eine externe Kraft $F_{\mathrm {ext} }$ angreift, oder sich Parameter des Oszillators wie die Eigenfrequenz $\omega _{0}$ verändern. Die Anregung quantenmechanischer Oszillatoren wird mittels Leiteroperatoren dargestellt (siehe Harmonischer Oszillator (Quantenmechanik)). Das Abführen von Energie, auch Abregung genannt, geschieht analog.

Erzwungene Schwingung

Eine erzwungene Schwingung wird durch eine unabhängige, meist periodische Kraft oder auch elektrische Spannung angeregt. Ein Beispiel hierfür ist eine Dipolantenne. Die Differentialgleichung, hier das Beispiel des gedämpften Oszillators, wird dadurch inhomogen:

{\ddot {x}}(t)+2\gamma {\dot {x}}(t)+\omega _{0}^{2}x(t)={\frac {F_{\mathrm {ext} }(t)}{m}}

Selbsterregte Schwingung

Von einer selbsterregten Schwingung spricht man, wenn die Energiezufuhr durch ein geeignetes Steuerelement und den Schwingungsvorgang selbst gesteuert wird. Mathematisch lässt sich eine solche Energiezufuhr zum Beispiel durch einen speziellen Dämpfungsterm realisieren, bei dem die Dämpfung negativ werden kann. Ein solches System ist meist nichtlinear. Ein Beispiel hierfür ist der Van-der-Pol-Oszillator.

Parametererregte Schwingung

Wenn sich durch die Veränderung von Parametern, wie der Länge eines Pendels, die Eigenfrequenz $\omega _{0}$ eines harmonischen Oszillators zeitlich verändert, spricht man von einer parametererregten Schwingung. Ein Beispiel ist eine Schaukel bei kleinen Auslenkungen.

Gekoppelte harmonische Oszillatoren

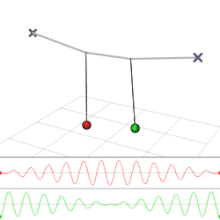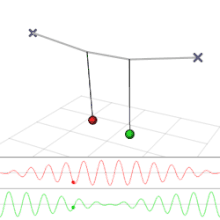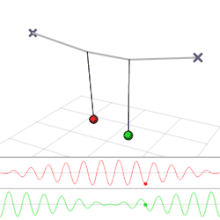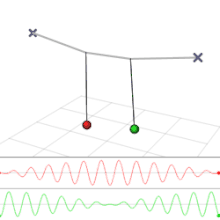
Bei zwei Pendeln, die an einer Schnur befestigt sind, wird die Energie der Schwingung periodisch zwischen beiden Pendeln übertragen.

Einen mehrdimensionalen harmonischen Oszillator, bei dem die einzelnen Komponenten, also die harmonischen Oszillatoren entlang der Hauptachsen des Potentials, nicht unabhängig sind, sondern miteinander wechselwirken, bezeichnet man als gekoppelt. Dies führt dazu, dass die Energie der Schwingung der einzelnen Komponenten nicht mehr erhalten sein muss, da sie durch die Wechselwirkung von einer Komponente auf eine andere übertragen werden kann. Dadurch kommt es zu einer Form der Amplitudenmodulation.

Gekoppelte mechanische Oszillatoren nennt man auch gekoppelte Pendel. Eine mechanische Wechselwirkung zwischen zwei Pendeln wird beispielsweise erzeugt, indem man die Massen zweier getrennter Pendel mit einer Feder verbindet. Wenn mehrere gleiche Pendel, in einer Reihe angeordnet, jeweils mit ihren unmittelbaren Nachbarn über Federn verbunden sind, bezeichnet man die Anordnung als Schwingerkette. Ein interessantes Beispiel, bei dem die Energie zwischen einer Translationsbewegung und einer Rotationsbewegung wechselt, ist das Wilberforce-Pendel.

Mit Hilfe gekoppelter Oszillatoren können auch Gitterschwingungen beispielsweise in Kristallen modelliert werden. Hier sorgt die elektrische Wechselwirkung zwischen den Ionen, Molekülen oder Atomen des Kristallgitters für die notwendige Kopplung. Die quantenmechanische Betrachtung im Artikel Harmonischer Oszillator (Quantenmechanik) führt dann zu den Phononen.

Kontinuumsübergang

Schwingungen eines Kontinuums, beispielsweise eine Saitenschwingung können mit Hilfe eines unendlich dimensionalen gekoppelten harmonischen Oszillators beziehungsweise unendlich vielen eindimensionalen gekoppelten harmonischen Oszillatoren beschrieben werden. Der Übergang zu unendlich vielen Oszillatoren wird nachfolgend für eine Longitudinalwelle durchgeführt. Das Verfahren lässt sich analog auch für Transversalwellen durchführen.

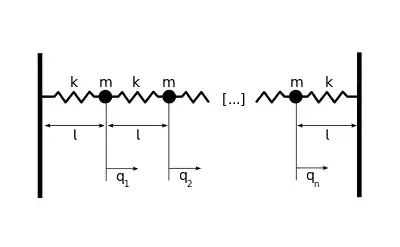
Schema eines Federschwingers mit n gekoppelten Oszillatoren

Wir nehmen das Beispiel von $n$ gekoppelten Oszillatoren der Masse $m$ , die durch Federn mit Federkonstanten $k$ verbunden sind. Die Auslenkung des i-ten Oszillators bezeichnen wir mit $q_{i}$ . Der Abstand der einzelnen Massen ist $l$ . Die Lagrange-Funktion dieses Systems ist dann:

{\mathcal {L}}={\frac {m}{2}}\sum _{i=1}^{n}{\dot {q}}_{i}^{2}-{\frac {k}{2}}\sum _{i=0}^{n}(q_{i+1}-q_{i})^{2}

Die Bewegungsgleichung des Systems lässt sich daraus herleiten als:

m{\ddot {q}}_{i}=k((q_{i+1}-q_{i})-(q_{i}-q_{i-1}))

Diese Gleichung teilen wir durch $kl^{2}$ und erhalten:

{\frac {m}{k\,l^{2}}}{\ddot {q}}_{i}={\frac {1}{l}}\left({\frac {q_{i+1}-q_{i}}{l}}-{\frac {q_{i}-q_{i-1}}{l}}\right)

Durch einen Kontinuumsübergang wird der diskrete Index $i$ durch eine kontinuierliche Koordinate $x=i\cdot l$ , und die diskrete Funktion $q_{i}(t)$ durch die Wellenfunktion $\Psi (x,t)$ ersetzt. Für einen solchen Kontinuumslimes wird gleichzeitig der Limes $n\to \infty$ , $l\to 0$ , $m\to 0$ und $k\to \infty$ genommen, sodass dabei folgende Größen konstant gehalten werden:

Die Gesamtlänge $(n+1)l$
Die Gesamtmasse $nm$ und damit auch die Dichte $m/l$
Das Produkt aus Federkonstante und Federlänge $kl$

Der Faktor ${\frac {m}{k\,l^{2}}}$ auf der linken Seite der Gleichung ist konstant. Daher lässt sich diese Seite schreiben als

{\frac {1}{c^{2}}}{\frac {\partial ^{2}\Psi }{\partial t^{2}}}

Die rechte Seite der Gleichung lässt sich umschreiben als:

\lim _{l\to 0}{\frac {1}{l}}\left({\frac {\Psi (x+l,t)-\Psi (x,t)}{l}}-{\frac {\Psi (x,t)-\Psi (x-l,t)}{l}}\right)

Dies ist gerade der Differenzenquotient für die zweite Ableitung. Man erhält nämlich mit Hilfe einer Taylorentwicklung um $x$

\lim _{l\to 0}\left({\frac {\Psi (x+l,t)-2\Psi (x,t)+\Psi (x-l,t)}{l^{2}}}\right)=\lim _{l\to 0}{\frac {1}{l^{2}}}\left({\frac {\partial ^{2}\Psi }{\partial x^{2}}}(x,t)\cdot l^{2}+{\mathcal {O}}(l^{4})\right)={\frac {\partial ^{2}\Psi }{\partial x^{2}}}(x,t)

Man erhält so die Wellengleichung

\left({\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}-{\frac {\partial ^{2}}{\partial x^{2}}}\right)\Psi =0

Weblinks

Commons: Harmonischer Oszillator – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

Wolfgang Demtröder: Experimentalphysik 1. 4. Auflage. Springer, Berlin/Heidelberg 2006, ISBN 3-540-26034-X, S. 335–357.
Wolfgang Nolting: Theoretische Physik 2. 7. Auflage. Springer, Berlin/Heidelberg 2006, ISBN 3-540-30660-9, S. 103–104.

Anmerkungen

Zeitpunktangaben beziehen sich auf obenstehende Grafik; der Abstand zweier Zeitpunkte beträgt eine viertel Periode, also ${\frac {\pi }{2}}{\sqrt {m/k}}$ .

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[2] Wolfgang Demtröder: Experimentalphysik 1. 4. Auflage. Springer, Berlin/Heidelberg 2006, ISBN 3-540-26034-X, S. 335–357.

[3] Wolfgang Nolting: Theoretische Physik 2. 7. Auflage. Springer, Berlin/Heidelberg 2006, ISBN 3-540-30660-9, S. 103–104.

[1] Zeitpunktangaben beziehen sich auf obenstehende Grafik; der Abstand zweier Zeitpunkte beträgt eine viertel Periode, also ${\frac {\pi }{2}}{\sqrt {m/k}}$ .