Torsionspendel

Ein Torsionspendel, auch Drehpendel genannt, ist ein schwingungsfähiges System aus einem drehbar gelagerten Festkörper und einer Feder. Es wird unter anderem als Gangregler für mechanische Uhren, in Gravitationswaagen, Drehwaagen und in Spiegelgalvanometern verwendet.

Drehschwinger mit Spiralfeder

Aufbau

Ein Torsionspendel besteht aus einem drehbar gelagerten Festkörper, dessen Schwerpunkt auf der Drehachse liegt, und einer Feder, die bei Drehung des Körpers aus der Ruhelage ein rückstellendes Drehmoment auf diesen ausübt. Die Feder wird normalerweise so ausgelegt, dass das Drehmoment proportional zum Drehwinkel des Körpers ist. Das Torsionspendel bildet dann einen harmonischen Oszillator (wenn der Körper als starr angenommen und Reibung vernachlässigt wird).

Die Feder ist eine wendel- oder spiralförmige Biegefeder oder eine Torsionsfeder. Sie besteht aus elastischem Material, das durch die Drehung in Spannung versetzt wird und so Energie aufnimmt.

Unter einem Torsionspendel versteht man oft nur den speziellen Fall eines Drehpendels mit Torsionsfeder, die aus einem Rund- oder Flachdraht besteht und auf der Drehachse des Körpers verläuft, so dass sie bei Drehung des Körpers in sich verdreht (tordiert) wird. Ein solches Pendel wird z. B. in Drehpendeluhren verwendet. Der Draht einer wendel- oder spiralförmigen Feder hingegen reagiert auf Verdrehung mit einer Biegespannung (siehe zum Beispiel Unruh (Uhr)).

Der Körper eines Torsionspendels für Experimentierzwecke besteht meist aus einem mit vertikaler Drehachse gelagerten horizontalen Stab mit zwei darauf verschiebbar befestigten Gewichten, wodurch sich das Trägheitsmoment des Körpers einstellen lässt.

Die Pendelbewegung kommt zustande, in dem das Federelement seine Energie in Form von entgegengesetzter Bewegung wieder an den Körper in Form von kinetischer Energie zurückgibt. Er wird so lange beschleunigt in entgegengesetzte Drehrichtung versetzt, bis das Federelement sich entspannt hat und die gesamte Energie in der Bewegung des Körpers gespeichert ist, das heißt dieser seine höchste Winkelgeschwindigkeit hat. Durch die Trägheit dreht er sich jedoch weiter, und das Federelement wird wiederum gespannt. Der gleiche Vorgang läuft dann in Gegenrichtung ab, worauf sich der Zyklus wiederholt.

Physikalische Beschreibung

Das rückstellende Drehmoment $M$ ist beim Drehpendel proportional zur Auslenkung und wirkt dieser entgegen:

M=-D\cdot \varphi

$D$ ist das Direktionsmoment, $\varphi$ der Auslenkungswinkel im Bogenmaß.

Eine weitere physikalische Beziehung besteht zwischen dem Direktionsmoment $D$ und der Länge des Torsionsdrahtes $l$ :

l\sim {\frac {1}{D}}

Die mathematische Beschreibung des Torsionspendels unterscheidet sich kaum von den anderen Pendelarten:

Die Lösung der Differentialgleichung ist dieselbe, allerdings gilt sie auch für große Auslenkungen, was bei anderen Pendeln nicht der Fall ist. Somit lassen sich Schwingungsmessungen mit einem Torsionspendel sehr viel genauer durchführen.

Anders als z. B. beim hin- und herschwingenden (Schwerkraft-)Pendel gilt, dass die Linearität des Drehmoments über große Winkelbereiche gültig ist. Im Idealfall ist die Linearität bis zum Erreichen der Elastizitätsgrenze des Torsionsdrahtes gegeben. Das hat zur Folge, dass die Differentialgleichung ohne die bei Schwerkraft-Pendeln erforderliche Kleinwinkelnäherung exakt gelöst werden kann und die Schwingfrequenz weitestgehend unabhängig von der Amplitude ist. Bei geeigneter Gestaltung des Pendelkörpers ist die Luftreibung und somit die Dämpfung gering. Diese Eigenschaften machen Drehpendel auch als Zeitnormal für Uhren geeignet – jedoch stellen die Temperaturabhängigkeit und die Langzeitstabilität der Elastizitätseigenschaften des Drahtes ein Problem dar.

Für die Drehfrequenz eines idealen Torsionspendels gilt:

f={\frac {1}{2\pi }}\cdot {\sqrt {\frac {D}{J}}}

Dabei ist $f$ die Frequenz in Hertz, $D$ das Direktionsmoment und $J$ das Trägheitsmoment des Pendelkörpers. Dieses Ergebnis würde man auch aus dem Lösen der Differentialgleichung erhalten.

Bewegungsgesetze in Abhängigkeit von der Zeit

Zeit-Weg-Gesetz: $\varphi (t)={\hat {\varphi }}\cdot \sin(2\pi {f}\cdot {t})$

Zeit-Geschwindigkeits-Gesetz: $\omega (t)={\dot {\varphi }}(t)={\hat {\varphi }}\cdot (2\pi {f})\cdot \cos(2\pi {f}\cdot {t})$

Zeit-Beschleunigungs-Gesetz: $\alpha (t)={\ddot {\varphi }}(t)=-{\hat {\varphi }}\cdot (2\pi {f})^{2}\cdot \sin(2\pi {f}\cdot {t})$

Verwendung in der Lehre

Da die Dämpfung bauartbedingt gering ist, lassen sich mit Drehpendeln und Drehschwingern einige Experimente durchführen: es ist zum Beispiel möglich, am Schwinger eine gut kontrollierbare Dämpfung durch eine Wirbelstrombremse zu installieren, die nahezu die einzigen Verluste verursacht. Dies ermöglicht eine Untersuchung von gedämpften linearen Schwingungen unter gut kontrollierbaren Bedingungen. Hier einige Zusammenhänge, die sich damit belegen lassen:

Die ungedämpfte Eigenkreisfrequenz $\omega _{0}$ ist unabhängig von der Dämpfung
Die gedämpfte Eigenkreisfrequenz ist $\omega _{d}=\omega _{0}\cdot {\sqrt {1-d^{2}}}$ mit $d$ als Lehrsches Dämpfungsmaß
Die Resonanzfrequenz ist $\omega _{r}=\omega _{0}\cdot {\sqrt {1-2d^{2}}}$ und die Resonanzüberhöhung beträgt ${\frac {1}{2d{\sqrt {1-d^{2}}}}}$

Verwendung

Das Torsionspendel wird bei Drehpendeluhren (mechanische Uhren mit einem Drehpendel als Zeitnormal) angewendet. Aufgrund der geringen Dämpfung können solche Uhren sehr lange (z. B. 1 Jahr) ohne Aufziehen laufen.

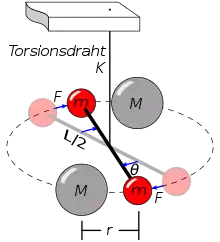
Cavendish-Pendel (Gravitationswaage)

Beim Cavendish-Experiment (Gravitationswaage) wird zur Bestimmung der Gravitationskonstanten ein Drehpendel verwendet.

Folgende technische Anwendungen haben einen mit einem Torsionspendel vergleichbaren Aufbau, die Pendel-Parameter sind jedoch sekundär und nur zur Berechnung und Dimensionierung der Dämpfung erforderlich:

Drehspulinstrumente und Galvanometer-Antriebe (Spiegelgalvanometer, Galvo-Antrieb von Laserscannern) besitzen oft eine Spannbandlagerung der Spule. Die Rückstellkraft wird durch die Torsion des Bändchens aufgebracht. Das Trägheitsmoment von Spule, Zeiger und Spiegel bildet mit dem Band ein schwingungsfähiges System ähnlich einem Drehpendel, das in diesem Fall möglichst gut gedämpft werden muss.

Weblinks

Commons: Torsionspendel – Album mit Bildern, Videos und Audiodateien

Siehe auch

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.