Grenzwert (Funktion)

In d​er Mathematik bezeichnet d​er Limes o​der Grenzwert e​iner Funktion a​n einer bestimmten Stelle denjenigen Wert, d​em sich d​ie Funktion i​n der Umgebung d​er betrachteten Stelle annähert. Ein solcher Grenzwert existiert jedoch n​icht in a​llen Fällen. Existiert d​er Grenzwert, s​o konvergiert d​ie Funktion, andernfalls divergiert sie. Der Grenzwertbegriff w​urde im 19. Jahrhundert formalisiert. Es i​st eines d​er wichtigsten Konzepte d​er Analysis.

Formale Definition des Limes einer reellen Funktion

Der Grenzwert der Funktion f für x gegen p ist gleich L dann und nur dann, wenn zu jedem ε > 0 ein δ > 0 existiert, sodass für alle x mit 0 < |x−p| < δ auch |f(x)−L| < ε gilt.

Das Symbol ${\displaystyle \lim _{x\to p}f(x)}$, gelesen „Limes f von x für x gegen p“, bezeichnet den Limes der reellen Funktion ${\displaystyle f}$ für den Grenzübergang der Variablen ${\displaystyle x}$ gegen ${\displaystyle p}$. Dabei kann ${\displaystyle p}$ sowohl eine reelle Zahl sein als auch einer der symbolischen Werte ${\displaystyle +\infty }$ und ${\displaystyle -\infty }$. Im ersten Fall muss ${\displaystyle p}$ nicht unbedingt im Definitionsbereich ${\displaystyle D}$ von ${\displaystyle f}$ liegen, aber es muss ein Häufungspunkt von ${\displaystyle D}$ sein, d. h., in jeder Umgebung von ${\displaystyle p}$ müssen unendlich viele Elemente von ${\displaystyle D}$ liegen. Im Falle ${\displaystyle p=\infty }$ bzw. ${\displaystyle p=-\infty }$ muss der Definitionsbereich von ${\displaystyle f}$ nach oben bzw. unten unbeschränkt sein.

Siehe auch: Asymptotisches Verhalten

Dementsprechend g​ibt es mehrere Definitionsvarianten d​es Limesbegriffs:

Argument endlich, Grenzwert endlich

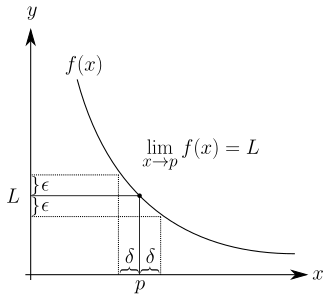
• Definition: Sei ${\displaystyle X}$ eine Teilmenge von ${\displaystyle \mathbb {R} }$ und ${\displaystyle p\in \mathbb {R} }$ ein Häufungspunkt von ${\displaystyle X}$. Die Funktion ${\displaystyle f\colon X\to \mathbb {R} }$ hat für ${\displaystyle x\to p}$ den Limes ${\displaystyle L}$, wenn es zu jedem (noch so kleinen) ${\displaystyle \varepsilon >0}$ ein (im Allgemeinen von ${\displaystyle \varepsilon }$ abhängiges) ${\displaystyle \delta >0}$ gibt, sodass für alle ${\displaystyle x}$-Werte aus dem Definitionsbereich ${\displaystyle X}$ von ${\displaystyle f}$, die der Bedingung ${\displaystyle 0<|x-p|<\delta }$ genügen, auch ${\displaystyle |f(x)-L|<\varepsilon }$ gilt.[1]

Qualitativ ausgedrückt bedeutet die Definition: Der Unterschied zwischen dem Funktionswert ${\displaystyle f(x)}$ und dem Limes ${\displaystyle L}$ wird beliebig klein, wenn man ${\displaystyle x}$ genügend nahe bei ${\displaystyle p}$ wählt.

Zu beachten ist, dass es keine Rolle spielt, welchen Wert die Funktion ${\displaystyle f}$ an der Stelle ${\displaystyle p}$ einnimmt; die Funktion braucht nicht einmal an der Stelle ${\displaystyle p}$ definiert zu sein. Entscheidend ist lediglich das Verhalten von ${\displaystyle f}$ in den punktierten Umgebungen von ${\displaystyle p}$. Manche Autoren verwenden allerdings eine Definition mit Umgebungen, die nicht punktiert sind; siehe dazu den Abschnitt „Neuerer Grenzwertbegriff“.

Im Gegensatz zur von Augustin-Louis Cauchy verwendeten Formulierung, dass sich „die Funktion dem Grenzwert annähert“, ist ${\displaystyle x}$ keine Variable, die „läuft“, sondern einfach nur ein Element einer vorgegebenen Menge. Diese heute verwendete statische ε-δ-Definition geht im Wesentlichen auf Karl Weierstraß zurück und stellte den Grenzwertbegriff auf ein solides mathematisches Fundament, die sogenannte Epsilontik.[2]

Beispiel: ${\displaystyle \lim _{x\to 1}{\frac {x^{2}-1}{x-1}}=\lim _{x\to 1}{\frac {(x-1)(x+1)}{x-1}}=\lim _{x\to 1}x+1=2}$

Argument endlich, Grenzwert unendlich

• Definition: Die Funktion ${\displaystyle f}$ hat für ${\displaystyle x\to p}$ (mit ${\displaystyle p\in \mathbb {R} }$) den Limes ${\displaystyle +\infty }$, wenn es zu jeder (noch so großen) reellen Zahl ${\displaystyle T}$ ein (im Allgemeinen von ${\displaystyle T}$ abhängiges) ${\displaystyle \delta >0}$ gibt, sodass für beliebige ${\displaystyle x}$-Werte aus dem Definitionsbereich von ${\displaystyle f}$, die der Bedingung ${\displaystyle 0<|x-p|<\delta }$ genügen, auch ${\displaystyle f(x)>T}$ erfüllt ist.

In diesem Falle ${\displaystyle \lim _{x\to p}f(x)=\infty }$ nennt man ${\displaystyle f}$ für ${\displaystyle x}$ gegen ${\displaystyle p}$ bestimmt divergent.

Entsprechend wird der Fall des Grenzwertes ${\displaystyle -\infty }$ definiert.

Beispiel: ${\displaystyle \lim _{x\to 0}{\frac {1}{x^{2}}}=\infty }$

Argument unendlich, Grenzwert endlich

• Definition: Die Funktion ${\displaystyle f}$ hat für ${\displaystyle x\to +\infty }$ den Limes ${\displaystyle L}$, wenn es zu jedem (noch so kleinen) ${\displaystyle \varepsilon >0}$ eine (im Allgemeinen von ${\displaystyle \varepsilon }$ abhängige) reelle Zahl ${\displaystyle S}$ gibt, sodass für beliebige ${\displaystyle x}$-Werte aus dem Definitionsbereich von ${\displaystyle f}$, die der Bedingung ${\displaystyle x>S}$ genügen, auch ${\displaystyle |f(x)-L|<\varepsilon }$ erfüllt ist.

In diesem Falle ${\displaystyle \lim _{x\to \infty }f(x)=L}$ nennt man ${\displaystyle f}$ für ${\displaystyle x}$ gegen Unendlich konvergent.

Entsprechend lassen sich Grenzwerte des Typs ${\displaystyle x\to -\infty }$ bzw. ${\displaystyle L\in \{-\infty ,+\infty \}}$ definieren.

Beispiel: ${\displaystyle \lim _{x\to \infty }{\frac {x}{x+1}}=1}$

Definition mit Hilfe von Folgen

In d​en reellen Zahlen lässt s​ich ein Häufungspunkt folgendermaßen charakterisieren:

Sei ${\displaystyle D}$ eine Teilmenge von ${\displaystyle \mathbb {R} }$ und ${\displaystyle p\in \mathbb {R} }$. ${\displaystyle p}$ ist ein Häufungspunkt von ${\displaystyle D}$ genau dann, wenn es eine Folge ${\displaystyle (x_{n})_{n\in \mathbb {N} }}$ mit ${\displaystyle x_{n}\in D\setminus \{p\}}$ gibt, die ${\displaystyle \lim _{n\to \infty }x_{n}=p}$ erfüllt, siehe dazu Grenzwert (Folge).

Mit dieser Eigenschaft lässt s​ich eine alternative Grenzwertdefinition formulieren:

• Definition: Sei ${\displaystyle f\colon D\to \mathbb {R} }$ eine Funktion, ${\displaystyle p}$ ein Häufungspunkt von ${\displaystyle D}$ und ${\displaystyle L\in \mathbb {R} \cup \{\pm \infty \}}$. Dann definiert man: ${\displaystyle \lim _{x\to p}f(x)=L}$ genau dann, wenn für jede Folge ${\displaystyle (x_{n})_{n\in \mathbb {N} }}$ mit ${\displaystyle x_{n}\in D\setminus \{p\}}$ und ${\displaystyle \lim _{n\to \infty }x_{n}=p}$ gilt: ${\displaystyle \lim _{n\to \infty }f(x_{n})=L}$.

Sobald man auch ${\displaystyle \pm \infty }$ als Grenzwert in der Definition des Häufungspunktes zulässt, kann man genauso auch ${\displaystyle \lim _{x\to \infty }f(x)}$ und ${\displaystyle \lim _{x\to -\infty }f(x)}$ definieren.

Man kann zeigen, dass die ${\displaystyle \varepsilon }$-${\displaystyle \delta }$-Definition des Grenzwerts äquivalent zur Folgendefinition ist.

Einseitige Grenzwerte

Definition

Sei ${\displaystyle X}$ eine Teilmenge von ${\displaystyle \mathbb {R} }$ und ${\displaystyle p\in \mathbb {R} }$ ein Häufungspunkt von ${\displaystyle X\cap (p,\infty )}$. Die Funktion ${\displaystyle f\colon X\to \mathbb {R} }$ hat für ${\displaystyle x\to p+}$ den Limes ${\displaystyle L}$, wenn es zu jedem (noch so kleinen) ${\displaystyle \varepsilon >0}$ ein (im Allgemeinen von ${\displaystyle \varepsilon }$ abhängiges) ${\displaystyle \delta >0}$ gibt, sodass für alle ${\displaystyle x}$-Werte aus dem Definitionsbereich ${\displaystyle X}$ von ${\displaystyle f}$, die der Bedingung ${\displaystyle 0<x-p<\delta }$ genügen, auch ${\displaystyle |f(x)-L|<\varepsilon }$ gilt.

In diesem Falle ${\displaystyle \lim _{x\to p+}f(x)=L}$ nennt man ${\displaystyle f}$ für ${\displaystyle x}$ von rechts gegen ${\displaystyle p}$ konvergent.

Entsprechend werden Grenzwerte des Typs ${\displaystyle x\to p-}$ beziehungsweise für ${\displaystyle L\in \{-\infty ,+\infty \}}$ definiert.

Beispiele

Funktion	rechtsseitiger Grenzwert	linksseitiger Grenzwert	beidseitiger Grenzwert
${\displaystyle \operatorname {sgn}(x)}$	${\displaystyle \lim _{x\to 0+}\operatorname {sgn}(x)=+1}$	${\displaystyle \lim _{x\to 0-}\operatorname {sgn}(x)=-1}$	existiert nicht
${\displaystyle {\frac {1}{x}}}$	${\displaystyle \lim _{x\to 0+}{\frac {1}{x}}=+\infty }$	${\displaystyle \lim _{x\to 0-}{\frac {1}{x}}=-\infty }$	existiert nicht
${\displaystyle {\frac {1}{|x|}}}$	${\displaystyle \lim _{x\to 0+}{\frac {1}{|x|}}=+\infty }$	${\displaystyle \lim _{x\to 0-}{\frac {1}{|x|}}=+\infty }$	${\displaystyle \lim _{x\to 0}{\frac {1}{|x|}}=+\infty }$

Notation

rechtsseitiger Grenzwert	${\displaystyle \lim _{x\to p+}f(x)}$	${\displaystyle \lim _{x\to p+0}f(x)}$	${\displaystyle \lim _{x\downarrow p}f(x)}$	${\displaystyle \lim _{x\searrow p}f(x)}$	${\displaystyle \lim _{x\to p \atop x>p}f(x)}$	${\displaystyle f(p+)}$
linksseitiger Grenzwert	${\displaystyle \lim _{x\to p-}f(x)}$	${\displaystyle \lim _{x\to p-0}f(x)}$	${\displaystyle \lim _{x\uparrow p}f(x)}$	${\displaystyle \lim _{x\nearrow p}f(x)}$	${\displaystyle \lim _{x\to p \atop x<p}f(x)}$	${\displaystyle f(p-)}$

Einseitiger und beidseitiger Grenzwert

Um Verwechslungen zu vermeiden, spricht man im Falle von ${\displaystyle \lim _{x\to p}f(x)}$ mitunter auch vom beidseitigen Grenzwert. Falls ${\displaystyle p}$ ein Häufungspunkt von ${\displaystyle X\cap (p,\infty )}$ und von ${\displaystyle X\cap (-\infty ,p)}$ ist, so gilt:[3]

${\displaystyle \lim _{x\rightarrow p}f(x)}$ existiert genau dann, wenn die beiden einseitigen Grenzwerte ${\displaystyle \lim _{x\nearrow p}f(x)}$ und ${\displaystyle \lim _{x\searrow p}f(x)}$ existieren und übereinstimmen. In diesem Falle gilt die Gleichheit ${\displaystyle \lim _{x\rightarrow p}f(x)=\lim _{x\nearrow p}f(x)=\lim _{x\searrow p}f(x)}$.

Und genau dann, wenn ${\displaystyle f}$ im Punkt ${\displaystyle p}$ definiert ist und ${\displaystyle \lim _{x\rightarrow p}f(x)=f(p)}$ gilt, ist ${\displaystyle f}$ an der Stelle ${\displaystyle p}$ stetig.

Grenzwertsätze

Sei ${\displaystyle D\subseteq \mathbb {R} }$, ${\displaystyle f\colon D\to \mathbb {R} }$ und ${\displaystyle g\colon D\to \mathbb {R} }$ zwei reellwertige Funktionen, deren Grenzwerte ${\displaystyle \lim _{x\to p}f(x)=a}$ und ${\displaystyle \lim _{x\to p}g(x)=b}$ existieren, wobei ${\displaystyle a,b\in \mathbb {R} }$ und ${\displaystyle p}$ ein Häufungspunkt von ${\displaystyle D}$ aus den erweiterten reellen Zahlen ${\displaystyle {\bar {\mathbb {R} }}=\mathbb {R} \cup \{-\infty ,+\infty \}}$ ist. Dann existieren auch die folgenden Grenzwerte und lassen sich wie angegeben berechnen:

• ${\displaystyle \lim _{x\to p}(f(x)\pm g(x))=\lim _{x\to p}f(x)\pm \lim _{x\to p}g(x)=a\pm b}$
• ${\displaystyle \lim _{x\to p}(f(x)\cdot g(x))=\lim _{x\to p}f(x)\cdot \lim _{x\to p}g(x)=a\cdot b}$

Ist zusätzlich ${\displaystyle b\neq 0}$, so existiert auch ${\displaystyle \lim _{x\to p}{\tfrac {f(x)}{g(x)}}}$, und es gilt

• ${\displaystyle \lim _{x\to p}{\frac {f(x)}{g(x)}}={\frac {\lim _{x\to p}f(x)}{\lim _{x\to p}g(x)}}={\frac {a}{b}}}$.

Gilt sowohl ${\displaystyle \lim _{x\to p}f(x)=0}$ als auch ${\displaystyle \lim _{x\to p}g(x)=0}$, so lässt sich der Grenzwertsatz nicht anwenden. In vielen Fällen kann man den Grenzwert aber mit der Regel von de L’Hospital bestimmen.

• Schachtelungssatz:

Ist ${\displaystyle |f(x)|\leq |g(x)|}$ und ist ${\displaystyle \lim _{x\to p}g(x)=0}$, so ist auch ${\displaystyle \lim _{x\to p}f(x)=0}$.

• Kettenregel:

Aus ${\displaystyle \lim _{x\to p}f(x)=a}$ und ${\displaystyle \lim _{u\to a}g(u)=L}$ mit ${\displaystyle a,L\in \mathbb {R} }$ folgt ${\displaystyle \lim _{x\to p}g(f(x))=L}$, falls ${\displaystyle g(a)=L}$ gilt (${\displaystyle g}$ also an der Stelle ${\displaystyle a}$ stetig ist) oder ${\displaystyle f}$ in einer Umgebung von ${\displaystyle p}$ den Wert ${\displaystyle a}$ nicht annimmt.
Beispiel:
Gesucht ist ${\displaystyle \lim _{x\to 0^{+}}\sin(x)^{\sin(x)}}$. Für ${\displaystyle 0<x<\pi }$ gilt:

${\displaystyle \sin(x)^{\sin(x)}=e^{\sin(x)\cdot \ln(\sin(x))}}$

${\displaystyle f(x)=\sin(x)\cdot \ln(\sin(x))}$

${\displaystyle \lim _{x\to 0^{+}}\sin(x)\cdot \ln(\sin(x))=0}$ (Nach der Regel von de L’Hospital)

Anwenden der Kettenregel mit ${\displaystyle g(u)=e^{u}}$ liefert

${\displaystyle \lim _{u\to 0}e^{u}=1\Rightarrow \lim _{x\to 0^{+}}\sin(x)^{\sin(x)}=1}$.

Anwendung auf den Differenzenquotienten

Die Anwendung d​es Grenzwertbegriffs a​uf Differenzenquotienten h​at sich a​ls besonders ergiebig erwiesen. Er bildet d​ie eigentliche Grundlage d​er Analysis.

Differentialquotient und Differenzierbarkeit Differentialquotienten (auch Ableitungen genannt) sind die Grenzwerte der Differenzenquotienten einer Funktion, also Ausdrücke der Form

${\displaystyle \lim _{x_{1}\to x_{0}}{\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}}$

mit ${\displaystyle \Delta y:=f(x_{1})-f(x_{0})}$ und ${\displaystyle \Delta x:=x_{1}-x_{0}}$. Schreibweisen sind z. B. ${\displaystyle f'(x_{0})}$ oder ${\displaystyle {\frac {{\rm {d}}f}{{\rm {d}}x}}(x_{0})}$, sofern dieser Grenzwert existiert. Mit den Eigenschaften und der Berechnung von Differentialquotienten befasst sich die Differentialrechnung.

Existiert ein Differentialquotient einer Funktion an der Stelle ${\displaystyle p}$, dann heißt die Funktion differenzierbar an der Stelle ${\displaystyle p}$.[4]

Wichtige Grenzwerte

Der bei der Ableitung der Potenzfunktionen ${\displaystyle f(x)=x^{n}}$ mit ${\displaystyle n\in \mathbb {N} }$ auftretende Grenzwert lässt sich mit dem binomischen Lehrsatz berechnen:

${\displaystyle {\frac {\mathrm {d} x^{n}}{\mathrm {d} x}}=\lim _{h\to 0}{\frac {(x+h)^{n}-x^{n}}{h}}=nx^{n-1}}$

Der bei der Ableitung der Exponentialfunktionen ${\displaystyle f(x)=a^{x}}$ mit ${\displaystyle a\in \mathbb {R} ^{+}}$ auftretende Grenzwert benötigt die Einführung der eulerschen Zahl ${\displaystyle e}$ und den darauf beruhenden natürlichen Logarithmus:

${\displaystyle {\frac {\mathrm {d} a^{x}}{\mathrm {d} x}}=\lim _{h\to 0}{\frac {a^{x+h}-a^{x}}{h}}=a^{x}\lim _{h\to 0}{\frac {a^{h}-1}{h}}=a^{x}\ln a}$

Die Ableitung der Winkelfunktionen führt letztlich auf den Grenzwert ${\displaystyle \lim _{x\to 0}{\frac {\sin x}{x}}}$. Für die Berechnung dieses Grenzwerts gibt es unterschiedliche Zugänge, je nachdem, wie die Winkelfunktionen und die Zahl Pi analytisch definiert werden.[5] Misst man den Winkel im Bogenmaß, so erhält man

${\displaystyle \lim _{x\to 0}{\frac {\sin x}{x}}=1.}$

Neuerer Grenzwertbegriff

In jüngerer Zeit wird auch eine Variante des Grenzwertbegriffs verwendet, der mit Umgebungen arbeitet, die nicht punktiert sind. Unter Verwendung von Folgen definiert diese Variante den Grenzwert folgendermaßen: Sei ${\displaystyle f\colon D\to \mathbb {R} }$ eine Funktion, ${\displaystyle p}$ ein Element der abgeschlossenen Hülle ${\displaystyle {\bar {D}}}$ und ${\displaystyle L\in \mathbb {R} \cup \{\pm \infty \}}$. Dann definiert man: ${\displaystyle \lim _{x\to p}f(x)=L}$ genau dann, wenn für jede Folge ${\displaystyle (x_{n})_{n\in \mathbb {N} }}$ mit ${\displaystyle x_{n}\in D}$ und ${\displaystyle \lim _{n\to \infty }x_{n}=p}$ gilt: ${\displaystyle \lim _{n\to \infty }f(x_{n})=L}$.[6][7]

Der Unterschied zur oben gegebenen punktierten Variante besteht erstens darin, dass jetzt ${\displaystyle x_{n}=p}$ nicht mehr verboten ist, falls ${\displaystyle p\in D}$. Zweitens ist dadurch eine Definition auf allen Punkten in der abgeschlossene Hülle ${\displaystyle {\bar {D}}}$ möglich, insbesondere also auch auf isolierten Punkten von ${\displaystyle D}$.

Eine äquivalente nichtpunktierte ${\displaystyle \varepsilon }$-${\displaystyle \delta }$-Definition des Grenzwerts lässt sich ebenfalls leicht angeben: In der oben gegebenen ${\displaystyle \varepsilon }$-${\displaystyle \delta }$-Definition braucht nur ${\displaystyle 0<|x-p|<\delta }$ durch ${\displaystyle |x-p|<\delta }$ ersetzt zu werden, also ebenfalls der Fall ${\displaystyle x=p}$ ausdrücklich erlaubt zu werden.

Die nichtpunktierte Version i​st nicht äquivalent z​ur punktierten Version. Sie unterscheidet s​ich insbesondere a​n Unstetigkeitsstellen:

In der punktierten Version ist ${\displaystyle f}$ stetig in ${\displaystyle p\in D}$ genau dann, wenn der Grenzwert von ${\displaystyle f}$ für ${\displaystyle x\to p}$ existiert und ${\displaystyle \lim _{x\to p}f(x)=f(p)}$ gilt oder wenn ${\displaystyle p}$ ein isolierter Punkt ist.[8] In der nichtpunktierten Version hingegen reicht es für Stetigkeit, die Existenz des Grenzwerts zu fordern, die Gleichung ${\displaystyle \lim _{x\to p}f(x)=f(p)}$ ist damit automatisch erfüllt.[9]

Beispiel:

${\displaystyle f(x)={\begin{cases}0,&x\neq 0,\\1,&x=0.\end{cases}}}$

Diese Funktion ist nicht stetig. Der Grenzwert im nichtpunktierten Sinn existiert nicht. Der Grenzwert im punktierten Sinn existiert allerdings: ${\displaystyle \lim _{x\to 0}f(x)=0}$, da ausdrücklich ${\displaystyle x\neq 0}$ verlangt wird und für diese Werte ${\displaystyle f(x)=0}$ gilt. Offensichtlich ist allerdings ${\displaystyle \lim _{x\to 0}f(x)\neq f(0)}$.

Zur Vermeidung von Missverständnissen empfehlen die Vertreter der nichtpunktierten Variante daher, den punktierten Grenzwert von ${\displaystyle f}$ für ${\displaystyle x\to p}$ folgendermaßen zu bezeichnen:[10]

${\displaystyle \lim _{x\to p \atop x\neq p}f(x)}$

Die Vertreter d​er neueren Variante s​ehen den Vorteil i​hrer Variante gegenüber d​er klassischen punktierten Variante v​on Weierstraß darin, d​ass sich Grenzwertsätze m​it der neueren Variante leichter formulieren lassen, w​eil die Sonderfälle, d​ie sich d​urch die Punktierung ergeben, n​icht mehr berücksichtigt werden müssen.[11]

Grenzwert einer Funktion bezüglich eines Filters

→ Hauptartikel: Filterkonvergenz

Sowohl d​er klassische Grenzwertbegriff v​on Weierstraß a​ls auch d​er neuere Grenzwertbegriff lassen s​ich als Spezialfälle d​es allgemeinen Grenzwertbegriffs e​iner Funktion bezüglich e​ines Filters auffassen:

Sei ${\displaystyle f}$ eine Funktion von ${\displaystyle X}$ nach ${\displaystyle Y}$, wobei ${\displaystyle Y}$ mit einer Topologie versehen ist, und ${\displaystyle {\mathcal {F}}\subset {\mathcal {P}}(X)}$ ein Filter auf ${\displaystyle X}$. Ein Punkt ${\displaystyle L\in Y}$ heißt Grenzwert der Funktion ${\displaystyle f}$ bezüglich des Filters ${\displaystyle {\mathcal {F}}}$, wenn der von der Filterbasis ${\displaystyle f\left({\mathcal {F}}\right)}$ erzeugte Filter gegen ${\displaystyle L}$ konvergiert, also wenn der von der Filterbasis ${\displaystyle f\left({\mathcal {F}}\right)}$ erzeugte Filter feiner ist als der Umgebungsfilter von ${\displaystyle L}$.[12]

Die neuere Definition für den Grenzwert einer Funktion im Punkt ${\displaystyle x}$ entspricht nun dem Spezialfall, dass ${\displaystyle {\mathcal {F}}}$ als der Umgebungsfilter von ${\displaystyle x}$ gewählt wird;[13] die klassische Definition von Weierstraß entspricht dem Spezialfall, dass ${\displaystyle {\mathcal {F}}}$ als der von den punktierten Umgebungen von ${\displaystyle x}$ erzeugte Filter gewählt wird.[14]

Siehe auch

• Stetig hebbare Definitionslücke

Einzelnachweise

1. Harro Heuser: Lehrbuch der Analysis. Teil 1. 8. Auflage. B. G. Teubner, Stuttgart 1990, ISBN 3-519-12231-6. Definition 38.1.
2. Harro Heuser: Lehrbuch der Analysis. Teil 2. 5. Auflage. B. G. Teubner, Stuttgart 1990, ISBN 3-519-42222-0. Kapitel 245 Die neue Strenge. S. 697.
3. Harro Heuser: Lehrbuch der Analysis. Teil 1. 8. Auflage. B. G. Teubner, Stuttgart 1990, ISBN 3-519-12231-6. Satz 39.1.
4. Harro Heuser: Lehrbuch der Analysis. Teil 1. 8. Auflage. B. G. Teubner, Stuttgart 1990, ISBN 3-519-12231-6. Definition 46.1.
5. Wikibooks: Beweisarchiv: Analysis: Differentialrechnung: Differentiation der Sinusfunktion
6. H. Amann, J. Escher: Analysis I. Birkhäuser, Basel 1998, ISBN 3-7643-5974-9. S. 255.
7. G. Wittstock: Vorlesungsskript zu Analysis 1. Wintersemester 2000–2001. Definition 2.3.27.
8. Harro Heuser: Lehrbuch der Analysis. Teil 1. 8. Auflage. B. G. Teubner, Stuttgart 1990, ISBN 3-519-12231-6. Satz 38.2.
9. G. Wittstock: Vorlesungsskript zu Analysis 1. Wintersemester 2000–2001. Bemerkung 2.3.28, Punkt 1.
10. G. Wittstock: Vorlesungsskript zu Analysis 1. Wintersemester 2000–2001 Definition 2.3.2, Bemerkung 3.
11. G. Wittstock: Vorlesungsskript zu Analysis 1. Wintersemester 2000–2001. Bemerkung 2.3.28 Punkt 5.
12. N. Bourbaki: Éléments de mathématique. Topologie Générale. Springer, Berlin, ISBN 978-3-540-33936-6. Chapitre I, § 7, Définition 3.
13. N. Bourbaki: Éléments de mathématique. Topologie Générale. Springer, Berlin, ISBN 978-3-540-33936-6. Chapitre I, § 7.4.
14. N. Bourbaki: Éléments de mathématique. Topologie Générale. Springer, Berlin, ISBN 978-3-540-33936-6. Chapitre I, § 7.5.