Theoretische Informatik

Die theoretische Informatik beschäftigt sich mit der Abstraktion, Modellbildung und grundlegenden Fragestellungen, die mit der Struktur, Verarbeitung, Übertragung und Wiedergabe von Informationen in Zusammenhang stehen. Ihre Inhalte sind Automatentheorie, Theorie der formalen Sprachen, Berechenbarkeits- und Komplexitätstheorie, aber auch Logik und formale Semantik sowie die Informations-, Algorithmen- und Datenbanktheorie.

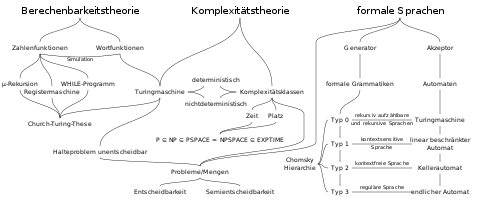
Mind-Map zu einem Teilbereich der theoretischen Informatik

Die theoretische Informatik wurde – von den Befürwortern dieser Wissenschaftskategorie – in die Strukturwissenschaften eingeordnet und bietet Grundlagen für die Definition, Verifikation und Ausführung der Programme von Programmiersprachen, den Bau der Compiler von Programmiersprachen – den Compilerbau – und die mathematische Formalisierung und Untersuchung von meist diskreten Problemstellungen und deren Modellen. Mit Hilfe mathematischer Abstraktion der Eigenschaften von gewonnenen Modellen ergaben sich nützliche Definitionen, Sätze, Beweise, Algorithmen, Anwendungen und Lösungen von bzw. zu Problemen. Die theoretische Informatik bildet mit ihren zeitlosen, mathematischen Wahrheiten und Methoden ein formales Skelett, das die Informatik in der Praxis mit konkreten Implementierungen durchdringt. Die theoretische Informatik identifizierte viele unlösbare Problemstellungen mittels der Berechenbarkeitstheorie und erlaubt, häufig mit konstruktiver Beweisführung der Komplexitätstheorie, die Abgrenzung der praktisch effizient lösbaren Probleme von denen, für die das Gegenteil gilt.

Zu den konstruktiven Methoden der theoretischen Informatik zählt auch das Entwerfen von formalen Systemen, Automaten, Graphen und Syntaxdiagrammen sowie das Festlegen von Grammatiken und Semantiken, um eine Problemstellung mit mathematischen Ausdrücken formal zu fassen und von der informellen Ebene abzuheben. Die Konstrukte beschreiben so die innere Logik eines Problems mit mathematisch-logischen Aussagen, was im Weiteren eine formale Untersuchung erlaubt und potenziell neue – durch Beweise gestützte – Aussagen und Algorithmen der formalen Modelle als Resultate erschließbar macht. Neben dem mathematischen Erkenntnisgewinn lassen sich manche der gefundenen Lösungen praktisch implementieren, um Menschen durch Maschinensemantik automatisierte Vorteile der Mathematik- und Computer-Nutzung zu verschaffen.

Geschichte der theoretischen Informatik

Die theoretische Informatik ist eng verbunden mit der Mathematik und Logik. Im 20. Jahrhundert erfolgte eine Emanzipation und Bildung als eigenständige Disziplin.

Pioniere der Disziplin waren Kurt Gödel, Alonzo Church, Alan Turing, Stephen C. Kleene, Claude Shannon, John von Neumann, Hans Hermes und Noam Chomsky.

Der Logiker Heinrich Scholz erbat (und erhielt) von Turing 1936 ein Exemplar von dessen wegweisender Arbeit On Computable Numbers, with an Application to the “Entscheidungsproblem”.[1] Auf Basis dieser Arbeit hielt Scholz (laut Achim Clausing) „das weltweit erste Seminar über Informatik“.

Automatentheorie und formale Sprachen

Die Automatentheorie definiert und formalisiert Automaten oder Rechenmaschinen und beschäftigt sich mit deren Eigenschaften und Berechnungsstärke. Unter anderem untersucht die Automatentheorie, welche Probleme von den unterschiedlichen Klassen von Rechenmaschinen gelöst werden können.

Die Theorie der formalen Sprachen betrachtet formalisierte Grammatiken und die durch diese Grammatiken erzeugten formalen Sprachen. Sie beschäftigt sich mit syntaktischen und semantischen Merkmalen dieser formalen Sprachen über einem Alphabet. Das Problem, ob ein Wort zu einer formalen Sprache gehört, wird durch Automaten gelöst; dadurch besteht ein enger Zusammenhang zwischen den Grammatiken, die formale Sprachen erzeugen, und den Automaten, die sie erkennen.

Chomsky-Hierarchie

Die meisten in der Praxis auftretenden formalen Sprachen, wie beispielsweise Programmiersprachen, besitzen eine einfache Struktur und können nach ihrer Komplexität in eine der bekannten Sprachklassen der Chomsky-Hierarchie eingeteilt werden. Die Chomsky-Hierarchie – nach Noam Chomsky, einem Pionier der Sprachtheorie – besteht aus vier Klassen. Diese sind, nach ihrer Mächtigkeit aufsteigend geordnet, die regulären Sprachen, (Typ 3), die kontextfreien Sprachen (Typ 2), die kontextsensitiven Sprachen (Typ 1) und die rekursiv aufzählbaren Sprachen (Typ 0).

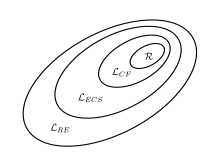
Die Sprachklassen der Chomsky-Hierarchie liegen wie folgt ineinander:
Typ 3 ⊂ Typ 2 ⊂ Typ 1 ⊂ Typ 0, hier durch die Inklusionen
R ⊂ L_CF ⊂ L_ECS ⊂ L_RE dargestellt.

Reguläre Sprachen können von endlichen Automaten,

kontextfreie Sprachen von (nichtdeterministischen) Kellerautomaten,

kontextsensitive Sprachen von linear beschränkten Turingmaschinen und

rekursiv aufzählbare Sprachen von allgemeinen Turingmaschinen erkannt werden.

Zwischen den vier Grammatikklassen und den vier Maschinenklassen der Chomsky-Hierarchie besteht eine Äquivalenz bezüglich ihrer erzeugten und erkannten Klassen von Sprachen. Die formalen Sprachen, die durch die jeweiligen Grammatikklassen der Chomsky-Hierarchie erzeugt werden, können – wie oben aufgeführt – von den entsprechenden Maschinenklassen erkannt werden und umgekehrt.

Pumping- und Jaffe-Lemmata

Bekannte praktische Hilfsmittel in der Charakterisierung von regulären und kontextfreien Sprachen sind die Pumping-Lemmata, die eine notwendige, aber nicht hinreichende Bedingung liefern, dass eine von einer Grammatik erzeugte Sprache regulär oder kontextfrei ist.[2] Auf Grund der Struktur der Aussagen der Lemmata wird das Pumping-Lemma für reguläre Sprachen auch uvw-Theorem und das Pumping-Lemma für kontextfreie Sprachen auch uvwxy-Theorem genannt. Erweiterungen wie das Lemma von Jaffe liefern im Gegensatz zu den Pumping-Lemmata ein hinreichendes Kriterium.

Beschreibung von Typ 2-Grammatiken

Die Backus-Naur-Form (nach John W. Backus und Peter Naur) oder BNF ist eine Notationskonvention für kontextfreie Grammatiken und somit für kontextfreie Sprachen. Die BNF wird in der Praxis beispielsweise dazu benutzt, die Syntaxen von Programmiersprachen zu definieren. Die jeweilige Syntax der Programmiersprachen Pascal und Modula-2 ist in der erweiterten Backus-Naur-Form, EBNF, definiert worden. Die erweiterte Backus-Naur-Form unterscheidet sich nur in einigen Notationserweiterungen von der BNF.

Berechenbarkeitstheorie

In der Berechenbarkeitstheorie wird die algorithmische Lösbarkeit von mathematischen Problemen – also deren Berechenbarkeit – untersucht. Insbesondere geht es um die Analyse der internen Struktur von Problemen und um die Klassifikation von Problemen nach verschiedenen Graden der Lösbarkeit oder deren Unlösbarkeit.

Intuitive und formale Berechenbarkeit und Churchsche These

Ausgehend von der intuitiven Berechenbarkeit, der gefühlsmäßigen Vorstellung, zu welchen Problemen sich Lösungen imaginieren und formulieren lassen, entwickelte die Berechenbarkeitstheorie eine formal mathematische Definition von Berechenbarkeit, mit der sich mathematische Beweise führen lassen, die es ermöglichen, Aussagen zur Berechenbarkeit zu verifizieren oder zu falsifizieren. Versuche, den Berechenbarkeitsbegriff formal zu fassen, führten auf die Churchsche These, die beansprucht, dass der Begriff der mathematischen Berechenbarkeit mit der Turingmaschine und gleich starken formalen Berechnungsmodellen gefunden wurde. Auf dem Fundament der mathematischen Modelle der Berechenbarkeit und der Churchschen These fußen die eigentlichen Erkenntnisse und Aussagen der Berechenbarkeitstheorie.

Unvollständigkeitssatz, Halteproblem und Satz von Rice

Mit den Methoden der Berechenbarkeitstheorie lässt sich beispielsweise auch Kurt Gödels Unvollständigkeitssatz formulieren und beweisen.[3] Ein weiteres Ergebnis der Berechenbarkeitstheorie ist die Erkenntnis, dass das Halteproblem unentscheidbar ist,[4] man also keinen Algorithmus finden kann, der beliebige Programme daraufhin untersucht, ob sie bei einer bestimmten Eingabe jemals anhalten oder nicht. Ebenfalls unentscheidbar ist nach dem Satz von Rice jedwede nicht-triviale Eigenschaft eines Programms in einer turingmächtigen Programmiersprache.[5]

Komplexitätstheorie

Die Komplexitätstheorie untersucht, welche Ressourcen (zum Beispiel Rechenzeit und Speicherplatz) in welchem Maße aufgewendet werden müssen, um bestimmte Probleme algorithmisch zu lösen. In der Regel erfolgt eine Einteilung der Probleme in Komplexitätsklassen. Die bekanntesten derartigen Klassen sind P und NP (in deutscher Literatur Notation auch in Frakturlettern: ${\mathfrak {P}}$ und ${\mathfrak {NP}}$ ). P ist die Klasse der effizient lösbaren Probleme (genauer: P ist die Klasse der Probleme, die von einer deterministischen Turingmaschine in Polynomialzeit entschieden werden können), NP die Klasse der Probleme, deren Lösungen effizient überprüft werden können (oder äquivalent: NP ist die Klasse der Probleme, die von einer nichtdeterministischen Turingmaschine in Polynomialzeit entschieden werden können).

Durch die Angabe eines Algorithmus zur Lösung eines Problems lässt sich eine Oberschranke für den oben erwähnten Bedarf an Ressourcen angeben. Die Suche nach unteren Schranken stellt sich hingegen als weitaus schwieriger dar. Hierzu muss nachgewiesen werden, dass alle möglichen Algorithmen, die nur eine bestimmte Menge von Ressourcen verwenden, ein Problem nicht lösen können.

Eine (wenn nicht sogar die) zentrale und seit Jahrzehnten offene Frage in der Komplexitätstheorie ist, ob die Klassen NP und P übereinstimmen – ein NP-vollständiges Problem in deterministischer Polynomialzeit zu lösen würde als Beweis reichen. Äquivalent dazu kann versucht werden, ein NP-vollständiges Problem auf einem Turing-äquivalenten Computer effizient zu lösen (siehe auch Churchsche These).

Die parametrisierte Algorithmik ist ein relativ junges Teilgebiet der theoretischen Informatik, in dem genauer untersucht wird, welche Instanzen von NP-vollständigen Problemen effizient zu lösen sind.

Formale Semantik

Die formale Semantik beschäftigt sich mit der Bedeutung von in einer formalen Sprache beschriebenen Programmen. Mathematisch ausgedrückt wird eine Semantikfunktion konstruiert, die ein gegebenes Programm auf die von ihm berechnete Funktion abbildet.

${\mathcal {C}}:{\mathcal {P}}\to f$

Dabei steht ${\mathcal {C}}$ für die Semantikfunktion, ${\mathcal {P}}$ für die Menge der syntaktisch korrekten Programme, $f:\subseteq \Sigma \to \Sigma$ für die von dem Programm berechnete Funktion und $\Sigma$ für die Menge der möglichen Speicherbelegungen.

Je nach mathematischem Ansatz unterscheidet man

Informationstheorie

Gegenstand der Informationstheorie ist die mathematische Beschreibung von Information. Der Informationsgehalt einer Nachricht wird durch seine Entropie charakterisiert. Damit ist es möglich, die Übertragungskapazität eines Informationskanals zu bestimmen, was die Verwandtschaft zur Kodierungstheorie begründet. Weiterhin werden informationstheoretische Methoden auch in der Kryptologie verwendet, beispielsweise ist das One-Time-Pad ein informationstheoretisch sicheres Verschlüsselungsverfahren.

Logik

Mathematische Logik wird in vielfältiger Weise in der theoretischen Informatik verwendet; dies hat umgekehrt auch zu Impulsen für die mathematische Logik geführt. Aussagenlogik und Boolesche Algebra wird z. B. für Beschreibung von Schaltkreisen verwendet; dabei kommen grundlegende Resultate der Logik wie Craig-Interpolation zum Einsatz. Zudem sind grundlegende Konzepte der Theorie der Programmierung natürlich mittels Logik ausdrückbar, neben der oben genannten Semantik vor allem im Bereich der Theorie der logischen Programmierung. Im Bereich der formalen Spezifikation werden verschiedene Logiken, u. a. Prädikatenlogik, Temporale Logik, Modallogik und dynamische Logik eingesetzt, um das intendierte Verhalten von Software- und Hardwaresystemen zu beschreiben, das dann mittels Model Checking oder Theorembeweisern verifiziert werden kann. Auch die in der künstlichen Intelligenz eingesetzten Logiken, z. B. Modallogiken, mittels derer das Wissen eines Agenten repräsentiert wird, sind Gegenstand theoretischer Untersuchungen. Für die Theorie der funktionalen Programmierung kommt die kombinatorische Logik zum Einsatz.

Weitere bedeutende Forscher

Literatur

Alexander Asteroth, Christel Baier: Theoretische Informatik. Eine Einführung in Berechenbarkeit, Komplexität und formale Sprachen. Pearson, München 2003, ISBN 3-8273-7033-7
Katrin Erk, Lutz Priese: Theoretische Informatik. Eine umfassende Einführung. 3. Auflage, Springer, Berlin 2008, ISBN 3-540-76319-8
Bernhard Heinemann, Klaus Weihrauch: Logik für Informatiker. Eine Einführung. Teubner, Stuttgart 2000, ISBN 3-519-12248-0
John E. Hopcroft, Rajeev Motwani, Jeffrey Ullman: Einführung in die Automatentheorie, formale Sprachen und Komplexitätstheorie. 2., überarb. Auflage. Pearson Studium, München 2002, ISBN 3-8273-7020-5 (Originaltitel: Introduction to automata theory, languages, and computation. Übersetzt von Sigrid Richter, Ingrid Tokar).
John Kelly: Logik im Klartext. Pearson, München 2003, ISBN 3-8273-7070-1
Uwe Schöning: Theoretische Informatik – kurzgefaßt. Spektrum Akademischer Verlag, Heidelberg 2003, ISBN 3-8274-1099-1
Christian Wagenknecht: Formale Sprachen, Abstrakte Automaten und Compiler: Lehr- und Arbeitsbuch für Grundstudium und Fortbildung. Vieweg+Teubner, 2009, ISBN 3-8348-0624-2
Ingo Wegener: Theoretische Informatik. Eine algorithmische Einführung. Teubner, Stuttgart 1999, ISBN 3-519-12123-9
Klaus W. Wagner: Einführung in die Theoretische Informatik. Grundlagen und Modelle. Springer, Berlin 1997, ISBN 3-540-58139-1
Klaus Weihrauch: Computability. Springer, Berlin 1987, ISBN 3-540-13721-1
Renate Winter: Theoretische Informatik. Grundlagen mit Übungsaufgaben und Lösungen. Oldenbourg, München 2002, ISBN 3-486-25808-7
Rolf Socher: Theoretische Grundlagen der Informatik. Hanser Verlag, München 2005, ISBN 3-446-22987-6
George M. Reed, A. W. Roscoe, R. F. Wachter: Topology and Category Theory in Computer Science. Oxford University Press 1991, ISBN 0-19-853760-3
Klaus Keimel: Domains and Processes. Springer 2001, ISBN 0-7923-7143-7
Dirk W. Hoffmann: Theoretische Informatik. 1. Auflage. Hanser Fachbuch, München 2007, ISBN 978-3-446-41511-9.

Weblinks

Hauptseite Theoretische Informatik – Seite bei Grundstudium.info

Einzelnachweise

Das Exemplar wurde am Institut für Informatik der Westfälischen Wilhelms-Universität in Münster von Achim Clausing gefunden (Westfälische Nachrichten. 28. Januar 2013: Auf den Spuren eines Pioniers: In der Unibibliothek Münster liegen Originaldrucke des Informatikers Alan Turing; online).
Uwe Schöning: Theoretische Informatik – kurzgefasst / Uwe Schöning. Spektrum, Akad. Verl., Heidelberg 2001, ISBN 3-8274-1099-1, S. 39,57.
Uwe Schöning: Theoretische Informatik – kurzgefasst / Uwe Schöning. Spektrum, Akad. Verl., Heidelberg 2001, ISBN 3-8274-1099-1, S. 149 ff.
Uwe Schöning: Theoretische Informatik – kurzgefasst / Uwe Schöning. Spektrum, Akad. Verl., Heidelberg 2001, ISBN 3-8274-1099-1, S. 127 ff.
Uwe Schöning: Theoretische Informatik – kurzgefasst / Uwe Schöning. Spektrum, Akad. Verl., Heidelberg 2001, ISBN 3-8274-1099-1, S. 130 ff.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Das Exemplar wurde am Institut für Informatik der Westfälischen Wilhelms-Universität in Münster von Achim Clausing gefunden (Westfälische Nachrichten. 28. Januar 2013: Auf den Spuren eines Pioniers: In der Unibibliothek Münster liegen Originaldrucke des Informatikers Alan Turing; online).

[2] Uwe Schöning: Theoretische Informatik – kurzgefasst / Uwe Schöning. Spektrum, Akad. Verl., Heidelberg 2001, ISBN 3-8274-1099-1, S. 39,57.

[3] Uwe Schöning: Theoretische Informatik – kurzgefasst / Uwe Schöning. Spektrum, Akad. Verl., Heidelberg 2001, ISBN 3-8274-1099-1, S. 149 ff.

[4] Uwe Schöning: Theoretische Informatik – kurzgefasst / Uwe Schöning. Spektrum, Akad. Verl., Heidelberg 2001, ISBN 3-8274-1099-1, S. 127 ff.

[5] Uwe Schöning: Theoretische Informatik – kurzgefasst / Uwe Schöning. Spektrum, Akad. Verl., Heidelberg 2001, ISBN 3-8274-1099-1, S. 130 ff.