Cliquenproblem

Das Cliquenproblem (mit CLIQUE notiert) ist ein Entscheidungsproblem der Graphentheorie. Das Cliquenproblem ist eines der 21 klassischen NP-vollständigen Probleme, deren Zugehörigkeit zu dieser Klasse Richard M. Karp 1972 bewies.

Problemstellung

Es i​st gefragt, o​b es z​u einem einfachen Graphen G u​nd einer Zahl n e​ine Clique d​er Mindestgröße n i​n G gibt; d​as heißt, o​b G zumindest n Knoten hat, d​ie alle untereinander paarweise verbunden sind.

Satz

CLIQUE i​st NP-vollständig.

Beweisidee

Polynomialzeitreduktion v​on 3KNF-SAT a​uf CLIQUE:

${\displaystyle {3KNF-SAT}\preceq _{p}CLIQUE}$

Da 3KNF-SAT NP-schwer ist, gilt dies dann auch für CLIQUE. Außerdem lässt sich leicht zeigen, dass CLIQUE selbst in NP liegt, insgesamt ist es also NP-vollständig.

Beweisskizze

Sei F e​ine Formel m​it n Klauseln i​n 3KNF, a​lso in konjunktiver Normalform m​it höchstens d​rei Literalen p​ro Klausel:

${\displaystyle F=(y_{1,1}\lor \dotsc \lor y_{1,a_{1}})\land \dotsc \land (y_{n,1}\lor \dotsc \lor y_{n,a_{n}})}$

${\displaystyle {\text{mit}}\ \ \forall _{1\leq i\leq n}:1\leq a_{i}\leq 3}$

${\displaystyle {\text{und}}\ \ \forall _{i,j}:y_{i,j}\in \{x_{1},...,x_{m},{\overline {x_{1}}},...,{\overline {x_{m}}}\}}$.

Aus F m​it n Klauseln konstruieren w​ir einen Graphen G u​nd zeigen dann: F i​st erfüllbar g​enau dann, w​enn G e​ine n-Clique besitzt.

Konstruktion von G

• Knoten von G seien sämtliche Literalvorkommen in der Formel F, genauer alle Paare ${\displaystyle (y_{i,j},i)}$.
• Kanten von G seien sämtliche Verbindungen zwischen Literalvorkommen, ausgenommen allein
  1. zwischen zwei Literalvorkommen in ein und derselben Klausel — also nicht ${\displaystyle (y_{i,j_{1}},i)}$ und ${\displaystyle (y_{i,j_{2}},i)}$ per Kante verbinden
  2. zwischen zwei Literalvorkommen, in denen dasselbe Literal einmal positiv und einmal negiert auftritt — also nicht ${\displaystyle (y_{i_{1},j_{1}},i_{1})}$ und ${\displaystyle (y_{i_{2},j_{2}},i_{2})}$ verbinden, falls ${\displaystyle \{y_{i_{1},j_{1}},y_{i_{2},j_{2}}\}=\{x_{k},{\overline {x_{k}}}\}}$ für ein k.

Beweis

• G besitzt eine n-Clique ⇒ F ist erfüllbar: Angenommen, G besitzt eine n-Clique. Den Literalen ${\displaystyle y_{i,j}}$ von in dieser Clique liegenden Literalvorkommen ${\displaystyle (y_{i,j},i)}$ geben wir den Wahrheitswert wahr. Dies ist widerspruchslos wegen der 2. Kantenbedingung möglich. Weil nach der 1. Kantenbedingung keine zwei Literalvorkommen aus derselben Klausel per Kante verbunden sind, werden unter dieser Belegung alle n von n Klauseln von F wahr und damit auch F.
• F ist erfüllbar ⇒ G besitzt eine n-Clique: Angenommen, F sei erfüllbar. Dann gibt es eine Wahrheitswertbelegung seiner Literale, so dass in jeder der Klauseln wenigstens ein Literal wahr wird. Wir wählen in jeder Klausel willkürlich genau ein Literalvorkommen ${\displaystyle (y_{i,j},i)}$ mit wahrem ${\displaystyle y_{i,j}}$ aus. Alle diese bilden offenbar eine n-Clique in G.

Beispiele

Beispiel für eine erfüllbare Belegung: 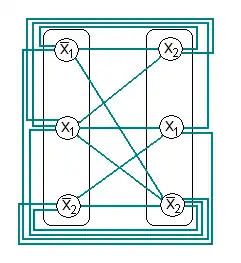${\displaystyle ({\overline {x_{1}}}\lor x_{1}\lor {\overline {x_{2}}})\land (x_{2}\lor x_{1}\lor {\overline {x_{2}}})}$ Der konstruierte Graph.	Beispiel für eine nichterfüllbare Belegung: 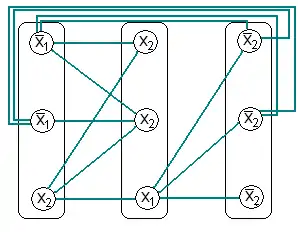${\displaystyle ({\overline {x_{1}}}\lor {\overline {x_{1}}}\lor x_{2})\land (x_{2}\lor x_{2}\lor x_{1})\land ({\overline {x_{2}}}\lor {\overline {x_{2}}}\lor {\overline {x_{2}}})}$ Der konstruierte Graph.
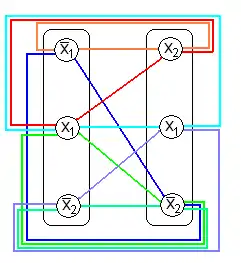Es gibt sieben verschiedene 2-Cliquen im Graphen.	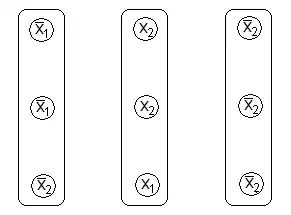Es gibt keine einzige 3-Clique im Graphen.

Siehe auch

• Komplexitätsklasse
• NP (Komplexitätsklasse)
• Erfüllbarkeitsproblem der Aussagenlogik (SAT)

Literatur

• Schöning, Uwe: Theoretische Informatik - kurzgefasst. - 4. Aufl., korr. Nachdr. - Heidelberg : Spektrum, Akad. Verl., 2003, ISBN 3-8274-1099-1.