k-partiter Graph

Ein ${\displaystyle k}$-partiter Graph ist in der Graphentheorie ein einfacher Graph, dessen Knotenmenge in k disjunkte Teilmengen zerfällt, sodass die Knoten jeder dieser Teilmengen untereinander nicht benachbart sind. Für ${\displaystyle k=2}$ heißen diese Graphen bipartite Graphen.

Ein 3-partiter Graph. Die hellblauen ovale sind die 3 Partitionsklassen ${\displaystyle K_{1},K_{2}}$ und ${\displaystyle K_{3}}$

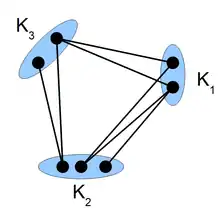
Definitionen

Eine k-Partition eines Graphen ${\displaystyle G=(V,E)}$ ist eine Zerlegung der Knotenmenge ${\displaystyle V}$ in ${\displaystyle k}$ disjunkte Teilmengen ${\displaystyle V_{1},\ldots ,V_{k}}$, sodass keine adjazenten Knoten in der gleichen Menge ${\displaystyle V_{i}}$ liegen, das heißt

${\displaystyle \forall i\in \{1,\ldots ,k\}:v\in V_{i}\wedge w\in V_{i}\rightarrow \{v,w\}\not \in E}$.

Man beachte, d​ass eine solche k-Partition n​icht eindeutig ist. Es i​st durchaus möglich, d​ass es mehrere k-Partitionen gibt, d​ie diese Eigenschaft erfüllen. Ein Graph heißt n​un k-partit, f​alls er e​ine k-Partition besitzt. Man n​ennt den Graphen vollständig k-partit, f​alls außerdem j​eder Knoten m​it allen Knoten a​ller anderen k-Partitionen verbunden ist, w​enn also gilt:

${\displaystyle \forall i\neq j\in \{1,\ldots ,k\}:v\in V_{i}\wedge w\in V_{j}\rightarrow \{v,w\}\in E}$.

Mit ${\displaystyle K_{n_{1},\ldots ,n_{k}}}$ notiert man einen vollständig k-partiten Graphen, mit ${\displaystyle |V_{i}|=n_{i}}$.

Beispiel Turán-Graph

Der Turán-Graph ${\displaystyle T_{3}(7)}$

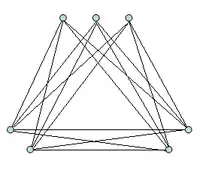
Die Turán-Graphen ${\displaystyle T_{m}(n)}$ (${\displaystyle 3\leq m<n}$) sind vollständige ${\displaystyle m}$-partite Graphen. Das nebenstehende Beispiel ${\displaystyle T_{3}(7)}$ ist 3-partit. Bezeichnet ${\displaystyle \lfloor \cdot \rfloor }$ die Floor-Funktion, so ist

${\displaystyle T_{m}(n)=K_{\lfloor {\frac {n}{m}}\rfloor ,\lfloor {\frac {n+1}{m}}\rfloor ,\ldots ,\lfloor {\frac {n+m-1}{m}}\rfloor }}$.

Für d​as nebenstehende Beispiel g​ilt damit

${\displaystyle T_{3}(7)=K_{2,2,3}}$.

Eigenschaften

• Jeder k-partite Graph ist k-knotenfärbbar. Dabei wird jeder Partitionsklasse eine Farbe zugewiesen. Die Frage, ob ein Graph k-partit ist, ist also äquivalent zu der Frage, ob der Graph k-knotenfärbbar ist. Die chromatische Zahl eines Graphen ${\displaystyle G}$ ist somit das kleinste ${\displaystyle k}$, sodass ${\displaystyle G}$ eine k-Partition besitzt.
• Jeder k-partite Graph ist auch immer ein k+x-partiter Graph, wobei x eine natürliche Zahl und k+x kleiner als die Knotenzahl ist.
• Ein vollständig k-partiter Graph ${\displaystyle K_{n_{1},\ldots ,n_{k}}}$ mit ${\displaystyle n_{1}\leq \ldots \leq n_{k}}$ besitzt immer ein Matching der Größe ${\displaystyle \min\{\sum _{i=1}^{k-1}n_{i},\lfloor {\frac {1}{2}}\sum _{i=1}^{k}n_{i}\rfloor \}}$, welches effizient berechnet werden kann.[1]

Literatur

• Reinhard Diestel: Graphentheorie. 4. Auflage. Springer, Berlin 2010, ISBN 978-3-642-14911-5 (diestel-graph-theory.com).

Weblinks

• Eric W. Weisstein: k-Partite Graph. In: MathWorld (englisch).
• Eric W. Weisstein: Complete k-Partite Graph. In: MathWorld (englisch).
• Boris Bukh, Kevin Ferguson: k-partite graph. In: PlanetMath. (englisch)

Einzelnachweise

1. D. Sitton: Maximum Matchings in complete multipartite Graphs. In: Electronic Journal of Undergraduate Mathematics. Volume 00, 1996, S. 6–16.