Clique (Graphentheorie)

Eine Clique bezeichnet in der Graphentheorie eine Teilmenge von Knoten in einem ungerichteten Graphen, bei der jedes Knotenpaar durch eine Kante verbunden ist. Zu entscheiden, ob ein Graph eine Clique einer bestimmten Mindestgröße enthält, wird Cliquenproblem genannt und gilt, wie das Finden von größten Cliquen, als algorithmisch schwierig (NP-vollständig). Das Finden einer Clique einer bestimmten Größe in einem Graphen ist ein NP-vollständiges Problem und somit auch in der Informationstechnik ein relevantes Forschungs- und Anwendungsgebiet.

Definitionen

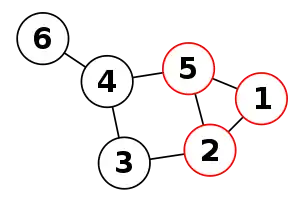
Ein Graph mit einer Clique der Größe 3.

Sei $G=(V,E)$ ein ungerichteter Graph ohne Mehrfachkanten und $U$ eine Teilmenge von $V$ . Eine Clique ist eine Teilmenge $U$ von $V$ , die einen vollständigen Teilgraphen induziert. Ist $U$ eine Clique, so gilt also für den Teilgraph $H=(U,F)$ , wobei $F$ alle Kanten aus $E$ enthält, die zwei Knoten in $U$ verbinden, dass je zwei beliebige verschiedene Knoten $v$ und $w$ aus $U$ durch eine Kante miteinander verbunden sind.

Eine Clique $U$ von $G$ nennt man maximal, wenn man keinen weiteren Knoten $v$ aus $V$ zu $U$ hinzufügen kann, so dass $U$ zusammen mit $v$ eine Clique ist. Gibt es in $G$ keine Clique, die mehr Elemente als $U$ enthält, so nennt man $U$ größte Clique. Die Anzahl der Elemente einer größten Clique nennt man Cliquenzahl.

Als Cliquenüberdeckung von $G$ der Größe $k$ bezeichnet man eine Partition der Knotenmenge $V(G)$ in $k$ paarweise disjunkte Cliquen $V_{1},V_{2},\ldots ,V_{k}$ .

Aus den Cliquen eines Graphen ergibt sich dessen Cliquen-Graph. Clique-Graphen sind für schleifenlose und ungerichtete Graphen definiert. Ein Graph ist eine Clique, wenn alle Knoten paarweise miteinander verbunden sind (Vollständiger Graph) und es keinen Knoten außerhalb der Clique gibt, der mit allen Knoten der Clique verbunden ist. Der Cliquen-Graph K(G) eines Graphen G ist der Graph, der sich ergibt, wenn alle Cliquen jeweils einem Knoten zugeordnet und zwei Knoten verbunden werden, wenn die zugehörigen Cliquen in G gemeinsame Knoten haben. Iterierte Clique-Graphen werden folgendermaßen definiert:

$K^{n}(G)=K(K^{n-1}(G)),~{\text{wenn}}~n~>~0$

$K^{n}(G)=G,~{\text{wenn}}~n~=~0$

Zwei direkt miteinander verbundene Knoten stellen dabei eine Clique der Größe 2 dar.

Gerichtete Graphen oder solche mit Mehrfachkanten sind nicht Gegenstand derartiger Betrachtungen, da es nicht auf die Richtung oder Vielfachheit der Kanten ankommt.

Eigenschaften

Zu jeder Clique eines Graphen gibt es eine stabile Menge im Komplementgraphen.

Cliquenverhalten

Wenn man Cliquen Graphen beliebig hoher Iteration betrachtet gibt es zwei mögliche Verhaltensweisen. Periodisches Cliquenverhalten tritt auf, wenn es einen Graphen gibt, der einem Graphen entspricht, der in der Abfolge von Cliquen-Graphen schon früher aufgetreten ist. Also:

$K^{i}(G)=K^{j}(G),~i\neq j$

Die zweite Möglichkeit ist, dass der Graph Cliquendivergent ist. Das ist der Fall, wenn es für die Anzahl an Knoten, aus denen ein beliebiger Graph aus der Abfolge iterierter Cliquen-Graphen besteht, keine obere Schranke gibt.

$\lim _{i\to \infty }|V(K^{i}(G))|=\infty$

V(G) ist die Menge der Knoten des Graphen G.

Zusätzlich wird der Fall unterschieden, dass die iterierten Cliquen-Graphen ab einer bestimmten Iteration gleich dem Einvertexgraph sind, ein Graph der genau aus einem Knoten besteht. In diesem Fall bezeichnet man das Cliquenverhalten als konvergent.

Die Clique-Helly-Eigenschaft

Der Hajos-Graph. Er ist der kleinste Graph, der nicht die Clique-Helly-Eigenschaft besitzt.

Ein Graph hat die Clique-Helly-Eigenschaft, wenn die Familie seiner Cliquen die Helly-Eigenschaft besitzt. Graphen mit der Clique-Helly-Eigenschaft weisen in Zusammenhang mit Clique-Graphen einige interessante Eigenschaften auf.

Die Cliquen-Graphen von Graphen mit der Clique-Helly-Eigenschaft besitzen selbst die Clique-Helly-Eigenschaft.

Zu jeden Graph H mit der Clique-Helly-Eigenschaft gibt es einen Graphen G, sodass der Clique-Graph von G isomorph zu H ist.

Der Clique-Graph der zweiten Iteration K²(G) eines Graphen G mit der Clique-Helly-Eigenschaft ist ein induzierter Subgraph von G. Ein Graph mit der Clique-Helly-Eigenschaft ist also niemals cliquendivergent und seine Periode beträgt höchstens zwei.

Probleme und Komplexität

Das Entscheidungsproblem zu einem Graphen $G$ und einer natürlichen Zahl $k$ zu entscheiden, ob $G$ eine Clique der Größe mindestens $k$ enthält, wird Cliquenproblem (CLIQUE) genannt. Das zugehörige Optimierungsproblem fragt nach der Cliquenzahl eines Graphen. Das zugehörige Suchproblem fragt nach einer größten Clique. Diese drei Probleme sind polynomiell äquivalent.

Das Cliquenproblem ist eines von Karps 21 NP-vollständigen Problemen. Die zugehörigen Optimierungs- und Suchprobleme sind NP-äquivalent. Für den Nachweis der NP-Schwere des Cliquenproblems existiert eine Reduktion von 3-SAT auf das Cliquenproblem.

Eine größte Clique lässt sich jedoch in polynomieller Zeit berechnen, wenn der Komplementgraph bipartit ist. Tatsächlich gilt sogar etwas stärker, dass die Cliquenzahl in perfekten Graphen in polynomieller Zeit berechnet werden kann. Da die chromatische Zahl und die Cliquenzahl in solchen Graphen identisch sind, ist auch ihre chromatische Zahl in polynomieller Zeit berechenbar. Die Berechnung einer maximalen Clique gelingt bereits mit einem einfachen Greedy-Algorithmus.

Software

Algorithmen zum Finden und Manipulieren von Cliquen sind in der freien Python-Bibliothek NetworkX[1] sowie in dem freien R-Paket igraph[2] implementiert.

Literatur

J. L. Szwarcfiter: A Survey on Clique Graphs. In: Recent Advances in Algorithmsand Combinatorics. Springer, New York 2003, S. 109–136.
F. Escalante: Über iterierte Clique-Graphen. In: Abhandlungen des Mathematischen Seminars der Universität Hamburg. Band 39. Springer, Berlin / Heidelberg 1973, S. 58–68.

Einzelnachweise

Algorithms – Clique. In: NetworkX 2.2 documentation. Abgerufen am 25. Oktober 2018 (englisch).
R/igraph. igraph development team, 25. Januar 2022, abgerufen am 2. Februar 2022.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Algorithms – Clique. In: NetworkX 2.2 documentation. Abgerufen am 25. Oktober 2018 (englisch).

[2] R/igraph. igraph development team, 25. Januar 2022, abgerufen am 2. Februar 2022.