Komplexitätstheorie

Die Komplexitätstheorie als Teilgebiet der theoretischen Informatik befasst sich mit der Komplexität algorithmisch behandelbarer Probleme auf verschiedenen formalen Rechnermodellen. Die Komplexität von Algorithmen wird in deren Ressourcenverbrauch gemessen, meist Rechenzeit oder Speicherplatzbedarf, manchmal auch speziellere Maße wie die Größe eines Schaltkreises oder die Anzahl benötigter Prozessoren bei parallelen Algorithmen. Die Komplexität eines Problems ist wiederum die Komplexität desjenigen Algorithmus, der das Problem mit dem geringstmöglichen Ressourcenverbrauch löst.

Die Komplexitätstheorie unterscheidet sich von der Berechenbarkeitstheorie, die sich mit der Frage beschäftigt, welche Probleme prinzipiell algorithmisch gelöst werden können. Demgegenüber besteht das wichtigste Forschungsziel der Komplexitätstheorie darin, die Menge aller lösbaren Probleme zu klassifizieren. Insbesondere versucht man, die Menge der effizient lösbaren Probleme, deren Ressourcenverbrauch in der Praxis bewältigt werden kann, von der Menge der inhärent schwierigen Probleme abzugrenzen.

Einordnung in die Theoretische Informatik

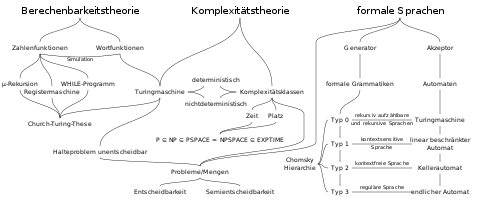
Die Komplexitätstheorie innerhalb der theoretischen Informatik

Die Komplexitätstheorie gilt, neben der Berechenbarkeitstheorie und der Theorie der Formalen Sprachen, als einer der drei Hauptbereiche der Theoretischen Informatik. Zu ihren wesentlichen Forschungszielen gehört die Klassifizierung von Problemen im Hinblick auf den zu ihrer Lösung notwendigen Aufwand. Eine besondere Rolle spielt dabei die Abgrenzung der praktisch effizient lösbaren Probleme. Die Komplexitätstheorie grenzt daher diejenigen Probleme ein, zu denen andere Disziplinen der Informatik überhaupt sinnvollerweise nach effizienten Lösungen suchen sollten, und motiviert so die Entwicklung praxistauglicher Approximationsalgorithmen.

Neben dem reinen Erkenntnisgewinn bereichert auch das Methodenarsenal der komplexitätstheoretischen Forschung zahlreiche angrenzende Gebiete. So führt etwa ihre enge Verzahnung mit der Automatentheorie zu neuen Maschinenmodellen und einem umfassenderen Verständnis der Arbeitsweise von Automaten. Die häufig konstruktive Beweisführung findet auch im Rahmen des Entwurfs und der Analyse von Algorithmen und Datenstrukturen Anwendung.

Probleme aus Sicht der Komplexitätstheorie

Entscheidungsprobleme als formale Sprachen

Entscheidungsproblem

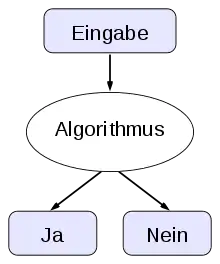
Den zentralen Gegenstand der Komplexitätstheorie bilden Probleme, und zwar in der Regel Entscheidungsprobleme, deren Instanzen eine Ja/Nein-Antwort erfordern. Ein Entscheidungsproblem wird dabei oft als formale Sprache dargestellt. Man drückt jede Probleminstanz als Wort über einem Alphabet aus, d. h. als Folge von Zeichen aus diesem Alphabet. Die fragliche Sprache besteht aus den Wörtern, denen eine Instanz mit der Antwort „Ja“ entspricht. Die Aufgabe besteht dann in der Lösung des Wortproblems, also darin, für ein gegebenes Wort zu entscheiden, ob es zu der Sprache gehört oder nicht, und damit hat man auch die Antwort auf die entsprechende Probleminstanz gefunden.

Wenn zum Beispiel das Problem darin besteht zu entscheiden, ob ein Graph zusammenhängend ist oder nicht, dann wäre ein Wort eine Darstellung eines beliebigen Graphen. Die zugehörige zu entscheidende Sprache wäre die Menge der Wörter, die einen zusammenhängenden Graphen darstellen.

Man könnte annehmen, dass die Einschränkung auf Entscheidungsprobleme viele wichtige Probleme ausschließt. Es gibt jedoch zu allen im Sinne der Komplexitätstheorie relevanten Problemen auch ein entsprechendes Entscheidungsproblem. Betrachtet man zum Beispiel das Problem der Multiplikation zweier Zahlen, so besteht die dazugehörige Sprache des Entscheidungsproblems aus allen Zahlen-Tripeln $(a,b,c)$ , für die der Zusammenhang $a\cdot b=c$ gilt. Die Entscheidung, ob ein gegebenes Tripel zu dieser Sprache gehört, entspricht dem Lösen des Problems der Multiplikation zweier Zahlen.

Berechnungsprobleme als Abbildungen

Neben Entscheidungsproblemen betrachtet man auch Berechnungsprobleme. Ein solches erfordert eine Antwort, die die Problemlösung beschreibt. Das Multiplikationsproblem beispielsweise stellt sich in der Praxis meist als Berechnungsproblem: Man will das Produkt zweier Zahlen ermitteln.

Man versteht ein Berechnungsproblem also als eine Abbildung aus einem Definitionsbereich in einen Lösungsraum, im Fall der Multiplikation von natürlichen Zahlen also als Abbildung $\mathbb {N} \times \mathbb {N} \rightarrow \mathbb {N$ . Ein anderes Beispiel ist das Problem des Handlungsreisenden. Hier sucht man nach der optimalen Reihenfolge, in der man gegebene Orte besucht, wobei die Gesamtlänge der Route minimal sein soll. Viele Optimierungsprobleme sind von großer praktischer Bedeutung. Für die Definition der meisten Komplexitätsklassen wird jedoch die Formulierung durch Entscheidungsprobleme bevorzugt.

Eine wichtige Unterkategorie der Berechnungsprobleme stellen die Optimierungsprobleme dar. Bei Optimierungsproblemen besteht der funktionale Zusammenhang aus der Forderung, das Maximum bzw. Minimum einer gegebenen Kostenfunktion über alle möglichen Lösungen des Problems zu bestimmen. Beim Problem des Handlungsreisenden wäre also die Länge der optimalen Route zu berechnen.

Probleminstanzen

Eine Probleminstanz ist nicht mit dem Problem selbst zu verwechseln. Ein Problem stellt in der Komplexitätstheorie eine allgemeine Fragestellung, eine Schablone, dar. Eine Instanz des Problems ist dann eine vollständige Fragestellung, welche die richtige Antwort (ja bzw. nein im Fall eines Entscheidungsproblems) festlegt.

Eine Instanz des Problems des Handlungsreisenden könnte zum Beispiel die Frage sein, ob eine Route durch die Landeshauptstädte Deutschlands mit einer maximalen Länge von 2000 km existiert. Die Entscheidung über diese Route hat jedoch nur begrenzten Wert für andere Probleminstanzen, wie etwa eine Rundreise durch die Sehenswürdigkeiten Mailands. In der Komplexitätstheorie interessiert man sich daher für Aussagen, die unabhängig von konkreten Instanzen sind.

Ein Problem wird so allgemein formuliert, dass es eine unendliche Menge von Probleminstanzen definiert, denn es ist nicht sinnvoll, nach der Komplexität einer endlichen Menge von Instanzen zu fragen; ein Programm könnte eine Liste von vorgefertigten Antworten enthalten und nur durch Tabellenzugriff die richtige Lösung ausgeben, was den Aufwand für die Ermittlung der Antworten nicht widerspiegelt. Interessant wird es erst, wenn eine unendliche Menge von Instanzen gegeben ist und man einen Algorithmus finden will, der für jede Instanz die richtige Antwort berechnet.

Problemrepräsentationen

Als formale Sprachen werden Probleme und deren Instanzen über abstrakten Alphabeten definiert. Häufig wird das binäre Alphabet mit den Symbolen 0 und 1 gewählt, da dies der Verwendung von Bits bei modernen Rechnern am nächsten kommt. Eingaben werden dann durch Alphabetsymbole kodiert. An Stelle von mathematischen Objekten wie Graphen verwendet man möglicherweise eine Bitfolge, die der Adjazenzmatrix des Graphen entspricht, an Stelle von natürlichen Zahlen zum Beispiel deren Binärdarstellung.

Auch wenn sich Beweise komplexitätstheoretischer Aussagen in der Regel konkreter Repräsentationen der Eingabe bedienen, versucht man Aussagen und Betrachtung unabhängig von Repräsentationen zu halten. Dies kann etwa erreicht werden, indem man sicherstellt, dass die gewählte Repräsentation bei Bedarf ohne allzu großen Aufwand in eine andere Repräsentation transformiert werden kann, ohne dass sich hierdurch die Berechnungsaufwände insgesamt signifikant verändern. Um dies zu ermöglichen, ist unter anderem die Auswahl eines geeigneten universellen Maschinenmodells von Bedeutung.

Problemgröße

Hat man ein Problem formal definiert (zum Beispiel das Problem des Handlungsreisenden in Form eines Graphen mit Kantengewichten), so möchte man Aussagen darüber treffen, wie sich ein Algorithmus bei der Berechnung der Problemlösung in Abhängigkeit von der Schwierigkeit des Problems verhält. Im Allgemeinen sind bei der Beurteilung der Schwierigkeit des Problems viele verschiedene Aspekte zu betrachten. Dennoch gelingt es häufig, wenige skalare Größen zu finden, die das Verhalten des Algorithmus im Hinblick auf den Ressourcenverbrauch maßgeblich beeinflussen. Diese Größen bezeichnet man als die Problemgröße. In aller Regel entspricht diese der Eingabelänge (bei einer konkret gewählten Repräsentation der Eingabe).

Man untersucht nun das Verhalten des Algorithmus in Abhängigkeit von der Problemgröße. Die Komplexitätstheorie interessiert sich für die Frage: Wie viel Mehrarbeit ist für wachsende Problemgrößen notwendig? Steigt der Aufwand (in Relation zur Problemgröße) zum Beispiel linear, polynomial, exponentiell oder gar überexponentiell?

So kann man beim Problem des Handlungsreisenden die Problemgröße als Anzahl der vorgegebenen Orte definieren (wobei man vernachlässigt, dass auch die vorgegebenen Streckenlängen verschieden große Eingabegrößen aufweisen können). Dann ist dieses Problem für die Problemgröße 2 trivial, da es hier überhaupt nur eine mögliche Lösung gibt und diese folglich auch optimal sein muss. Mit zunehmender Problemgröße wird ein Algorithmus jedoch mehr Arbeit leisten müssen.

Bester, schlechtester und durchschnittlicher Fall für Problemgrößen

Auch innerhalb einer Problemgröße lassen sich verschiedene Verhaltensweisen von Algorithmen beobachten. So hat das Problem des Handlungsreisenden für die 16 deutschen Landeshauptstädte dieselbe Problemgröße $n=16$ wie das Finden einer Route durch 16 europäische Hauptstädte. Es ist keineswegs zu erwarten, dass ein Algorithmus unter den unterschiedlichen Bedingungen (selbst bei gleicher Problemgröße) jeweils gleich gut arbeitet. Da es jedoch in der Regel unendlich viele Instanzen gleicher Größe für ein Problem gibt, gruppiert man diese zumeist grob in drei Gruppen: bester, durchschnittlicher und schlechtester Fall. Diese stehen für die Fragen:

Bester Fall: Wie arbeitet der Algorithmus (in Bezug auf die in Frage stehende Ressource) im günstigsten Fall?
Durchschnittlicher Fall: Wie arbeitet der Algorithmus durchschnittlich (wobei die zugrundegelegte Verteilung für die Berechnung eines Durchschnitts nicht immer offensichtlich ist)?
Amortisierter Fall: Wie arbeitet der Algorithmus im schlechtesten Fall bei einer Folge von Durchläufen?
Schlechtester Fall: Wie arbeitet der Algorithmus im schlimmsten Fall?

Die Funktionen in den Ergebnissen zu den Fragen sind, wenn sie scharf angegeben sind, aufsteigend geordnet, d. h.: ein Problem, das amortisiert bspw. quadratischen Bedarf hat, hat (höchstens) quadratischen Bedarf auch im Durchschnitt und im schlechtesten Fall keinen geringeren.

Untere und obere Schranken für Probleme

Die Betrachtung bester, schlechtester und durchschnittlicher Fälle bezieht sich stets auf eine feste Eingabelänge. Auch wenn die Betrachtung konkreter Eingabelängen in der Praxis von großem Interesse sein kann, ist diese Sichtweise für die Komplexitätstheorie meist nicht abstrakt genug. Welche Eingabelänge als groß oder praktisch relevant gilt, kann sich aufgrund technischer Entwicklungen sehr schnell ändern. Es ist daher gerechtfertigt, das Verhalten von Algorithmen in Bezug auf ein Problem gänzlich unabhängig von konkreten Eingabelängen zu untersuchen. Man betrachtet hierzu das Verhalten der Algorithmen für immer größer werdende, potentiell unendlich große Eingabelängen. Man spricht vom asymptotischen Verhalten des jeweiligen Algorithmus.

Bei dieser Untersuchung des asymptotischen Ressourcenverbrauchs spielen untere und obere Schranken eine zentrale Rolle. Man möchte also wissen, welche Ressourcen für die Entscheidung eines Problems mindestens und höchstens benötigt werden. Für die Komplexitätstheorie sind die unteren Schranken von besonderem Interesse: Man möchte zeigen, dass ein bestimmtes Problem mindestens einen bestimmten Ressourcenverbrauch beansprucht und es folglich keinen Algorithmus geben kann, der das Problem mit geringeren Ressourcen entscheidet. Solche Ergebnisse helfen, Probleme nachhaltig bezüglich ihrer Schwierigkeit zu separieren. Jedoch sind bisher nur vergleichsweise wenige aussagekräftige untere Schranken bekannt. Der Grund hierfür liegt in der Problematik, dass sich Untersuchungen unterer Schranken stets auf alle denkbaren Algorithmen für ein Problem beziehen müssen; also auch auf Algorithmen, die heute noch gar nicht bekannt sind.

Im Gegensatz dazu gelingt der Nachweis oberer Schranken in der Regel durch die Analyse konkreter Algorithmen. Durch den Beweis der Existenz auch nur eines Algorithmus, der die obere Schranke einhält, ist der Nachweis bereits erbracht.

Bei bestimmten Problemen, etwa der Komplexität von Verschlüsselungsverfahren, wird der Nachweis versucht, dass der zu erwartende Ressourcenverbrauch beim Versuch, das Verfahren zu brechen, jedes realistische Maß übersteigt. Für Probleme, die selbst mit einem Computer von der Größe der Erde nicht während der Lebensdauer der Erde zu lösen sind, wurde der Begriff transcomputationales Problem geprägt.

Maschinenmodelle in der Komplexitätstheorie

Kostenfunktionen

Zur Analyse des Ressourcenverbrauchs von Algorithmen sind geeignete Kostenfunktionen zu definieren, welche eine Zuordnung der Arbeitsschritte des Algorithmus zu den verbrauchten Ressourcen ermöglichen. Um dies tun zu können, muss zunächst festgelegt werden, welche Art von Arbeitsschritt einem Algorithmus überhaupt erlaubt ist. Diese Festlegung erfolgt in der Komplexitätstheorie über abstrakte Maschinenmodelle – würde man auf reale Rechnermodelle zurückgreifen, so wären die gewonnenen Erkenntnisse bereits in wenigen Jahren überholt. Der Arbeitsschritt eines Algorithmus erfolgt in Form einer Befehlsausführung auf einer bestimmten Maschine. Die Befehle, die eine Maschine ausführen kann, sind dabei durch das jeweilige Modell streng limitiert. Darüber hinaus unterscheiden sich verschiedene Modelle etwa in der Handhabung des Speichers und in ihren Fähigkeiten zur parallelen Verarbeitung, d. h. der gleichzeitigen Ausführung mehrerer Befehle. Die Definition der Kostenfunktion erfolgt nun durch eine Zuordnung von Kostenwerten zu den jeweils erlaubten Befehlen.

Kostenmaße

Häufig wird von unterschiedlichen Kosten für unterschiedliche Befehle abstrahiert und als Kostenwert für eine Befehlsausführung immer 1 gesetzt. Sind auf einer Maschine beispielsweise Addition und Multiplikation die erlaubten Operationen, so zählt man für jede Addition und jede Multiplikation, die im Laufe des Algorithmus berechnet werden müssen, den Kostenwert von 1 hinzu. Man spricht dann auch von einem uniformen Kostenmaß. Ein solches Vorgehen ist dann gerechtfertigt, wenn sich die erlaubten Operationen nicht gravierend unterscheiden und wenn der Wertebereich, auf dem die Operationen arbeiten, nur eingeschränkt groß ist. Dies wird schon für eine einfache Operation wie die Multiplikation klar: Das Produkt zweier einstelliger Dezimalzahlen dürfte sich ungleich schneller errechnen lassen als das Produkt zweier hundertstelliger Dezimalzahlen. Bei einem uniformen Kostenmaß würden beide Operationen dennoch mit einem Kostenwert von 1 veranschlagt. Sollten sich die möglichen Operanden im Laufe eines Algorithmus tatsächlich so gravierend unterscheiden, so muss ein realistischeres Kostenmaß gewählt werden. Häufig wählt man dann das logarithmische Kostenmaß. Der Bezug auf den Logarithmus ergibt sich daraus, dass sich eine Dezimalzahl $n$ im Wesentlichen durch $\log _{2}(n)$ viele Binärziffern darstellen lässt. Man wählt zur Repräsentation der Operanden Binärziffern aus und definiert die erlaubten booleschen Operationen. Sollte das jeweilige Maschinenmodell Adressen verwenden, so werden auch diese binär codiert. Auf diese Weise werden die Kosten über die Länge der Binärdarstellung logarithmisch gewichtet. Andere Kostenmaße sind möglich, werden jedoch nur selten eingesetzt.

Maschinenmodelle und Probleme

Man unterscheidet verschiedene Berechnungsparadigmen: der pragmatischste Typ ist sicher der der deterministischen Maschinen; weiterhin gibt es den in der Theorie besonders relevanten Typ der nichtdeterministischen Maschinen; weiterhin gibt es noch probabilistische Maschinen, alternierende und andere. In der Regel kann man jedes Maschinenmodell mit jedem der obigen Paradigmen definieren. Einige Paradigmen, so zum Beispiel der Nichtdeterminismus, modellieren dabei einen Typ, der der Theorie vorbehalten bleiben muss, da man den Nichtdeterminismus in der dort definierten Form physikalisch nicht bauen kann, (sie „erraten“ einen richtigen Pfad in einem Berechnungsbaum), lassen sich jedoch häufig leicht zu einem gegebenen Problem konstruieren. Da eine Transformation von nichtdeterministischen in deterministische Maschinen immer relativ einfach möglich ist, konstruiert man daher zunächst eine nichtdeterministische Maschinenversion und transformiert diese später in eine deterministische.

Daraus geht eine wichtige Beweistechnik der Komplexitätstheorie hervor: Lässt sich zu einem gegebenen Problem ein bestimmter Maschinentyp konstruieren, auf dem das Problem mit bestimmten Kosten entschieden werden kann, so kann damit bereits die Komplexität des Problems eingeschätzt werden. Tatsächlich werden sogar die unterschiedlichen Maschinenmodelle bei der Definition von Komplexitätsklassen zugrundegelegt. Dies entspricht einer Abstraktion von einem konkreten Algorithmus: Wenn ein Problem auf Maschine $M$ entscheidbar ist (wobei ein entsprechender Algorithmus evtl. noch gar nicht bekannt ist), so lässt es sich unmittelbar einer bestimmten Komplexitätsklasse zuordnen, nämlich derjenigen, die von $M$ definiert wird. Dieses Verhältnis zwischen Problemen und Maschinenmodellen ermöglicht Beweisführungen ohne die umständliche Analyse von Algorithmen.

Häufig eingesetzte Maschinenmodelle

Besonders häufig eingesetzte Modelle sind:

Zur Untersuchung parallelisierbarer Probleme können darüber hinaus auch parallelisierte Versionen dieser Maschinen zum Einsatz kommen, insbesondere die parallele Registermaschine.

Die erweiterte Church-Turing-These

Für die Verwendung von Maschinenmodellen in der Komplexitätstheorie ist eine Erweiterung der Church-Turing-These von Bedeutung, die auch als erweiterte Church-Turing-These bezeichnet wird. Sie besagt, dass alle universellen Maschinenmodelle in Bezug auf die Rechenzeit bis auf polynomielle Faktoren gleich mächtig sind. Dies ermöglicht dem Komplexitätstheoretiker eine relativ freie Wahl des Maschinenmodells im Hinblick auf das jeweilige Untersuchungsziel. Auch diese These ist nicht beweisbar; im Gegensatz zur gewöhnlichen Church-Turing-These wäre es aber möglich, sie durch ein Gegenbeispiel zu widerlegen.

Modellmodifikationen für Speicherplatzanalysen

Zur Untersuchung des Mindestspeicherbedarfs, der für die Lösung von Problemen benötigt wird, nimmt man häufig die folgenden Modifikationen des verwendeten Maschinenmodells (in der Regel eine Turingmaschine) vor:

Der Eingabespeicher darf nur gelesen werden.
Auf die Ausgabe darf nur geschrieben werden. Der Schreibkopf wird nur nach Schreibvorgängen und immer in dieselbe Richtung bewegt (falls das Maschinenmodell eine solche Bewegung vorsieht).

Für die Untersuchung des Speicherbedarfs dürfen dann Ein- und Ausgabe der Maschine unberücksichtigt bleiben. Die Motivation für diese Änderungen ist die folgende: Würde zum Beispiel der Eingabespeicher in die Speicherplatzanalyse einbezogen, so könnte kein Problem in weniger als ${\mathcal {O}}(n)$ Platzbedarf gelöst werden, denn das Eingabewort hat ja immer genau die Länge und damit den Speicherbedarf n. Indem man die Eingabe nur lesbar macht, verhindert man, dass sie für Zwischenrechnungen verwendet werden kann. Man kann dann die Eingabe bei der Berechnung des Platzbedarfs vernachlässigen. Eine ähnliche Argumentation führt zu der Einschränkung der Ausgabe. Durch die zusätzliche Einschränkung einer möglichen Kopfbewegung wird verhindert, dass die Kopfposition verwendet wird, um sich Information zu „merken“. Insgesamt stellen all diese Einschränkungen sicher, dass Ein- und Ausgabe bei der Speicherplatzanalyse nicht berücksichtigt werden müssen.

Die vorgenommenen Modifikationen beeinflussen das Zeitverhalten der Maschine übrigens nur um einen konstanten Faktor und sind damit vernachlässigbar.

Landau-Notation

Bei der Untersuchung von Größenordnungen für Aufwände wird in der Komplexitätstheorie ausgiebig von der Landau- oder O-Notation Gebrauch gemacht, um den (minimalen, mittleren oder maximalen) Zeit- oder Speicherplatzbedarf eines Algorithmus zu beschreiben. Man spricht dann von Zeitkomplexität bzw. Platzkomplexität. Die Komplexität kann vom verwendeten Maschinenmodell abhängen. In der Regel nimmt man jedoch ein „normales“ Modell an, zum Beispiel ein der Turingmaschine äquivalentes. Dabei werden lineare Faktoren und Konstanten aus der Betrachtung ausgeblendet. Diese Vorgehensweise mag zunächst überraschen, wäre doch für den Praktiker häufig bereits eine Halbierung der Aufwände von hoher Bedeutung.

Der Standpunkt der Komplexitätstheorie lässt sich theoretisch mit einer Technik rechtfertigen, die man als lineares Beschleunigen oder auch Speedup-Theorem bezeichnet. (Wir beschränken uns hier auf das Zeitverhalten. Analoge Beweise kann man auch für den Speicherbedarf oder andere Ressourcen führen.) Das Speedup-Theorem besagt vereinfachend, dass sich zu jeder Turingmaschine, die ein Problem in Zeit $T$ entscheidet, eine neue Turingmaschine konstruieren lässt, die das Problem in Zeit weniger als $\varepsilon \cdot T$ entscheidet. Dabei kann $\varepsilon >0$ beliebig klein gewählt sein. Das bedeutet nichts anderes, als dass sich jede Turingmaschine, die ein bestimmtes Problem löst, um einen beliebigen konstanten Faktor beschleunigen lässt. Der Preis für diese Beschleunigung besteht in einer stark vergrößerten Arbeitsalphabetgröße und Zustandsmenge der verwendeten Turingmaschine (letztlich also „Hardware“).

Diese Beschleunigung wird unabhängig von der Problemgröße erreicht. Bei der Betrachtung des asymptotischen Verhaltens von Problemen ergibt es daher keinen Sinn, konstante Faktoren zu berücksichtigen – solche Faktoren ließen sich durch Anwendung der Beschleunigungstechnik wieder beseitigen. Die Vernachlässigung konstanter Faktoren, die sich in der O-Notation ausdrückt, hat daher nicht nur praktische Gründe, sie vermeidet auch Verfälschungen im Rahmen komplexitätstheoretischer Betrachtungen.

Oft ist es sehr aufwendig oder ganz unmöglich, für ein Problem $L$ eine Funktion $f_{L}\colon w\rightarrow f_{L}(w)$ anzugeben, die allgemein jeder beliebigen Eingabe für ein Problem die zugehörige Anzahl der Rechenschritte (bzw. der Speicherzellen) zuordnet. Daher begnügt man sich in der Regel damit, statt jede Eingabe einzeln zu erfassen, sich lediglich auf die Eingabelänge $n=|w|$ zu beschränken. Es ist aber meist ebenfalls zu aufwendig, eine Funktion $f_{L}\colon n\rightarrow f_{L}(n),n=|w|$ anzugeben.

Daher hat man die Landau-Notation entwickelt, die sich auf das asymptotische Verhalten der Funktion $f_{L}$ beschränkt. Man betrachtet also, in welchen Schranken sich der Rechenaufwand (der Bedarf an Speicher und Rechenzeit) hält, wenn man die Eingabe vergrößert. Das wichtigste Landau-Symbol ist ${\mathcal {O}}$ (großer lateinischer Buchstabe „O“), mit dem man obere Schranken angeben kann; untere Schranken sind im Allgemeinen viel schwieriger zu finden. Dabei bedeutet $f\in {\mathcal {O}}(g)$ (oft auch $f(n)={\mathcal {O}}(g(n))$ ), dass eine Konstante $c>0$ und ein $n_{0}\in \mathbb {N}$ existieren, so dass für alle $n>n_{0}$ gilt: $f(n)\leq c\cdot g(n)$ . In anderen Worten: Für alle Eingabelängen ist der Rechenaufwand $f(n)$ nicht wesentlich größer – d. h. höchstens um einen konstanten Faktor $c$ – als $g(n)$ .

Dabei ist die Funktion $f$ nicht immer bekannt; als Funktion $g$ wird hingegen meist eine Funktion gewählt, deren Wachstum gut bekannt ist (wie $g(x)=x^{2}$ oder $g(x)=2^{x}$ ). Die Landau-Notation ist gerade dazu da, den Rechenaufwand (Platzbedarf) abzuschätzen, wenn es zu aufwendig ist, die genaue Funktion anzugeben, bzw. wenn diese zu kompliziert ist.

Die Landau-Symbole erlauben es dadurch, Probleme und Algorithmen nach ihrer Komplexität in Komplexitätsklassen zusammenzufassen.

In der Komplexitätstheorie lassen sich die verschiedenen Probleme und Algorithmen dann folgendermaßen vergleichen: Man kann für Problemstellungen mit $\Omega$ eine untere Schranke für beispielsweise die asymptotische Laufzeit angeben, mit ${\mathcal {O}}$ entsprechend eine obere Schranke. Bei ${\mathcal {O}}(f)$ wird die Form von $f$ (z. B. $f(n)=n^{2}$ ) auch als die Komplexitätsklasse oder Aufwandsmaß bezeichnet (also z. B. quadratisch).

Bei dieser Notation werden, wie die Definitionen der Landau-Symbole zeigen, konstante Faktoren vernachlässigt. Dies ist gerechtfertigt, da die Konstanten zu großen Teilen vom verwendeten Maschinenmodell bzw. bei implementierten Algorithmen von der Qualität des Compilers und diversen Eigenschaften der Hardware des ausführenden Computer abhängig sind. Damit ist ihre Aussagekraft über die Komplexität des Algorithmus sehr beschränkt.

Bildung von Komplexitätsklassen

Eine wesentliche Aufgabe der Komplexitätstheorie besteht darin, sinnvolle Komplexitätsklassen festzulegen, in diese die vorliegenden Probleme einzusortieren und Aussagen über die wechselseitigen Beziehungen zwischen den Klassen zu finden.

Einflussgrößen bei der Bildung von Komplexitätsklassen

Eine Reihe von Faktoren nehmen Einfluss auf die Bildung von Komplexitätsklassen. Die wichtigsten sind die folgenden:

Das zugrunde liegende Berechnungsmodell (Turingmaschine, Registermaschine usw.).
Der verwendete Berechnungsmodus (deterministisch, nichtdeterministisch, probabilistisch usw.).
Die betrachtete Berechnungsressource (Zeit, Platz, Prozessoren usw.).
Das angenommene Kostenmaß (uniform, logarithmisch).
Die eingesetzte Schrankenfunktion.

Anforderungen an Schrankenfunktionen

Zur Angabe oder Definition von Komplexitätsklassen verwendet man Schrankenfunktionen. Schreibt man beispielsweise DTIME(f), so meint man damit die Klasse aller Probleme, die auf einer deterministischen Turingmaschine in der Zeit ${\mathcal {O}}(f)$ entschieden werden können. $f$ ist dabei eine Schrankenfunktion. Um als Schrankenfunktion für komplexitätstheoretische Analysen eingesetzt werden zu können, sollte die Funktion mindestens die folgenden Anforderungen erfüllen:

$f\colon \mathbb {N} \rightarrow \mathbb {N}$ (Schrittzahl, Speicher usw. werden als natürliche Zahlen berechnet).
$f(n+1)\geq f(n)$ (monotones Wachstum).
Die Funktion $f$ muss selbst in Zeit ${\mathcal {O}}(f)$ und mit Raum ${\mathcal {O}}(f)$ berechenbar sein. (Raum-/Zeitkonstruierbarkeit)

Eine Funktion, die diesen Anforderungen genügt, bezeichnet man auch als echte Komplexitätsfunktion. Der Sinn der Anforderungen ist zum Teil technischer Natur. Die Schrankenfunktion kann selbst auf konstruktive Art (zum Beispiel als Turingmaschine) in Beweise einfließen und sollte sich daher für diese Zwecke „gutartig“ verhalten. An dieser Stelle soll nur darauf hingewiesen werden, dass bei der Wahl der Schrankenfunktion eine gewisse Vorsicht walten muss, weil sonst bestimmte algorithmische Techniken nicht angewandt werden können.

Die meisten in der Praxis auftretenden Funktionen entsprechen den oben genannten Einschränkungen, so etwa die konstante Funktion, die Logarithmusfunktion, die Wurzelfunktion, Polynome, die Exponentialfunktion sowie alle Kombinationen dieser Funktionen. Es folgt eine Übersicht der wichtigsten Schrankenfunktionen mit der jeweils üblichen Sprechweise. Die Angabe erfolgt wie üblich in O-Notation.

Die wichtigsten Schrankenfunktionen

konstant	${\mathcal {O}}(1)$
logarithmisch	${\mathcal {O}}(\log n)$
polylogarithmisch	${\mathcal {O}}(\log ^{k}n)$ für $k\geq 1$
linear	${\mathcal {O}}(n)$
linearithmisch	${\mathcal {O}}(n\log n)$
quadratisch	${\mathcal {O}}(n^{2})$
polynomial	${\mathcal {O}}(n^{k})$ für $k\geq 1$
exponentiell	${\mathcal {O}}(d^{n})$ für $d>1$
faktoriell	${\mathcal {O}}(n!)$

Hierarchiesätze

Für die gebildeten Klassen möchte man möglichst beweisen, dass durch zusätzlich bereitgestellte Ressourcen tatsächlich mehr Probleme gelöst werden können. Diese Beweise bezeichnet man als Hierarchiesätze (auch Separationssätze genannt), da sie auf den Klassen der jeweiligen Ressource eine Hierarchie induzieren. Es gibt also Klassen, die in eine echte Teilmengenbeziehung gesetzt werden können. Wenn man solche echten Teilmengenbeziehungen ermittelt hat, lassen sich auch Aussagen darüber treffen, wie groß die Erhöhung einer Ressource sein muss, um damit eine größere Zahl von Problemen berechnen zu können. Von besonderem Interesse sind dabei wiederum die Ressourcen Zeit und Raum. Die induzierten Hierarchien bezeichnet man auch als Zeithierarchie und Raumhierarchie.

Die Hierarchiesätze bilden letztlich das Fundament für die Separierung von Komplexitätsklassen. Sie bilden einige der frühesten Ergebnisse der Komplexitätstheorie. Es muss ergänzt werden, dass alle Hierarchiesätze auf diversen Voraussetzungen beruhen. Eine dieser Voraussetzungen ist etwa, dass die oben genannten Anforderungen an echte Komplexitätsfunktionen erfüllt werden. Ohne die Einhaltung dieser Anforderungen bricht tatsächlich die gesamte Klassenhierarchie in sich zusammen.[1]

Zeithierarchiesatz

Der Zeithierarchiesatz besagt:

\operatorname {DTIME} {\big (}f(n){\big )}\subsetneq \operatorname {DTIME} {\big (}f(n)\cdot \log ^{2}(f(n)){\big )}

Es gibt also Probleme, deren asymptotischer Zeitbedarf auf einer deterministischen Turingmaschine innerhalb der Klasse $\operatorname {DTIME} {\big (}f(n)\cdot \log ^{2}(f(n)){\big )},$ aber nicht in $\operatorname {DTIME} {\big (}f(n){\big )}$ liegt. Eine ähnliche Beziehung lässt sich für nichtdeterministische Turingmaschinen finden.

Raumhierarchiesatz

Der Raumhierarchiesatz besagt:

\operatorname {DSPACE} {\big (}f(n){\big )}\subsetneq \operatorname {DSPACE} {\big (}f(n)\cdot \log(f(n)){\big )}

Die Aussage ist analog zum Zeithierarchiesatz. Man erkennt jedoch, dass im Vergleich zur Zeit bereits eine geringere Steigerung des Raumes ausreicht (Faktor $\log(f(n))$ im Vergleich zu $\log ^{2}(f(n))$ ), um eine größere Klasse zu bilden. Dies entspricht auch einer intuitiven Erwartung, verhält sich doch der Raum insgesamt aufgrund seiner Wiederverwendbarkeit (alte Zwischenergebnisse können überschrieben werden) gutmütiger.

Wofür die Hierarchiesätze nicht gelten

Die Hierarchiesätze beziehen sich ausschließlich auf den jeweils gleichen Berechnungsmodus und eine einzelne Ressource, also zum Beispiel auf die Ressource Zeit auf einem deterministischen Maschinenmodell. Es wird jedoch keine Aussage darüber getroffen, wie sich etwa Raum- und Zeitklassen zueinander verhalten oder in welchem Verhältnis deterministische oder nichtdeterministische Klassen zueinander stehen. Dennoch gibt es derartige Zusammenhänge. Sie werden in den Abschnitten Beziehungen zwischen Raum- und Zeitklassen und Beziehungen zwischen deterministischen und nichtdeterministischen Klassen behandelt.

Wichtige Zeitklassen

DTIME(f): Allgemeine Schreibweise für deterministische Zeitklassen.
P: Deterministisch in Polynomialzeit entscheidbare Sprachen.
EXPTIME: Deterministisch in Exponentialzeit entscheidbare Sprachen.
NTIME(f): Allgemeine Schreibweise für nichtdeterministische Zeitklassen.
NP: Nichtdeterministisch in Polynomialzeit entscheidbare Sprachen.
NEXPTIME: Nichtdeterministisch in Exponentialzeit entscheidbare Sprachen.
NC: Parallel in polylogarithmischer Zeit berechenbare Funktionen.

Wichtige Raumklassen

DSPACE(f): Allgemeine Schreibweise für deterministische Raumklassen.
L: Deterministisch mit logarithmisch beschränktem Raum entscheidbare Sprachen.
PSPACE: Deterministisch mit polynomial beschränktem Raum entscheidbare Sprachen.
NSPACE(f): Allgemeine Schreibweise für nichtdeterministische Raumklassen.
NL: Nichtdeterministisch mit logarithmisch beschränktem Raum entscheidbare Sprachen.
CSL: Kontextsensitive Sprachen sind die nichtdeterministisch mit linear beschränktem Raum entscheidbaren Sprachen.

Siehe auch: Liste von Komplexitätsklassen

Komplementbildungen

Für jede Komplexitätsklasse K lässt sich ihre Komplementklasse CoK bilden: Die Komplementklasse enthält genau die Komplemente der Elemente der ursprünglichen Klasse. Fasst man K als Menge von Sprachen auf ( $K\subseteq {\mathcal {P}}(\Sigma ^{*})$ , siehe Potenzmenge), so ist die Komplementklasse $CoK=\{L\,\mid \,\Sigma ^{*}\setminus L\in K\}$ . Bezogen auf die entsprechenden Entscheidungsprobleme heißt das: CoK enthält die Probleme, auf deren Instanzen die Antwort immer gegensätzlich lautet wie bei einem Problem in K.

Im Gegensatz dazu kann man auch das Komplement einer Klasse K betrachten. Dieses enthält genau die Sprachen/Probleme aus einer gegebenen Grundmenge, die nicht in K sind; diese Probleme sind in der Regel viel schwerer als die in K. Die Komplementklasse CoK hingegen besitzt mit K in der Regel einen nichtleeren Durchschnitt.

Für deterministische Maschinen gilt in der Regel K = CoK, da in der Übergangsfunktion einfach nur die Übergänge zu akzeptierenden Zuständen durch Übergänge zu verwerfenden Zuständen ausgetauscht werden müssen und umgekehrt. Für andere Berechnungsmodi gilt dies jedoch nicht, da hier die Akzeptanz anders definiert ist. Beispielsweise ist bislang unbekannt, ob NP = CoNP gilt. P = CoP ist wahr, da das zugrunde liegende Modell deterministisch ist und hier die akzeptierenden und ablehnenden Zustände in den Berechnungen einfach ausgetauscht werden können, wie im vorherigen Absatz angesprochen. So sehen wir sofort, dass P im Durchschnitt von NP und CoNP enthalten ist. Ob dieser Durchschnitt genau P ist, ist nicht bekannt.

Das P-NP-Problem und seine Bedeutung

Eines der wichtigsten und nach wie vor ungelösten Probleme der Komplexitätstheorie ist das P-NP-Problem. Ist die Klasse P gleich der Klasse NP? Diese Frage kann als eine zentrale Forschungsmotivation der Komplexitätstheorie angesehen werden, und eine Vielzahl der komplexitätstheoretischen Ergebnisse wurde erzielt, um der Lösung des P-NP-Problems näher zu kommen.

Die Klasse P: Praktisch lösbare Probleme

Die Tragweite des P-NP-Problems resultiert aus der Erfahrung, dass die Probleme der Klasse P in der Regel praktisch lösbar sind: Es existieren Algorithmen, um Lösungen für diese Probleme effizient oder doch mit vertretbarem zeitlichem Aufwand zu berechnen. Der zeitliche Aufwand zur Problemlösung wächst für die Probleme der Klasse P maximal polynomial. In der Regel lassen sich Algorithmen finden, deren Zeitfunktionen Polynome niedrigen Grades sind. Da das gewählte Maschinenmodell dieser Zeitklasse deterministisch (und damit realisierbar) ist, entsprechen die Probleme der Klasse P in etwa den praktisch lösbaren Problemen, auch wenn Instanzen erheblicher Größe betrachtet werden.

Die Klasse NP: Effizient verifizierbare Probleme

Die Algorithmen zur Lösung der Probleme in NP basieren auf einem nichtdeterministischen Maschinenmodell. Für solche Maschinen wird eine unbeschränkte Parallelisierbarkeit der sich verzweigenden Berechnungspfade angenommen, die technisch nicht realisiert werden kann. Zwar arbeiten auch die Algorithmen zur Lösung der Probleme in NP in polynomialer Zeit, aber eben auf der Basis eines physikalisch nicht realisierbaren Maschinenmodells.

Alternativ zur Definition über den Nichtdeterminismus kann man die Klasse NP auch über die Verifikation von Problemen beschreiben. Ein Verifikationsalgorithmus bekommt neben der eigentlichen Eingabe zusätzlich einen Zeugen (auch Zertifikat genannt) übergeben. Für eine Ja-Instanz muss der Verifikationsalgorithmus zumindest bei einem möglichen Zeugen zu einer positiven Antwort kommen. Bei einer Nein-Instanz darf der Verifikationsalgorithmus für keinen Zeugen zu einer positiven Antwort kommen. Gibt es für ein Problem einen Verifikationsalgorithmus, der mit einem Zeugen polynomieller Länge in polynomieller Zeit arbeitet, dann liegt dieses Problem in der Klasse NP. Ein Beispiel für einen effizient verifizierbares Problem ist das Erfüllbarkeitsproblem (SAT). Hier wird gefragt ob es für eine boolesche Formel eine Belegung ihrer Variablen gibt, sodass die Formel wahr ist. Ein möglicher Verifikationsalgorithmus benutzt als Zeugen einen Vektor, welcher die Variablenbelegung kodiert. Für eine gegebene Variablenbelegung ist es leicht, einen effizienten Algorithmus zu entwerfen, der die Formel für diese Belegung auswertet. Damit ist dieses Problem in der Klasse NP. Das Finden der Belegung ist nicht Aufgabe des Verifikationsalgorithmus.

Eine nichtdeterministische Turingmaschine kann ein Problem in NP dadurch lösen, dass sie erst alle möglichen Lösungen erzeugt, wobei der Rechenweg in entsprechend viele Pfade verzweigt wird, und anschließend jede dieser Lösungen verifiziert, was deterministisch, also ohne weitere Verzweigung, erfolgen kann.

Es gibt Probleme in NP, die für große Instanzen als praktisch unlösbar gelten. Dazu gehören die NP-vollständigen Probleme. In dieser Klasse finden sich Probleme aus fast allen Bereichen der Informatik. Aber nicht alle Probleme in NP sind schwer, weil NP auch die Klasse P enthält.

Der Fall P = NP

Würde das P-NP-Problem im Sinne von P = NP gelöst, so wüssten wir, dass es selbst für NP-vollständige Probleme Algorithmen geben muss, die mit polynomiellem Zeitaufwand arbeiten.

Da umgekehrt die Definition der NP-Vollständigkeit Algorithmen voraussetzt, mit denen es gelingt, beliebige Probleme aus NP in polynomieller Zeit auf NP-vollständige Probleme zu reduzieren, wären mit der polynomialen Lösbarkeit auch nur eines einzigen NP-vollständigen Problems sofort sämtliche Probleme der Klasse NP in polynomieller Zeit lösbar. Dies hätte eine Problemlösekraft in der gesamten Informatik zur Folge, wie sie auch durch noch so große Fortschritte in der Hardware-Entwicklung nicht erreicht werden kann.

Andererseits ist für bestimmte Anwendungsfälle eine Lösung des P-NP-Problems im Sinne von P = NP eher unerwünscht. Beispielsweise würden asymmetrische Verschlüsselungsverfahren erheblich an Sicherheit verlieren, da diese dann in Polynomialzeit gebrochen werden könnten.

Der Fall P ≠ NP

Würde das P-NP-Problem im Sinne von P ≠ NP gelöst, so wäre klar, dass weitere Bemühungen, polynomielle Lösungen für NP-vollständige Probleme zu finden, sinnlos wären. Man kann sich leicht vorstellen, dass aufgrund der hohen Bedeutung der Probleme in NP die Bemühungen um eine effiziente Lösung erst dann eingestellt werden, wenn diese nachgewiesenermaßen unmöglich ist. Bis zu diesem Zeitpunkt wird noch viel private und öffentliche Forschungsenergie aufgewandt werden.

In vielen Theoremen wird heute jedoch angenommen, dass P ≠ NP gilt, denn nur so kann ohne einen Beweis der Gleichheit trotzdem effektive Forschungsarbeit geleistet werden. Man sucht nach Auswegen durch Approximationen und Heuristiken, nach Problemeinschränkungen, die die Praxis nicht vernachlässigen.

Konsequenzen für die Komplexitätstheorie

Zu den wichtigsten Forschungszielen der Komplexitätstheorie gehört die Abgrenzung des praktisch Machbaren und damit des Betätigungsfeldes der Informatik schlechthin. Die vorherigen Abschnitte haben die Wichtigkeit dieser Grenzziehung verdeutlicht. Im Zuge der Versuche, das P-NP-Problem zu lösen, hat die Komplexitätstheorie zahlreiche Ergebnisse zu Tage gefördert und ihre Analysemethoden Zug um Zug verfeinert. Diese Ergebnisse werden insbesondere beim Entwurf und der Analyse praktisch wichtiger Algorithmen angewandt und wirken so auch unmittelbar auf die Praktische Informatik.

Die seit über dreißig Jahren andauernden Bemühungen, das P-NP-Problem zu lösen, gewähren darüber hinaus dem praktischen Informatiker ein großes Maß an Sicherheit, dass isolierte Bemühungen zur effizienten Lösung von Problemen aus NP mehr oder weniger sinnlos sind. Die praktische Informatik konzentriert sich daher bei der Lösung für Probleme aus NP auf Näherungslösungen oder die Abwandlung der ursprünglichen Probleme. So kann sich beispielsweise die Problemkomplexität von Optimierungs-Algorithmen enorm verringern, wenn man keine optimale Lösung anstrebt, sondern mit einer fast optimalen Lösung zufrieden ist. Die Komplexitätstheorie liefert für diese Vorgehensweise die theoretische Rückendeckung.

Sprachen und Komplexitätsklassen

Das folgende Inklusionsdiagramm gibt einen – recht groben – Überblick über die Zusammenhänge zwischen Klassen der Berechenbarkeitstheorie, der Chomsky-Hierarchie und den bedeutendsten Komplexitätsklassen.

Inklusionsdiagramm

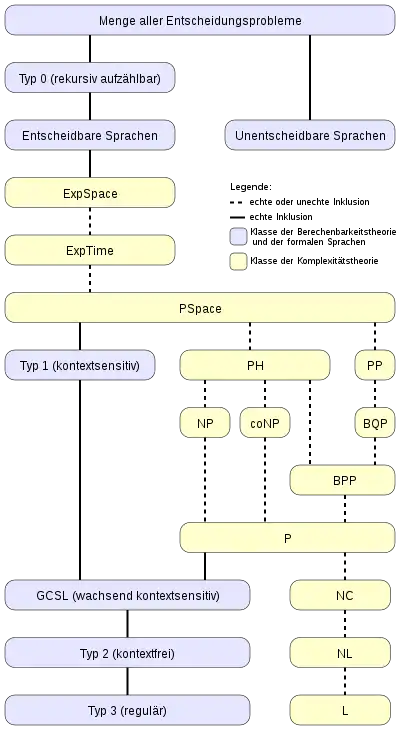
Geschichte der Komplexitätstheorie

Nachdem in den vorhergehenden Abschnitten zahlreiche Grundbegriffe und wichtige Ergebnisse der Komplexitätstheorie erläutert wurden, wird in den folgenden Abschnitten ein geschichtlicher Abriss gegeben, der die zeitliche Abfolge dieser Ergebnisse einordnen helfen soll.

Grundlagen

Vor dem eigentlichen Beginn der explizit auf die Komplexität von Algorithmen bezogenen Forschung wurden zahlreiche Grundlagen erarbeitet. Als wichtigste kann dabei die Konstruktion der Turingmaschine durch Alan Turing im Jahr 1936 angesehen werden, die sich für spätere Algorithmen-Analysen als ausgesprochen flexibles Modell erwies.

Als erste informelle komplexitätstheoretische Untersuchungen werden Ergebnisse von John Myhill (1960), Raymond Smullyan (1961) und Hisao Yamada (1962) angesehen, die sich mit speziellen raum- und zeitbeschränkten Problemklassen beschäftigt haben, jedoch in ihren Arbeiten noch keinen Ansatz zu einer allgemeinen Theorie entwickelten.

Beginn der komplexitätstheoretischen Forschung

Einen ersten großen Schritt in Richtung einer solchen Theorie unternehmen Juris Hartmanis und Richard E. Stearns in ihrer 1965 erschienenen Arbeit On the computational complexity of algorithms. Sie geben bereits eine quantitative Definition von Zeit- und Platzkomplexität und wählen damit bereits die beiden Ressourcen aus, die bis heute als die wichtigsten angesehen werden. Dabei wählen sie die Mehrband-Turingmaschine als Grundlage und treffen damit eine sehr robuste Entscheidung, die in vielen komplexitätstheoretischen Feldern Bestand hat. Sie erarbeiten auch bereits erste Hierarchiesätze.

In den folgenden Jahren kommt es zu einer Reihe fundamentaler Ergebnisse. 1967 veröffentlichte Manuel Blum das Speedup-Theorem. 1969 folgt das Union-Theorem von Edward M. McCreight und Albert R. Meyer. Und 1972 veröffentlicht Allan Borodin das Gap-Theorem. Diese Ergebnisse lassen sich nicht nur als grundlegend für die Komplexitätstheorie ansehen, sie stellen auch ein Abtasten des noch neuen Forschungsgebietes dar, das sich zugleich noch durch möglichst „spektakuläre“ Ergebnisse rechtfertigen muss. So treffen diese Theoreme z. T. zwar überraschende Aussagen, sind aber mitunter auf Annahmen gebaut, die man heute einschränken würde. Beispielsweise werden keine echten Komplexitätsfunktionen (siehe oben) vorausgesetzt.

In derselben Zeit, die etwa die ersten zehn Jahre komplexitätstheoretischer Forschung umfasst, kommt es zur Formulierung der Klasse P als der Klasse der „praktisch lösbaren“ Probleme. Alan Cobham zeigt, dass die Polynomialzeit robust unter der Wahl des Maschinenmodells ist (was man heute unter der erweiterten Church-Turing These zusammenfasst). Darüber hinaus erweisen sich viele mathematische Funktionen als in Polynomialzeit berechenbar.

Erforschung der Klasse NP

Die Klasse NP tritt zuerst bei Jack Edmonds auf den Plan, der jedoch zunächst nur eine informelle Definition gibt. Die Tatsache, dass zahlreiche wichtige Probleme in NP zu liegen scheinen, lässt diese Klasse jedoch bald als attraktives Forschungsfeld erscheinen. Der Begriff der Reduzierbarkeit und die darauf basierende NP-Vollständigkeit wird entwickelt und findet zuerst im Satz von Cook (1971) prägnanten Ausdruck: Das Erfüllbarkeitsproblem (SAT) ist NP-vollständig und damit ein schwerstes Problem in NP. Nebenbei bemerkt bezog sich die ursprüngliche Arbeit von Stephen Cook auf Tautologien (aussagenlogische Formeln, die durch jede Belegung erfüllt werden), während der Begriff der Erfüllbarkeit nicht erwähnt wird. Da die Ergebnisse bezüglich der Tautologien jedoch relativ einfach auf die Erfüllbarkeit übertragen werden können, rechnet man sie Stephen Cook zu. Einen Teil dieser Übertragung leistet Richard Karp (1972), indem er die Technik der Reduktion ausarbeitet. Völlig unabhängig von diesen Arbeiten entwickelte Leonid Levin (1973) in der damaligen Sowjetunion eine Theorie der NP-Vollständigkeit, die im Westen für lange Zeit unbeachtet blieb.

1979 veröffentlichten Michael R. Garey und David S. Johnson ein Buch, welches 300 NP-vollständige Probleme beschreibt (Computers and intractability). Dieses Buch wurde für künftige Forscher zu einer wichtigen Referenz.

Randomisierte Komplexitätsklassen

1982 stellt Andrew Yao das Konzept der Falltürfunktionen (trapdoor functions) vor, die eine spezielle Art von Einwegfunktionen (one way functions) darstellen, und zeigt deren grundlegende Wichtigkeit in der Kryptographie auf. Jedoch genügt für die Schwierigkeit, einen Code zu knacken, die Worst-Case-Betrachtungsweise der Komplexitätsklassen wie NP nicht. Es dürfen vielmehr auch keine Algorithmen existieren, die diese Probleme in einem signifikanten Anteil aller Fälle effizient lösen. Dies korrespondiert zum Modell der probabilistischen Turingmaschine und motiviert die Einführung randomisierter Komplexitätsklassen wie ZPP, RP oder BPP (alle eingeführt von John T. Gill, 1977).

Mit dieser Übersicht wurden die wesentlichen Grundsteine der Geschichte der Komplexitätstheorie gelegt. Wie in anderen Forschungsgebieten auch, fächern sich die neueren Ergebnisse in viele, teils sehr spezielle Teilbereiche auf.

Literatur

Sanjeev Arora & Boaz Barak: Computational Complexity. A Modern Approach. Cambridge University Press, Cambridge 2009, ISBN 978-0-521-42426-4.
Ding-Zhu Du & Ker-I Ko: Theory of Computational Complexity. John Wiley & Sons, New York 2000, ISBN 0-471-34506-7.
Lance Fortnow & Steve Homer: A Short History of Computational Complexity. 14. November 2002 (PDF, 225 kB)
Michael R. Garey & David S. Johnson: Computers and Intractability: A guide to the theory of NP-completeness. Freeman, New York 2003, ISBN 0-7167-1045-5.
Juris Hartmanis & Richard E. Stearns: On the computational complexity of algorithms. In: Transactions of the American Mathematical Society. Vol. 117, 1965, S. 285–306 (PDF; 2018 KB)
Jan van Leeuwen (Hrsg.): Handbook of Theoretical Computer Science, Volume A: Algorithms and Complexity. The MIT Press/Elsevier, Amsterdam 1994, ISBN 0-262-72020-5.
Christos Papadimitriou: Computational Complexity. Addison-Wesley, Reading/Mass. 1995, ISBN 0-201-53082-1.
K. Rüdiger Reischuk: Komplexitätstheorie – Band I: Grundlagen: Maschinenmodelle, Zeit- und Platzkomplexität, Nichtdeterminismus. 2. Auflage. Teubner, Stuttgart/Leipzig 1999, ISBN 3-519-12275-8.
Michael Sipser: Introduction to the Theory of Computation. 2. Auflage. Thomson, Boston 2006, ISBN 0-534-95097-3. (International Edition)
Ingo Wegener: Komplexitätstheorie. Grenzen der Effizienz von Algorithmen. 1. Auflage. Springer, Berlin 2003, ISBN 3-540-00161-1.

Weblinks

Commons: Komplexitätstheorie – Sammlung von Bildern, Videos und Audiodateien

Complexity Zoo – Verzeichnis der wichtigsten Komplexitätsklassen

Fußnoten

Derartige Probleme gibt es beispielsweise im Bereich der probabilistischen Komplexitätsklassen. Schränkt man hier – wie für praktisch verwendbare probabilistische Algorithmen erforderlich – die Fehlerwahrscheinlichkeit ein, so resultiert daraus unter anderem, dass die Komplexitätsklassen nicht mehr aufzählbar sind. Dies ist aber für alle Separationsverfahren eine Voraussetzung. Als Ergebnis lassen sich Polynomzeitalgorithmen plötzlich durch Linearzeitalgorithmen ersetzen. Das Beispiel zeigt, wie sensibel das Geflecht aus Voraussetzungen und den abgeleiteten Sätzen insgesamt ist.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Derartige Probleme gibt es beispielsweise im Bereich der probabilistischen Komplexitätsklassen. Schränkt man hier – wie für praktisch verwendbare probabilistische Algorithmen erforderlich – die Fehlerwahrscheinlichkeit ein, so resultiert daraus unter anderem, dass die Komplexitätsklassen nicht mehr aufzählbar sind. Dies ist aber für alle Separationsverfahren eine Voraussetzung. Als Ergebnis lassen sich Polynomzeitalgorithmen plötzlich durch Linearzeitalgorithmen ersetzen. Das Beispiel zeigt, wie sensibel das Geflecht aus Voraussetzungen und den abgeleiteten Sätzen insgesamt ist.