Entmischung (Thermodynamik)

Als Entmischung oder Phasenseparation bezeichnet man in der Thermodynamik einen in Gemischen aus kondensierter Materie auftretenden Phasenübergang, in dessen Verlauf aus einer homogenen Mischphase koexistierende Phasen unterschiedlicher stofflicher Zusammensetzung entstehen.[1] Die ursprünglich vorhandene homogene Mischphase und die aus dieser entstandenen koexistierenden Phasen weisen dabei denselben Aggregatzustand auf.

Thermodynamische Grundlagen

Darstellung in Phasendiagrammen

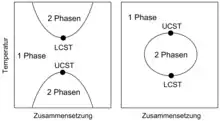
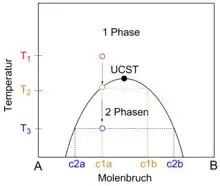
Beispiele für Zusammensetzungs-Temperatur-Phasendiagramme binärer Mischungen mit Binodalen (schwarze Kurven). LCST steht für untere kritische Lösungstemperatur (lower critical solution temperature), UCST für obere kritische Lösungstemperatur (upper critical solution temperature).

Zusammensetzungs-Temperatur-Phasendiagramm einer binären Mischung. Wird von Zustand T₁/c1a aus die Temperatur verringert, wird bei Zustand T₂/c1a die Binodale überschritten und das Koexistenzgebiet erreicht. Bei T₃ liegen koexistierende Phasen mit den Zusammensetzungen c2a und c2b vor.

Gemische können sowohl als homogene Mischphase als auch in Form koexistierender Phasen vorliegen. Der Zustandsraum eines Gemisches kann eine oder mehrere Mischungslücken enthalten. Eine Mischungslücke ist ein Koexistenzgebiet aus Zuständen, in denen das Gemisch in Form koexistierender Phasen vorliegt. Eine als Binodale bezeichnete Kurve trennt die Mischungslücke von Zuständen, in denen das Gemisch als homogene Mischphase vorliegt. Eine Entmischung findet statt, wenn das Gemisch von einem Zustand, in dem es als homogene Mischphase stabil ist, durch Überschreiten einer Binodale im Verlauf einer Zustandsänderung in einen Zustand innerhalb einer Mischungslücke überführt wird. Eine derartige Zustandsänderung kann durch Änderung einer Zustandsgröße der Gemisches, wie etwa des Druckes, der Temperatur $T$ oder des Volumens, ausgelöst werden. Auch eine Änderung der stofflichen Zusammensetzung der Mischphase, etwa durch Verdunstung eines Lösungsmittels, kann Entmischung induzieren. Umgekehrt bildet sich aus koexistierenden Phasen eine homogene Mischphase, wenn das Gemisch von einem Zustand innerhalb einer Mischungslücke in einen Zustand überführt wird, in dem das System als homogene Mischphase stabil ist. Nimmt das Gemisch einen Zustand in einer Mischungslücke ein, zerfällt es in koexistierende Phasen, die auf der Binodalen liegenden Zuständen entsprechen. Die Verbindungslinie zwischen den koexistierenden Zuständen wird als Konode bezeichnet. Die Extrema der Binodalen stellen kritische Punkte dar, an denen die Zusammensetzungen der koexistierenden Phasen und der homogenen Mischphase ununterscheidbar werden. Die zu den Extrema gehörenden Temperaturen sind die kritischen Mischungstemperaturen. Für binäre Gemische wird die Binodale häufig mit Hilfe von Phasendiagrammen dargestellt, in denen entlang der x-Achse die Systemzusammensetzung in Form des Stoffmengenanteils einer der Komponenten als Zustandsgröße, in der sich die koexistierenden Phasen unterscheiden, aufgetragen wird. Entlang der y-Achse wird eine intensive Zustandsgröße, wie beispielsweise der Druck oder die Temperatur, aufgetragen, die in den im thermodynamischen Gleichgewicht stehenden koexistierenden Phasen den gleichen Wert haben muss.[2] Im Falle ternärer Gemische lässt sich die Binodale in ein Dreiecksdiagramm projizieren, welches die Zusammensetzung des ternären Gemisches darstellt.[3]

Binodalen und Spinodalen

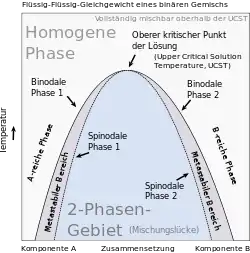
Das thermodynamische Gleichgewicht von Gemischen wird in der Regel durch den für das Gemisch erreichbaren minimal möglichen Wert der freien Enthalpie definiert, die hier als thermodynamisches Potential fungiert. Trägt man für eine Temperatur, bei der das Gemisch eine Mischungslücke aufweist, dessen freie Enthalpie als Funktion der Gemisch-Zusammensetzung auf, besitzt die so erhaltene Kurve zwei Minima. Befindet sich die Zusammensetzung des Gemisches außerhalb des von den Minima eingeschlossenen Bereiches, tritt keine Entmischung ein, und das Gemisch ist als homogene Mischphase stabil. Im von den beiden Minima eingeschlossenen Zusammensetzungsbereich zerfällt die homogene Mischphase hingegen in koexistierende Phasen mit den durch die Position der Minima vorgegebenen Zusammensetzungen. Die Minima entsprechen daher den im Gleichgewicht stehenden koexistierenden Zuständen des phasenseparierten Gemisches. Diese liegen auf der Binodale und sind durch eine Konode verbunden. Die freie Enthalpie als Funktion der Gemisch-Zusammensetzung weist im von den beiden Minima eingeschlossenen Zusammensetzungsbereich ein Maximum auf. Zwischen jedem der Minima und dem zwischen diesen lokalisierten Maximum weist die Kurve jeweils einen Wendepunkt auf. Im Temperatur-Zusammensetzungs-Phasendiagramm definieren diese Wendepunkte eine als Spinodale bezeichnete Kurve innerhalb der Mischungslücke.

Nähert man die Temperatur einer kritischen Temperatur des Gemisches an, nähern sich auch die Zusammensetzungen der koexistierenden Phasen an, so dass die Minima der freien Enthalpie als Funktion der Gemisch-Zusammensetzung immer weiter zusammenrücken. Dementsprechend wird auch die Spinodale immer enger. Am kritischen Punkt vereinigen sich die Minima zu einem einzigen Minimum. Entsprechend weist die freie Enthalpie außerhalb einer Mischungslücke maximal ein Minimum auf. Weiterhin hat die Spinodale am kritischen Punkt einen Extremwert und fällt dort mit der Binodalen zusammen.[4][5]

Freie Mischungsenthalpie

Mischungs- und Entmischungsprozesse sind als Zustandsänderung wegunabhängig, so dass Entmischungsprozesse auch durch Zustandsgrößen beschrieben werden können, die sich auf die entsprechenden, umgekehrt ablaufenden Mischungsprozesse beziehen. Die freie Mischungsenthalpie $\Delta G_{\text{mix}}$ eines Gemisches ist gemäß der bekannten Legendre-Transformation der Gibbs-Helmholtz-Gleichung wie folgt von der Mischungsenthalpie $\Delta H_{\text{mix}}$ und der Mischungsentropie $\Delta S_{\text{mix}}$ abhängig:

\Delta G_{\text{mix}}=\Delta H_{\text{mix}}-T\cdot \Delta S_{\text{mix}}

Im Falle von Polymerlösungen und Polymerblends wird die freie Mischungsenthalpie durch das Flory-Huggins-Modell vorhergesagt.

Mechanismen von Entmischungsprozessen

Binodale (äußere Kurve) und Spinodale (innere Kurve) in einem Zusammensetzungs-Temperatur-Phasendiagramm. Innerhalb der grauen Fläche findet binodale, innerhalb der blauen Fläche spinodale Entmischung statt.

Binodale Entmischung

Überführt man ein Gemisch von einem Zustand, in dem eine homogene Mischphase stabil ist, in einen Zustand, der sich innerhalb einer Mischungslücke im durch Binodale und Spinodale begrenzten Bereich befindet, wird das homogene Gemisch metastabil. Zusammensetzungsfluktuationen, die eine hohe Amplitude, jedoch eine geringe Wellenlänge aufweisen, können zur Ausbildung von Keimen einer neuen Phase in der metastabilen Matrixphase führen. Sofern die so gebildeten Keime die kritische Keimgröße überschreiten, werden diese stabil und wachsen durch Ostwald-Reifung. Die auch als Nukleation bezeichnete Keimbildung erfolgt in der Regel sporadisch, da die Ausbildung stabiler Keime zunächst endergon ist und eine freie Enthalpie-Barriere überwunden werden muss. Daher bilden sich nach dem Überführen des Gemisches in die Mischungslücke im Durchschnitt eine bestimmte Anzahl Keime pro Zeitintervall. Da zu einem bestimmten Zeitpunkt nach der Zustandsänderung die einzelnen Keime der sich neu bildenden Phase unterschiedliche Wachstumsdauern aufweisen, sind transiente Entmischungsmorphologien[6] durch sphärische Domänen[6] der sich neu bildenden Phase mit einer breiten Größenverteilung gekennzeichnet. Die zeitliche Evolution eines binodal entmischenden Gemisches lässt sich durch die Johnson-Mehl-Avrami-Kolmogorow-Gleichung modellieren. Grundlegende Arbeiten zur binodalen Entmischung stammen von Josiah Willard Gibbs[7][8] sowie von John W. Cahn und John E. Hilliard.[9] Weitere Arbeiten zu binodaler Entmischung wurden unter anderem im Hinblick auf polymerhaltige Gemische durchgeführt.[10][11][12]

Spinodale Entmischung

Evolution einer spinodalen Entmischung und der mit dieser gekoppelten Aufrauung der Entmischungsmorphologie gemäß der Cahn–Hilliard-Gleichung.

Durchlichtmikroskopische Aufnahmen charakteristischer Entmischungsmorphologien von Blends aus Poly(vinylpyrrolidon) und Poly-D,L-lactid. A) Massenverhältnis 1:5, binodale Entmischung; B) Massenverhältnis 5:1, spinodale Entmischung.

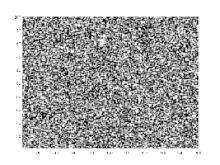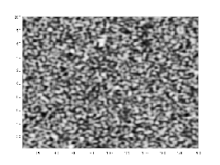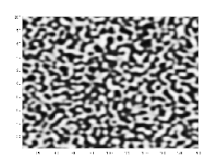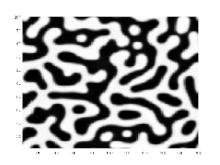
Wird ein Gemisch von einem Zustand, in dem es als homogene Mischphase stabil ist, durch eine Zustandsänderung in denjenigen Bereich einer Mischungslücke überführt, der sich innerhalb der Spinodalen befindet, wird das homogene Gemisch instabil gegenüber Fluktuationen seiner Dichte oder Zusammensetzung, selbst wenn die Amplituden der Fluktuationen infinitesimal sind. Das Gemisch entmischt sich daher spontan in einem exergonen Prozess, ohne dass eine freie Enthalpie-Barriere zu überwinden ist. Derartige spontane Entmischungsprozesse, die mittels der Cahn-Hilliard-Gleichung beschrieben werden[13][14] und deren theoretische Beschreibung maßgeblich auf John W. Cahn zurückgeht,[15][16] bezeichnet man als spinodale Entmischung.[1] Diese führt, sofern sich die Volumenanteile der entstehenden koexistierenden Phasen nicht allzu sehr unterscheiden, zur Ausbildung einer bikontinuierlichen Entmischungsmorphologie, in der die koexistierenden Phasen zwei sich gegenseitig interpenetrierende Netzwerke ausbilden. Die ursprünglich hohe innere Grenzfläche zwischen den koexistierenden Phasen verringert sich im weiteren Verlauf durch Aufrauung (englisch: coarsening) der Entmischungsmorphologie mittels Ostwald-Reifung. In sehr späten Stadien kann die bikontinuierliche Entmischungsmorphologie aufbrechen, so dass diskrete Domänen einer Minoritätsphase in einer Matrixphase erhalten werden. Wenn der Volumenanteil einer Minoritätsphase deutlich unter dem Volumenanteil einer Matrixphase liegt, bildet die Minoritätsphase zu keinem Zeitpunkt ein kontinuierliches Netzwerk aus, sondern liegt in Form diskreter Domänen vor. Da spinodale Entmischung auf das Wachstum periodischer Zusammensetzungsfluktuationen zurückgeht, sind spinodale Entmischungsmorphologien regelmäßiger als Entmischungsmorphologien, die aus binodalen Entmischungen resultieren.[17][18][19][20] Fourier-Spektren mikroskopischer Bilder von spinodalen Enmischungsmorphologien weisen typischerweise ein Halo auf.

Entmischung an Grenzflächen und in begrenzenden Geometrien

Entmischungsprozesse, die in der Nähe von Grenzflächen stattfinden, werden vom Benetzungsverhalten der Komponenten eines separierenden Gemisches beeinflusst. Sowohl im Einphasengebiet als auch im Koexistenzgebiet eines Gemisches wird dessen örtliche Zusammensetzung in der Nähe einer Grenzfläche durch Wechselwirkungen mit dieser beeinflusst. Im Einphasengebiet kann sich eine Komponente des Gemisches an der Grenzfläche anreichern oder sogar eine kontinuierliche Benetzungsschicht ausbilden. Der Übergang zwischen beiden Szenarien wird als prewetting transition bezeichnet.[21] Andererseits wird eine Grenzfläche in Kontakt mit einem zweiphasigen flüssigen Gemisch in der Nähe von dessen kritischem Punkt vollständig benetzt.[22] Benetzt eine der im Verlauf einer spinodalen Entmischung entstehenden koexistierenden Phasen eine Grenzfläche bevorzugt, ordnen sich die koexistierenden Phasen in Schichten parallel zur Grenzfläche an. Erst nach mehreren Schichtabfolgen findet ein Übergang zur isotropen Volumenmorphologie statt.[23][24][25]

Weiterhin werden Entmischungsprozesse, die In begrenzenden Geometrien wie dünnen Filmen und zylindrischen Poren stattfinden, durch die dann vorhandenen geometrischen Begrenzungen beeinflusst.[24] Benetzt eine der im Verlauf einer Entmischung in einer zylindrischen Kapillare entstehenden koexistierenden Phasen die Kapillarwand bevorzugt, bildet sich zunächst eine hohlzylindrischen Schicht der die Kapillarwand benetzenden Phase zwischen der Kapillarwand und einer zylindrischen Domäne der zweiten Phase im Zentrum der Kapillare aus. Diese Struktur wandelt sich durch das Auftreten von Plateau-Rayleigh-Instabilitäten in eine "bambushalmartige" Struktur oder sogar in eine regelmäßige Abfolge diskreter sphärischer Domänen der die Kapillarwände nicht benetzenden Phase in der die Kapillarwände benetzenden Matrixphase um.[26] Für Gleichgewichtsentmischungsmorphologien, die Gemische innerhalb ihres Koexistenzgebietes in zylindrischen Kapillaren ausbilden und die von den Wechselwirkungen zwischen den koexistierenden Phasen und den Kapillarwänden abhängen, lassen sich wiederum Benetzungsphasendiagramme erstellen.[27]

Mikrophasenseparation

Transmissionselektronenmikroskopie-Bild von mikrophasensepariertem Polystyrol-block-Polybutadien-block-Polystyrol. Die Polybutatien-Matrix wurde mit Osmiumtretroxid angefärbt.

Blockcopolymere sind Makromoleküle, die aus kovalent verknüpften Segmenten bestehen. Die Segmente bestehen ihrerseits aus identischen Repetiereinheiten. Die Segmente eines Blockcopolymers sind in der Regel über weite Temperaturbereiche nicht miteinander kompatibel und entmischen. Da die Segmente kovalent aneinander gebunden sind, kann eine Entmischung nicht auf makroskopischer Ebene erfolgen. Stattdessen kommt es zu Mikrophasenseparation. Diese führt zur Ausbildung von Entmischungsmorphologien, die durch den Moleküldimensionen entsprechende mesoskopische Längenskalen gekennzeichnet sind. In vielen Fällen geht die Mikrophasenseparation mit Selbstassemblierung zu regelmäßig geordneten Mikrophasenstrukturen einher.[28][29] Die dabei erhaltenen Morphologien hängen von den Volumenbrüchen der Komponenten des Blockcopolymers sowie dem Ausmaß der Inkompabilität der Segmente der Blockcopolymer-Moleküle ab. In einem symmetrischen Diblockcopolymer, in dem die aus den beiden verschiedenen Segmenten gebildeten Phasen jeweils etwa die Hälfte des Volumens einnehmen, bildet sich eine schichtartig-lamellare Struktur. Nehmen die Domänen einer der Segmentspezies ein etwas größeres Volumen ein als die der anderen Segmentspezies, entsteht eine bikontinuierliche gyroidale Morphologie. Wird der Volumenanteil der Minoritätsdomänen weiter verringert, bilden die Minoritätssegmente zylindrische und schließlich sphärische Domänen, die jeweils in regelmäßigen Gittern angeordnet sind. Insbesondere die Erzeugung selbstgeordneter mikrophasenseparierter Blockcopolymer-Morphologien in dünnen Filmen hat großes Interesse gefunden.[30]

Technische und biologische Relevanz

Trennverfahren

Trennverfahren können auf Entmischungsprozessen oder der Gegenwart koexistierender Phasen beruhen. So werden bei der Flüssig-Flüssig-Extraktion die die verschiedenen Löslichkeiten von Stoffen in zwei nicht miteinander mischbaren Lösungsmitteln ausnutzt. Bei der Azeotroprektifikation wird einem azeotropen Gemisch ein Schleppmittel zugesetzt, so dass ein leichtsiedendes ternäres Heteroazeotrop durch Rektifikation aus dem Azeotrop abtrennbar ist und in einem Phasenscheider kondensiert. Durch Entmischung des Kondensats in eine schleppmittelreiche und eine schleppmittelarme Phase kann das Schleppmittel regeneriert und dem Ausgangsazeotrop wieder zugeführt werden.

Initiierung von Kristallisation

Kristallisation niedermolekularer Verbindungen aus übersättigten Lösungen ist ein Phasenübergang erster Ordnung, der nach klassischer Vorstellung die direkte Bildung kristalliner Keime aus der metastabilen flüssigen Phase beinhaltet. Neuere Erkenntnisse deuten darauf hin, dass in einem ersten Schritt eine Entmischung in der übersättigten Lösung stattfindet. Als Resultat bildet sich eine flüssige Phase aus, in der die kristallisationsfähige Spezies stark angereichert ist und innerhalb derer Nukeation und Kristallisation initiiert wird.[31][32]

Herstellung poröser Materialien

Spinodale Entmischung in viskosen flüssigen Gemischen kann zur Herstellung poröser Monolithe und Membranen mit kontinuierlich-schwammartigen Porensystemen genutzt werden. Poröse Polymermaterialien lassen sich erzeugen, indem die stoffliche Zusammensetzung einer Lösung eines Polymers oder mehrerer Polymere durch Verdunstung des Lösungsmittels verändert wird. Die Änderung der Lösungszusammensetzung löst eine spinodale Entmischung in eine polymerreiche und eine lösungsmittelreiche Phase aus. Wird der Lösungsmittelanteil des phasenseparierten Gemisches weiter verringert, etwa durch fortgesetzte Verdunstung, kann sich die polymerreiche Phase durch Verglasung oder Kristallisation verfestigen, während aus dem von der lösungsmittelreichen Phase eingenommenen Volumen das Porensystem entsteht.[33][34] Nichtlösungsmittel-induzierte Phasenseparation (nonsolvent-induced phase separation, übliches Akronym NIPS) beinhaltet die Herstellung poröser Polymermembranen durch eine Phasenseparation, die beim Mischen einer Lösung des Polymers in einem guten Lösungsmittel mit einem Überschuss Nichtlösungsmittel auftritt.[35] Die Herstellung anorganischer poröser Gläser, beispielsweise durch den VYCOR-Prozess, beruht auf einer durch Abkühlen der Schmelze eines homogenen Alkaliborosilikat-Ausgangsglases in dessen Mischungslücke ausgelösten spinodalen Entmischung. In einem weiteren Kühlschritt erstarrt das phasenseparierte Gemisch. Schließlich wird eine der gebildeten koexistierenden Phasen durch selektive Extraktion entfernt, so dass an deren Stelle Poren entstehen. Die Porenmorphologie des erhaltenen porösen Glases hängt unter anderem von der Zusammensetzung des verwendeten Ausgangsglases und der Steuerung der spinodalen Entmischung ab.[36]

Herstellung funktionaler nanostrukturierter Materialien

Entmischungsprozesse können auch zur Herstellung nanostrukturierter funktionaler Materialien eingesetzt werden. So wurde Entmischung eingesetzt, um nanostrukturierte thermoelektrische Materialien auf Basis des Bleitellurid-Bleisulfid-Systems herzustellen, die niedrige Wärmeleitfähigkeiten mit hoher Elektronenmobilität kombinieren und daher bessere thermoelektrische Eigenschaften aufweisen als reines Bleitellurid.[37]

Biologische Relevanz

Biologische Zellen organisieren zahlreiche biochemische Prozesse in Zellkompartimenten, die nicht durch eine Biomembran von ihrer Umgebung abgegrenzt sind. Entmischungsprozesse sind eine Form zellulärer Organisation, die zur Bildung derartiger nicht biomembranbegrenzter Zellkompartimente im Cytoplasma führt.[38] Organellen, die aus nicht biomembranbegrenzten Zellkompartimenten bestehen, werden als biomolekulares Kondensat bezeichnet.[39]

Literatur

Gernot Kostorz (Hrsg.): Phase Transformations in Materials. 1. Auflage. Wiley, 2001, ISBN 3-527-30256-5, doi:10.1002/352760264x.

Einzelnachweise

J. B. Clarke, J. W. Hastie, L. H. E. Kihlborg, R. Metselaar und M. M. Thackeray: Definitions of terms relating to phase transitions of the solid state (IUPAC Recommendations 1994). In: Pure and Applied Chemistry. Band 66, Nr. 3, 1994, S. 577–594, doi:10.1351/pac199466030577.
Kenneth Denbigh: The Principles of Chemical Equilibrium: With Applications in Chemistry and Chemical Engineering. 4. Auflage, Cambridge University Press, Cambridge 1981, ISBN 0-521-28150-4, doi:10.1017/CBO9781139167604, S. 184.
Burkhard Lohrengel: Thermische Trennverfahren: Trennung von Gas-, Dampf- und Flüssigkeitsgemischen. 3. Auflage. Walter de Gruyter, Berlin 2017, ISBN 978-3-11-047352-0. Siehe Kapitel "4.4.2 Teilweise Löslichkeit von Trägerstoff und Extraktionsmittel".
Gert R. Strobl: The physics of polymers: concepts for understanding their structures and behavior. 3. Auflage. Springer, Berlin/Heidelberg/New York 2007, ISBN 978-3-540-68411-4, S. 105 ff., doi:10.1007/978-3-540-68411-4.
Günter Jakob Lauth, Jürgen Kowalczyk: Thermodynamik – Eine Einführung. Springer, Berlin/Heidelberg 2015, ISBN 978-3-662-46228-7, Kapitel "18 Nicht vollständig mischbare Mehrkomponentensysteme und deren Phasendiagramme", doi:10.1007/978-3-662-46229-4 (springer.com [abgerufen am 3. Februar 2021]).
W. J. Work, K. Horie, M. Hess, R. F. T. Stepto: Definition of terms related to polymer blends, composites, and multiphase polymeric materials (IUPAC Recommendations 2004). In: Pure and Applied Chemistry. Band 76, Nr. 11, 1. Januar 2004, ISSN 1365-3075, S. 1985–2007, doi:10.1351/pac200476111985.
J. Willard Gibbs: On the equilibrium of heterogeneous substances. In: Transactions of the Connecticut Academy of Arts and Sciences. Band 3, 1874–1878, S. 108–248. Abrufbar unter https://www.biodiversitylibrary.org/item/32295#page/128/mode/thum abgerufen am 27. Januar 2021.
J. Willard Gibbs: On the equilibrium of heterogeneous substances. In: Transactions of the Connecticut Academy of Arts and Sciences. Band 3, 1874–1878, S. 343–524. Abrufbar unter https://www.biodiversitylibrary.org/item/88413#page/437/mode/1up abgerufen am 27. Januar 2021.
John W. Cahn, John E. Hilliard: Free Energy of a Nonuniform System. III. Nucleation in a Two‐Component Incompressible Fluid. In: The Journal of Chemical Physics. Band 31, Nr. 3, September 1959, ISSN 0021-9606, S. 688–699, doi:10.1063/1.1730447.
K. Binder: Collective diffusion, nucleation, and spinodal decomposition in polymer mixtures. In: The Journal of Chemical Physics. Band 79, Nr. 12, 15. Dezember 1983, ISSN 0021-9606, S. 6387–6409, doi:10.1063/1.445747.
K Binder: Theory of first-order phase transitions. In: Reports on Progress in Physics. 50, Nr. 7, 1. Juli 1987, ISSN 0034-4885, S. 783–859. doi:10.1088/0034-4885/50/7/001.
Andrew Keller, Stephen Z.D. Cheng: The role of metastability in polymer phase transitions. In: Polymer. Band 39, Nr. 19, September 1998, S. 4461–4487, doi:10.1016/S0032-3861(97)10320-2.
W. C. Carter: Cahn-Hilliard Equation. Website des NIST. Abgerufen am 21. Januar 2021.
J. E. Hilliard, J. W. Cahn: Free energy of a non uniform system I. Interfacial Free Energy. In: Journal of Chemical Physics. Band 28, Nr. 2, 1958, S. 258–267, doi:10.1063/1.1744102.
J. W. Cahn: On spinodal decomposition. In: Acta Metallurgica. Band 9, Nr. 9, 1961, S. 795–801, doi:10.1016/0001-6160(61)90182-1.
J. W. Cahn: Phase Separation by Spinodal Decomposition in Isotropic Systems. In: Journal of Chemical Physics. Band 42, Nr. 1, 1965, S. 93–99, doi:10.1063/1.1695731.
John W Cahn: The later stages of spinodal decomposition and the beginnings of particle coarsening. In: Acta Metallurgica. Band 14, Nr. 12, Dezember 1966, S. 1685–1692, doi:10.1016/0001-6160(66)90021-6.
Eric D. Siggia: Late stages of spinodal decomposition in binary mixtures. In: Physical Review A. Band 20, Nr. 2, 1. August 1979, ISSN 0556-2791, S. 595–605, doi:10.1103/PhysRevA.20.595.
P. G. de Gennes: Dynamics of fluctuations and spinodal decomposition in polymer blends. In: The Journal of Chemical Physics. Band 72, Nr. 9, Mai 1980, ISSN 0021-9606, S. 4756–4763, doi:10.1063/1.439809.
A.J. Bray: Theory of phase-ordering kinetics. In: Advances in Physics. Band 43, Nr. 3, Juni 1994, ISSN 0001-8732, S. 357–459, doi:10.1080/00018739400101505.
Daniel Bonn, David Ross: Wetting transitions. In: Reports on Progress in Physics. Band 64, Nr. 9, 1. September 2001, ISSN 0034-4885, S. 1085–1163, doi:10.1088/0034-4885/64/9/202.
J. W. Cahn: Critical Point Wetting. In: Journal of Chemical Physics. Band 66, Nr. 8, 1977, S. 3667–3672, doi:10.1063/1.434402.
Richard A. L. Jones, Laura J. Norton, Edward J. Kramer, Frank S. Bates, Pierre Wiltzius: Surface-directed spinodal decomposition. In: Physical Review Letters. Band 66, Nr. 10, 11. März 1991, ISSN 0031-9007, S. 1326–1329, doi:10.1103/PhysRevLett.66.1326.
Review Article. In: Journal of Non-Equilibrium Thermodynamics. Band 23, Nr. 1, 1998, ISSN 0340-0204, S. 1–44, doi:10.1515/jnet.1998.23.1.1.
Y Lipatov: Polymer blends and interpenetrating polymer networks at the interface with solids. In: Progress in Polymer Science. Band 27, Nr. 9, November 2002, S. 1721–1801, doi:10.1016/S0079-6700(02)00021-7.
Hajime Tanaka: Dynamic interplay between phase separation and wetting in a binary mixture confined in a one-dimensional capillary. In: Physical Review Letters. Band 70, Nr. 1, 4. Januar 1993, ISSN 0031-9007, S. 53–56, doi:10.1103/PhysRevLett.70.53.
Andrea Liu, D. Durian, Eric Herbolzheimer, S. Safran: Wetting transitions in a cylindrical pore. In: Physical Review Letters. Band 65, Nr. 15, Oktober 1990, ISSN 0031-9007, S. 1897–1900, doi:10.1103/physrevlett.65.1897.
Frank S. Bates, Glenn H. Fredrickson: Block Copolymer Thermodynamics: Theory and Experiment. In: Annual Review of Physical Chemistry. Band 41, Nr. 1, Oktober 1990, ISSN 0066-426X, S. 525–557, doi:10.1146/annurev.pc.41.100190.002521.
Volker Abetz, Peter F. W. Simon: Phase Behaviour and Morphologies of Block Copolymers. In: Block Copolymers I. Band 189. Springer-Verlag, Berlin/Heidelberg 2005, ISBN 978-3-540-26580-1, S. 125–212, doi:10.1007/12_004.
IW Hamley: Ordering in Thin Films of Block Copolymers: Fundamentals to Potential Applications. In: Progress in Polymer Science. 34, Nr. 11, 2009, S. 1161–1210. doi:10.1016/j.progpolymsci.2009.06.003.
Peter G. Vekilov: The two-step mechanism of nucleation of crystals in solution. In: Nanoscale. Band 2, Nr. 11, 2010, ISSN 2040-3364, S. 2346, doi:10.1039/c0nr00628a.
Denis Gebauer, Matthias Kellermeier, Julian D. Gale, Lennart Bergström, Helmut Cölfen: Pre-nucleation clusters as solute precursors in crystallisation. In: Chem. Soc. Rev. Band 43, Nr. 7, 2014, ISSN 0306-0012, S. 2348–2371, doi:10.1039/C3CS60451A.
J. Arnouts, H. Berghmans: Amorphous thermoreversible gels of atactic polystyrene. In: Polymer Communications. Band 28, 1987, S. 66–68.
P. van de Witte, P.J. Dijkstra, J.W.A. van den Berg, J. Feijen: Phase separation processes in polymer solutions in relation to membrane formation. In: Journal of Membrane Science. Band 117, Nr. 1-2, August 1996, S. 1–31, doi:10.1016/0376-7388(96)00088-9.
Da-Ming Wang, Juin-Yih Lai: Recent advances in preparation and morphology control of polymeric membranes formed by nonsolvent induced phase separation. In: Current Opinion in Chemical Engineering. Band 2, Nr. 2, Mai 2013, S. 229–237, doi:10.1016/j.coche.2013.04.003 (elsevier.com [abgerufen am 25. April 2021]).
D. Enke, F. Janowski, W. Schwieger: Porous glasses in the 21st century–a short review. In: Microporous and Mesoporous Materials. Band 60, Nr. 1-3, Juni 2003, S. 19–30, doi:10.1016/S1387-1811(03)00329-9.
John Androulakis, Chia-Her Lin, Hun-Jin Kong, Ctirad Uher, Chun-I Wu: Spinodal Decomposition and Nucleation and Growth as a Means to Bulk Nanostructured Thermoelectrics: Enhanced Performance in Pb_1-x Sn_x Te−PbS. In: Journal of the American Chemical Society. Band 129, Nr. 31, August 2007, ISSN 0002-7863, S. 9780–9788, doi:10.1021/ja071875h.
Anthony A. Hyman, Christoph A. Weber, Frank Jülicher: Liquid-Liquid Phase Separation in Biology. In: Annual Review of Cell and Developmental Biology. Band 30, Nr. 1, 11. Oktober 2014, ISSN 1081-0706, S. 39–58, doi:10.1146/annurev-cellbio-100913-013325.
Simon Alberti: Phase separation in biology. In: Current Biology. Band 27, Nr. 20, Oktober 2017, S. R1097–R1102, doi:10.1016/j.cub.2017.08.069.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Clarke1994-1] J. B. Clarke, J. W. Hastie, L. H. E. Kihlborg, R. Metselaar und M. M. Thackeray: Definitions of terms relating to phase transitions of the solid state (IUPAC Recommendations 1994). In: Pure and Applied Chemistry. Band 66, Nr. 3, 1994, S. 577–594, doi:10.1351/pac199466030577.

[Denbigh_184-2] Kenneth Denbigh: The Principles of Chemical Equilibrium: With Applications in Chemistry and Chemical Engineering. 4. Auflage, Cambridge University Press, Cambridge 1981, ISBN 0-521-28150-4, doi:10.1017/CBO9781139167604, S. 184.

[3] Burkhard Lohrengel: Thermische Trennverfahren: Trennung von Gas-, Dampf- und Flüssigkeitsgemischen. 3. Auflage. Walter de Gruyter, Berlin 2017, ISBN 978-3-11-047352-0. Siehe Kapitel "4.4.2 Teilweise Löslichkeit von Trägerstoff und Extraktionsmittel".

[4] Gert R. Strobl: The physics of polymers: concepts for understanding their structures and behavior. 3. Auflage. Springer, Berlin/Heidelberg/New York 2007, ISBN 978-3-540-68411-4, S. 105 ff., doi:10.1007/978-3-540-68411-4.

[5] Günter Jakob Lauth, Jürgen Kowalczyk: Thermodynamik – Eine Einführung. Springer, Berlin/Heidelberg 2015, ISBN 978-3-662-46228-7, Kapitel "18 Nicht vollständig mischbare Mehrkomponentensysteme und deren Phasendiagramme", doi:10.1007/978-3-662-46229-4 (springer.com [abgerufen am 3. Februar 2021]).

[morphdom-6] W. J. Work, K. Horie, M. Hess, R. F. T. Stepto: Definition of terms related to polymer blends, composites, and multiphase polymeric materials (IUPAC Recommendations 2004). In: Pure and Applied Chemistry. Band 76, Nr. 11, 1. Januar 2004, ISSN 1365-3075, S. 1985–2007, doi:10.1351/pac200476111985.

[7] J. Willard Gibbs: On the equilibrium of heterogeneous substances. In: Transactions of the Connecticut Academy of Arts and Sciences. Band 3, 1874–1878, S. 108–248. Abrufbar unter https://www.biodiversitylibrary.org/item/32295#page/128/mode/thum abgerufen am 27. Januar 2021.

[8] J. Willard Gibbs: On the equilibrium of heterogeneous substances. In: Transactions of the Connecticut Academy of Arts and Sciences. Band 3, 1874–1878, S. 343–524. Abrufbar unter https://www.biodiversitylibrary.org/item/88413#page/437/mode/1up abgerufen am 27. Januar 2021.

[9] John W. Cahn, John E. Hilliard: Free Energy of a Nonuniform System. III. Nucleation in a Two‐Component Incompressible Fluid. In: The Journal of Chemical Physics. Band 31, Nr. 3, September 1959, ISSN 0021-9606, S. 688–699, doi:10.1063/1.1730447.

[10] K. Binder: Collective diffusion, nucleation, and spinodal decomposition in polymer mixtures. In: The Journal of Chemical Physics. Band 79, Nr. 12, 15. Dezember 1983, ISSN 0021-9606, S. 6387–6409, doi:10.1063/1.445747.

[11] K Binder: Theory of first-order phase transitions. In: Reports on Progress in Physics. 50, Nr. 7, 1. Juli 1987, ISSN 0034-4885, S. 783–859. doi:10.1088/0034-4885/50/7/001.

[12] Andrew Keller, Stephen Z.D. Cheng: The role of metastability in polymer phase transitions. In: Polymer. Band 39, Nr. 19, September 1998, S. 4461–4487, doi:10.1016/S0032-3861(97)10320-2.

[13] W. C. Carter: Cahn-Hilliard Equation. Website des NIST. Abgerufen am 21. Januar 2021.

[14] J. E. Hilliard, J. W. Cahn: Free energy of a non uniform system I. Interfacial Free Energy. In: Journal of Chemical Physics. Band 28, Nr. 2, 1958, S. 258–267, doi:10.1063/1.1744102.

[15] J. W. Cahn: On spinodal decomposition. In: Acta Metallurgica. Band 9, Nr. 9, 1961, S. 795–801, doi:10.1016/0001-6160(61)90182-1.

[16] J. W. Cahn: Phase Separation by Spinodal Decomposition in Isotropic Systems. In: Journal of Chemical Physics. Band 42, Nr. 1, 1965, S. 93–99, doi:10.1063/1.1695731.

[17] John W Cahn: The later stages of spinodal decomposition and the beginnings of particle coarsening. In: Acta Metallurgica. Band 14, Nr. 12, Dezember 1966, S. 1685–1692, doi:10.1016/0001-6160(66)90021-6.

[18] Eric D. Siggia: Late stages of spinodal decomposition in binary mixtures. In: Physical Review A. Band 20, Nr. 2, 1. August 1979, ISSN 0556-2791, S. 595–605, doi:10.1103/PhysRevA.20.595.

[19] P. G. de Gennes: Dynamics of fluctuations and spinodal decomposition in polymer blends. In: The Journal of Chemical Physics. Band 72, Nr. 9, Mai 1980, ISSN 0021-9606, S. 4756–4763, doi:10.1063/1.439809.

[20] A.J. Bray: Theory of phase-ordering kinetics. In: Advances in Physics. Band 43, Nr. 3, Juni 1994, ISSN 0001-8732, S. 357–459, doi:10.1080/00018739400101505.

[21] Daniel Bonn, David Ross: Wetting transitions. In: Reports on Progress in Physics. Band 64, Nr. 9, 1. September 2001, ISSN 0034-4885, S. 1085–1163, doi:10.1088/0034-4885/64/9/202.

[22] J. W. Cahn: Critical Point Wetting. In: Journal of Chemical Physics. Band 66, Nr. 8, 1977, S. 3667–3672, doi:10.1063/1.434402.

[23] Richard A. L. Jones, Laura J. Norton, Edward J. Kramer, Frank S. Bates, Pierre Wiltzius: Surface-directed spinodal decomposition. In: Physical Review Letters. Band 66, Nr. 10, 11. März 1991, ISSN 0031-9007, S. 1326–1329, doi:10.1103/PhysRevLett.66.1326.

[Binder1998-24] Review Article. In: Journal of Non-Equilibrium Thermodynamics. Band 23, Nr. 1, 1998, ISSN 0340-0204, S. 1–44, doi:10.1515/jnet.1998.23.1.1.

[25] Y Lipatov: Polymer blends and interpenetrating polymer networks at the interface with solids. In: Progress in Polymer Science. Band 27, Nr. 9, November 2002, S. 1721–1801, doi:10.1016/S0079-6700(02)00021-7.

[26] Hajime Tanaka: Dynamic interplay between phase separation and wetting in a binary mixture confined in a one-dimensional capillary. In: Physical Review Letters. Band 70, Nr. 1, 4. Januar 1993, ISSN 0031-9007, S. 53–56, doi:10.1103/PhysRevLett.70.53.

[27] Andrea Liu, D. Durian, Eric Herbolzheimer, S. Safran: Wetting transitions in a cylindrical pore. In: Physical Review Letters. Band 65, Nr. 15, Oktober 1990, ISSN 0031-9007, S. 1897–1900, doi:10.1103/physrevlett.65.1897.

[28] Frank S. Bates, Glenn H. Fredrickson: Block Copolymer Thermodynamics: Theory and Experiment. In: Annual Review of Physical Chemistry. Band 41, Nr. 1, Oktober 1990, ISSN 0066-426X, S. 525–557, doi:10.1146/annurev.pc.41.100190.002521.

[29] Volker Abetz, Peter F. W. Simon: Phase Behaviour and Morphologies of Block Copolymers. In: Block Copolymers I. Band 189. Springer-Verlag, Berlin/Heidelberg 2005, ISBN 978-3-540-26580-1, S. 125–212, doi:10.1007/12_004.

[30] IW Hamley: Ordering in Thin Films of Block Copolymers: Fundamentals to Potential Applications. In: Progress in Polymer Science. 34, Nr. 11, 2009, S. 1161–1210. doi:10.1016/j.progpolymsci.2009.06.003.

[31] Peter G. Vekilov: The two-step mechanism of nucleation of crystals in solution. In: Nanoscale. Band 2, Nr. 11, 2010, ISSN 2040-3364, S. 2346, doi:10.1039/c0nr00628a.

[32] Denis Gebauer, Matthias Kellermeier, Julian D. Gale, Lennart Bergström, Helmut Cölfen: Pre-nucleation clusters as solute precursors in crystallisation. In: Chem. Soc. Rev. Band 43, Nr. 7, 2014, ISSN 0306-0012, S. 2348–2371, doi:10.1039/C3CS60451A.

[33] J. Arnouts, H. Berghmans: Amorphous thermoreversible gels of atactic polystyrene. In: Polymer Communications. Band 28, 1987, S. 66–68.

[34] P. van de Witte, P.J. Dijkstra, J.W.A. van den Berg, J. Feijen: Phase separation processes in polymer solutions in relation to membrane formation. In: Journal of Membrane Science. Band 117, Nr. 1-2, August 1996, S. 1–31, doi:10.1016/0376-7388(96)00088-9.

[35] Da-Ming Wang, Juin-Yih Lai: Recent advances in preparation and morphology control of polymeric membranes formed by nonsolvent induced phase separation. In: Current Opinion in Chemical Engineering. Band 2, Nr. 2, Mai 2013, S. 229–237, doi:10.1016/j.coche.2013.04.003 (elsevier.com [abgerufen am 25. April 2021]).

[36] D. Enke, F. Janowski, W. Schwieger: Porous glasses in the 21st century–a short review. In: Microporous and Mesoporous Materials. Band 60, Nr. 1-3, Juni 2003, S. 19–30, doi:10.1016/S1387-1811(03)00329-9.

[37] John Androulakis, Chia-Her Lin, Hun-Jin Kong, Ctirad Uher, Chun-I Wu: Spinodal Decomposition and Nucleation and Growth as a Means to Bulk Nanostructured Thermoelectrics: Enhanced Performance in Pb_1-x Sn_x Te−PbS. In: Journal of the American Chemical Society. Band 129, Nr. 31, August 2007, ISSN 0002-7863, S. 9780–9788, doi:10.1021/ja071875h.

[38] Anthony A. Hyman, Christoph A. Weber, Frank Jülicher: Liquid-Liquid Phase Separation in Biology. In: Annual Review of Cell and Developmental Biology. Band 30, Nr. 1, 11. Oktober 2014, ISSN 1081-0706, S. 39–58, doi:10.1146/annurev-cellbio-100913-013325.

[39] Simon Alberti: Phase separation in biology. In: Current Biology. Band 27, Nr. 20, Oktober 2017, S. R1097–R1102, doi:10.1016/j.cub.2017.08.069.