Binodale

Als Binodale wird eine Phasengrenzlinie im Zustandsraum eines thermodynamischen Systems bezeichnet, die ein Koexistenzgebiet von einem Einphasengebiet abgrenzt und dabei einen als kritischer Punkt bezeichneten Extremwert aufweist. Die Zustände, welche die miteinander im thermodynamischen Gleichgewicht stehenden koexistierenden Phasen innerhalb des Koexistenzgebietes repräsentieren, sind beiderseits des kritischen Punktes lokalisiert und werden durch Konoden verbunden. Wird im Verlauf einer Zustandsänderung die Binodale überquert, findet ein Phasenübergang statt, der zur Bildung koexistierender Phasen aus einer homogenen Phase oder zur Bildung einer homogenen Phase aus koexistierenden Phasen führt.[1][2][3]

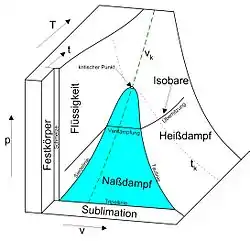
Druck-Volumen-Temperatur-Diagramm eines Reinstoffes. Die Koexistenzkurve umschließt das blau kolorierte Koexistenzgebiet der flüssigen Phase und der Gasphase.

Thermodynamische Einordnung

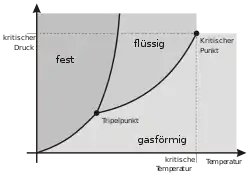
Projektion des Druck-Volumen-Temperatur-Diagramms eines Reinstoffes in die Druck-Temperatur-Ebene (die y-Achse ist die Druckachse). Die das Koexistenzgebiet von flüssiger Phase und Gasphase umschließende Koexistenzkurve erscheint als Verbindungslinie zwischen Tripelpunkt und kritischem Punkt.

Zustände, die koexistierende Phasen repräsentieren, müssen sich zumindest in einer Zustandsgröße unterscheiden, wobei es sich um extensive Zustandsgrößen, wie die Zusammensetzung von Gemischen und das absolute Volumen, oder um intensive Zustandsgrößen, wie das molare Volumen und die Dichte, handeln kann. Hingegen nimmt nach dem nullten Hauptsatz der Thermodynamik die Temperatur, bei der es sich ihrerseits um eine intensive Zustandsgrößen handelt, in allen miteinander im Gleichgewicht stehenden koexistierenden Phasen immer denselben Wert an. Auch der Druck als weitere intensive Zustandsgröße muss in allen im Gleichgewicht stehenden Phasen gleich groß sein (siehe Abschnitt Phasenregel für nicht chemisch reagierende Substanzen im Artikel Gibbssche Phasenregel).[4] Wird die freie Enthalpie eines thermodynamischen Systems, in dem koexistierende Phasen vorliegen, als Funktion einer Zustandsgröße, in der sich die koexistierenden Phasen unterscheiden, aufgetragen, weist die erhaltene Kurve zwei Minima auf. Diese Minima markieren die Zustände, in denen die miteinander im Gleichgewicht stehenden koexistierenden Phasen vorliegen. Das Mengenverhältnis, in dem die koexistierenden Phasen vorliegen, lässt sich mit Hilfe der Konodenregel ermitteln.[5] Wird die freie Enthalpie als Funktion der die Zustände der koexistierenden Phasen unterscheidenden Zustandsgröße für verschiedene Werte einer weiteren intensiven Zustandsgröße ermittelt, die in allen koexistierenden Phasen denselben Wert besitzt, bilden die Minima der so erhaltenen Profile der freien Enthalpie im Zustandsraum des betrachteten thermodynamischen Systems die Binodale.[6]

Kritische Punkte können sowohl in Form von Maxima als auch in Form von Minima vorliegen. Nähert man das betrachtete System durch Änderung einer der intensiven Zustandsgrößen, die in den koexistierenden Phasen denselben Wert besitzen, aus dem Koexistenzgebiet heraus einem kritischen Punkt an, rücken die Minima der freien Enthalpie als Funktion der die koexistierenden Phasen unterscheidenden Zustandsgröße zusammen. Folgedessen nähern sich die Eigenschaften der koexistierenden Phasen an. Am kritischen Punkt werden die Eigenschaften der koexistierenden Phasen innerhalb des Koexistenzgebiets sowie der außerhalb existierenden homogenen Phase ununterscheidbar.[7] Die Binodale umschließt weiterhin die innerhalb des Koexistenzgebietes verlaufende Spinodale, mit der sie lediglich die kritischen Punkte gemeinsam hat.[3] Innerhalb des Koexistenzgebietes ist eine homogene Phase im Bereich zwischen Binodaler und Spinodaler metastabil. Die Umwandlung der metastabilen homogenen Phase in die stabilen koexistierenden Phasen verläuft dort über einen Nukleationsmechanismus[8][9] und kann hinsichtlich ihres zeitlichen Verlaufs durch die Johnson-Mehl-Avrami-Kolmogorow-Gleichung beschrieben werden.

Beispiele

Fluide Reinstoffe

In den in Druck-Volumen-Temperatur-Diagrammen dargestellten Zustandsflächen fluider Reinstoffe treten Koexistenzgebiete von flüssiger Phase und Gasphase auf, die von einer hier meist als Koexistenzkurve bezeichneten Binodalen umschlossen werden.[2] Beim Übertritt von der flüssigen Phase in das Koexistenzgebiet verdampft die Flüssigkeit. Beim Übertritt aus der Gasphase in das Koexistenzgebiet kondensiert das Gas.

In in die Druck-Volumen-Ebene projizierten Phasendiagrammen weist die Koexistenzkurve ein Maximum am kritischen Punkt auf und läuft mit zunehmendem Volumen asymptotisch gegen die Volumenachse. In in die Druck-Temperatur-Ebene projizierten Phasendiagrammen erscheint die Koexistenzkurve als Linie, die den Tripelpunkt mit dem kritischen Punkt verbindet und die als Siedepunktskurve bezeichnet wird. Der Grund hierfür ist, dass koexistierenden Phasen jeweils im thermischen Gleichgewicht stehen und daher dieselbe Temperatur und denselben Druck besitzen müssen. Die Konoden verlaufen somit parallel zur Volumenachse und stehen senkrecht auf der Druck-Temperatur-Ebene. In der Druck-Temperatur-Ebene fallen die Äste der Koexistenzkurve beiderseits des kritischen Punktes folgedessen zusammen.[10]

Gemische

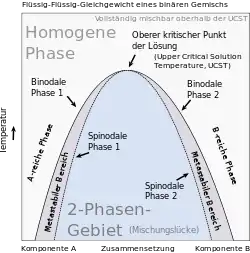
Temperatur-Zusammensetzungs-Phasendiagramm eines Gemisches.

Gemische können eine Mischungslücke aufweisen, die von einer Binodalen umgrenzt ist. Die kritischen Punkte von Binodalen im Zustandsraum von Gemischen sind, wenn es sich um Maxima handelt, durch obere, und wenn es sich um Minima handelt, durch untere kritische Lösungstemperaturen gennzeichnet. Außerhalb der Mischungslücke liegt das Gemisch im Gleichgewicht als homogene Mischphase vor, während es innerhalb der Mischungslücke koexistierende Phasen bildet. Wird ein Gemisch durch eine Zustandsänderung von einem Zustand, in dem eine homogene Mischphase stabil ist, durch Überquerung der Binodale in einen Zustand innerhalb einer Mischungslücke überführt, tritt Entmischung ein. Umgekehrt vereinigen sich koexistierende Phasen zu einer homogenen Mischphase, wenn das Gemisch aus einer Mischungslücke in einen Bereich des Zustandsraumes überführt wird, in dem es als homogene Mischphase stabil ist.

Binodalen von Gemischen werden häufig in Temperatur-Zusammensetzungs-Phasendiagramme oder in Dreiecksdiagramme[11][12] projiziert, wobei letztere die Zusammensetzung ternärer Gemische darstellen. Die Schnittpunkte der Konoden mit den Binodalen definieren dabei jeweils die Zusammensetzungen der innerhalb einer Mischungslücke koexistierenden Phasen.[7]

Siehe auch

Literatur

Pablo G. Debenedetti: Metastable liquids: concepts and principles. Princeton University Press, Princeton, N.J. 1996, ISBN 0-691-08595-1.
Bruno Predel, Michael Hoch, Monte Pool: Phase Diagrams and Heterogeneous Equilibria: a Practical Introduction. Springer-Verlag, Berlin/Heidelberg 2004, ISBN 978-3-662-09276-7, doi:10.1007/978-3-662-09276-7.
Peter Stephan, Karlheinz Schaber, Karl Stephan, Franz Mayinger: Thermodynamik – Grundlagen und technische Anwendungen. 2: Mehrstoffsysteme und chemische Reaktionen. Springer-Verlag, Berlin 2017, doi:10.1007/978-3-662-54439-6.

Einzelnachweise

J. B. Clarke, J. W. Hastie, L. H. E. Kihlborg, R. Metselaar und M. M. Thackeray: Definitions of terms relating to phase transitions of the solid state (IUPAC Recommendations 1994). In: Pure and Applied Chemistry. Band 66, Nr. 3, 1994, S. 577–594, doi:10.1351/pac199466030577.
Pablo G. Debenedetti: Metastable liquids: concepts and principles. Princeton University Press, Princeton, N.J. 1996, ISBN 0-691-08595-1, S. 69 ff.
Pierre Papon, Jacques Leblond, Paul H. E. Meijer: The physics of phase transitions: concepts and applications. 2. Auflage. Springer-Verlag, Berlin 2006, ISBN 978-3-540-33390-6, S. 132 ff.
Kenneth Denbigh: The Principles of Chemical Equilibrium: With Applications in Chemistry and Chemical Engineering. 4. Auflage, Cambridge University Press, Cambridge 1981, ISBN 0-521-28150-4, doi:10.1017/CBO9781139167604, S. 184.
Bruno Predel, Michael Hoch, Monte Pool: Phase Diagrams and Heterogeneous Equilibria: a Practical Introduction. Springer-Verlag, Berlin/Heidelberg 2004, ISBN 978-3-662-09276-7, Kapitel "3.8 The Lever Rule", doi:10.1007/978-3-662-09276-7.
Günter Jakob Lauth, Jürgen Kowalczyk: Thermodynamik – Eine Einführung. Springer, Berlin/Heidelberg 2015, ISBN 978-3-662-46228-7, Kapitel "18 Nicht vollständig mischbare Mehrkomponentensysteme und deren Phasendiagramme", doi:10.1007/978-3-662-46229-4 (springer.com [abgerufen am 3. Februar 2021]).
Gert R. Strobl: The physics of polymers: concepts for understanding their structures and behavior. 3. Auflage. Springer, Berlin/Heidelberg/New York 2007, ISBN 978-3-540-68411-4, S. 105 ff., doi:10.1007/978-3-540-68411-4.
John W. Cahn, John E. Hilliard: Free Energy of a Nonuniform System. III. Nucleation in a Two‐Component Incompressible Fluid. In: The Journal of Chemical Physics. Band 31, Nr. 3, September 1959, ISSN 0021-9606, S. 688–699, doi:10.1063/1.1730447 (scitation.org [abgerufen am 27. Januar 2021]).
K Binder: Theory of first-order phase transitions. In: Reports on Progress in Physics. 50, Nr. 7, 1. Juli 1987, ISSN 0034-4885, S. 783–859. doi:10.1088/0034-4885/50/7/001.
Klaus Stierstadt: Thermodynamik (= Springer-Lehrbuch). Springer-Verlag, Berlin/Heidelberg 2010, ISBN 978-3-642-05097-8, doi:10.1007/978-3-642-05098-5. Siehe Kapitel 9, Abbildung 9.5.
Bruno Predel, Michael Hoch, Monte Pool: Phase Diagrams and Heterogeneous Equilibria: a Practical Introduction. Springer-Verlag, Berlin/Heidelberg 2004, ISBN 978-3-662-09276-7, Kapitel "4 Phase Equilibria in Three-Component Systems and Four-Component Systems with Exclusion of the Gas Phase", doi:10.1007/978-3-662-09276-7.
Burkhard Lohrengel: Thermische Trennverfahren: Trennung von Gas-, Dampf- und Flüssigkeitsgemischen. 3. Auflage. Walter de Gruyter, Berlin/Boston 2017, ISBN 978-3-11-047322-3, Kapitel "4.4.2 Teilweise Löslichkeit von Trägerstoff und Extraktionsmittel".

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Clarke1994-1] J. B. Clarke, J. W. Hastie, L. H. E. Kihlborg, R. Metselaar und M. M. Thackeray: Definitions of terms relating to phase transitions of the solid state (IUPAC Recommendations 1994). In: Pure and Applied Chemistry. Band 66, Nr. 3, 1994, S. 577–594, doi:10.1351/pac199466030577.

[Debenedetti-2] Pablo G. Debenedetti: Metastable liquids: concepts and principles. Princeton University Press, Princeton, N.J. 1996, ISBN 0-691-08595-1, S. 69 ff.

[phase_transitions-3] Pierre Papon, Jacques Leblond, Paul H. E. Meijer: The physics of phase transitions: concepts and applications. 2. Auflage. Springer-Verlag, Berlin 2006, ISBN 978-3-540-33390-6, S. 132 ff.

[Denbigh_184-4] Kenneth Denbigh: The Principles of Chemical Equilibrium: With Applications in Chemistry and Chemical Engineering. 4. Auflage, Cambridge University Press, Cambridge 1981, ISBN 0-521-28150-4, doi:10.1017/CBO9781139167604, S. 184.

[5] Bruno Predel, Michael Hoch, Monte Pool: Phase Diagrams and Heterogeneous Equilibria: a Practical Introduction. Springer-Verlag, Berlin/Heidelberg 2004, ISBN 978-3-662-09276-7, Kapitel "3.8 The Lever Rule", doi:10.1007/978-3-662-09276-7.

[6] Günter Jakob Lauth, Jürgen Kowalczyk: Thermodynamik – Eine Einführung. Springer, Berlin/Heidelberg 2015, ISBN 978-3-662-46228-7, Kapitel "18 Nicht vollständig mischbare Mehrkomponentensysteme und deren Phasendiagramme", doi:10.1007/978-3-662-46229-4 (springer.com [abgerufen am 3. Februar 2021]).

[Strobl-7] Gert R. Strobl: The physics of polymers: concepts for understanding their structures and behavior. 3. Auflage. Springer, Berlin/Heidelberg/New York 2007, ISBN 978-3-540-68411-4, S. 105 ff., doi:10.1007/978-3-540-68411-4.

[8] John W. Cahn, John E. Hilliard: Free Energy of a Nonuniform System. III. Nucleation in a Two‐Component Incompressible Fluid. In: The Journal of Chemical Physics. Band 31, Nr. 3, September 1959, ISSN 0021-9606, S. 688–699, doi:10.1063/1.1730447 (scitation.org [abgerufen am 27. Januar 2021]).

[9] K Binder: Theory of first-order phase transitions. In: Reports on Progress in Physics. 50, Nr. 7, 1. Juli 1987, ISSN 0034-4885, S. 783–859. doi:10.1088/0034-4885/50/7/001.

[10] Klaus Stierstadt: Thermodynamik (= Springer-Lehrbuch). Springer-Verlag, Berlin/Heidelberg 2010, ISBN 978-3-642-05097-8, doi:10.1007/978-3-642-05098-5. Siehe Kapitel 9, Abbildung 9.5.

[11] Bruno Predel, Michael Hoch, Monte Pool: Phase Diagrams and Heterogeneous Equilibria: a Practical Introduction. Springer-Verlag, Berlin/Heidelberg 2004, ISBN 978-3-662-09276-7, Kapitel "4 Phase Equilibria in Three-Component Systems and Four-Component Systems with Exclusion of the Gas Phase", doi:10.1007/978-3-662-09276-7.

[12] Burkhard Lohrengel: Thermische Trennverfahren: Trennung von Gas-, Dampf- und Flüssigkeitsgemischen. 3. Auflage. Walter de Gruyter, Berlin/Boston 2017, ISBN 978-3-11-047322-3, Kapitel "4.4.2 Teilweise Löslichkeit von Trägerstoff und Extraktionsmittel".