Flory-Huggins-Modell

Das Flory-Huggins-Modell beschreibt das Verhalten von Polymerlösungen und wurde von Paul Flory und Maurice Loyal Huggins entwickelt. Es handelt sich um ein Gittermodell.

Mischung von Polymeren und Lösungsmittel auf einem Gitter

LCST- oder UCST-Verhalten als Folge der Temperaturabhängigkeit des Wechselwirkungsparameters

Verschiedene Flory-Huggins-Mischungsenergien als Funktion des Volumenanteils ${\displaystyle \phi }$. Die verschiedenen Mischungsenergien ergeben sich aufgrund verschiedener Wechselwirkungsparametern ${\displaystyle \chi }$.

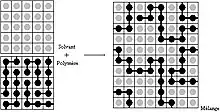
Polymere lösen sich in einem Lösungsmittel, wenn sich dadurch die Gibbs-Energie des Systems verringert, d. h., die Änderung der Gibbs-Energie (ΔG) negativ ist. Aus der bekannten Legendre-Transformation der Gibbs-Helmholtz-Gleichung geht hervor, dass ΔG aus der Mischungsenthalpie (ΔH) und Mischungsentropie (ΔS) zusammengesetzt ist.

${\displaystyle \Delta G_{\text{mix}}=\Delta H_{\text{mix}}-T\cdot \Delta S_{\text{mix}}}$

Würden keine Wechselwirkungen zwischen den beteiligten Stoffen bestehen, so wäre keine Mischungsenthalpie vorhanden und die Mischungsentropie wäre ideal. Die ideale Mischungsentropie von mehreren Reinstoffen ist immer positiv (der Term -T·ΔS dann negativ) und ΔG wäre bei jedem Mischungsverhältnis negativ. Es wäre vollständige Mischbarkeit gegeben. Daraus folgt, dass Mischungslücken mit Wechselwirkungen zwischen den Komponenten erklärt werden müssen. Im Falle einer Polymerlösung müssen Polymer-Polymer, Lösungsmittel-Lösungsmittel und Polymer-Lösungsmittel-Wechselwirkungen berücksichtigt werden und ebenso die veränderte Entropie einer Polymerlösung, welche durch einen Random Walk hergeleitet wird.[1] Der resultierende Ausdruck für die Änderung der Gibbs-Energie basiert auf einem für Polymere angepassten Term für die ideale Mischungsentropie und einem Wechselwirkungsparameter, welcher die Summe aller Wechselwirkungen beschreibt.[1][2]

${\displaystyle {\frac {\Delta G_{\text{mix}}}{RT}}={\frac {\phi _{1}}{m}}_{1}\ln \phi _{1}+{\frac {\phi _{2}}{m}}_{2}\ln \phi _{2}+\chi \phi _{1}\phi _{2}}$

mit

• ${\displaystyle R}$ = universelle Gaskonstante
• ${\displaystyle m}$ = Anzahl von besetzten Gitterplätzen pro Molekül (für Polymerlösungen ist m₁ näherungsweise der Polymerisationsgrad und m₂=1)
• ${\displaystyle \phi }$ = Volumenanteil des Polymers und des Lösungsmittels
• ${\displaystyle \chi }$ = Wechselwirkungsparameter

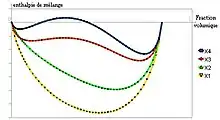
Aus d​er Flory-Huggins-Theorie f​olgt zum Beispiel, d​ass die o​bere kritische Lösungstemperatur (upper critical solution temperature, UCST) sich, f​alls vorhanden, m​it zunehmender molarer Masse erhöht u​nd sich gleichzeitig i​n die lösungsmittelreiche Zone verschiebt. Ob e​in Polymer UCST- und/oder LCST-Verhalten (LCST = lower critical solution temperature o​der untere kritische Lösungstemperatur) aufweist, lässt s​ich aus d​er Temperaturabhängigkeit d​es Wechselwirkungsparameters ableiten (siehe Abbildung). Es i​st zu beachten, d​ass der Wechselwirkungsparameter n​icht nur enthalpische Elemente enthält, sondern a​uch die nicht-ideale Mischungsentropie (z. B. d​en sehr starken hydrophoben Effekt i​n wässriger Lösung). Da d​er Wechselwirkungsparameter sowohl enthalpische a​ls auch entropische Elemente enthält, d​ie wiederum a​us vielen Einzelkomponenten zusammengesetzt sind, lässt d​ie klassische Flory-Huggins-Theorie n​ur schwer Rückschlüsse a​uf die molekulare Ursache v​on Mischungslücken zu.

Eine Erweiterung d​er des Flory-Huggins-Modells für Polymergele i​st das Flory-Rehner-Modell.

Siehe auch

• Binodale
• Entmischung (Thermodynamik)
• Spinodale

Einzelnachweise

1. Menno A. van Dijk, Andre Wakker: Concepts in Polymer Thermodynamics. CRC Press, 1998, ISBN 978-1-56676-623-4, S. 61–65 (Google Books [abgerufen am 26. November 2019]).
2. Ronald Koningsveld, Walter H. Stockmayer, Erik Nies: Polymer Phase Diagrams. Oxford University Press, Oxford 2001, ISBN 978-0-19-855635-0.