Barotropie

Unter Barotropie (von griechisch baros „Druck“ und tropos „Drehung, Richtung“) versteht man die Eigenschaft der Dichte $\rho$ eines Fluids, nur vom Druck $p$ abzuhängen: $\rho =\rho {}(p)$ . Dies führt dazu, dass Flächen gleichen Druckes (Isobaren) und gleicher Temperatur (Isothermen) parallel zueinander verlaufen. Das Gegenstück zur Barotropie ist die Baroklinität.

Die Abbildungen zeigen extrem übertriebene Neigungen, die in der Realität meist äußerst klein und daher schwer messbar sind.

Barotropie in der Atmosphäre

Barotrope Atmosphäre

In der barotropen Atmosphäre stehen die Flächen gleicher Temperatur parallel zu denen gleichen Druckes. Daher ist die mittlere Temperatur zwischen zwei Flächen gleichen Druckes überall dieselbe und ihre Neigung konstant mit der Höhe. Hieraus resultiert eine dem Betrag und der Richtung nach konstante Windgeschwindigkeit.

Barotropie im Ozean

Barotroper Ozean

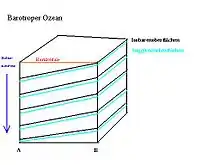
Im Ozean geht man vor allem in der als relativ homogen angenommenen Tiefenschicht von barotropen Verhältnissen aus.

Die Isopyknenoberflächen (Flächen konstanter Dichte) und die Isobarenoberflächen sind parallel zueinander gerichtet. Ihre Neigung bleibt mit zunehmender Tiefe konstant. Daher ist der horizontale Druckgradient von B nach A sowie die geostrophische Strömung konstant mit der Tiefe.

Barotropisches Phänomen

Das barotropische Phänomen (auch barotropische Inversion) tritt in Mischungen zweier Stoffe mit unterschiedlichen Molekulargewichten in bestimmten Temperatur-, Mischungs- und Druckbereichen auf, wenn bei Koexistenz von flüssiger und gasförmiger Phase die Gasphase die größere Dichte hat und unter die Flüssigkeit sinkt.[1] Das Phänomen wurde 1906 entdeckt. Heike Kamerlingh Onnes entdeckte mit Keesom, dass bei Kompression von gasförmigem Helium über flüssigem Wasserstoff das Gas bei Drücken über 30 bar und Temperaturen von rund 20 Grad Kelvin unter der Flüssigkeit gelagert war.[2]

Astrophysik

In der Astrophysik werden zum Beispiel bei theoretischen Untersuchungen des Sternaufbaus gerne polytrope Zustandsgleichungen der Form

p=K\cdot \rho ^{\gamma }

mit dem Druck p, der Dichte $\rho$ , der Polytropenkonstante K und dem Polytropenindex $\gamma =1+{\frac {1}{n}}$ verwendet,[3] was von Robert Emden für einfache Sternmodelle verwendet wurde. Für ideale nicht-relativistische Gase ist $n={\frac {3}{2}}$ , für relativistische Gase (wie dem entarteten Elektronengas in weißen Zwergen) $n=3$ . Polytropie ist in diesem Fall ein Spezialfall von Barotropie.

Barotropie in der Bodenmechanik

In der Bodenmechanik wird mit Barotropie die Abhängigkeit des Reibungswinkels vom mittleren Druckniveau bezeichnet. Dabei nimmt der Reibungswinkel mit zunehmendem mittleren Druck ab.

Das Phänomen wird in der Regel vernachlässigt und findet meist nur bei der Betrachtung niedriger Spannungszustände Anwendung.[4]

Literatur

Walter Roedel: Physik unserer Umwelt: Die Atmosphäre. Springer Verlag, Berlin 2000, ISBN 3-540-67180-3.
Gösta H. Liljequist, Konrad Cehak: Allgemeine Meteorologie. Springer-Verlag, Berlin 1984, ISBN 3-540-41565-3.
Dimitrios Kolymbas: Geotechnik – Bodenmechanik und Grundbau. Springer Verlag, Berlin 1998, ISBN 3-540-62806-1.

Einzelnachweise

Spektrum Lexikon der Physik, 1998, Band 1, S. 239
J. S. Rowlinson, James Dewar, Ashgate 2012, S. 139
Zum Beispiel Polytrop, Spektrum Lexikon Astronomie
Vgl. Dimitrios Kolymbas: Geotechnik – Bodenmechanik und Grundbau. Springer Verlag, Berlin 1998, S. 104.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Spektrum Lexikon der Physik, 1998, Band 1, S. 239

[2] J. S. Rowlinson, James Dewar, Ashgate 2012, S. 139

[3] Zum Beispiel Polytrop, Spektrum Lexikon Astronomie

[4] Vgl. Dimitrios Kolymbas: Geotechnik – Bodenmechanik und Grundbau. Springer Verlag, Berlin 1998, S. 104.