Linearität
Linearität (lateinisch linea „Linie“, linearis „aus Linien bestehend“) hat in verschiedenen Bereichen eine unterschiedliche Bedeutung, beschreibt aber zumeist eine geradlinige Beschaffenheit.
Diese Seite wird im Sinne der Richtlinien für Begriffsklärungen auf der Diskussionsseite des Wikiprojektes Begriffsklärungsseiten diskutiert. Hilf mit, die Mängel zu beseitigen, und beteilige dich an der Diskussion! Hinweise zur Überarbeitung: Formatvorlage und FAQ.
Linearität in Naturwissenschaft und Technik
Allgemeine Definition
Linearität ist die Eigenschaft eines Systems, auf die Veränderung eines Parameters stets mit einer dazu proportionalen Änderung eines anderen Parameters zu reagieren.[1]
Diese allgemeine Definition trifft gleichermaßen für Mathematik, Naturwissenschaft und Technik zu. Ist sie nicht erfüllt, so spricht man von Nichtlinearität.
Bei genauerem Hinsehen wird Linearität jedoch in verschiedenen Bedeutungen verwendet. In den folgenden Kapiteln zu Mathematik, Physik, Chemie und Technik wird Linearität gemäß dieser Definition wie im Artikel Lineare Funktion verwendet; im Kapitel zur Systemtheorie wird Linearität – enger als in vorstehender Definition – wie im Artikel Lineare Abbildung verwendet.[2] Dann werden die linearen Funktionen auf den Spezialfall der Proportionalität eingeschränkt.
Linearität in der Mathematik
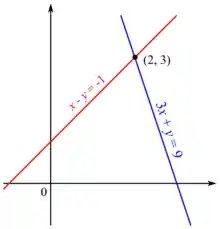
Linearität in der Mathematik lässt sich am einfachsten anhand sogenannter linearer Funktionen erklären. Dies sind spezielle Funktionen, bei denen die Abbildung einer oder mehrerer Größen auf eine andere entsprechend der allgemeinen Definition erfolgt. Linearität ist weiterhin eine Eigenschaft verschiedener mathematischer Transformationen wie z. B. der Z-Transformation oder der kontinuierlichen Fourier-Transformation.
Weiterhin trifft man bei folgenden mathematischen Themen auf den (dort teilweise verschärften) Begriff der Linearität:
- in der linearen Algebra, dem Studium von Vektorräumen
- bei einer linearen Abbildung, einer strukturerhaltenden Abbildung zwischen zwei Vektorräumen
- bei einer linearen Gleichung, einem speziellen Typ von Gleichungen, wie zum Beispiel linearen gewöhnlichen Differentialgleichungen
- bei Ordnungsrelationen im Begriff der linearen Ordnung
Siehe auch: Linearisierung (lineare Funktion als Näherung für eine nichtlineare Funktion)
Linearität bei statistischen Modellen
Die Statistik liefert Methoden, mit deren Hilfe statistische Modelle in lineare und nichtlineare Modelle unterschieden werden können. Die Besonderheit dabei: Lineare Modelle sind in den geschätzten Parametern linear, aber nicht unbedingt in den unabhängigen Variablen. Was ist damit gemeint?
Erklärung: In der Quadratischen Gleichung ist nicht die unabhängige Variable , sondern die Parameter des Modells (hier die Koeffizienten: ) ausschlaggebend für das Vorliegen von Linearität. Aufgrund dessen kann die multiple lineare Regression zur Parameterabschätzung von „gekrümmten“ Modellen verwendet werden.[3]
Linearität bei der Methodenvalidierung
Bei der Methodenvalidierung, wie sie z. B. in der analytischen Chemie oder Forensik verwendet wird, ist ein statistischer Test auf Linearität nach Mandel, der sogenannte Mandel-Test (oder Mandel-Anpassungstest) üblich, anhand dessen bestimmt wird, welches Regressionsmodell (lineare oder quadratische Regression) für den vorliegenden Untersuchungsfall anzunehmen ist.
Linearität in Physik, Chemie und Technik
Linearität in der Systemtheorie
In der interdisziplinären Systemtheorie werden lineare und nichtlineare Systeme unterschieden.
Ein System ist dann linear, wenn die beiden folgenden Kriterien erfüllt sind:
- Wenn eine Eingangsgröße zu einer Ausgangsgröße führt, wird eine Eingangsgröße von zu einer Ausgangsgröße von führen. Anders ausgedrückt, die Magnitude (Größenordnung) der Eingangsgröße ist proportional zur Magnitude der Ausgangsgröße des Systems.
- Wenn eine Eingangsgröße zu einer Ausgangsgröße führt und eine Eingangsgröße zu einer Ausgangsgröße führt, so verursacht eine Eingangsgröße eine Ausgangsgröße . Anders ausgedrückt, das System behandelt zwei simultane Eingangsgrößen voneinander unabhängig und diese interagieren innerhalb des Systems nicht miteinander.
- Implizit in diesen Kriterien ist das Faktum, dass lineare Systeme keinerlei Frequenzen am Ausgang produzieren, die nicht schon am Eingang vorhanden sind.
- Dabei ist weiterhin zu beachten, dass in diesen Kriterien keinerlei Aussage steckt, wonach die Ausgangsgröße gleich der Eingangsgröße wäre, oder dieser auch nur ähnelt. Beispielsweise könnte die Eingangsgröße ein elektrischer Strom sein und die Ausgangsgröße eine Temperatur. Im Falle mechanischer Strukturen wie z. B. Maschinen könnte man eine schwingende Kraft als Eingangsgröße und eine messbare Schwingung (Bewegung) als Ausgangsgröße vorstellen.[1]
Weiterhin kennt die Systemtheorie auch noch lineare, zeitinvariante, dynamische Systeme.
Linearität in der Ethnosoziologie
Die Ethnosoziologie verwendet die Bezeichnung „Linearität“, um zwischen linearer Verwandtschaft und kollateraler Seitenverwandtschaft zu unterscheiden: Linearität bezeichnet dabei die direkte Abstammung von Eltern, deren Eltern und so weiter, sowie die gesamte eigene Nachkommenschaft (gerade Linie), während Kollateralität die indirekte Verwandtschaft zwischen Geschwistern aller Generationen und deren Nachkommen bezeichnet (Seitenlinie).
Die Linearität von Verwandtschaft spielt eine wichtige Rolle bei unilinearen Abstammungsregeln, die eine einlinige Erbnachfolge festlegen:
- Patri-Linearität: nur über die Väterlinie (46 Prozent der weltweit 1300 Ethnien und indigenen Völker)
- Matri-Linearität: nur über die Mütterlinie (13 Prozent)
- Bi-Linearität: doppelt, über beide Linien, je eine nach sozialem Zusammenhang (4 Prozent)
- Ambi-Linearität: eine selbst gewählte, von der Mutter oder vom Vater übernommene gemischte Linie (4 Prozent)
- Parallele Linearität: die Mutter überträgt ihre Linie an Töchter, der Vater seine an Söhne (1 Prozent)
Linearität in der Geschichtsphilosophie
Die Geschichtsphilosophie unterscheidet verschiedene Ansätze zur Interpretation des geschichtlichen Verlaufs, darunter lineare Modelle, die von einem Anfang und einem Ende der Geschichte ausgehen. Zyklische Theorien hingegen legen der Geschichte ein Kreis- oder Spiralmodell zugrunde, während biologistische Ansätze die Entwicklung einzelner Gesellschaften in Analogie zu den verschiedenen Lebensaltern interpretieren. Das offene Modell schließlich interpretiert Geschichte als einen wesentlich undeterminierten Vorgang, der aufgrund seiner Komplexität nicht oder nur in kurzfristigen und klar umrissenen Kontexten vorherbestimmt werden kann.[4]
Linearität von Texten und Medien
Linearität von Texten beispielsweise in Büchern liegt vor, wenn diese in einer bestimmten, linearen Reihenfolge geschrieben und gelesen werden. Ausprägungen von Linearität bei Texten können sein:
- von Seite zu Seite, oder von Blatt zu Blatt
- von vorne nach hinten, oder von hinten nach vorne
- von Zeile zu Zeile, oder von Spalte zu Spalte
- von links nach rechts, oder von rechts nach links
- von oben nach unten, oder von unten nach oben
Dieser Linearität des Textes folgt die Bewegungsrichtung der Augen des Autors oder Lesers.
Moderne Medien wie das Internet erlauben mit Hilfe von Hypertext diese Linearität in bestimmten Bereichen aufzubrechen, indem Texte untereinander verlinkt werden und diesen so eine nichtlineare Komponente hinzugefügt wird. Die Linearität einzelner Abschnitte bleibt dabei zwar erhalten, der Leser bestimmt jedoch die Leserichtung durch Auswahl der ihn interessierenden Inhalte anhand der von Autoren gesetzten Hyperlinks und bewegt sich so nichtlinear durch die vorhandenen Medieninhalte.[5] Diese Non-Linearität von Hypertext gilt als wesentliches Element der Hypertext-Theorie.[6]
Linearität in der Musik
In der Musik bezeichnet Linearität ein Verhältnis einer, zweier oder mehrerer Stimmen zueinander im Verhältnis zu den jeweiligen Regeln des Tonsatzes. Dass dies schon mit der Einstimmigkeit beginnt, liegt daran, dass auch dort schon festgelegte Wendungen, sogenannte (Schluss-)Klauseln eingehalten werden, oder eben nicht.
Siehe auch
- Lineartechnik (Antriebstechnik)
- Methode der globalen Linearisierung (Regelungstheorie)
- LINEAR: Lincoln Near Earth Asteroid Research
- Linearität der geschichtlichen Veränderung
- David R. Hawkins: Nicht-Dualität und Nicht-Linearität
- Linear-Antiqua (Schriftarten)
Einzelnachweise
- Eintrag: [https://de.wikipedia.org/w/index.php?title=Wikipedia:Defekte_Weblinks&dwl=http://www.dliengineering.com/vibman/definitionoflinearity.htm Seite nicht mehr abrufbar], Suche in Webarchiven: [http://timetravel.mementoweb.org/list/2010/http://www.dliengineering.com/vibman/definitionoflinearity.htm Definition of Linearity.] In: Azima DLI. USA 2009, abgerufen am 22. Dezember 2013 (englisch; Definition von Linearität bei Systemen).
- Hans Humenberger, Berthold Schuppar: Mit Funktionen Zusammenhänge und Veränderungen beschreiben. Springer, 2019, S. 29.
- Hans Lohninger: Lineare und nicht lineare Modelle. In: Grundlagen der Statistik. Eigene Webseite, Oktober 2012, abgerufen am 22. Dezember 2013.
- Zu einer kritischen Übersicht über diese verschiedenen Strukturmodelle vgl. David Engels, Biologistische und zyklische Geschichtsphilosophie. Ein struktureller Annäherungsversuch, in: ders. (Hg.), Von Platon bis Fukuyama. Biologistische und zyklische Konzepte in der Geschichtsphilosophie der Antike und des Abendlandes, Brüssel 2015, 8–46.
- Stefan Münz: Hypertext (1): Text und Linearität. In: Webkompetenz-Blog. 29. März 2007, abgerufen am 22. Dezember 2013.
- Non-Linearität. In: HistnetWiki. 21. März 2006, abgerufen am 22. Dezember 2013 (Non-Linearität in der Hypertext-Theorie).