Strömungsmechanik

Die Strömungsmechanik, Fluidmechanik oder Strömungslehre ist die Wissenschaft vom physikalischen Verhalten von Fluiden. Die in der Strömungsmechanik gewonnenen Kenntnisse sind Gesetzmäßigkeiten in Strömungsvorgängen und dienen der Lösung von Strömungsproblemen in der Auslegung von durch- bzw. umströmten Bauteilen sowie der Überwachung von Strömungen. Angewendet wird sie unter anderem im Maschinenbau, Chemieingenieurwesen, der Wasser- und Energiewirtschaft, Meteorologie, Astrophysik und der Medizin. Ihre Grundlagen findet sie in der Kontinuumsmechanik und Thermodynamik, also der klassischen Physik.

Historische Entwicklung

Die Strömungsmechanik beruht auf der Kontinuumsmechanik, Physik und Differentialrechnung, deren jeweiliger historischer Werdegang dort nachgeschlagen werden kann. An dieser Stelle soll die spezifisch strömungsmechanische Entwicklung skizziert werden.

Archimedes (287–212 v. Chr.) befasste sich mit strömungsmechanischen Fragestellungen (Archimedisches Prinzip, Archimedische Schraube). Sextus Iulius Frontinus (ca. 35–103 n. Chr.) dokumentierte seine Kenntnisse über die Wasserversorgung in der Antike, über tausend Jahre bevor sich Leonardo da Vinci (1452–1519) mit Strömungsvorgängen auseinandersetzte.

Galileo Galilei (1564–1642) gab Impulse in der experimentellen Hydrodynamik und überarbeitete das von Aristoteles eingeführte Konzept des Vakuums. Evangelista Torricelli (1608–1647) erkannte im Gewicht der Erdatmosphäre die Ursache des Luftdrucks und verband den horizontal ausgestoßenen Flüssigkeitsstrahl mit den Gesetzen des freien Falls (Torricelli’sches Ausflussgesetz). Blaise Pascal (1623–1662) beschäftigte sich unter anderem mit der Hydrostatik und formulierte den Satz von der allseitigen Druckfortpflanzung. Edme Mariotte (1620–1684) lieferte Beiträge zu Problemen der Flüssigkeiten und Gase und stellte dabei erste Konstitutivgesetze auf. Henri de Pitot (1695–1771) untersuchte den Staudruck in Strömungen.

Isaac Newton veröffentlichte 1686 seine dreibändige Principia mit den Bewegungsgesetzen und definierte zudem im zweiten Buch die Viskosität einer idealen (newtonschen) Flüssigkeit. Daniel Bernoulli (1700–1782) begründete die Hydromechanik, indem er Druck und Geschwindigkeit in der nach ihm benannten Energiegleichung verband und Leonhard Euler (1707–1783) formulierte die Bewegungsgleichungen für ideale Flüssigkeiten. Von nun an konnten Erkenntnisse auch durch Untersuchungen der mathematischen Gleichungen gewonnen werden. Jean-Baptiste le Rond d’Alembert (1717–1783) führte die eulersche Betrachtungsweise und komplexe Zahlen in der Potentialtheorie ein, leitete die lokale Massenbilanz her und formulierte das d’Alembert’sche Paradoxon, demgemäß von der Strömung idealer Flüssigkeiten auf einen Körper keine Kraft in Richtung der Strömung ausgeübt wird (was Euler schon vorher bewies). Wegen dieser und anderer Paradoxien reibungsfreier Strömungen war klar, dass die Euler’schen Bewegungsgleichungen zu ergänzen sind.

Claude Louis Marie Henri Navier (1785–1836) und George Gabriel Stokes (1819–1903) erweiterten die Euler’schen Bewegungsgleichungen um viskose Terme zu den Navier-Stokes-Gleichungen, die Strömungen realitätsnah modellieren. Giovanni Battista Venturi (1746–1822), Gotthilf Heinrich Ludwig Hagen (1797–1884) und Jean Léonard Marie Poiseuille (1799–1869) führten experimentelle Untersuchungen in Strömungen durch. William Froude (1810–1879) ermittelte den Schwimmwiderstand von Schiffen, Ernst Mach (1838–1916) leistete Pionierarbeit in der Überschallaerodynamik, Lord Rayleigh (1842–1919) untersuchte hydrodynamische Instabilitäten und Vincent Strouhal (1850–1922) erforschte die Schwingungsanregungen durch ablösende Wirbel. Hermann von Helmholtz (1821–1894) formulierte die nach ihm benannten Wirbelsätze und begründete durch mathematisch ausgearbeitete Untersuchungen über Wirbelstürme und Gewitter die wissenschaftliche Meteorologie. Weitere bahnbrechende Arbeiten wurden von Osborne Reynolds (1832–1912, Reynolds-Gleichungen, Reynoldszahl) und Ludwig Prandtl (1875–1953, unter anderem zur hydrodynamischen Grenzschicht) vorgelegt.

Andrei Nikolajewitsch Kolmogorow (1903–1987) erweiterte die Theorie der turbulenten Strömung. Ab Mitte des 20. Jahrhunderts entwickelten sich die Strömungsmesstechnik und numerische Strömungsmechanik so weit, dass mit ihrer Hilfe Lösungen für praktische Probleme gefunden werden können.[1]

Methodik

Gegenstand der Strömungsmechanik sind die Bewegungen von Fluiden, ruhenden, fließenden oder strömenden Medien. Die Suche nach Gesetzmäßigkeiten von Bewegungen und Lösungen für Strömungsprobleme bedient sich dreierlei Methoden:

Analytische Methoden: Gesetzmäßigkeiten werden in Form von Gleichungen formuliert, die mit Hilfe der angewandten Mathematik behandelt werden können.
Experimentelle Methoden: Die Phänomenologie der Strömungsvorgänge wird erkundet mit dem Ziel Gesetzmäßigkeiten herauszufinden.
Numerische Methoden: Durch einen detaillierten Einblick auch in komplizierte und kurzzeitige Strömungsvorgänge unterstützen und ergänzen die Berechnungen die analytischen und experimentellen Methoden.

Die Komplexität des Gegenstandes macht die kombinierte Nutzung aller drei Methoden für die Lösung praktischer Strömungsprobleme notwendig.

Teilgebiete

Fluidstatik

Hydrostatisches Paradoxon: Der Flüssigkeitsdruck am Boden (rot) ist in allen drei Gefäßen identisch.

Die Fluidstatik betrachtet ruhende Fluide, wobei die Hydrostatik Inkompressibilität voraussetzt, die Wasser in guter Näherung aufweist. Hier interessiert die Druckverteilung in ruhenden Flüssigkeiten und die daraus resultierenden Kräfte auf Behälterwände, siehe Bild. Schwimmende Körper erfahren einen statischen Auftrieb und es interessiert die Frage, unter welchen Voraussetzungen die Schwimmstabilität des Körpers gegeben ist. Thermische Effekte sind hier von untergeordneter Bedeutung.

Die Aerostatik betrachtet die Gesetzmäßigkeiten in ruhender Atmosphäre oder Erdatmosphäre und hier sind Dichteänderungen und thermische Effekte ausschlaggebend. Betrachtet wird beispielsweise die Atmosphärenschichtung und die Druck- und Temperaturverteilung über die Höhe in der Erdatmosphäre.

Ähnlichkeitstheorie

Windkanal der NASA mit dem Modell einer MD-11

Die Ähnlichkeitstheorie beschäftigt sich damit, aus einem bekannten und zugänglichen (Modell)-System Rückschlüsse auf ein interessierendes aber experimentell unzugängliches (Real)-System zu bilden, das z. B. größer oder kleiner, schneller oder langsamer oder sich in anderen Dimensionen nur quantitativ vom Modellsystem unterscheidet, siehe Bild. Kinematisch ähnlich sind zwei Strömungen, wenn sie ähnliche räumliche Bewegungen ausführen. Voraussetzung hierfür ist, dass ähnliche Randbedingungen vorliegen (geometrische Ähnlichkeit) und auf die Fluidelemente ähnliche Kräfte wirken, was dynamische Ähnlichkeit bedeutet. Die Ähnlichkeitsbetrachtungen werden auch auf Wärmetransportprobleme bei thermischer Ähnlichkeit angewendet. Begründet wurde die Ähnlichkeitstheorie 1883 von Osborne Reynolds in Form des Reynolds’schen Ähnlichkeitsgesetzes, das besagt, dass die Strömungen am Original und am Modell mechanisch ähnlich verlaufen, wenn die Reynolds-Zahlen übereinstimmen.

Stromfadentheorie

Die Stromfadentheorie betrachtet Strömungen entlang einer von Stromlinien gebildeten, (infinitesimal) dünnen Stromröhre, in der die Zustandsgrößen Geschwindigkeit, Druck, Dichte und Temperatur als über den Querschnitt des Stromfadens konstant angenommen werden können. Auf diese Volumina können die Integralformen der Grundgleichungen angewendet werden, um so weitere Lösungen von Strömungsproblemen zu erarbeiten. Ein stationäres Strömungsgebiet besteht aus Stromfäden, so dass es gelingt die globalen Eigenschaften der Strömung mit den Eigenschaften der Stromfäden zu beschreiben. Prominenter Anwendungsfall ist die Strömung durch Röhren und Düsen. Die Gesamtheit der eindimensionalen Strömungen von Wasser werden unter dem Sammelnamen Hydraulik zusammengefasst.[2] Die Fluidtechnik und Fluidik wenden die Hydraulik und Pneumatik an, um Energie zu übertragen oder Signale zu verarbeiten.

Potentialströmungen

Stromlinien um ein Flügelprofil

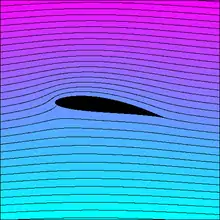
In Potentialströmungen ergibt sich das Geschwindigkeitsfeld aus der Ableitung eines Geschwindigkeitspotentials, weshalb solche Strömungen grundsätzlich reibungs- und rotationsfrei sind. Eine laminare Strömung bei niedrigen Reynolds-Zahlen folgt in guter Näherung einer Potentialströmung, wenn die fluiddynamische Grenzschicht an den Rändern der Strömung keine wesentliche Rolle spielt. Die Potentialtheorie findet Anwendung in der Auslegung und im Design von Flugzeugen. Potentialströmungen sind relativ einfach zu berechnen und erlauben analytische Lösungen für viele Strömungsprobleme.

Eine andere Idealisierung, die Rotation erlaubt, aber nur inkompressible Medien betrachtet, gestattet die Einführung einer Stromfunktion. Diese ist allerdings nur in ebenen oder als Stokessche Stromfunktion in drei dimensionalen, axialsymmetrischen Fällen anwendbar. Die Höhenlinien der Stromfunktionen sind Stromlinien.

In ebenen, dichtebeständigen und rotationsfreien Strömungen kann das Geschwindigkeitsfeld mit komplexen Funktionen ausgedrückt und somit deren weitreichenden Eigenschaften ausgenutzt werden. Mit Hilfe dieser Theorie konnten Anfang des 20. Jahrhunderts erste auftriebserzeugende Flügelprofile entwickelt werden, siehe Bild.

Gasdynamik

Der Gegenstand der Gasdynamik sind schnelle Strömungen dichteveränderlicher Fluide, die bei Flugzeugen und in Düsen vorkommen. Diese Strömungen werden durch die Mach-Zahl M charakterisiert. Kompressibilität wird erst ab Machzahlen größer 0,2 bedeutsam, so dass dann hohe Reynolds-Zahlen vorliegen und Viskositätsterme und Gravitionskräfte vernachlässigbar sind. Die Strömungen sind auch schneller als der Wärmetransport, weswegen adiabatische Zustandsänderungen angenommen werden können. Die Gesetzmäßigkeiten werden mit der Stromfaden- und Ähnlichkeitstheorie abgeleitet. Ein besonderes Phänomen, das hier auftreten kann, ist die Stoßwelle und der Verdichtungsstoß, dessen bekanntester Vertreter die Schallmauer ist.

Fluiddynamik

Stokes’sche Welle mit Bahnlinien (türkis) einiger Wasserteilchen

Die Fluiddynamik ist das Teilgebiet, das sich mit bewegten Fluiden beschäftigt. Analytische Lösungen können hier nur durch Beschränkung auf eine oder zwei Dimensionen, auf Inkompressibilität, einfache Randbedingungen und auf kleine Reynolds-Zahlen erreicht werden, wo die Beschleunigungsterme gegenüber den Viskositätstermen vernachlässigt werden können. Zwar sind solche Lösungen praktisch wenig relevant, vertiefen jedoch trotzdem das Verständnis von Strömungsvorgängen.

Bei kleinen Reynoldszahlen vermag die Viskosität des Fluids kleine Fluktuationen der Strömungsvariablen zu dämpfen, so dass eine eventuell auch zeitabhängige, laminare Strömung dann stabil gegenüber kleinen Störungen ist. Mit zunehmender Reynolds-Zahl wird dieser Dämpfungsmechanismus überfordert und die laminare Strömung geht in eine irreguläre turbulente Strömung über. Die Turbulenzforschung erreicht Einsichten über solche Strömungen durch statistische Betrachtungen.

Bei großen Reynoldszahlen sind umgekehrt die Viskositätsterme gegenüber den Beschleunigungstermen klein und der Einfluss der Randbedingungen auf die Strömung ist auf wandnahe Bereiche beschränkt. Mit diesen beschäftigt sich die von Ludwig Prandtl begründete Grenzschichttheorie.

Die Aerodynamik untersucht das Verhalten von Körpern in kompressiblen Fluiden (zum Beispiel Luft) und ermittelt Kräfte und Momente, die auf umströmte Körper wirken. Zur Aerodynamik gehört die Vorhersage der Windkräfte auf Gebäude, Kraftfahrzeuge und Schiffe.

Das Wissensgebiet um die Wellenbewegungen in Fluiden befasst sich mit zeitlichen und räumlichen Bewegungen eines Fluids um eine mittlere Ruhelage. Die Aeroakustik beschäftigt sich mit den Gesetzmäßigkeiten solcher Wellen – Schallwellen – in der Luft. Die Hydromechanik unterscheidet u. a. die Schwerewellen, die höheren Stokes-Wellen, siehe Bild, die kleinen Kapillarwellen und die aperiodischen Solitonen. In der Fluiddynamik werden die Ursachen, Eigenschaften und die Grundgleichungen dieser Wellenbewegungen untersucht.

Mehrphasenströmungen mit festen, flüssigen und/oder gasförmigen Anteilen sind die in der Natur und Technik am häufigsten auftretenden Strömungsformen und bekommen dadurch eine besondere Relevanz. Die Mischung kann einerseits bereits im Kontinuumsmodell dargestellt werden, so dass die Mischung in jedem Fluidelement vorliegt, was Vorteile bei der Betrachtung großskaliger Bewegungen hat. Andererseits kann die Strömung jeder Phase getrennt beschrieben werden und die Gesamtströmung ergibt sich dann aus der Interaktion der Phasen an ihren Grenzflächen. Hier stehen kleinskalige Effekte im Vordergrund.

Sickerströmungen durch poröse Medien sind in der Hydrogeologie und der Filtertechnik von Interesse. Die Oberflächenspannung, die sonst bei Strömungen von untergeordneter Bedeutung ist, ist hier für die Bewegung bestimmend. Weil der Porenverlauf der festen Phase unbekannt ist, kommen Modelle zum Einsatz, die in die Richards-Gleichung münden.

Lineare Stabilitätstheorie

Kelvin-Helmholtz-Wirbel in der Atmosphäre hinter dem Monte Duval, Australien

Dieses Fachgebiet untersucht, inwieweit der Bewegungszustand einer Flüssigkeit stabil ist gegenüber kleinen Störungen. Betrachtet wird die Strömung an einer Grenzschicht, die zu einer Wand (Hydrodynamische Grenzschicht) oder zu einer Flüssigkeit mit anderen Eigenschaften liegen kann. Fluktuationen in dieser Grenzschicht können bei Instabilitäten zu qualitativ anderen Zuständen führen, die oftmals deutliche Strukturen aufweisen (siehe Kelvin-Helmholtz-Instabilität im Bild).

Strömungsmesstechnik

2D-Laser-Doppler-Anemometer an einem Strömungskanal

Einsatzgebiete der Strömungsmesstechnik sind die Forschung und Entwicklung, wo es gilt, Strömungsvorgänge zu untersuchen oder zu optimieren. Die Strömungsmesstechnik ist aber auch eine wesentliche Komponente für die Prozessführung in industriellen Anlagen der Chemie- oder Energiewirtschaft. Verlässliche Informationen über Eigenschaften turbulenter Strömungen können nur durch die Strömungsmesstechnik erhalten werden.

Von besonderem Interesse sind die grundlegenden Größen Geschwindigkeit, Druck und Temperatur. Messungen können mit in die Strömung eingebrachten Messsonden aufgenommen werden. Staudrucksonden messen im Fluid den Gesamtdruck, aus dem indirekt auf die Geschwindigkeit rückgeschlossen werden kann. Die Thermische Anemometrie stellt eine weitere indirekte Geschwindigkeitsmessmethode dar. Der Nachteil an diesen indirekten Messungmethoden ist, dass das Messsignal nicht allein von der Geschwindigkeit, sondern auch von anderen Zustandsgrößen abhängt, die also bekannt sein müssen.

Verfahren wie die Particle Image Velocimetry und Laser-Doppler-Anemometrie (siehe Bild) gestattet die direkte und lokale Geschwindigkeitsmessung ohne Sonden. Insbesondere in der Aeroakustik interessieren nicht die Durchschnittswerte, sondern die Schwankungswerte des Drucks, insbesondere die spektrale Leistungsdichte, die durch weitere Signalverarbeitung erhalten wird.

Numerische Strömungsmechanik

Visualisierung einer CFD-Simulation der Boeing X-43 bei Mach 7

Die Leistungsfähigkeit der Computer gestattet es, die Grundgleichungen in wirklichkeitsnahen Randwertproblemen zu lösen und die erzielten, realitätsnahen Resultate haben dazu geführt, dass die numerische Strömungsmechanik ein wichtiges Werkzeug in der Strömungsmechanik wurde. In der aerodynamischen Auslegung und Optimierung haben sich die numerischen Methoden etabliert, denn sie gestatten einen detaillierten Einblick in die Strömungsvorgänge, siehe Bild, und Untersuchung von Modellvarianten.

Die aus der angewandten Mathematik bekannten Methoden zur Lösung gewöhnlicher Differentialgleichungen versehen vorbereitend das Strömungsgebiet mit einem „numerischen Gitter“. Potentialströmungen verlangen den geringsten Aufwand und auch die Euler-Gleichungen erlauben relativ grobe Gitter. Die bei Anwendung der Navier-Stokes-Gleichungen bedeutsamen Grenzschichten und Turbulenzen erfordern eine hohe räumliche Auflösung des Gitters. In drei Dimensionen steigt die Anzahl der Freiheitsgrade mit der dritten Potenz der Abmessung, so dass auch noch im 21. Jahrhundert der Aufwand für die Direkte Numerische Simulation bei Anwendungen in der Fahrzeugentwicklung nicht vertretbar ist. Daher kommen Turbulenzmodelle zum Einsatz, die die notwendige Auflösung zu reduzieren gestatten. Trotzdem sind oftmals Systeme mit mehreren zehnmillionen Gleichungen für mehrere tausend Iterations- oder Zeitschritte zu lösen, was eines Rechnerverbunds und effizienter Programmierung bedarf.

Interdisziplinäre Arbeitsgebiete

Rheologie

Die Rheologie oder Fließkunde ist eine interdisziplinäre Wissenschaft, die sich mit dem Verformungs- und Fließverhalten von Materie beschäftigt, und berührt daher auch die Strömungsmechanik. Die phänomenologische Rheologie befasst sich mit der Formulierung von Materialmodellen, die Strukturrheologie trachtet danach, das makroskopische Materialverhalten aus der mikroskopischen Struktur der Stoffe zu erklären, und die Rheometrie stellt Messverfahren zur Bestimmung der rheologischen Eigenschaften, z. B. der Viskosität, bereit.

Fluidenergiemaschinen

Eine mit dem Maschinenbau zusammen arbeitende Disziplin sucht mit Integralformen der Grundgleichungen makroskopische Größen der Strömungen abzuleiten, wie Volumenströme, Kräfte, Arbeiten und Leistungen. Diese Größen sind in Ingenieursproblemen in Fluidenergiemaschinen von besonderem Interesse. Eine der ersten Resultate auf diesem Gebiet formulierte Leonhard Euler in der nach ihm benannten Euler’schen Turbinengleichung.

Mikrofluidik

Ein chemischer Mikroreaktor

Die Mikrofluidik ist das Teilgebiet der Mikrosystemtechnik, das die Umströmung von Objekten oder Durchströmungen von Kanälen, bei Abmessungen kleiner als ein Millimeter, untersucht, siehe Bild. Die kontinuumsmechanische Behandlung von Strömungs- und Transportprozessen auf dieser Längenskala ist in vielen Fällen nicht ohne weiteres möglich. Es werden Korrekturen an den Gleichungen oder gar Molekulardynamik-Simulationen notwendig, um die Strömungsvorgänge korrekt wiederzugeben. Prominenter Anwendungsfall ist der Druckkopf eines Tintenstrahldruckers. Aber auch der Aufbau eines vollständigen Analyselabors auf einem Chip (englisch Lab-on-a-chip für „Labor auf einem Chip“ oder micro-total-analysis system für „Mikro-vollständiges-Analyse-System“) erfordert die Kenntnis der Strömungs- und Transportprozesse auf der Mikroskala.[3]

Bioströmungsmechanik

Die Bioströmungsmechanik befasst sich mit der Innen- und Umströmung von belebten Körpern, deren charakteristisches Merkmal unter anderem ist, von flexiblen und strukturierten Oberflächen berandet zu sein. Es wird die Fortbewegung von Einzellern, Kaulquappen und Fischen bis hin zu Walen im Wasser untersucht. Bei der Fortbewegung durch die Luft wird insbesondere der Vogelflug ergründet. Der Wärme- und Stofftransport in Lebewesen bei der Atmung, im Blut- und Lymphkreislauf und der Wasserkreislauf sind auch in der Medizin von Interesse.[4]

Magnetohydrodynamik

Die Magnetohydrodynamik (MHD) berücksichtigt die elektrischen und magnetischen Eigenschaften von Flüssigkeiten, Gasen und Plasmen und untersucht zusätzlich die Bewegung unter Wirkung der vom Medium selbst erzeugten Felder und die Bewegung in äußeren Feldern. Die Bewegungsgleichungen sind die um elektrodynamische Kräfte erweiterten Euler-Gleichungen, deren Lösung sehr kompliziert werden kann. Durch weitere Annahmen können die Gleichungen jedoch vereinfacht werden, um ihre Lösung zu erleichtern. Die Annahme, dass die elektrische Leitfähigkeit des Plasmas unendlich groß ist, es daher also keinen elektrischen Widerstand besitzt, führt auf die „Ideale MHD“ im Gegensatz zur „resistiven MHD“ mit endlicher Leitfähigkeit. Typische Anwendungsgebiete der Magnetohydrodynamik sind die Strömungsbeeinflussung und die Strömungsmessung in Metallurgie und Halbleiter-Einkristallzüchtung sowie die Beschreibung von Plasmen in stellaren Atmosphären und Fusionsreaktoren.[5]

Kontinuumsmechanische Grundlagen

Strömungen können aus den Augen der statistischen Mechanik als Partikelströme oder als Kontinuumsströmungen betrachtet werden. Letzterer Ansatz kommt aus der Kontinuumsmechanik,[6] in der vom molekularen Aufbau der Fluide abgesehen wird und sie als Kontinuum angenähert werden, in dem die physikalischen Eigenschaften kontinuierlich über den Raum verschmiert sind. Dieser phänomenologische Ansatz erlaubt effizient realitätsnahe Vorhersagen zu formulieren. Die für die Strömungsmechanik relevanten kinematischen, physikalischen und konstitutiven kontinuumsmechanischen Gleichungen werden im Folgenden zusammengefasst.

Kinematik

Die Strömungsmechanik benutzt die eulersche Betrachtungsweise, die die an einem festen Raumpunkt vorhandenen physikalischen Größen untersucht. Weil sich die physikalischen Gesetze auf materielle Punkte (hier: Fluidelemente) und nicht auf Raumpunkte beziehen, muss bei der Zeitableitung die substantielle Ableitung benutzt werden. Diese besteht aus einem lokalen und einem konvektiven Anteil:

{\dot {f}}:={\frac {\mathrm {D} f}{\mathrm {D} t}}:={\frac {\partial f}{\partial t}}+\operatorname {grad} (f)\cdot {\vec {v}}={\frac {\partial f}{\partial t}}+({\vec {v}}\cdot \nabla )f\,.

Das vom Fluid transportierte Feld f kann skalar- oder vektorwertig sein und hängt wie die Geschwindigkeit vom Ort und der Zeit ab. Die partielle Ableitung ${\tfrac {\partial f}{\partial t}}$ ist die lokale Ableitung, d. h. die an einem festen Raumpunkt zu beobachtende Änderungsgeschwindigkeit, und der zweite Term mit dem Gradienten grad oder dem Nabla-Operator $\nabla$ ist der konvektive Anteil. Im Fall einer vektoriellen Größe ${\vec {f}}$ wird in der Strömungsmechanik die Schreibweise mit dem Vektorgradient $({\vec {v}}\cdot \nabla ){\vec {f}}$ bevorzugt.

In der Strömungsmechanik ist die Geschwindigkeit ${\vec {v}}$ die primäre Unbekannte und ihr Gradient, der Geschwindigkeitsgradient

\mathbf {l

ist eine zentrale Größe bei der Beschreibung von Strömungsvorgängen. Die Geschwindigkeitskomponenten $v_{x,y,z}$ beziehen sich auf ein kartesisches Koordinatensystem mit x-, y- und z-Koordinaten. Für ein Fluidelement mit (infinitesimal) kleinem Volumen dv ergibt sich die Volumenänderungsgeschwindigkeit

{\frac {\mathrm {D} }{\mathrm {D} t}}(\mathrm {d} v)=\operatorname {Sp} (\mathbf {l} )\,\mathrm {d} v\,.

Die Spur Sp des Geschwindigkeitsgradienten ist somit ein Maß für die Volumenänderungsgeschwindigkeit, die auf Grund der Massenbilanz unten mit einer Dichteänderung einher geht. Die Spur ist gleich der Divergenz div des Geschwindigkeitsfeldes: $\operatorname {Sp} (\mathbf {l} )=\operatorname {div} ({\vec {v}})\,.$ Der Geschwindigkeitsgradient kann additiv in einen symmetrischen Anteil d und einen schiefsymmetrischen Anteil w zerlegt werden:

\mathbf {l} =\mathbf {d+w} \quad {\text{mit}}\quad \mathbf {d

Das Superskript $\top$ bezeichnet die Transposition. Der symmetrische Anteil d ist der Verzerrungsgeschwindigkeitstensor, mit dem sich mit

{\dot {\varepsilon }}_{1}:={\hat {e}}_{1}\cdot \mathbf {d} \cdot {\hat {e}}_{1}\quad {\text{und}}\quad {\dot {\gamma }}_{12}:=2{\hat {e}}_{1}\cdot \mathbf {d} \cdot {\hat {e}}_{2}

die Dehnungsgeschwindigkeit ${\dot {\varepsilon }}_{1}$ in ${\hat {e}}_{1}$ -Richtung und die Schergeschwindigkeit ${\dot {\gamma }}_{12}$ in der 1-2-Ebene berechnet, die von zueinander senkrechten Einheitsvektoren (mit der Länge eins) ${\hat {e}}_{1,2}$ aufgespannt wird. Der schiefsymmetrische Anteil w ist der Wirbeltensor, dem über

\mathbf {w} \cdot {\vec {u}}=:{\vec {\Omega }}\times {\vec {u}}\quad \forall {\vec {u}}

ein Vektor ${\vec {\Omega }}$ zugeordnet werden kann, der im Fall des Wirbeltensors Winkelgeschwindigkeit genannt wird und die Drehgeschwindigkeit der Fluidelemente um sich selbst angibt. Nach obiger Definition berechnet sich

{\vec {\Omega }}={\frac {1}{2}}\operatorname {rot} {\vec {v}}\,.

Die Rotation rot des Geschwindigkeitsfeldes wird als Wirbelstärke oder Wirbelvektor bezeichnet:

{\vec {\omega }}:=\operatorname {rot} {\vec {v}}=2{\vec {\Omega }}\,.

Gelegentlich wird auch ${\vec {\omega }}={\tfrac {1}{2}}\operatorname {rot} {\vec {v}}$ definiert, was keinen wesentlichen Unterschied ausmacht.

Naturgesetze

Die Kontinuumsmechanik formuliert die folgenden, an jedem Fluidelement geltenden Naturgesetze:

Massenbilanz: ${\frac {\partial }{\partial t}}\rho +\operatorname {div} (\rho {\vec {v}})={\frac {\partial \rho }{\partial t}}+\operatorname {grad} (\rho )\cdot {\vec {v}}+\rho \,\operatorname {div} ({\vec {v}})={\dot {\rho }}+\rho \operatorname {div} ({\vec {v}})=0$
Impulsbilanz: $\rho {\dot {\vec {v}}}=\rho \left[{\frac {\partial }{\partial t}}{\vec {v}}+\operatorname {grad} ({\vec {v}})\cdot {\vec {v}}\right]=\rho \left[{\frac {\partial }{\partial t}}{\vec {v}}+({\vec {v}}\cdot \nabla ){\vec {v}}\right]=\rho \,{\vec {k}}+\operatorname {div} ({\boldsymbol {\sigma }})\,,$ und
Energiebilanz: ${\dot {u}}={\frac {1}{\rho }}{\boldsymbol {\sigma }}:\mathbf {d} -{\frac {1}{\rho }}\operatorname {div} \;{\vec {q}}+r\,.$

Darin sind ρ die Dichte, ${\vec {k}}$ eine Schwerebeschleunigung, ${\boldsymbol {\sigma }}$ der Cauchy’sche Spannungstensor, u die innere Energie, ${\vec {q}}$ der Wärmestrom, $r$ innere Wärmequellen z. B. aus Phasenübergängen, „ $\cdot$ “ das Frobenius-Skalarprodukt von Vektoren und „:“ dasjenige von Tensoren. Die Drehimpulsbilanz reduziert sich auf die Forderung nach der Symmetrie des Spannungstensors $({\boldsymbol {\sigma }}={\boldsymbol {\sigma }}^{\top })\,.$

Materialmodelle

Abgeschlossen wird das System aus kinematischen und Bilanzgleichungen durch ein Materialmodell des Fluids, das den Spannungstensor in Abhängigkeit von dem Verzerrungsgeschwindigkeitstensor, der Dichte oder weiteren Konstitutivvariablen spezifiziert. Das Materialmodell der klassischen Materialtheorie für das linear viskose oder newtonsche Fluid

{\boldsymbol {\sigma }}=-p(\rho )\mathbf {I} +2\mu \mathbf {d} +\lambda \operatorname {Sp} (\mathbf {d} )\mathbf {I}

ist das, in der Strömungsmechanik hauptsächlich benutzte Materialmodell. Darin sind p der im Allgemeinen von der Dichte ρ abhängige Druck, λ und μ die ersten und zweiten Lamé-Konstanten und I der Einheitstensor. Der Verzerrungsgeschwindigkeitstensor ist im Allgemeinen voll besetzt und dann treten geschwindigkeitsabhängige Schubspannungen auf, die sich makroskopisch als Viskosität bemerkbar machen. In Kombination mit der Impulsbilanz liefert dieses Modell die Navier-Stokes-Gleichungen. Weil der Druck, die Dichte und der Verzerrungsgeschwindigkeitstensor objektiv sind (siehe Euklidische Transformation), sind die Navier-Stokes-Gleichungen invariant gegenüber einem Wechsel des Bezugssystems.

Im wichtigen Sonderfall der Inkompressibilität, die bei Strömungsgeschwindigkeiten weit unterhalb der Wellenausbreitungsgeschwindigkeit im Fluid in guter Näherung angenommen werden kann, vereinfacht sich diese Gleichung zu

{\boldsymbol {\sigma }}=-p\mathbf {I} +2\mu \mathbf {d}

und der Druck p ergibt sich nicht mehr aus einer konstitutiven Beziehung, sondern allein aus den Randbedingungen und der Impulsbilanz. Bei großen Reynoldszahlen oder abseits von Grenzschichten können die viskosen Anteile vernachlässigt werden:

{\boldsymbol {\sigma }}=-p(\rho )\mathbf {I} \,.

Ein Fluid mit diesem Spannungstensor gehorcht den Euler-Gleichungen der Strömungsmechanik. Wenn hier die Dichte eine eineindeutige Funktion des Drucks ist, dann ist das Fluid Cauchy-elastisch und konservativ, Kompressionsarbeit in ihm jedenfalls reversibel.

Neben diesen klassischen Materialmodellen betrachtet die Strömungsmechanik auch jedes andere fließende Material, unter anderem Plasma, nicht-newtonsche Fluide oder duktile Materialien bei großen Verformungen, wo die elastische Deformation gegenüber der plastischen vernachlässigt werden kann.

Literatur

H. Oertel (Hrsg.): Prandtl-Führer durch die Strömungslehre. Grundlagen und Phänomene. 13. Auflage. Springer Vieweg, 2012, ISBN 978-3-8348-1918-5.
F. Durst: Grundlagen der Strömungsmechanik. Springer, 2006, ISBN 3-540-31323-0.
G. Bollrich: Technische Hydromechanik 1. Grundlagen. Verlag Bauwesen, 2007, ISBN 3-345-00912-9.
A. Dillmann, K. Wieghardt: Theoretische Strömungslehre. Universitätsverlag Göttingen, 2005, ISBN 3-938616-33-4.
G. K. Batchelor: An Introduction to Fluid Dynamics. Cambridge University Press, 1967, ISBN 0-521-04118-X.
P. K. Kundu: Fluid Mechanics. Academic Press, 2015, ISBN 978-0-12-405935-1.
Wolfgang Schröder: Fluidmechanik. Wissenschaftsverlag Mainz in Aachen, Aachen 2004, ISBN 3-86130-371-X.
Jann Strybny: Ohne Panik Strömungsmechanik. 2. Auflage. Vieweg, 2005, ISBN 3-528-13194-2.

Weblinks

Commons: Strömungsmechanik – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Strömung – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wikibooks: Mechanik flüssiger und gasförmiger Körper – Lern- und Lehrmaterialien

Einzelnachweise

F. Durst: Grundlagen der Strömungsmechanik. Springer, 2006, ISBN 3-540-31323-0, S. 10–16.
H. Oertel (Hrsg.): Prandtl-Führer durch die Strömungslehre. Grundlagen und Phänomene. 13. Auflage. Springer Vieweg, 2012, ISBN 978-3-8348-1918-5, S. 58.
Nam-Trung Nguyen: Mikrofluidik. Entwurf, Herstellung und Charakterisierung. Vieweg+Teubner Verlag, 2004, ISBN 978-3-519-00466-0.
H. Oertel: Bioströmungsmechanik. Grundlagen, Methoden und Phänomene. 2. Auflage. Vieweg+Teubner, 2012, ISBN 978-3-8348-1765-5.
Peter A. Davidson: An introduction to magnetohydrodynamics. Cambridge Univ. Press, Cambridge 2006, ISBN 978-0-521-79487-9.
Peter Haupt: Continuum Mechanics and Theory of Materials. Springer, 2002, ISBN 3-540-43111-X.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] F. Durst: Grundlagen der Strömungsmechanik. Springer, 2006, ISBN 3-540-31323-0, S. 10–16.

[2] H. Oertel (Hrsg.): Prandtl-Führer durch die Strömungslehre. Grundlagen und Phänomene. 13. Auflage. Springer Vieweg, 2012, ISBN 978-3-8348-1918-5, S. 58.

[3] Nam-Trung Nguyen: Mikrofluidik. Entwurf, Herstellung und Charakterisierung. Vieweg+Teubner Verlag, 2004, ISBN 978-3-519-00466-0.

[4] H. Oertel: Bioströmungsmechanik. Grundlagen, Methoden und Phänomene. 2. Auflage. Vieweg+Teubner, 2012, ISBN 978-3-8348-1765-5.

[5] Peter A. Davidson: An introduction to magnetohydrodynamics. Cambridge Univ. Press, Cambridge 2006, ISBN 978-0-521-79487-9.

[6] Peter Haupt: Continuum Mechanics and Theory of Materials. Springer, 2002, ISBN 3-540-43111-X.