Schwimmstabilität
Unter der Schwimmstabilität versteht man das Verhalten eines schwimmenden Körpers bezüglich seiner Lage zu einer Flüssigkeitsoberfläche.
Ein Körper auf einer Flüssigkeit taucht in diese hinein und verdrängt dabei die den Körper umgebende Flüssigkeit. Dabei entsteht eine Auftriebskraft. Die über den Körper verteilte Auftriebskraft wirkt so, als ob sie in ihrer Gesamtheit im räumlichen Mittelpunkt des eintauchenden Teils des Körpers senkrecht nach oben zieht. Dagegen wirkt die über das Volumen eines Körpers verteilte Gewichtskraft stets so, als ob sie in ihrer Gesamtheit im Schwerpunkt des Körpers konzentriert senkrecht nach unten zieht.
Regeln
Schwimmen, Schweben oder Sinken
Ein Körper in einer Flüssigkeit sinkt solange nach unten, wie die Masse der verdrängten Flüssigkeit kleiner ist als die Masse des Körpers. Dies ist das Archimedische Prinzip. Wenn die Gewichtskraft des eintauchenden Körpers und die Auftriebskraft gleich groß sind und ein Teil des Körpers noch aus dem Wasserspiegel ragt, stellt sich ein Schwimmzustand als Gleichgewicht ein. Der aus dem Wasser ragende Teil bewirkt, dass sich bei jedem weiteren minimalen Eintauchen die Auftriebskraft vergrößert und damit den Körper weiter schwimmend hält.
Wenn die Masse des vollständig eingetauchten Körpers und das Gewicht der verdrängten Flüssigkeit exakt gleich groß sind, stellt sich ein Schwebezustand ein. Bereits die geringste Volumenänderung durch Temperatur- oder Druckveränderungen führt zum Auftauchen oder Sinken. Dies wird beim Cartesischen Taucher ausgenutzt. Ist die Masse des vollständig eingetauchten Körpers größer als das Gewicht der verdrängten Flüssigkeit, sinkt der Körper.
Geometrische Lage zum Flüssigkeitsspiegel
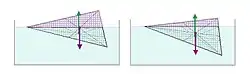
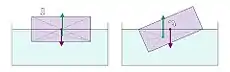
- Die Eintauchtiefe im Gleichgewicht wird von der Masse des Tauchkörpers und von der Dichte der Flüssigkeit bestimmt.
- In einer Flüssigkeit tendiert der Schwerpunkt eines Körpers dazu, die tiefste mögliche Lage einzunehmen.
- Die geometrische Schwimmlage wird von der Form des eintauchenden Körpers, seinem Gewicht und dessen Verteilung sowie auch der Dichte der Trägerflüssigkeit bestimmt.
Dynamisches Verhalten
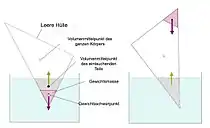
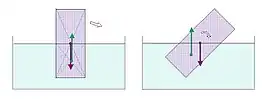
Ein hochkant gestellter quaderförmiger Schwimmkörper hat für die Gewichtskraft und die Auftriebskraft deutlich weiter auseinanderliegende Angriffspunkte. Die Schwimmlage ist daher sehr labil.
- Wird ein schwimmender Körper aus seiner stabilen Schwimmlage gebracht, verschiebt sich stets der Mittelpunkt des eingetauchten Volumens, während der Körperschwerpunkt bei unveränderlichen Körpern gleich bleibt.
- Wenn sich die Angriffspunkte für die Gewichtskraft und die Auftriebskraft nicht lotrecht auf einer vertikalen Achse befinden, entsteht zwischen den beiden Kräften ein Drehmoment, das den Körper solange dreht, bis sich die Kraftangriffspunkte in einer gemeinsamen senkrechten Linie befinden.
- Je weiter der Angriffspunkt für die Gewichtskraft oberhalb des Angriffspunktes für die Auftriebskraft liegt, umso labiler ist ein „Gleichgewichtszustand“, der sich allein auf die senkrechte Lage von Schwerpunkt und Tauchvolumen-Mittelpunkt untereinander bezieht. Bereits bei geringfügigem Kippen verschieben sich diese Punkte gegeneinander und drehen den Körper, bis er sich in stabiler Lage auf dem Flüssigkeitsspiegel befindet.
Quantitative Beschreibung
Eine quantitative Beschreibung erfolgt anhand der gedanklichen Konstruktion eines „Metazentrums“ im Schnittpunkt der verschobenen Kraftwirkungslinien und der davon abgeleiteten „metazentrischen Höhe“.