Direkte Numerische Simulation

Unter Direkter Numerischer Simulation, kurz DNS, versteht man eine Berechnungsmethode der Strömungsmechanik zur rechnerischen Lösung der vollständigen instationären Navier-Stokes-Gleichungen. Sie unterscheidet sich von anderen Berechnungsmethoden der Strömungsmechanik dadurch, dass kleinskalige turbulente Schwankungen numerisch in Raum und Zeit aufgelöst und nicht durch Turbulenzmodelle dargestellt werden.

Aufgrund der zeitlich variierenden, räumlich kleinen Schwankungen in einer turbulenten Strömung ist neben der hohen räumlichen Auflösung eine instationäre Betrachtungsweise für die detaillierte Beschreibung der physikalischen Vorgänge erforderlich. Die DNS ist damit die genaueste Methode, Strömungen zu berechnen; sie stellt allerdings auch die höchsten Anforderungen an das numerische Verfahren sowie an die zur Verfügung stehende Rechenleistung. Deshalb findet die DNS hauptsächlich in der Grundlagenforschung Verwendung. Ein großer Anwendungsbereich ist der laminar-turbulente Umschlag, unter dem man den Übergang von einer glatten stationären Strömung in den quasichaotischen turbulenten Zustand versteht. Des Weiteren wird die DNS in den Bereichen Ablöseblasen, vollturbulente Strömungen und Aeroakustik eingesetzt und dient auch der Weiterentwicklung von Turbulenzmodellen.[1]

Zugrunde liegende Gleichungen

Strömungsfelder verhalten sich gemäß der Navier-Stokes-Gleichungen. Für niedrige Geschwindigkeiten bei einer Mach-Zahl kleiner als 0,3 reicht es in der Regel die Navier-Stokes-Gleichungen für inkompressible Fluide anzuwenden. Sie bestehen im Wesentlichen aus drei Transportgleichungen, den Impulsgleichungen in den drei Raumrichtungen. Aus der Massenerhaltung ergibt sich für inkompressible Strömungen die Divergenzfreiheit der Geschwindigkeit. Mit zunehmender Geschwindigkeit spielen Kompressibilitätseffekte zunehmend eine Rolle, so dass die Navier-Stokes-Gleichungen für kompressible Fluide anzuwenden sind. Diese sind auch erforderlich, wenn zum Beispiel aeroakustische Phänomene untersucht werden sollen, da sich nur bei Berücksichtigung der Kompressibilität eine endliche Schallgeschwindigkeit ergibt. Da die Navier-Stokes-Gleichungen für kompressible Strömungen durchgehend Transportgleichungen sind, gibt es im Gegensatz zu den Gleichungen für inkompressible Fluide keine elliptischen Terme. Je nach Anwendungsfall können zusätzliche Gleichungen mit einbezogen werden. So spielen etwa im Hyperschall bei hoher Mach-Zahl chemische Reaktionen wie Dissoziation von Molekülen oder Ionisation von Atomen eine Rolle.

Physikalische Prozesse

Da in einer DNS das Strömungsfeld ohne Turbulenzmodell berechnet werden soll, lassen sich die vom Verfahren zu erfassenden strömungsmechanischen Vorgänge am anschaulichsten anhand des laminar-turbulenten Umschlags beschreiben. Unter dem Begriff Umschlag, auch Transition genannt, versteht man hierbei den Übergang von einer ursprünglich laminaren stationären Strömung zu einem turbulenten Zustand, der von kleinskaligen nahezu chaotischen Schwankungen bestimmt ist. Die Ursache hierfür ist eine Instabilität der Strömung gegenüber kleinen Störungen, die abhängig vom jeweiligen Strömungszustand ab einer gewissen Reynolds-Zahl existiert. Bereits mit Hilfe der Linearen Stabilitätstheorie lassen sich die Frequenzen der angefachten Störungen und deren Anfachungsraten sehr gut für ein gegebenes stationäres Strömungsfeld vorhersagen. Für eine inkompressible Plattengrenzschicht ohne Druckgradient ergeben sich z. B. angefachte Störungen ab einer Reynolds-Zahl von Re⋅x ≈ 91.000, wobei x die Koordinate in Strömungsrichtung mit ihrem Ursprung an der Plattenvorderkante darstellt. Anstelle der Stromabkoordinate wird häufig die lokale Verdrängungsdicke δ₁ der Grenzschicht verwendet. Damit ergibt sich eine kritische Reynolds-Zahl von Reδ₁=520, ab der das erste Mal angefachte Störungen existieren. Diese angefachten Störungen, Tollmien-Schlichting-Wellen genannt, wachsen in Stromabrichtung exponentiell an. Erreichen die Instabilitätswellen eine merkliche Amplitude, sind sie nicht mehr unabhängig voneinander zu betrachten, sondern wechselwirken miteinander. In den Navier-Stokes-Gleichungen ergibt sich dies aus den nichtlinearen Termen. Unterteilt man eine Größe U in ihren stationären Anteil u₀ sowie den instationären Anteil u, so ergibt sich aus einem nichtlinearen Term

U\cdot U=(u_{0}+u)\cdot (u_{0}+u)=u_{0}^{2}+2\cdot u_{0}u+u^{2}

Nimmt man für den instationären Anteil eine Welle der Form

u=u'\cdot e^{i(\alpha x)}

mit der Wellenzahl α, so ergibt sich aus dem Produkt von u mit sich selbst

U\cdot U=u_{0}^{2}+2u_{0}u'\cdot e^{i(\alpha x)}+u'^{2}\cdot e^{i(2\alpha x)}

das heißt, es werden Wellen mit der doppelten Wellenzahl generiert. Die nichtlineare Generierung bewirkt ein Anwachsen auch von eigentlich linear gedämpften Störungen. Zunehmend kurzwelligere Störungen erreichen nichtlineare Amplituden und ziehen Energie aus den gröberen Skalen ab. Da die zweite Raumableitung einer Welle proportional zum Quadrat der Wellenzahl ist, wirkt für kurzwelligere Störungen jedoch zunehmend die Viskosität der Generierung entgegen.

Je nach eingebrachten Störungen ergeben sich unterschiedliche Wirbelstrukturen im nichtlinearen Bereich. So wird bei der Grenzschicht zwischen K-Typ (nach Philip Klebanoff[2]), H-Typ (nach Thorwald Herbert[3]) und Oblique (englisch für schief) unterschieden. In den Spätstadien der Transition brechen die großen Wirbelstrukturen auf und es ergibt sich ein chaotisches Bild aus kleinen Wirbeln. Zweidimensionale DNS sind nur in Ausnahmefällen sinnvoll. Generell gilt, dass eine 2D-Turbulenz nicht existiert. Deshalb ist es für eine DNS im Allgemeinen notwendig, die vollen dreidimensionalen Navier-Stokes-Gleichungen zu simulieren, was einen entsprechend hohen Rechenaufwand bedeutet.

Künstliches Schlierenbild des Umschlags laminar-turbulent in einer Plattengrenzschicht, berechnet mittels DNS.

Vergleich mit anderen Methoden

Von einer DNS spricht man, wenn alle relevanten Skalen räumlich und zeitlich aufgelöst werden. Dies bedeutet, dass Wellenzahlen soweit sauber abgebildet werden müssen, bis nur mehr der Einfluss der Viskosität der nichtlinearen Generierung entgegenwirkt. Andere Methoden der numerischen Strömungsmechanik betrachten die instationären Vorgänge der Turbulenz entweder eingeschränkt oder überhaupt nicht. Bei der Large-Eddy-Simulation (LES, im deutschen auch Grobstruktursimulation) beschränkt man sich auf die groben turbulenten Skalen, indem man räumlich gefilterte Strömungsgrößen betrachtet. Der Einfluss der nicht mehr aufgelösten Skalen wird durch sogenannte Subgridscale-Modelle abgebildet. Da diese Modelle im Wesentlichen künstliche Viskosität einbringen, kann eine unteraufgelöste DNS auch als LES angesehen werden.

Im Gegenzug dazu werden bei RANS-Rechnungen (englisch für Reynolds-gemittelte Navier-Stokes-Gleichungen) keinerlei turbulente Schwankungen aufgelöst, sondern vollständig durch Turbulenzmodelle modelliert. Mit den zeitlich gemittelten Navier-Stokes-Gleichungen werden auch andere Gleichungen als bei DNS und LES gelöst, weshalb ein RANS-Ergebnis auch bei beliebig feiner Auflösung nicht gegen die exakte Lösung der direkten numerischen Simulation konvergiert.

Diskretisierungsverfahren in der DNS

Skizze eines Integrationsgebietes für die DNS einer Plattengrenzschicht.

Aufgabe eines numerischen Verfahrens zur Direkten Numerischen Simulation ist es somit, instationäre Wellenprozesse ausreichend fein in Raum und Zeit aufzulösen. Außerdem ist auf passende Randbedingungen zu achten, um ein nicht unnötig großes Rechengebiet zu benötigen sowie um Reflexionen an den Rändern zu vermeiden. Typischerweise sind zusätzlich Störungen einzuleiten. Grundsätzlich sind zwar Störungen bereits immanent im Verfahren enthalten (z. B. Diskretisierungsfehler, Näherungen in den Anfangs- und Randbedingungen oder Rundungsfehler), jedoch ist das Ergebnis dann abhängig vom verwendeten Rechengitter und für Rundungsfehler sogar vom verwendeten Rechner. Außerdem möchte man bei einer DNS den Einfluss von unterschiedlichen Störungen untersuchen.

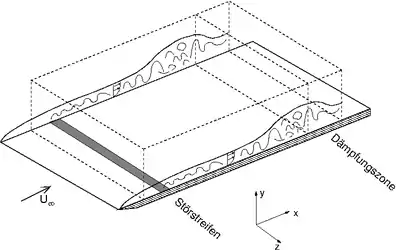
Aufgrund des hohen Rechenaufwandes beschränkt man sich bei der DNS üblicherweise auf periodische Randbedingungen in der dritten Raumrichtung. Für die Grenzschicht an einer ebenen Platte bedeutet dies, dass von einer unendlichen Ausdehnung in Quer- beziehungsweise Spannweitenrichtung ausgegangen wird. Bei rotationssymmetrischen Körpern entspricht die Spannweitenrichtung dann der Umfangsrichtung. Das nebenstehende Bild zeigt beispielhaft ein Integrationsgebiet für die Plattengrenzschicht.

Da der Erfolg einer DNS wesentlich von der Fähigkeit abhängt, Wellen ausreichend exakt zu transportieren, sind entsprechende Anforderungen an die Numerik zu stellen. Bei der Raumdiskretisierung sind gute Dispersions- und Dissipationseigenschaften zu erreichen,[4] weshalb fast ausschließlich Verfahren hoher Ordnung verwendet werden. Für die spannweitige Richtung ist aufgrund der Periodizität ein Spektralansatz geeignet, da dieser ideal für den Wellentransport ist. In nicht-periodischen Raumrichtungen ist ein spektraler Ansatz zwar möglich, jedoch sind Diskretisierungsmethoden, die nicht auf periodischen Randbedingungen basieren, praktikabler. Beispiele dafür sind Finite Differenzen oder Finite Volumen. Häufig werden in DNS-Codes Finite Differenzen verwendet, da sie auf strukturierten Gittern die schnellste Methode zur Berechnung von Raumableitungen hoher Ordnung sind.

Aufgrund der stetigen Generierung von höherharmonischen Wellen ist es für die Stabilität einer Rechnung erforderlich, kurzwellige Störungen zu entfernen. Das Problem der kurzwelligen Anteile ist, dass auf einem gegebenen Gitter nur Wellen bis zu einer bestimmten Wellenzahl aufgelöst werden können. Werden jedoch Wellen mit Wellenzahlen oberhalb dieser Grenze generiert, so werden diese zu gewissen Anteilen auf niedrigere Wellenzahlen abgebildet (sogenanntes Aliasing), was im Allgemeinen zum Absturz des Verfahrens führt. Auch für die Wellentransporteigenschaften jeder räumlichen Diskretisierung existiert eine Aliasing-Grenze. Für Wellenzahlen oberhalb dieser Aliasing-Grenze ergibt sich eine negative Gruppengeschwindigkeit, das heißt diese instationären Anteile laufen entgegen der physikalisch richtigen Transportrichtung. Ab welcher Wellenzahl dies auftritt, hängt von der Art und der Ordnung des Verfahrens ab. Mit zunehmender Ordnung wandert die Aliasing-Grenze zu höheren Wellenzahlen. Prinzipiell ist ein Entfernen der kurzwelligen Anteile auch durch eine entsprechend hohe räumliche Auflösung möglich. In diesem Fall sorgt die Viskosität für eine Dämpfung dieser Anteile. Dies ist jedoch nicht praktikabel, da dies eine allzu große räumliche Auflösung erfordert. Gängige Methoden zum Dealiasing sind räumliche Filterung mit einem Tiefpassfilter,[4] Upwinding oder eine abwechselnde Gewichtung der Diskretisierung.[5] Bei einer spektralen Diskretisierung sind die Anteile in Abhängigkeit von der Wellenzahl gegeben. Dealiasing erfolgt dann einfach durch Nullsetzung hoher Wellenzahlen (üblicherweise ab 2/3 der maximalen Wellenzahl.[6])

Aus den Navier-Stokes-Gleichungen ergibt sich mittels der Raumdiskretisierung die Zeitableitung der einzelnen Größen. Prinzipiell kann die Zeitintegration mit expliziten oder impliziten Verfahren durchgeführt werden. Bei einer expliziten Zeitintegration ist das Zeitschrittlimit für eine stabile Simulation einzuhalten. Je nachdem, ob konvektive oder viskose Terme überwiegen, skaliert der Zeitschritt proportional oder quadratisch mit der räumlichen Auflösung. Häufig wird das Runge-Kutta-Verfahren 4. Ordnung für die Zeitintegration angewendet, da es hervorragende Eigenschaften bezüglich Genauigkeit und Stabilität aufweist. Implizite Verfahren haben zwar den Vorteil, (zumindest prinzipiell) kein Zeitschrittlimit zu besitzen, jedoch erfordern sie einen deutlich höheren Rechenaufwand pro Zeitschritt. Wählt man den Zeitschritt so grob, so dass sich ein implizites im Vergleich zu einem expliziten Verfahren lohnt, so dämpft die implizite Integration nahezu alle Instabilitätswellen weg. Aus diesem Grund werden implizite Integrationsverfahren bei DNS-Codes in der Regel nicht angewendet. Eine Ausnahme davon stellen kompressible Rechnungen bei niedriger Mach-Zahl dar, bei denen der Zeitschritt eines expliziten Verfahrens sehr fein sein muss.

Aufgrund des hohen Rechenaufwandes ist es meist unerlässlich, auf mehreren Prozessoren zu rechnen. Da DNS-Codes typischerweise auf strukturierten Gittern arbeiten und sich damit gut vektorisieren lassen, kann auf Vektorrechnern (z. B. Earth Simulator oder NEC-SX8) eine hohe Rechenleistung erreicht werden, die teilweise über 50 % der theoretischen Rechenleistung erreicht. Unstrukturierte Verfahren konnten sich bislang in DNS-Codes nicht durchsetzen, da die größere Flexibilität im Hinblick auf die Geometrie zu Lasten der Rechengeschwindigkeit geht.

Anfangs- und Randbedingungen

Räumliche und zeitliche Simulationen

Wie in der Linearen Stabilitätstheorie unterscheidet man zwischen zeitlichem und dem räumlichen Problem. Bei einer zeitlichen Simulation werden Störungen, die über den Ausströmrand das Integrationsgebiet verlassen, am Einströmrand wieder eingebracht. Dies bedeutet, dass Störungen in der Zeit bis zur Sättigung anwachsen. Hintergrund dieser Vorgehensweise ist die Tatsache, dass aus mathematischer Sicht wegen des parabolischen Charakters der viskosen Terme auch am Ausströmrand Randbedingungen vorzugeben sind. Durch einen periodischen Ansatz in Strömungsrichtung wird das Problem umgangen, die in der Regel unbekannten passenden Randbedingungen vorzugeben. Ein Problem hierbei ist natürlich die Tatsache, dass die Strömung am Ausströmrand nicht den gleichen Zustand wie am Einströmrand aufweist. So wächst etwa eine Grenzschicht in Stromabrichtung an oder in einem Kanal sorgt ein Druckgradient dafür, dass die Strömung nicht zum Erliegen kommt. Deshalb sind die Störgrößen entsprechend zu skalieren, bevor sie am Einströmrand aufgeprägt werden können. Trotz der Probleme und Einschränkungen des zeitlichen Modells wird es bis heute verwendet, da mit einem relativ kleinen Integrationsgebiet eine turbulente Strömung berechnet werden kann.

Bei einer räumlichen Simulation hingegen werden Ein- und Ausströmrand getrennt voneinander betrachtet. Damit wachsen Störungen räumlich an (mit Ausnahme vom Auftreten einer absoluten Instabilität) was deutlich besser die Realität wiedergibt. In einer Grenzschicht etwa werden Tollmien-Schlichting-Wellen stromab transportiert, während sie anwachsen, was einer Zunahme der Amplitude in Stromab-Richtung entspricht. Nach ausreichender Simulationszeit erreichen die Störungen bei zeitlich periodischer Störungsanregung einen in der Zeit periodischen Zustand. Besonders wichtig ist bei einer räumlichen Simulation die Modellierung eines geeigneten Ausströmrandes, da ein Auftreffen von nichtlinearen Störungen auf den Ausströmrand Reflexionen verursachen würde, was wiederum zu unphysikalischen Ergebnissen führt. Anfangs wurde das Integrationsgebiet mit der Zeit in Stromab-Richtung verlängert, so dass Störungen nie den nach hinten laufenden Ausströmrand erreichen konnten. Diese Methode wird jedoch mit zunehmender Simulationsdauer immer aufwändiger. Der Durchbruch der räumlichen Simulation gelang erst mit der Entwicklung von geeigneten Dämpfungszonen vor dem Ausströmrand.[7] Heutzutage wird zum Großteil das räumliche Modell verwendet.

Anfangsbedingungen

Als Anfangsbedingung wird typischerweise eine Lösung der Grenzschichtgleichungen verwendet, da diese eine gute Approximation einer laminaren reibungsbehafteten Strömung darstellen. Bei einer Plattengrenzschicht können selbstähnliche Profile (Blasius oder Falkner-Skan) auf das Rechengitter interpoliert werden. Handelt es sich um komplexere Geometrien, so sind die Grenzschichtgleichungen in Stromabrichtung zu integrieren. Ist dies nicht möglich, z. B. wegen Rückströmung, so kann das Strömungsfeld auch mit einfachen Annahmen initialisiert werden, da bei sauberen Randbedingungen Anfangsstörungen aus dem Integrationsgebiet heraus laufen sollten.

Randbedingungen

Für eine Wand lassen sich die Randbedingungen vergleichsweise einfach formulieren. Aufgrund der Reibung sind die drei Geschwindigkeitskomponenten an der Wand Null (Haftbedingung). Im kompressiblen Fall ist eine weitere Randbedingung für die Temperatur zu geben, die wahlweise isotherm oder adiabat sein kann. Isotherm bedeutet, dass die Temperatur fest vorgeschrieben ist, adiabat, dass der Wärmestrom und damit der wandnormale Temperaturgradient null ist. Weiterhin können Aktuatoren an der Wand platziert werden, wie z. B. ein Störstreifen zur Störungsanregung, um das Verhalten bestimmter Störmoden zu untersuchen.

Am Einströmrand sind bei inkompressiblen Rechnungen und im Überschall sämtliche Strömungsgrößen vorzuschreiben. Bei kompressiblen Rechnungen im Unterschall ist z. B. durch eine charakteristische Randbedingung dafür zu sorgen, dass stromauflaufende Schallwellen das Integrationsgebiet verlassen können. Der Einströmrand eignet sich auch um definierte Störungen einzubringen. Bei kleinen Störungen kann hierzu z. B. auf Amplituden- und Phasenverläufe aus der Linearen Stabilitätstheorie zurückgegriffen werden.

Problematisch sind grundsätzlich Randbedingungen, die sich nur aufgrund des endlichen Rechengitters ergeben. Während bei RANS-Rechnungen typischerweise nur die stationären Freistrombedingungen vorgeschrieben werden, ist aufgrund der instationären Lösung die Wahl geeigneter Randbedingungen für den Erfolg einer DNS entscheidend. Eine besondere Bedeutung kommt hierbei dem Ausströmrand zu, da Reflexionen aufgrund der nichtlinearen Fluktuationen das Ergebnis signifikant verfälschen können. Hierzu wurden in der Vergangenheit verschiedene Dämpfungszonen entwickelt, in denen z. B. die Lösung auf eine stationäre Grundströmung gezogen wird.[7] Insbesondere für aeroakustische Rechnungen ergeben sich besonders strenge Anforderungen an den Ausströmrand, da der betrachtete Schall um Größenordnungen kleiner als die strömungsmechanischen Schwankungen ist. Eine Möglichkeit ist hierbei die Kombination von Gitterstreckung und räumlichem Tiefpassfilter, wodurch instationäre Anteile in der Dämpfungszone sukzessive aus der Lösung zu entfernen werden bevor diese am eigentlichen Rand Reflexionen verursachen und das empfindliche akustische Feld kontaminieren können.[8]

Freistromränder sind grundsätzlich weniger kritisch als Ausströmränder, da die auftretenden Amplituden deutlich geringer sind als beim Ausströmrand. Allerdings können ungeeignete Randbedingungen zu falschen Anfachungsraten der Störwellen führen oder die richtige Lösung erfordert ein zu großes Integrationsgebiet. Aufgrund der kleinen Schwankungen basieren die Freistromränder typischerweise auf linearisierte Formulierungen, wie z. B. Abkling- oder charakteristische Randbedingungen. Wird Periodizität in Querrichtung angenommen, stellt sich die Frage nach passenden Randbedingungen an dieser Stelle nicht.

Skalierung des Problems mit der Reynolds-Zahl

Die aufzulösenden Skalen werden durch die Physik bestimmt. Das Rechengitter definiert, welche Skalen bei einem bestimmten numerischen Verfahren aufgelöst werden können. Die sich daraus ergebende erforderliche Schrittweite muss somit in der Größenordnung von (proportional zu und nicht gleich) den kleinsten Skalen sein, die durch die Kolmogorow-Längenskala

\eta =(\nu ^{3}/\varepsilon )^{1/4}

bestimmt werden, wobei $\nu$ die kinematische Viskosität und ε die Dissipationsrate der kinetischen Energie ist. Bei einer räumlichen Schrittweite h ist die Anzahl der Punkte N in einer Raumrichtung

N\sim {\frac {L}{h}}\sim {\frac {L}{\eta }}

.

Die Dissipationsrate ε der kinetischen Energie lässt sich mit dem RMS-Wert der Geschwindigkeitsschwankung u' abschätzen zu

\varepsilon \approx u'^{3}/L

.

Somit ergibt sich für die Anzahl der benötigten Punkte in einer Raumrichtung

N\sim {\frac {L}{\eta }}=\left({\frac {Lu'}{\nu }}\right)^{3/4}=\mathrm {Re} ^{3/4}

mit der Reynolds-Zahl

\mathrm {Re} ={\frac {u'L}{\nu }}

.

Unterliegen alle drei Raumrichtungen der Skalierung mit der Reynolds-Zahl, so wächst die Gesamtanzahl der benötigten Punkte mit Re^9/4. Geht man von periodischen Randbedingungen in spannweitiger Richtung aus, so ist eine Skalierung der Punkte in dieser Richtung mit Re^3/4 nicht zwingend erforderlich, wodurch die Gesamtauflösung nur noch mit Re^3/2 skaliert. Dies kann sich weiter reduzieren, da z. B. die Grenzschichtdicke nicht linear mit der Stromabrichtung anwächst, weshalb die Anzahl der Punkte in wandnormaler Richtung schwächer als mit Re^3/4 skalieren kann. Die zu simulierende Zeit ist proportional der turbulenten Längenskala τ, die durch

\tau ={\frac {L}{u'}}

gegeben ist. Unter der Annahme, dass das Zeitschrittlimit durch konvektive Terme dominiert wird (Δt ∼ h ∼ η/u'), ergibt sich die Anzahl der Zeitschritte zu

N_{t}\sim {\frac {\tau }{\Delta {}t}}\sim {\frac {L}{\eta }}=\mathrm {Re} ^{3/4}

das heißt, die Anzahl der zu rechnenden Zeitschritte skaliert mit der Potenz ¾ der Reynolds-Zahl. Somit ist der gesamte Rechenaufwand proportional zu Re³ für ein voll-dreidimensionales Integrationsgebiet ohne spannweitige Periodizität.

Bei einem Skalierungsfaktor des Gesamtproblems von Re^9/4 beziehungsweise Re³ erscheint eine Anwendung der DNS auf praxisrelevante Probleme auf den ersten Blick als ausgeschlossen. Eine Auswertung so großer Datenmengen (man beachte, dass es sich hierbei um instationäre Probleme handelt) erscheint auch nicht praktikabel. Bei der DNS geht es jedoch nicht darum, etwa ein komplettes Flugzeug zu simulieren, vielmehr ist man an den physikalischen Grundlagen interessiert, durch deren Verständnis auch ein Gesamtsystem mit hohen Reynolds-Zahlen, wie zum Beispiel das Profil eines Tragflügels, verbessert werden kann. Entwickelt man etwa Methoden zur Laminarhaltung, so ist es ausreichend, den relevanten Bereich der Grenzschicht zu simulieren, um damit den Widerstand des gesamten Flugzeugs zu verringern.

Auswertung der Ergebnisse

Momentanbild von Wirbelstrukturen in einer Scherschicht. Durch das Einbringen stationärer spannweitiger Störungen werden Längswirbel erzeugt, die zum Zusammenbrechen der Kelvin-Helmholtz-Wirbel führen.[9]

Da man aus der DNS instationäre Daten von großen Gebieten erhält (um die 100 Millionen Gitterpunkte für die Raumauflösung sind durchaus üblich), fallen riesige Datenmengen von etlichen Gigabyte an. Daraus sind natürlich nicht direkt Aussagen über die physikalischen Vorgänge ableitbar, es bedarf einer Auswertung der Daten (postprocessing). Da beim räumlichen Modell der zeitliche Verlauf nach genügend gerechneten Zeitschritten periodisch oder zumindest quasi-periodisch ist, bietet es sich an, die Daten mittels Fourieranalyse zu untersuchen. Dabei wird bei periodischen Randbedingungen in Spannweitenrichtung häufig eine doppelspektrale Analyse durchgeführt. Die resultierenden Moden werden mit (h,k) bezeichnet, wobei h ein Vielfaches der Grundfrequenz und k ein Vielfaches der spannweitigen Grundwellenzahl

$\gamma ={\frac {2\pi }{\lambda _{z}}}$

ist, welche sich aus der spannweitigen Ausdehnung λ_z des Integrationsgebiets ergibt. So bezeichnen die Moden (0,1), (0,2) usw. stationäre Störungen, die über der dritten Raumrichtung modelliert sind. Entsprechend wird eine zweidimensionale Störung mit der Fundamentalfrequenz mit (1,0) und ihre Höherharmonischen mit (2,0), (3,0) usw. bezeichnet. Das Wachstum der Amplituden in Strömungsrichtung sowie der Amplituden- bzw. Phasenverlauf normal dazu kann auch mit Ergebnissen der linearen Stabilitätstheorie verglichen werden.

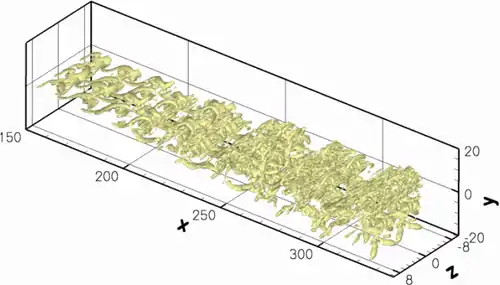
Im turbulenten Bereich sind Amplitudenverläufe in der Regel weniger aussagekräftig, da eine Vielzahl der Moden die Sättigung erreicht hat. Deshalb werden Wirbel z. B. mit Hilfe des lambda2-Kriteriums[10] visualisiert, um einen besseren Einblick in die strömungsmechanischen Mechanismen zu erhalten. Das Bild zeigt beispielhaft dreidimensionale Wirbelstrukturen in einer Scherschicht mittels Isoflächen des lambda2-Kriteriums. Durch das Einbringen stationärer spannweitiger Störungen werden Längswirbel erzeugt, die zum Zusammenbrechen der Kelvin-Helmholtz-Wirbel führen. Um bei aeroakustischen Rechnungen die Schallabstrahlung darzustellen, kann man den Druck selbst, aber auch die Dilatation, die Divergenz des Geschwindigkeitsfeldes, darstellen. Einen schönen Eindruck vermitteln Dichtegradienten, da man damit Schlierenbilder erzeugen kann. Ein Auswerteprogramm ist z. B. EAS3, das an verschiedenen Universitäten zur Auswertung von DNS-Daten eingesetzt wird.

Geschichte der DNS

Den Beginn der numerischen Strömungsmechanik stellt die Berechnung eines Kreiszylinders mit Re=10 aus dem Jahre 1933 dar.[11] Thom erzielte die Lösung durch Handrechnung mittels eines Differenzenverfahrens, welche bereits erstaunlich genau war. Von einer ersten DNS im eigentlichen Sinn kann man bei der Simulation von Orszag & Patterson aus dem Jahre 1972 sprechen, die isentrope Turbulenz bei Re=35 auf einem 32³ Gitter mit spektralen Methoden berechneten.[12] Die erste räumliche DNS stammt von Fasel aus dem Jahre 1976. In dieser wurde das Wachstum kleiner Störungen in einer Grenzschicht untersucht und mit der Linearen Stabilitätstheorie verglichen.[13] Die turbulente Strömung in einem ebenen Kanal mit Re=3300 und periodischen Randbedingungen in Strömungsrichtung wurde von Kim et al. im Jahr 1987 auf einem Gitter mit bereits 4 Millionen Punkten berechnet.[14] Im Jahr 1988 veröffentlichte Spalart DNS-Ergebnisse einer turbulenten Grenzschicht mit Reθ = 1410 (θ steht hierbei für die Impulsverlustdicke der Grenzschicht), denen ebenfalls das zeitliche Modell zugrunde liegt.[15] Ein Durchbruch bei der Anwendung des räumlichen Modells gelang Anfang der 1990er Jahre mit der Entwicklung passender Dämpfungszonen vor dem Ausströmrand, z. B. durch Kloker et al.[7] Mithilfe entsprechender Randbedingungen konnten Colonius et al. 1997 eine der ersten akustischen DNS durchführen, wobei der abgestrahlte Schall der simulierten freien Scherschicht direkt mittels der Navier-Stokes-Gleichungen und nicht nach einer akustischen Analogie berechnet wurde.[8] Die bis heute größte DNS, bezogen auf die räumliche Auflösung, ist eine Rechnung von Kaneda und Ishihara aus dem Jahr 2002, die auf dem Earth Simulator in Japan durchgeführt wurde. Sie verwendeten 4096³ ≈ 68,7 Milliarden Gitterpunkte zur Simulation von isentroper Turbulenz in einem periodischen Integrationsgebiet.[16] Der große Fortschritt, der im Bereich der DNS erzielt wurde, basiert natürlich zum einen auf den stetig steigenden Rechnerkapazitäten, aber ebenso auf den entwickelten numerischen Verfahren, die eine effektive Nutzung dieser Ressourcen erst ermöglichen.

Anwendungsgebiete

Grenzschichtablösung an einem Profil.

Ein Beispiel für die Anwendung ist die Ablösung einer Grenzschicht aufgrund eines der Strömung entgegenwirkenden Druckgradienten. Durch das Anregen der Grenzschicht mit bestimmten Störungen wird versucht, Ablöseblasen zu verkleinern, oder ganz zu vermeiden. Anwendungsbeispiele sind etwa Turbinenschaufeln oder die Tragflügel am Flugzeug. Wäre man in der Lage, den Strömungsabriss bei hohem Anstellwinkel zu vermeiden, könnten höhere Auftriebsbeiwerte erzielt werden und man könnte auf Landeklappen verzichten.

Ein weiteres Thema ist die Laminarhaltung, bei der versucht wird, die Grenzschicht über den natürlichen Bereich hinaus laminar zu halten und den Umschlag von laminar zu turbulent herauszuzögern. Dies geschieht z. B. mit Absaugung oder dem Einbringen von Längswirbeln in die Grenzschicht. Da eine laminare Grenzschicht einen geringeren Widerstand als eine turbulente aufweist, könnte dadurch der Kerosinverbrauch von Flugzeugen um bis zu 15 % reduziert werden.[17]

In der Aeroakustik werden die Mechanismen der Schallentstehung, verursacht durch strömungsmechanische Prozesse, untersucht. Ziel ist es dabei, den abgestrahlten Schall durch entsprechende Aktuatoren zu reduzieren. Die Aeroakustik ist ein relativ neues Feld im Bereich der DNS, da es als Mehrskalenproblem relativ schwierig zu lösen ist. Die strömungsmechanischen Fluktuationen, z. B. in einer freien Scherschicht, haben große Amplituden mit einer kleinen räumlichen Ausdehnung. Der abgestrahlte Schall dagegen ist relativ langwellig mit einer äußerst geringen Amplitude. Daraus ergibt sich, dass besondere Anforderungen (Randbedingungen, Genauigkeit) an ein numerisches Verfahren zu stellen sind, um die Ergebnisse nicht z. B. durch Reflexionen zu verfälschen. Ein wichtiger Teilaspekt ist der Strahllärm, da er eine der Hauptlärmquellen eines Flugzeugs – insbesondere während des Starts – ist. Ein Durchbruch auf diesem Gebiet würde die Lebensqualität vieler Anwohner von Flughäfen erhöhen. Aufgrund von Auflagen wie z. B. Nachtflugverbot oder lärmabhängigen Start-/Landegebühren sind aber auch Fluggesellschaften und Flughafenbetreiber an einer Verringerung des Fluglärms interessiert.

Im Bereich des Über- und Hyperschalls ist es erforderlich, nicht nur zeitlich gemittelte Größen, sondern auch instationäre Vorgänge in der Grenzschicht abzubilden, da hohe thermische Belastungen die Struktur zerstören können. Die DNS wird dabei für Grundlagenuntersuchungen des laminar-turbulenten Umschlags oder zur Entwicklung von Kühlkonzepten eingesetzt. Um Effekte im Hyperschall zu berücksichtigen, werden mittlerweile auch komplexere Gleichungen verwendet, die chemische Reaktionen wie Dissoziation oder Ionisation, sowie thermisches Nichtgleichgewicht berücksichtigen.[18]

Die DNS ist auch ein wichtiges Werkzeug für die Modellbildung. Dabei werden die hochaufgelösten instationären Strömungsdaten für die Weiterentwicklung von Turbulenzmodellen verwendet, um so weniger rechenintensive Verfahren wie Large-Eddy-Simulation oder RANS-Rechnungen zu verbessern. Außerdem können damit die Ergebnisse neuer Methoden der Strömungsmechanik validiert werden.

Siehe auch

Literatur

Parviz Moin, Krishnan Mahesh: Direct Numerical Simulation. A Tool in Turbulence Research. In: Annual Review of Fluid Mechanics. Vol. 30, 1998, S. 539–578, doi:10.1146/annurev.fluid.30.1.539.
Siegfried Wagner, Markus Kloker, Ulrich Rist: Recent Results in Laminar-Turbulent Transition. Springer Verlag, Berlin u. a. 2003, ISBN 3-540-40490-2 (Schriftenreihe: Notes on numerical fluid mechanics and multidisciplinary design 86).
Peter J. Schmid, Dan S. Henningson: Stability and Transition in Shear Flows. Springer Verlag, Berlin u. a. 2001, ISBN 0-387-98985-4 (Applied Mathematical Sciences 142).
Hermann Schlichting, Klaus Gersten: Grenzschicht-Theorie. 9. völlig neubearbeitete und erweiterte Auflage. Springer Verlag, Berlin u. a. 1997, ISBN 3-540-55744-X.
John D. Anderson: Computational Fluid Dynamics. The Basics with Applications. McGraw-Hill, New York u. a. 1995, ISBN 0-07-113210-4 (McGraw-Hill series in aeronautical and aerospace engineering).

Einzelnachweise

Direkte Numerische Simulation & Grobstruktursimulation von turbulenten Strömungen. Abgerufen am 1. Juli 2019.
P. Klebanoff, K. Tidstrom: Evolution of Amplified Waves Leading to Transition in a Boundary Layer with Zero Pressure Gradient. NASA TN D-195, 1959.
T. Herbert: Secondary Instability of Boundary Layers. Annual Review of Fluid Mechanics, Vol. 20, 1988, S. 487–526, doi:10.1146/annurev.fl.20.010188.002415
S. Lele: Compact finite differences with spectral-like resolution. Journal of Computational Physics, Vol. 103, 1992, S. 16–42, ISSN 0021-9991
M. Kloker: A robust high-resolution split-type compact FD scheme for spatial DNS of boundary-layer transition. Applied Scientific Research, Vol. 59, 1998, S. 353–377, doi:10.1023/A:1001122829539
C. Canuto, M. Hussaini, A. Quarteroni: Spectral Methods in Fluid Dynamics. In: Springer series in computational physics, Springer Verlag, New-York 1988, ISBN 0-387-17371-4.
M. Kloker, U. Konzelmann, H. Fasel: Outflow boundary conditions for spatial Navier-Stokes simulations of transition boundary layers. AIAA Journal, Vol. 31, No 4, 1993, S. 355–383, ISSN 0001-1452
T. Colonius, S. Lele, P. Moin: Sound generation in a mixing layer. Journal of Fluid Mechanics, Vol. 330, 1997, S. 375–409, ISSN 0022-1120
A. Babucke, M. Kloker, U. Rist: DNS of a Plane Mixing Layer for the Investigation of Sound Generation Mechanisms. Computers and Fluids, Vol. 37, Issue 4, 2008, S. 360–368, doi:10.1016/j.compfluid.2007.02.002
J. Jeong, F. Hussain: On the identification of a vortex. Journal of Fluid Mechanics, Vol. 285, 1995, S. 69–94, doi:10.1017/S0022112095000462
A. Thom: The flow past a circular cylinder at low speeds. Proceedings of the Royal Society of London. Series A, Vol. 141, 1933, S. 651.
S. Orszag, G. Patterson: Numerical simulation of three-dimensional homogeneous isotropic turbulence. Physical Review Letters, Vol. 28, 1972, S. 76–79, doi:10.1103/PhysRevLett.28.76
H. Fasel: Investigation of the stability of boundary layers by a finite-difference model of the Navier-Stokes equations. Journal of Fluid Mechanics, Vol. 78, No 2, 1976, S. 620–628, doi:10.1017/S0022112076002486
J. Kim, P. Moin, R. Moser: Turbulence statistics in fully-developed channel flow at low Reynolds number. Journal of Fluid Mechanics, Vol. 177, 1987, S. 133–66, doi:10.1017/S0022112087000892
P. Spalart: Direct numerical simulation of a turbulent boundary layer up to Rθ= 1410. Journal of Fluid Mechanics, Vol. 187, 1988, S. 61–98, doi:10.1017/S0022112088000345
Y. Kaneda, T. Ishihara: High-resolution direct numerical simulation of turbulence. Journal of Turbulence, Vol. 7, No. 20, 2006.
Billiger fliegen – mit durchlöcherten Flügeln, Artikel auf Spiegel Online, 2006.
C. Stemmer, N. Mansour: DNS of transition in hypersonic boundary-layer flows including high-temperature gas effects. Center for Turbulence Research, Annual Research Briefs, 2001, pdf (Memento vom 9. Juli 2010 im Internet Archive)

Weblinks

Commons: Direkte Numerische Simulation – Sammlung von Bildern, Videos und Audiodateien

Galerie mit DNS Ergebnissen beim Center of Turbulence Research (Memento vom 18. Mai 2013 im Internet Archive)
Animation der Wirbelstrukturen beim Grenzschichtumschlag (K-Typ)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Direkte Numerische Simulation & Grobstruktursimulation von turbulenten Strömungen. Abgerufen am 1. Juli 2019.

[2] P. Klebanoff, K. Tidstrom: Evolution of Amplified Waves Leading to Transition in a Boundary Layer with Zero Pressure Gradient. NASA TN D-195, 1959.

[3] T. Herbert: Secondary Instability of Boundary Layers. Annual Review of Fluid Mechanics, Vol. 20, 1988, S. 487–526, doi:10.1146/annurev.fl.20.010188.002415

[lele-4] S. Lele: Compact finite differences with spectral-like resolution. Journal of Computational Physics, Vol. 103, 1992, S. 16–42, ISSN 0021-9991

[kloker-5] M. Kloker: A robust high-resolution split-type compact FD scheme for spatial DNS of boundary-layer transition. Applied Scientific Research, Vol. 59, 1998, S. 353–377, doi:10.1023/A:1001122829539

[canuto-6] C. Canuto, M. Hussaini, A. Quarteroni: Spectral Methods in Fluid Dynamics. In: Springer series in computational physics, Springer Verlag, New-York 1988, ISBN 0-387-17371-4.

[kloker-konzelmann-7] M. Kloker, U. Konzelmann, H. Fasel: Outflow boundary conditions for spatial Navier-Stokes simulations of transition boundary layers. AIAA Journal, Vol. 31, No 4, 1993, S. 355–383, ISSN 0001-1452

[colonius-8] T. Colonius, S. Lele, P. Moin: Sound generation in a mixing layer. Journal of Fluid Mechanics, Vol. 330, 1997, S. 375–409, ISSN 0022-1120

[9] A. Babucke, M. Kloker, U. Rist: DNS of a Plane Mixing Layer for the Investigation of Sound Generation Mechanisms. Computers and Fluids, Vol. 37, Issue 4, 2008, S. 360–368, doi:10.1016/j.compfluid.2007.02.002

[jeong-10] J. Jeong, F. Hussain: On the identification of a vortex. Journal of Fluid Mechanics, Vol. 285, 1995, S. 69–94, doi:10.1017/S0022112095000462

[thom-11] A. Thom: The flow past a circular cylinder at low speeds. Proceedings of the Royal Society of London. Series A, Vol. 141, 1933, S. 651.

[orszag-12] S. Orszag, G. Patterson: Numerical simulation of three-dimensional homogeneous isotropic turbulence. Physical Review Letters, Vol. 28, 1972, S. 76–79, doi:10.1103/PhysRevLett.28.76

[fasel-13] H. Fasel: Investigation of the stability of boundary layers by a finite-difference model of the Navier-Stokes equations. Journal of Fluid Mechanics, Vol. 78, No 2, 1976, S. 620–628, doi:10.1017/S0022112076002486

[kim-14] J. Kim, P. Moin, R. Moser: Turbulence statistics in fully-developed channel flow at low Reynolds number. Journal of Fluid Mechanics, Vol. 177, 1987, S. 133–66, doi:10.1017/S0022112087000892

[spalart-15] P. Spalart: Direct numerical simulation of a turbulent boundary layer up to Rθ= 1410. Journal of Fluid Mechanics, Vol. 187, 1988, S. 61–98, doi:10.1017/S0022112088000345

[kaneda-16] Y. Kaneda, T. Ishihara: High-resolution direct numerical simulation of turbulence. Journal of Turbulence, Vol. 7, No. 20, 2006.

[spiegel-17] Billiger fliegen – mit durchlöcherten Flügeln, Artikel auf Spiegel Online, 2006.

[stemmer-18] C. Stemmer, N. Mansour: DNS of transition in hypersonic boundary-layer flows including high-temperature gas effects. Center for Turbulence Research, Annual Research Briefs, 2001, pdf (Memento vom 9. Juli 2010 im Internet Archive)