Wirbel (Strömungslehre)

Als Wirbel oder Vortex bezeichnet man in der Strömungslehre eine drehende Bewegung von Fluidelementen um eine gerade oder geschwungene Drehachse. Der Begriff des Wirbels ist eher intuitiv – siehe Bilder – und mathematisch nicht präzise formulierbar.

Abb. 1: Luftwirbel: Wirbelschleppe (eingefärbt)

Abb. 2: Ein Strudel ist ein Sonderfall eines Wirbels

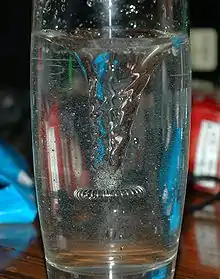
In Fluiden mit niedriger Viskosität (Luft und Wasser) ist die Fließgeschwindigkeit in größeren Wirbeln im Zentrum am größten und nimmt umgekehrt proportional zum Abstand vom Zentrum ab. Die Wirbelstärke ist im Zentrum groß und fast null im äußeren Bereich des Wirbels, weshalb sich Fluidelemente dort kaum um sich selbst drehen. Umgekehrt verhält es sich mit dem Druck, der im Zentrum am niedrigsten ist. Wirbel neigen dazu, ausgedehnte Wirbelröhren auszubilden, die sich mit der Strömung mitbewegen, sich winden, biegen und strecken können.

In der Meteorologie und in der Aerodynamik spielen Wirbel eine wichtige Rolle.

Phänomenologie

Dieser Abschnitt ist der Phänomenologie, d. h. den physikalisch gegebenen Wirbelerscheinungen gewidmet.

Entstehung des Wirbels

Abb. 3: hydrodynamische Simulation einer Rayleigh-Taylor-Instabilität

Abb. 4: Rayleigh-Bénard Konvektionszellen

Wirbel werden durch (gekrümmte) Wände eingeleitet, durch äußere Kräfte angefacht, durch die Drehimpulserhaltung erzwungen oder sind eine Konsequenz des Ausgleichsbestrebens sich selbst überlassener Fluide (Zweiter Hauptsatz der Thermodynamik).

Runde Einfassungen wie das Glas in Abb. 2 oder der Stufensprung bei einer Wasserwalze leiten Strömungen im Kreis. In der Aero- und Hydrodynamik wichtige Wirbel entstehen, wenn sich ein Fahrzeug durch ein Fluid bewegt, speziell wenn sich Flugzeuge oder Autos durch Luft oder Schiffe durch das Wasser bewegen. In Folge von Strömungsabrissen an der A-Säule von Autos oder an einem Zylinder (siehe Animation in Abb. 7) entstehen dauerhafte Wirbelströmungen. Nicht nur bei Orgelpfeifen[1] sind Luftwirbel an der Erzeugung hörbaren Schalls beteiligt.

Eine Kraftwirkung, die Wirbel entstehen lässt, sind Trägheitskräfte in Fluiden, die als Ganzes rotieren, wie zum Beispiel die Erdatmosphäre. Der Corioliseffekt lenkt dabei Strömungen innerhalb des Luftkörpers in eine Kreisbewegung um. Dies ist die Ursache dafür, dass Hoch- und Tiefdruckgebiete in der Atmosphäre Wirbel bilden. Der polare Vortex und der Jetstream sind ebenfalls Wirbel, die durch Trägheitskräfte entstehen.

Wenn Fluide auf ein Zentrum zustreben, dann können Fluidelemente, die Drehimpuls besitzen, nicht einfach geradewegs hinein stürzen: Die Erhaltung des Drehimpulses zwingt sie erst auf eine Kreisbahn um das Zentrum, wodurch im interstellaren Raum protoplanetare Scheiben, das sind Wirbel aus Staub und Gas, um junge Sterne im Zentrum entstehen.

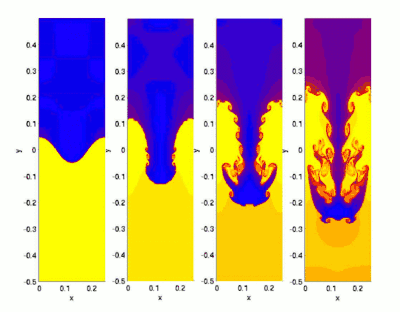
Nur indirekt von äußeren Einflüssen geleitet entstehen Wirbel, wenn Fluidmassen mit unterschiedlichen Eigenschaften aufeinander treffen. Die Fluidmassen können sich unter anderem in ihrer Temperatur, ihrer Geschwindigkeit oder ihrer Dichte unterscheiden. An den Grenzflächen zwischen den Fluidmassen kommt es bei hinreichender Differenz in den Eigenschaften (am Kipp-Punkt) zu Instabilitäten, die zu Wirbeln und im weiteren Verlauf zu turbulenter Strömung führen, in der unterschiedlich große Wirbel die Massen intensiv durchmischen. Ein solches Phänomen ist die Kelvin-Helmholtz-Instabilität zwischen zwei unterschiedlich schnellen Strömungen oder die Rayleigh-Taylor-Instabilität zwischen zwei unterschiedlich schweren Flüssigkeiten (Abb. 3). Die Durchmischung führt zu einem Ausgleich des Gefälles, es sei denn, äußere Einflüsse halten das Gefälle aufrecht. Dann können andauernde, kreisende Konvektionszellen entstehen (Passatwind, Walker-Zirkulation, Konvektionszone der Sonne, Abb. 4).

Eigenschaften der Drehbewegung

Abb. 5: Ein durch eine theoretische, konstante Auftriebskraft am Tragflügel erzeugter Hufeisenwirbel hinter einem Segelflugzeug

Wirbel bilden oftmals keine stationäre Strömung, können also ihre Form ändern und sich als ganzes fortbewegen. In diesem Fall sind die Wege der Fluidelemente keine geschlossenen Kurven, sondern eher Schraubenlinien oder Zykloide. Die Drehachse der Wirbel, die analog zur Stromlinie definierte Wirbellinie, kann eine gebogene, sich windende und als ganzes bewegende Linie sein (Tornado). Die drehende Bewegung kann mit radialen, zum Zentrum hin oder weg gerichtetem Fluss kombiniert sein, was zu Strudeln und Spiralen wie bei Abflüssen führt. Ein rein kreisender Wirbel ohne radiale Geschwindigkeitskomponente wird quellenfrei genannt.

Wegen der Drehimpulserhaltung können Wirbel nicht ohne weiteres aufhören oder beginnen zu drehen. Einmal aufgelöste Wirbel bleiben verschwunden, was die Aussage des ersten Helmholtz’schen Wirbelsatzes ist. Die Kreisbewegung (Zirkulation) eines Rings aus Fluidelementen ist eine Erhaltungsgröße (Kelvinscher Wirbelsatz), die über die Länge einer Wirbelröhre konstant ist (dritter Helmholtz’scher Wirbelsatz). Daher neigen Wirbel dazu ausgedehnte Wirbelröhren im Fluid auszubilden, was beispielsweise am Hufeisenwirbel deutlich wird, siehe Abb. 5. Durch Reibeffekte und Dissipation lösen sich jedoch reale Wirbel mit der Zeit auf und nimmt die Zirkulation in Wirbeln ab.

Die Fluidelemente werden vom Wirbel mitgeführt, was eine Konsequenz des zweiten Helmholtz’schen Wirbelsatzes ist. So können Wirbel Masse, Drehimpuls und Energie über beachtliche Entfernungen, die das mehrfache ihrer Größe betragen können, mit nur geringen Verlusten transportieren (Rauchringe).

In größeren Wirbeln drehen sich die Fluidelemente nicht um sich selbst, sondern werden im Kreis parallel verschoben. Diese Tatsache führt zwischen den Fluidelementen zu Scherungen, die zum Zentrum des Wirbels hin zunehmen. Viskosität verringert diese Scherung im Zentrum des Wirbels oder in kleinen Wirbeln, so dass es dort zu einer quasi-starren Rotation kommt. Diese Reibeffekte dissipieren die Rotationsenergie und führen letztendlich zur Auflösung der Wirbel (siehe Energiekaskade turbulenter Strömungen und #Rankine-Wirbel unten).

Druck- und Temperaturverteilung in Wirbeln

Abb. 6: Kondensation von Wasserdampf im Zentrum von Wirbeln hinter einer Boeing B-747.

In einem Fluid mit niedriger Viskosität ist in einer stationären Strömung bei Vernachlässigung äußerer Kräfte die Summe aus kinetischer Energie und dem statischen Druck, der Totaldruck, entlang einer Stromlinie konstant. Der statische Druck, ist der Druck, den ein mit der Strömung mitbewegtes Fluidelement verspürt. In größeren Wirbeln nimmt die Strömungsgeschwindigkeit zum Zentrum hin zu, weswegen der statische Druck dort abnimmt. In einem realen Gas geht in einem konstanten Volumen abnehmender Druck mit abnehmender Temperatur einher, weshalb im Zentrum der Wirbel die Temperatur am niedrigsten ist. Daher ist das Zentrum solcher Wirbel auf Grund von Kondensstreifen manchmal sichtbar, siehe Abb. 6. Die Wirbelstärke ist in den Randwirbeln an den Flügelspitzen am größten und dort bilden sich klar umrissene Wirbelröhren. Die Intensität der Wirbelröhren nimmt zum Rumpf hin ab und die Wirbelröhren sind weniger klar definiert.

Wirbel und Turbulenz

Wirbel sind der Hauptbestandteil turbulenter Strömungen aber nicht jeder Wirbel gehört zu einer turbulenten Strömung. Turbulente Strömungen beinhalten auf allen Größenskalen Wirbel, die sich scheinbar ungeordnet bewegen. Eine in der Praxis bewährte Unterscheidung wird bei den Reynolds-Gleichungen getroffen: Die physikalischen Größen – hier interessiert vor allem die Geschwindigkeit – werden in einen Mittelwert und einen statistischen Schwankungswert aufgeteilt. Der Schwankungswert behandelt die zufälligen, fluktuierenden Wirbel während der zeitunabhängige Mittelwert die stationären Wirbel beinhaltet.

Abb. 7: Animation zur Ausbildung einer Wirbelstraße

Ein Grenzfall sind periodische Ablösungen von Wirbeln wie in der Kármánschen Wirbelstraße, die hinter einem umströmten Zylinder bei nicht zu großer Reynoldszahl entsteht, siehe Animation in Abb. 7. Hinter dem zunächst laminar, wirbelfrei umströmten Zylinder bildet sich bei zunehmender Strömungsgeschwindigkeit ein stationärer Wirbelring, der von der äußeren Strömung zunächst noch laminar umflossen wird. Der Wirbelring wächst mit der Reynoldszahl, bis er schließlich instabil wird und sich periodische Ablösungen bilden: Es lösen sich in einem charakteristischen Muster abwechselnd links- und rechts-drehende Wirbel ab. Diese Wirbel sind weder stationär noch chaotisch fluktuierend. Mit steigender Anströmungsgeschwindigkeit geht die Wirbelstraße in turbulente Strömung über: Es treten mehr Wirbel auf, so dass der Strömungswiderstand ansteigt. Beim Übergang zur Turbulenz variieren die Größe der Wirbel und die Zeitpunkte ihrer Ablösung immer mehr. Bei voll ausgebildeter Turbulenz sind Wirbel auf allen Größenskalen vorhanden. Bei einer Reynoldszahl Re ≈ 3·10⁵ wird auch die Grenzschicht turbulent und der Widerstand fällt abrupt ab um dann wieder anzusteigen[2], siehe Abhängigkeit des Strömungswiderstandes.

Dieser Übergang von laminarer, wirbelfreier Strömung in turbulente Strömung mit einem Übergangsbereich, der deutliche Strukturen aufweist, ist ein weit verbreitetes Phänomen.

Wirbeltypen

Potentialwirbel

Abb. 8: Potentialwirbel mit Stromlinien (blau) und Fluidelementen (Türkis)

Der Potentialwirbel oder freie Wirbel ist ein klassisches Beispiel einer rotationsfreien Potentialströmung, siehe Abb. 8. Große Wirbel in Fluiden mit niedriger Viskosität werden mit diesem Modell gut beschrieben. Beispiele für einen Potentialwirbel sind der Badewannenablauf fern des Ausflusses, aber auch in guter Näherung ein Tornado. Die Winkelgeschwindigkeit in diesen Wirbeln ist in ihrem Zentrum am größten wo andererseits der Druck im Minimum ist. Wegen dieser, von einer Starrkörperbewegung abweichenden Geschwindigkeitsverteilung werden die Fluidelemente verformt.

Weil die Rotation „rot“ des Geschwindigkeitsfeldes ${\vec {v}}$ gemäß

|\operatorname {rot} \,{\vec {v}}|=0

verschwindet, zeigen die Fluidelemente trotz ihrer kreisenden Bewegung im Wirbel immer in dieselbe Richtung. Wenn man mathematisch genau ist, gilt die obige Gleichung allerdings nur außerhalb des Zentrums, also für $(x,y)\neq \operatorname {0} ,$ während bei Mitnahme des Zentrums $\operatorname {rot} \,{\vec {v}}={\vec {\Phi }}_{0}\cdot \delta (x,y)$ gilt, mit der zweidimensionalen Diracschen Deltafunktion und der Wirbelstärke ${\vec {\phi }}_{0}.$

Wegen dieser totalen Rotationsfreiheit für alle Punkte außerhalb des Zentrums kann lokal nicht auf eine Wirbelbewegung geschlossen werden. Erst die Beobachtung eines größeren Gebietes oder über längere Zeiträume gestattet es, diese Wirbel zu erkennen. In der numerischen Strömungsmechanik ist das kleinste betrachtete Volumen das finite Volumen für das sogenannte Wirbelkriterien formuliert wurden, um Wirbel von Scherschichten zu unterscheiden.

Festkörperwirbel

Abb. 9: Festkörperwirbel mit Stromlinien (blau) und Fluidelementen (Türkis)

Ein Festkörperwirbel bildet sich z. B. wenn sich nach entsprechend langer Anlaufzeit eine Flüssigkeit in einem Gefäß auf einem Drehteller mit konstanter Winkelgeschwindigkeit $\omega$ als starrer Körper dreht, siehe Abb. 9. Mitbewegte Fluidteilchen drehen sich um ihre eigene Achse, ohne verformt zu werden. In einem Festkörperwirbel ist

|\operatorname {rot} \,{\vec {v}}|=2\omega \neq 0\,.

Alle Fluidpartikel bewegen sich wie beim Potentialwirbel auf konzentrischen Kreisbahnen, aber die Geschwindigkeits- und Druckverteilung ist eine völlig andere: Die Geschwindigkeit ist außen am größten und innen am langsamsten, so dass der Druck außen am niedrigsten und innen am höchsten ist.

Rankine-Wirbel

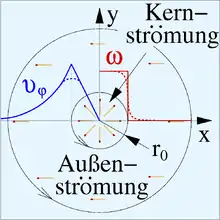
Abb. 10: Skizze eines Rankine-Wirbels

Der Rankine-Wirbel[3] nach William John Macquorn Rankine ist ein Wirbelmodell, das den Potentialwirbel im Außenbereich mit dem Festkörperwirbel im Zentrum verbindet, siehe Abb. 10. Der Potentialwirbel beschreibt eine Ausflussströmung im Außenbereich gut, wo die Umfangsgeschwindigkeit $v_{\varphi }$ mit dem Radius abnimmt (blaue Kurve) und keine Rotation vorliegt ( $\omega =|\operatorname {rot} {\vec {v}}|\,,$ rote Kurve). Mit Annäherung der Fluidelemente an das Zentrum entwickeln sich im Potentialwirbel unrealistisch hohe Schergeschwindigkeiten im Fluid. Im Rankine-Wirbel verhindern Zähigkeitskräfte unterhalb eines gewissen Kernradius r₀ die Scherungen und es kommt zu einer quasi-starren Drehung. Innerhalb des Kernradius ist die Umfangsgeschwindigkeit daher proportional zum Radius und die Rotation ω ist konstant ungleich null. In realen Fluiden wird der Übergang von der Außen- in die Kernströmung nicht abrupt, sondern glatt verlaufen (gestrichelte rote und blaue Kurven). Der Effekt der außen fehlenden und innen vorhandenen Rotation der Teilchen ist durch mitschwimmende Streichhölzer angedeutet.

Hamel-Oseen’scher-Wirbel

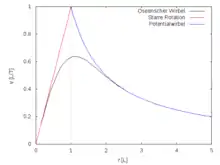
Abb. 11: Umfangsgeschwindigkeit beim Hamel-Oseen’schen-Wirbel im Vergleich mit der starren Rotation und dem Potentialwirbel

Der Hamel-Oseen’sche-Wirbel (von Carl Wilhelm Oseen, Georg Hamel) ist ein Wirbelmodell, das die Navier-Stokes-Gleichungen exakt erfüllt, die die Strömung realer Fluide gut beschreibt. Das Fluid strömt rein kreisförmig jedoch zeitabhängig, instationär um das Wirbelzentrum. Die Viskosität zehrt die kinetische Energie des Wirbels mit der Zeit auf und die Strömungsgeschwindigkeit nimmt monoton mit der Zeit ab. Zu Beginn der Bewegung oder im Grenzfall verschwindender Viskosität ist der Wirbel ein Potentialwirbel. Ansonsten ist das Geschwindigkeitsprofil des Hamel-Oseen’schen-Wirbels beschränkt und entspricht im Wirbelkern, sowie im Außenbereich einem Rankine-Wirbel, siehe Abb. 11.

Weblinks

Wiktionary: Wirbel – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Einzelnachweise

Luftblattvisualisierung an einer offenen Pfeife, aufgerufen am 27. August 2015.
J. H. Spurk: Strömungslehre. Einführung in die Theorie der Strömungen. 8. überarbeitete Auflage. Springer Verlag, Heidelberg, Dordrecht, London, New York 2010, ISBN 978-3-642-13142-4, S. 377 f., doi:10.1007/978-3-642-13143-1 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 3. Januar 2021]).
H. E. Siekmann, P. U. Thamsen: Strömungslehre. Springer, 2007, ISBN 978-3-540-73726-1, S. 177 f.

Literatur

M. Bestehorn: Hydrodynamik und Strukturbildung. Springer, 2006, ISBN 978-3-540-33796-6.
Hans J. Lugt: Wirbelströmung in Natur und Technik. Braun Karlsruhe, 1979, ISBN 3-7650-2028-1.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Luftblattvisualisierung an einer offenen Pfeife, aufgerufen am 27. August 2015.

[2] J. H. Spurk: Strömungslehre. Einführung in die Theorie der Strömungen. 8. überarbeitete Auflage. Springer Verlag, Heidelberg, Dordrecht, London, New York 2010, ISBN 978-3-642-13142-4, S. 377 f., doi:10.1007/978-3-642-13143-1 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 3. Januar 2021]).

[3] H. E. Siekmann, P. U. Thamsen: Strömungslehre. Springer, 2007, ISBN 978-3-540-73726-1, S. 177 f.