Düse
Eine Düse ist eine technische Vorrichtung zur Beeinflussung eines Fluids beim Übertritt von einer Rohrströmung in den freien Raum, sie bildet dabei den Abschluss der Rohrleitung. Die Düse kann auf ihrer gesamten Länge die gleiche Querschnittsfläche haben, sich erweitern, verjüngen oder weitere komplexe Formen aufweisen. Die Düse verrichtet keine Arbeit, sondern wandelt zwischen Geschwindigkeit und statischem Druck.
Durch eine Düse kann
- ein Fluid entlang eines Druckgefälles beschleunigt,
- eine feste oder zähflüssige Masse geformt (siehe Extruder) oder
- eine flüssige Substanz zerstäubt
werden.
Typen und Anwendungen
Spinndüsen
Spinndüsen sind meist runde oder eckige Platten aus Glas, Metall oder Keramik mit mehreren, gleich großen Öffnungen. Manchmal haben sie auch die Form von Zylindern oder Kegeln. Sie sollen die Spinnmasse in gleiche Spinnschmelze- bzw. Spinnlösungsstrahlen aufteilen.
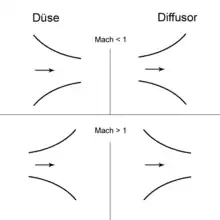
Konfusor / Diffusor
Ein Konfusor ist das Gegenstück eines Diffusors. In einem Konfusor erhöht sich die Geschwindigkeit des Fluids (flüssig oder gasförmig), im Diffusor wird das durchströmende Fluid abgebremst. Die Geometrie von Konfusor und Diffusor hängt dabei von der Mach-Zahl des strömenden Fluids ab. Während bei Unterschallgeschwindigkeit ein sich verjüngender Querschnitt als Konfusor und ein sich erweiternder Querschnitt als Diffusor wirkt, ist die Beziehung bei Überschallgeschwindigkeit umgekehrt.
Turbinentriebwerk
Ein komplexes Anwendungsbeispiel für eine Düse ist das Strahltriebwerk in einem Strahlflugzeug. Die Luft darf die inneren Bauteile nur im Unterschallbereich umströmen, da es sonst zu einem Strömungsabriss an den Schaufeln der Rotoren und Statoren kommen würde. Der Brennkammer würde in diesem Fall nicht genug Sauerstoff zugeführt werden und der Antrieb ausfallen. Um dies zu verhindern, schaltet man für den Überschallflug einen Diffusor vor das Triebwerk. Vor dem Austritt des Luftstromes muss dieser wieder auf Überschallgeschwindigkeit beschleunigt werden. Das geschieht mit Hilfe der Düse.
In einer Düse stellen nicht nur der Querschnitt und die Fließgeschwindigkeit, sondern auch die Dichte bzw. der kinetische Druck des Fließmediums eine Kennzahl dar. Diese Kennzahlen sind proportional voneinander abhängige Werte. Daraus ergibt sich, dass sich die Querschnittsfläche der Düse im Überschallbereich vergrößern statt verringern muss, um eine höhere Fließgeschwindigkeit zu erreichen.
Der mathematische Zusammenhang lässt sich mit Hilfe der Rankine-Hugoniot-Gleichung (Flächen-Geschwindigkeits-Beziehung) erklären:
- Bei subsonischer Strömung (Unterschallfließgeschwindigkeit) bewirkt eine Querschnittsabnahme einen Geschwindigkeitszuwachs. Eine subsonische Düse ist demnach konvergent (in Fließrichtung verjüngend) geformt.
- Für eine supersonische bzw. hypersonische Strömung (Überschallfließgeschwindigkeit) bewirkt eine Querschnittszunahme einen Geschwindigkeitszuwachs. Eine entsprechende hypersonische/supersonische Düse ist demnach divergent geformt. Die Dichte nimmt bei einer Überschallströmung schneller ab, als die Strömungsgeschwindigkeit zunimmt.
- Bei einer transsonischen Strömung ist , denn sonst hat die Gleichung keine Lösung, das heißt im engsten Querschnitt der Düse ist die Mach-Zahl Ma = 1.

Die auf dem Bild sichtbare Düse des Raketenantriebes wird „von oben nach unten“ durchströmt und stellt ein Beispiel für eine hypersonische und somit divergente Düse dar.
Siehe auch
- Düsenströmung für mathematische Zusammenhänge
- Zerstäubungstechnik – Düsen und Vernebler zur Zerstäubung
- Lavaldüse bei vielen Raketen
- Luftklinge eine flache Düse
- Feuerung (Düsenauswahl für Heizölbrenner)
- Venturi-Düse als Drossel
- Messblende (Durchflussbegrenzer/messer)
Literatur
- G. K. Batchelor: An introduction to fluid mechanics. Cambridge university press, ISBN 0-521-66396-2.
- D. Meschede (Hrsg.): Gerthsen Physik. Springer Verlag, Berlin, ISBN 3-642-12893-9.