Magnetohydrodynamik

Die Magnetohydrodynamik (MHD) ist ein Teilgebiet der Physik. Sie beschreibt das Verhalten elektrisch leitender Fluide, die von magnetischen (und elektrischen) Feldern durchdrungen werden.

Die Magnetohydrodynamik im engeren Sinne behandelt Flüssigkeiten, insbesondere auch Plasmen (Magnetoplasmadynamik, MPD), die im Rahmen der MHD als Flüssigkeiten (Fluide) beschrieben werden. Die Magnetogasdynamik (MGD) dagegen behandelt Gase.

Die mathematische Behandlung erfolgt durch eine Kombination der Navier-Stokes-Gleichungen der Hydrodynamik mit den Maxwell-Gleichungen der Elektrodynamik.

Typische Anwendungsgebiete der MHD sind die Strömungsbeeinflussung und die Strömungsmessung in Metallurgie und Halbleiter einkristall züchtung sowie die Beschreibung von Plasmen in stellaren Atmosphären und Fusionsreaktoren.

Theorie

Um die Dynamik eines Plasmas in allen Einzelheiten zu beschreiben, wäre es nötig, die Bewegungsgleichung für jedes Teilchen zu lösen. Natürlich ist dieser Ansatz unsinnig, da die Zahl der Teilchen im Allgemeinen sehr groß ist. Um das Problem trotzdem lösen zu können, wählt man einen statistischen Ansatz. Das heißt in der Praxis, dass man, anstatt die Trajektorien der Einzelteilchen zu betrachten, makroskopische Größen (Mittelwerte) verwendet.

Ein Beispiel für eine solche Größe ist die Fließgeschwindigkeit eines Flusses. Insgesamt bewegt sich das Flusswasser in einer Richtung auf das Meer zu. Jedes einzelne Wassermolekül kann sich dabei aber durchaus „kreuz und quer“ bewegen, da es andauernd mit anderen Molekülen wechselwirkt. Entscheidend für das makroskopische Verhalten ist nur, dass die mittlere Geschwindigkeit der Fließgeschwindigkeit entspricht. Mit solchen makroskopischen Größen wie Geschwindigkeit und Druck lassen sich dann alle Phänomene der Schifffahrt adäquat beschreiben, ohne dass jemals ein einzelnes Molekül ins Spiel kommt.

So ähnlich ist es auch bei der MHD. Auch sie ist im Grunde eine hydrodynamische Theorie in dem Sinne, dass Plasmen ähnlich behandelt werden wie Flüssigkeiten. Auch hier werden keine Einzelteilchen, sondern „gemittelte Größen“ behandelt. Die MHD vereinigt Elemente der Hydro- und Elektrodynamik um eine Theorie „elektrisch leitender Plasmen“ zu formen.

Üblicherweise werden noch einige weitere Näherungen gemacht. Das sind erstens elektrische Neutralität, zweitens die Gültigkeit des ohmschen Gesetzes und drittens Quasigleichgewicht. Die letzte Näherung bedeutet, dass das Plasma sich zwar entwickelt, aber langsam im Vergleich zu der Zeit in der sich Gleichgewicht einstellt. Diese Annahme stellt eine große Vereinfachung für die Gleichungen dar, da sie zum Beispiel dafür sorgt, dass der Druck als skalare Größe behandelt werden kann, während man es im Allgemeinen mit einem (richtungsabhängigen) Tensor zu tun hat. Die elektrische Neutralität eliminiert die Ladungsdichte aus den Gleichungen. Unter diesen Voraussetzungen können nun die Gleichungen der MHD formuliert werden.

Die MHD-Gleichungen

Die Grundgleichungen der MHD lauten (in CGS-Einheiten) wie folgt:

{\begin{matrix}\partial _{t}\rho +\nabla \cdot (\rho \mathbf {v} )&=&0&(1)\\[2ex]\rho \partial _{t}\mathbf {v} +\rho (\mathbf {v} \cdot \nabla )\mathbf {v} +\nabla p&=&{\dfrac {\mathbf {J} \times \mathbf {B} }{c}}+\rho \mathbf {g} +\mathbf {F} &(2)\\[2ex]\nabla \times \mathbf {B} &=&{\dfrac {4\pi }{c}}\,\mathbf {J} &(3)\\[2ex]\nabla \times \mathbf {E} &=&-{\dfrac {1}{c}}\,\partial _{t}\mathbf {B} &(4)\\[2ex]\nabla \cdot \mathbf {B} &=&0&(5)\\[2ex]\mathbf {J} &=&\sigma \left(\mathbf {E} +{\dfrac {\mathbf {v} \times \mathbf {B} }{c}}\right)\;&(6)&\end{matrix}}

Die vorkommenden Größen sind die Massendichte $\rho$ , die Plasmageschwindigkeit $\mathbf {v}$ , der Druck $p$ , der elektrische Strom $\mathbf {J}$ , das Magnetfeld $\mathbf {B}$ , das elektrische Feld $\mathbf {E}$ , die Gravitationsbeschleunigung $\mathbf {g}$ und die Lichtgeschwindigkeit $c$ . In Gleichung (2) wurde die Gravitation explizit berücksichtigt; der Term $\mathbf {F}$ deutet an, dass im Allgemeinen weitere Kräfte wie z. B. Reibungskräfte berücksichtigt werden müssen, die hier nicht explizit angegeben wurden. Gleichung (1) beschreibt die Massenerhaltung, Gleichung (2) ist die „Bewegungsgleichung“ oder auch „Impulsgleichung“, die Gleichungen (3), (4) und (5) stammen aus der Elektrodynamik (Maxwell-Gleichungen), wobei in Gleichung (3) der Verschiebungsstrom vernachlässigt wurde. Gleichung (6) ist das ohmsche Gesetz mit der elektrischen Leitfähigkeit, $\sigma$ . Dies ist die einzige Gleichung in der relativistische Effekte berücksichtigt werden.

Um das Gleichungssystem zu schließen, wird noch eine weitere Gleichung benötigt. Dieses kann zum Beispiel die Zustandsgleichung der Materie oder die Gleichung der lokalen Energieerhaltung sein.

Die Gleichungen der MHD können auf unterschiedliche Arten hergeleitet werden. Eine Möglichkeit ist von der Boltzmann-Gleichung auszugehen, um zum obigen Ergebnis zu kommen.

Die Induktionsgleichung

Durch die Kombination der Gesetze von Ampère, Faraday und Ohm (Gleichungen 3, 4 und 6) erhält man die sogenannte Induktionsgleichung.

\partial _{t}\mathbf {B} =\nabla \times (\mathbf {v} \times \mathbf {B} )+\eta \Delta \mathbf {B} \;.

In der Gleichung bezeichnet $\eta =c^{2}/(4\pi \sigma )=1/(\mu _{0}\sigma )$ die magnetische Diffusivität. Diese Gleichung spielt eine wichtige Rolle für das Verständnis magnetischer Plasmen.

Ideale MHD

Die Lösung der MHD Gleichungen kann sehr kompliziert werden. In vielen Fällen können die Gleichungen jedoch durch weitere Annahmen vereinfacht werden, um ihre Lösung zu erleichtern. Nimmt man an, dass die elektrische Leitfähigkeit des Plasmas unendlich groß ist ( $\sigma =\infty$ ), es daher also keinen elektrischen Widerstand besitzt, nennt man die resultierende Theorie „Ideale MHD“ im Gegensatz zur „resistiven MHD“ mit endlicher Leitfähigkeit. Im idealen Fall liefert Gleichung (6) $\mathbf {E} \cdot c=-\mathbf {v} \times \mathbf {B}$ .

Beispiele für die Anwendbarkeit der Idealen MHD finden sich zum Beispiel bei der Berechnung von Plasmaströmungen in Zusammenhang mit der Kernfusion oder stellaren Koronen. Zusätzlich wird oft angenommen, dass das Plasma inkompressibel ist (also $\partial _{t}\rho =0$ ) und es keine innere Reibung (Viskosität) gibt.

Eingefrorenes magnetisches Feld

Die MHD kombiniert die hydro- und elektrodynamischen Eigenschaften von Plasmen. Somit sind Materialbewegungen und das Verhalten des Magnetfeldes nicht unabhängig voneinander. Plasmabewegungen führen zu weiteren magnetischen und elektrischen Feldern, die im Inneren des Plasmas wiederum zu elektrischen Strömen führen.

Ein wichtiger Spezialfall ergibt sich für den Fall der Idealen MHD. Hier verschwindet der elektrische Widerstand des Plasmas und die Induktionsgleichung nimmt die Form

\partial _{t}\mathbf {B} =\nabla \times (\mathbf {v} \times \mathbf {B} )

an. Man kann zeigen, dass in diesem Falle Plasma und Magnetfeld gekoppelt sind; das Magnetfeld folgt den Plasmaströmungen. Man spricht in diesem Falle von einem „eingefrorenen“ Magnetfeld oder, im Zusammenhang mit der idealen Induktionsgleichung, auch von einer „flusserhaltenden“ Gleichung. Die Morphologie des Magnetfeldes kann auch in diesem Falle beträchtlichen Änderungen unterworfen sein, es ist aber wichtig, dass keine topologischen Änderungen (daher keine Änderungen im Zusammenhang des Magnetfeldes) vorkommen können.

Ob dabei das Magnetfeld dem Plasma oder das Plasma dem Magnetfeld folgt, hängt davon ab, welche Komponente dominiert, daher einen größeren Druck ausübt. In der Sonne können beide Fälle beobachtet werden. Während das Plasma in der Photosphäre sehr dicht ist und die Plasmabewegungen aus der Konvektionszone das Verhalten des Magnetfeldes dominieren, ist das Plasma in der Korona sehr dünn, so dass die Struktur der Korona vom Magnetfeld dominiert wird.

MHD-Wellen

Im Inneren des Plasmas können sich verschiedene Wellenmoden ausbilden. Dieses sind die langsamen und schnellen magnetoakustischen Wellen und die so genannten Alfvén-Wellen. Diese Moden stellen Spezialfälle für Wellen dar, die sich entweder parallel oder senkrecht zum Magnetfeld ausbreiten. Sie geben Einblick in die grundlegenden physikalischen Phänomene. Im allgemeinen Fall wird man es jedoch mit einer Überlagerung aller Moden zu tun haben.

Anwendungen

Die MHD findet vielfältige Anwendungen sowohl im ingenieurtechnischen als auch im naturwissenschaftlichen Bereich.

Geo- und Sonnendynamo

Das Magnetfeld der Erde wird durch den sogenannten Geodynamo erzeugt, der durch die Gleichungen der Magnetohydrodynamik beschrieben wird. Das Erdmagnetfeld entsteht im äußeren Erdkern, der vorwiegend aus flüssigem Eisen besteht (siehe Entstehung und Aufrechterhaltung des Erdmagnetfeldes (Geodynamo)).

Die im Zusammenhang mit einem Geodynamo auftretenden partiellen Differentialgleichungen können nur in stark vereinfachten Fällen analytisch gelöst werden. Numerische Verfahren liefern seit Mitte der 1990er Jahre erste Ansätze zum Verständnis der Dynamik des Erdmagnetfeldes.

Ähnlich verhält es sich mit dem Magnetfeld der Sonne und anderer Sterne ähnlichen Spektraltyps. Die Entstehung ihrer Magnetfelder resultiert aus dem Zusammenspiel mehrerer Faktoren in den äußeren Schichten der Sterne (Dynamotheorie) und wird ebenfalls mit auf der MHD beruhenden Modellen beschrieben.

Stellare Atmosphären

Die Korona (äußerste Atmosphäre) der Sonne und anderer Sterne ist ein hochstrukturierter Bereich sehr niedriger Plasmadichten in dem das Magnetfeld die dominierende, strukturgebende Komponente darstellt. MHD-Effekte sind hier sehr wichtig, um die Aufteilung und Dynamik dieser äußeren Sternatmosphäre zu beschreiben und zu verstehen. Auch in den darunterliegenden atmosphärischen Schichten der Chromosphäre und der Photosphäre spielt die MHD eine wichtige Rolle.

Elektromagnetische Strömungsbeeinflussung

Magnetfelder werden in der Metallurgie eingesetzt, um die Strömung von Flüssigmetallen wie beispielsweise Stahl oder Aluminium zu beeinflussen. Bei der Anwendung ist zwischen statischen und zeitabhängigen Magnetfeldern zu unterscheiden. Statische (zeitunabhängige) Magnetfelder führen zu einer Dämpfung von Turbulenz und werden deshalb in Form magnetischer Bremsen (englisch: electromagnetic brakes) beim Stranggießen von Stahl eingesetzt. Zeitabhängige Magnetfelder finden Anwendung zum elektromagnetischen Abstützen beim Gießen von Aluminium (elektromagnetisches Gießen).

Optimierung elektrochemischer Prozesse

Die Beeinflussung elektrochemischer Anwendungen durch ein Magnetfeld wird Magnetoelektrochemie genannt. Durch dieses wird aufgrund der MHD bei Stromfluss eine Konvektionsströmung im Elektrolyten hervorgerufen. So lassen sich bei Elektrolysen höhere Stromdichten erreichen, beispielsweise bei der Metallabscheidung.

Elektromagnetische Strömungsmessung

Bewegt sich ein elektrisch leitfähiges Fluid unter dem Einfluss eines Magnetfeldes, so wird in dem Fluid eine Spannung erzeugt, die der Stärke des Magnetfeldes und der Strömungsgeschwindigkeit proportional ist. Dieses Prinzip wurde 1832 von Michael Faraday entdeckt, der auf diese Weise (erfolglos) versuchte, die Fließgeschwindigkeit der Themse zu bestimmen. Das Prinzip findet heute in Gestalt von elektromagnetischen Durchflussmessern (auch induktive Durchflussmesser genannt), breitgefächerte Anwendung in Lebensmittelindustrie, der chemischen Industrie sowie in Wasserwerken. Bei der Bewegung eines elektrisch leitfähigen Fluids in einem Magnetfeld entstehen in dem Fluid auf Grund der induzierten Spannung auch Wirbelströme. Diese erzeugen im Fluid eine Lorentzkraft, die der Bewegung entgegenwirkt. Dieser physikalische Effekt wird in dem als Lorentzkraft-Anemometrie bezeichneten berührungslosen Strömungsmessverfahren angewendet.

MHD-Generator

Eine technische Anwendung der Magnetohydrodynamik ist der magnetohydrodynamische Generator (MHD-Generator). Hierbei wird ein Plasma zwischen zwei leitenden Elektroden hindurchgeschossen. Senkrecht zu den Elektroden wird ein Magnetfeld angelegt, das dann die negativ geladenen Elektronen und die positiv geladenen Ionen auf Grund der gegensätzlichen Ladung trennt. Zwischen den Platten entsteht somit eine Spannungsdifferenz. Auf diese Weise kann kinetische Energie direkt in elektrische Energie umgewandelt werden, ohne mechanische Komponenten (Turbinen oder Generatoren) benutzen zu müssen. Trotz intensiver Anstrengungen, insbesondere in den 1960er Jahren, ist es nicht gelungen, langzeitstabile Elektroden zu entwickeln. Aus diesem Grunde besitzt der MHD-Generator gegenwärtig keinerlei praktische Bedeutung.

MHD-Antrieb

Eine elektrisch leitfähige Substanz, wie zum Beispiel ein Plasma, kann in einem elektromagnetischen Feld beschleunigt werden (Magnetoplasmadynamischer Antrieb). Da auch Meerwasser und ionisierte Luft als Ionengemische leitfähig sind, können sie ebenfalls in einem elektromagnetischen Feld beschleunigt werden (Magnetohydrodynamischer Antrieb). Diese Eigenschaften können im Prinzip zum Antrieb von Schiffen, U-Booten und Fluggeräten genutzt werden. Der Wirkungsgrad solcher Anlagen ist jedoch gering. Aus diesem Grund besitzt der MHD-Antrieb heute keine praktische Bedeutung.

MHD-Sensor

MHD-Sensor

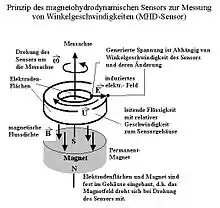
Magnetohydrodynamische Sensoren werden genutzt, um Winkelgeschwindigkeiten zu messen. Die Genauigkeit steigt mit der Größe. Ein Einsatzgebiet ist die Luft- und Raumfahrt. Das Prinzip eines MHD-Sensors, das auch die prinzipielle Idee der Magnetohydrodynamik (MHD) insgesamt verstehen hilft, ist in dieser Skizze dargestellt.

Siehe auch

Weblinks

Literaturhinweise

Eugene N. Parker: Cosmical Magnetic Fields: Their Origin and their Activity. Oxford University Press, Oxford 1979. ISBN 978-0-19-851290-5.
Arnold O. Benz: Plasma Astrophysics – Kinetic Processes in Solar and Stellar Coronae. 1993, ISBN 0-7923-2429-3.
J. P. Goedbloed: Principles of magnetohydrodynamics – with applications to laboratory and astrophysical plasmas. Cambridge Univ. Press, Cambridge 2004, ISBN 0-521-62347-2.
Peter A. Davidson: An introduction to magnetohydrodynamics. Cambridge Univ. Press, Cambridge 2006, ISBN 978-0-521-79487-9.
C. G. Campbell: Magnetohydrodynamics in binary stars. Kluwer, Dordrecht 1997, ISBN 0-7923-4606-8.
Leonard F. Burlaga: Interplanetary magnetohydrodynamics. Oxford Univ. Pr., New York 1995, ISBN 0-19-508472-1.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.