Srinivasa Ramanujan

Srinivasa Ramanujan, FRS (tamilisch: ஸ்ரீனிவாஸ ராமானுஜன், sriːniˈʋaːsə raːˈmaːnudʒən; auch Srinivasa Ramanujan Iyengar; * 22. Dezember 1887 in Erode; † 26. April 1920 in Chetpet, Madras) war ein indischer Mathematiker. Er eignete sich seine mathematischen Kenntnisse autodidaktisch aus Fachliteratur an und besaß eine außerordentliche Begabung dafür, analytische und zahlentheoretische Probleme intuitiv zu lösen, meist ohne zunächst einen Lösungsweg oder Beweise angeben zu können.

Srinivasa Ramanujan

Ramanujans Unterschrift

Das Patronym Srinivasa wurde von Ramanujan meist mit S. abgekürzt. Ramanujan war sein Rufname. Der Nachname Iyengar, der gleichzeitig die Kastenzugehörigkeit angibt, ist optional. Ramanujan bedeutet „der kleinere Bruder (anuja) von Rama“, dieser Name wurde auch in Hinblick auf Ramanuja gewählt.[1]

In der Schule wurden seine mathematischen Fähigkeiten gefördert, doch ein Studium scheiterte daran, dass er nichtmathematische Fächer vernachlässigte. Am Existenzminimum lebend, betrieb er die Mathematik privat und notierte seine Erkenntnisse in sogenannten „Notizbüchern“. Versuche einer wissenschaftlichen Anerkennung blieben zunächst ohne Erfolg, bis der britische Mathematiker Godfrey Harold Hardy im Jahr 1913 sein Talent erkannte und ihn nach England holte, wo ihm zahlreiche bedeutende Entdeckungen gelangen. Sechs Jahre später kehrte Ramanujan als bekannter Wissenschaftler nach Indien zurück und starb 1920 im Alter von nur 32 Jahren. Er hatte zeitlebens mit gesundheitlichen Problemen zu kämpfen.

Leben

Geburtshaus von Ramanujan in Erode, Alahiri Street

Ramanujans Wohnhaus in der Sarangapani Street in Kumbakonam

Der Gopuram des Sarangapani-Tempels in Kumbakonam, in dessen Nähe Ramanujan aufwuchs. Die Straße, in der das Wohnhaus seiner Eltern lag, führte direkt auf den Tempel zu.

Höhere Oberschule in Kumbakonam, die Ramanujan besuchte. Eine Halle dort ist nach Ramanujan benannt.

Jugend und Ausbildung

Srinivasa Ramanujan wurde am 22. Dezember 1887 in eine Familie orthodoxer tamilischer Brahmanen aus der Kaste der Iyengar geboren.[2] Nach der Geburt in Erode, wo seine Großeltern mütterlicherseits lebten und wo die Mutter traditionell zur Geburt hinging, wuchs er im Wohnort der Eltern (die Mutter kehrte ein Jahr nach der Geburt dorthin zurück)[3] in Kumbakonam zunächst in einem kleinen Haus in der Sarangapani Street auf. Sein Vater K. Srinivasa Iyengar arbeitete als Kontorist in einem Sari-Laden, seine Mutter Komalatammal Srinivasa war eine gebildete Hausfrau und in einem nahegelegenen Tempel als Sängerin von liturgischen Gesängen (Bhajan) tätig. Die Hälfte der Einnahmen ging an den Tempel, die andere Hälfte an die Sänger. Seine Mutter erhielt so monatlich 5 bis 10 Rupien im Vergleich zum Verdienst von monatlich 20 Rupien des Vaters. Die Familie lebte in ärmlichen Verhältnissen und musste häufig die Wohnung wechseln. Drei seiner später geborenen vier Brüder starben im Säuglingsalter. Schon als Kleinkind in Erode fiel er durch Sensibilität und Eigensinnigkeit auf – so wälzte er sich im Schmutz am Boden, wenn er nicht das zu essen bekam, was er wollte. In den ersten drei Lebensjahren sprach er kaum, holte aber schnell auf, als er nach einer traditionellen Methode die Aussprache lernte, indem er die tamilischen Buchstaben unter Anleitung des Großvaters in eine Reisschicht am Boden zeichnete.[4]

Im Dezember 1889 erkrankte Ramanujan schwer an Pocken, die in der Region tausende Menschen das Leben kosteten. Danach ging er mit seiner Mutter in die Stadt Kanchipuram, wohin zuvor seine Großeltern aus Erode gezogen waren.

Am 1. Oktober 1892 kam er im Alter von vier Jahren in die Vorschule und im März 1894 auf die Telugu Medium School. Dann verlor sein Großvater sein Amt als Richter in Kanchipuram, und Ramanujan zog mit seiner Mutter zurück nach Kumbakonam. Dort besuchte er die Kangayan Primary School. Nach dem Tod seines Großvaters väterlicherseits schickte man ihn zu den Großeltern mütterlicherseits, die mittlerweile in Madras (heute Chennai) lebten. Dort mied Ramanujan die Schule und erhielt deshalb einen Aufseher, der den Schulbesuch sicherstellen sollte. Nach sechs Monaten zog er zurück nach Kumbakonam.

Ramanujan entwickelte ein enges Verhältnis zur Mutter, die ihn als Brahmanen erzog und ihm die Traditionen, das Kastenwesen, die Puranas, religiöse Lieder und die Zelebrierung der Puja beibrachte. Sein Vater war nur selten daheim.

Auf der Kangayan Primary School galt Ramanujan kurz vor seinem zehnten Geburtstag in den Fächern Englisch, Tamil, Geographie und Arithmetik als bester Schüler des Distrikts. Anschließend besuchte er die Town High School und fiel bald als Mathematik-Wunderkind auf: Mit seinen elf Jahren war er zwei College-Studenten aus der Nachbarschaft mathematisch überlegen. Bücher über fortgeschrittene Trigonometrie von Sidney Luxton Loney arbeitete er innerhalb von zwei Jahren selbst durch. Allerdings brachten ihn seine Interessen und Fähigkeiten in Gefahr, zum Außenseiter zu werden:

„Als er mit vierzehn in der vierten Klasse war, hatten einige seiner Klassenkameraden bereits begonnen, Ramanujan abzuqualifizieren als einen, der in den Wolken schwebt, als jemanden, mit dem man kaum kommunizieren konnte. ‚Wir (Lehrer und Schüler) verstanden ihn nur selten‘, erinnerte sich ein Mitschüler ein halbes Jahrhundert später. Man kann sich gut vorstellen, daß sich einige Lehrer angesichts seiner Fähigkeiten unwohl fühlten. Aber der größte Teil der Schule hatte vor ihm offenbar ehrfürchtigen Respekt, unabhängig davon, ob sie ihn verstanden oder nicht.“[5]

Im Jahr 1902 erhielt Ramanujan Zertifikate für besondere Verdienste und Auszeichnungen und war der Schulleitung dabei behilflich, die 1200 Schüler auf das 35-köpfige Lehrerkollegium zu verteilen. Er begann sich für unendliche Reihen zu interessieren. Mit 16 Jahren stieß er auf das Buch A Synopsis of Elementary Results in Pure and Applied Mathematics von George Shoobridge Carr mit über 5000 mathematischen Sätzen. Zum Schulabschluss (1904) bekam er für seine mathematischen Leistungen den K. Ranganatha Rao Prize, was ihm ein Stipendium am Government College in Kumbakonam ermöglichte, dem sogenannten „Cambridge Südindiens“. Im Alter von 17 Jahren berechnete Ramanujan die Euler-Mascheroni-Konstante im Kopf auf 15 Stellen hinter dem Komma.

Er begann am Government Arts College in Kumbakonam zu studieren, doch vernachlässigte er die Pflichtfächer Englisch und Sanskrit und verlor deshalb im Januar des Jahres 1905 sein Stipendium wieder,[6] so dass er das Studium abbrechen musste. Im August 1905 zog er nach Visakhapatnam und schrieb sich am Pachaiyappa’s College in Madras ein, musste jedoch auch dieses Studium wegen einer Erkrankung und nicht bestandener Prüfungen aufgeben.[7]

Leben in Indien

Ohne Ausbildung und Anstellung lebte Ramanujan am Existenzminimum und litt oft Hunger. Auf den Wunsch seiner Mutter hin heiratete er am 14. Juli 1909 die erst zehnjährige S. Janaki Ammal (1899–1994), die weiterhin bei ihren Eltern lebte. Wenige Monate später erkrankte er an einer Hydrocele testis, einer Ansammlung von Flüssigkeit in den Hodenhüllen; im Januar 1910 wurde er operiert.

Nach der Genesung nahm Ramanujan eine Stelle als Kontorist in Madras an, daneben gab er Studenten des Presidency College Nachhilfe in Mathematik. Er bewarb sich beim Distriktvorsteher V. Ramaswami Iyer, der kurz zuvor die Indian Mathematical Society (IMS) ins Leben gerufen hatte, mit seinen Notizbüchern mit Formeln um eine Stelle in der Finanzabteilung. Iyer meinte später:

„Ich war beeindruckt von den außergewöhnlichen mathematischen Ergebnissen, die in ihnen [in den Notizbüchern] enthalten waren. [...] Mir kam es nicht in den Sinn, sein Talent durch eine Anstellung auf der untersten Sprosse der Finanzabteilung zu unterdrücken.“[8]

Iyer schickte Ramanujan mit Empfehlungspapieren zu befreundeten Mathematikern nach Madras. Diese empfahlen ihn dem Distriktvorsteher von Nelluru und Sekretär der IMS, R. Ramachandra Rao, weiter. Ramanujan rechnete ihm elliptische Integrale, hypergeometrische Funktionen sowie seine eigene Theorie über divergente Reihen vor, und Ramachandra Rao erkannte seine Brillanz. In Madras führte Ramanujan mit der finanziellen Hilfe Ramachandra Raos seine Arbeiten fort und veröffentlichte in der Zeitschrift der IMS.

Eines der ersten Probleme, die er in dem Heft behandelte, war die Berechnung des Ausdrucks

{\sqrt {1+2{\sqrt {1+3{\sqrt {1+\dotsb }}}}}}.

Er wartete lange Zeit auf eine Lösung durch die Leserschaft, doch es kam keine, so dass er die Lösung selbst präsentierte. Er nutzte dabei die Identität:[9]

x+n+a={\sqrt {ax+(n+a)^{2}+x{\sqrt {a(x+n)+(n+a)^{2}+(x+n){\sqrt {\dotso }}}}}}

Mit $x=2,n=1,a=0$ ergibt sich die Formulierung der Aufgabe sowie die Lösung 3.

Ein weiterer Beitrag im Journal der IMS war die siebzehnseitige Abhandlung Some Properties of Bernoulli’s Numbers, in der er Eigenschaften der Bernoulli-Zahlen beschrieb. Unter anderem stellte er eine Methode vor, $B_{n}$ auf der Grundlage anderer Bernoulli-Zahlen durch Rekursionsrelationen auszurechnen.

Anfangs enthielten Ramanujans Texte allerdings etliche Fehler. Der Herausgeber des Journals, M. T. Narayana Iyengar, Mathematikprofessor am Central College in Bangalore, schrieb dazu:

„Mr. Ramanujans Methoden waren so knapp und neuartig und seine Präsentation so mangelhaft in Klarheit und Präzision, dass Normale [mathematische Leser], an solch intellektuelle Gymnastik nicht gewöhnt, ihm kaum folgen konnten.“[10]

Im Januar des Jahres 1912 trat er eine Stelle im Generalbuchhaltungsbüro von Madras an, wo er einen Monatslohn von 20 Indischen Rupien erhielt. Nun zog auch seine mittlerweile 13-jährige Ehefrau zu ihm. Am 1. März 1912 wechselte er ins Buchhaltungsbüro des Hafenamtes in Madras, sein Monatsgehalt stieg auf 30 Rupien. Die Arbeit fiel ihm leicht und ließ ihm Zeit für Forschungen. Sein Vorgesetzter, Sir Francis Spring, und sein Kollege S. Narayana Iyer, ebenfalls Mitglied der IMS, bestärkten ihn darin.

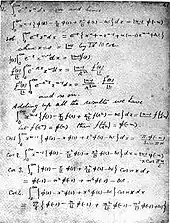
Seite aus Ramanujans „Notebooks“ aus der Zeit zwischen 1903 und 1910

Kontakt mit europäischen Mathematikern

Sir Francis Spring, S. Narayana Iyer, R. Ramachandra Rao und Edward William Middlemast bemühten sich, europäische Mathematiker für Ramanujans Arbeiten zu interessieren. Doch obwohl Micaiah John Muller Hill (1856–1929) vom University College London einräumte, dass Ramanujan „einen Sinn für Mathematik und einiges Talent“ besitze, hielt er dessen Mängel an akademischer Bildung für zu groß, um von besseren Mathematikern akzeptiert zu werden, und beließ es bei Ratschlägen für die Zukunft. Im Jahr 1912 schrieb Ramanujan an Henry Frederick Baker und Ernest William Hobson, zwei führende Mathematiker an der Universität Cambridge. Er bekam seine Unterlagen kommentarlos zurück.

Schließlich wandte er sich brieflich an den international bekannten Mathematiker Godfrey Harold Hardy, der ebenfalls in Cambridge am Trinity College lehrte. Sein neunseitiger Brief vom 16. Januar 1913, voll mit Formeln, begann mit den Worten:[11]

„Sehr geehrter Herr,
ich bitte darum, mich Ihnen vorstellen zu dürfen als Angestellter der Buchhaltung in der Hafenverwaltung von Madras mit einem Jahreseinkommen von £ 20. Ich bin jetzt 26 Jahre alt. Ich habe keine abgeschlossene Universitätsausbildung, habe aber den üblichen Unterricht absolviert. […] Ich habe nicht den konventionellen geregelten Weg beschritten, dem man in einer Vorlesung an der Universität folgt, sondern ich gehe einen eigenen, neuen Weg. [...] Ich bitte Sie, die beigelegten Papiere durchzusehen. Da ich arm bin, möchte ich gerne meine Sätze veröffentlichen, falls Sie überzeugt sind, dass sie einen Wert haben.“[12]

Hardy hielt ihn zunächst für einen Hochstapler. Einige der Formeln waren ihm bekannt, doch die meisten „schienen kaum glaubhaft“. Eine davon stand am Ende der dritten Seite des Briefes:[13][14]

\int _{0}^{\infty }{\cfrac {1+{x}^{2}/({b+1})^{2}}{1+{x}^{2}/({a})^{2}}}\cdot {\cfrac {1+{x}^{2}/({b+2})^{2}}{1+{x}^{2}/({a+1})^{2}}}\cdot \dotsm \;\;{\rm {d}}x={\frac {\sqrt {\pi }}{2}}\cdot {\frac {\Gamma (a+{\frac {1}{2}})\Gamma (b+1)\Gamma (b-a+{\frac {1}{2}})}{\Gamma (a)\Gamma (b+{\frac {1}{2}})\Gamma (b-a+1)}}

für

0<a<b+{\frac {1}{2}}

Hardy glaubte, diese Gleichung, die die Gammafunktion und ein bestimmtes Integral enthielt (ein Gebiet, auf dem er sich für einen Experten hielt), beweisen zu können. Dies gelang ihm später auch, wenn auch die Beweise über bestimmte Integrale in dem Brief allesamt nicht einfach waren. Was Hardy aber vor allem faszinierte, waren die im Brief aufgeführten Resultate über unendliche Reihen, wie etwa

1-5\left({\frac {1}{2}}\right)^{3}+9\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{3}-13\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right)^{3}+\dotsb ={\frac {2}{\pi }}

und

1+9\left({\frac {1}{4}}\right)^{4}+17\left({\frac {1\cdot 5}{4\cdot 8}}\right)^{4}+25\left({\frac {1\cdot 5\cdot 9}{4\cdot 8\cdot 12}}\right)^{4}+\dotsb ={\frac {2^{\frac {3}{2}}}{\pi ^{\frac {1}{2}}\left\lbrace \Gamma \left({\frac {3}{4}}\right)\right\rbrace ^{2}}}.

Das erste Resultat stammt von Gustav Bauer und war aus der Theorie der Legendre-Polynome bereits länger bekannt. Doch das zweite und zwei weitere Resultate waren Hardy völlig neu und stellten seiner Ansicht nach ein sehr viel schwereres Problem dar, als es auf den ersten Blick schien.[15] Sie standen mit der Theorie der hypergeometrischen Funktionen in Zusammenhang, die zuerst von Leonhard Euler und Carl Friedrich Gauß untersucht worden waren. Hardy fand Ramanujans Resultate über unendliche Reihen „sehr viel faszinierender, und es wurde schnell klar, dass Ramanujan weit allgemeinere Sätze besaß und eine Menge zurückhielt.“[16] Die zu ihrem Beweis nötigen Resultate wurden später in einer Monographie von Wilfrid Norman Bailey veröffentlicht.[17] Später fand man auch, dass Ramanujan schon vor 1910 eine Identität kannte (Dougall-Ramanujan-Identität),[18][19] aus der viele solcher Resultate ableitbar waren.

Parthasarathy-Tempel in Madras, Bezirk Triplicane, um 1870. Die Straße, in der Ramanujan vor seiner Abreise nach England wohnte, führte zum Becken des Tempels

Über die Resultate auf der letzten Seite des Briefes, die elliptische Funktionen betrafen, äußerte Hardy:

„Ich hatte zuvor nichts auch nur im Entferntesten Ähnliches zu Gesicht bekommen. Ein einziger Blick darauf genügte, um zu erkennen, dass nur ein Mathematiker allerhöchsten Ranges sie niedergeschrieben haben konnte. Sie mussten wahr sein, denn wären sie das nicht gewesen, so hätte kein Mensch die Phantasie besessen, sie zu erfinden. Schließlich […] musste der Verfasser absolut ehrlich sein, denn große Mathematiker sind häufiger als Diebe und Scharlatane mit einer solch unglaublichen Fähigkeit.“[20]

Hardy zeigte seinem Freund und Kollegen John Edensor Littlewood den Brief Ramanujans. Auch Littlewood versetzten die Leistungen des Inders in Erstaunen. Nach einer Diskussion der beiden Engländer bemerkte Hardy, dass der Brief und die Formeln „sicher das Bemerkenswerteste [sind], das ich je erhalten habe“,[21] und dass Ramanujan „ein Mathematiker von der höchsten Qualität, ein Mann von sowohl außergewöhnlicher Originalität als auch Kraft“[21] sei. Ein weiterer Kollege Hardys, der in Madras lehrende Eric Harold Neville, befand mit Blick auf die Theoreme und Formeln:

„Nicht eines hätte bei der weltweit fortschrittlichsten Untersuchung herausgefunden werden können.“[22]

Hardys briefliche Antwort erreichte Ramanujan am 8. Februar 1913 in Madras. Darin drückte der Brite sein Interesse an der Arbeit des Inders aus:

„Ich fand ihren Brief und ihre Sätze ganz außerordentlich interessant.....Ich wünsche ganz besonders ihre Beweise für diese Behauptungen hier. Sie werden verstehen, dass in dieser Theorie alles von einer rigorosen Exaktheit der Beweise abhängt.“[23]

Schon in den ersten Februartagen, bevor Ramanujan den Brief erhalten hatte, bat Hardy die indischen Behörden, Ramanujans Reise nach Cambridge vorzubereiten. Nach der Ankunft des Briefes setzte sich Arthur Davies, der Sekretär des Advisory Committee for Indian Students, mit dem Inder in Verbindung, um die Überfahrt zu planen, doch dieser lehnte die Einladung nach Großbritannien ab, da er als orthodoxer Brahmane Angst hatte, er würde die Zugehörigkeit zu seiner Kaste verlieren, wenn er in ein fremdes Land ginge. Auch seine Mutter hatte Bedenken. Stattdessen sandte Ramanujan einen weiteren Brief mit Formeln an Hardy, dem er die Worte anfügte:

„Ich habe in Ihnen einen Freund gefunden, der meine Arbeit mit Wohlwollen betrachtet.“[24]

Gilbert Walker, ehemaliger Mathematikprofessor in Cambridge, sah sich Ramanujans Arbeiten an und bat ihn ebenfalls, nach England zu kommen. Auch der indische Mathematiker B. Hanumantha Rao wollte seinen Landsmann dazu überreden. Er lud dessen Arbeitskollegen S. Narayana Iyer zu einem Gespräch der Bildungsbehörde, Fachbereich Mathematik, ein, um herauszufinden, „was wir für S. Ramanujan tun können“. Bei diesem Treffen einigte man sich darauf, Ramanujan ein zweijähriges Forschungsstipendium an der University of Madras zu bewilligen. Pro Monat sollte er 75 Rupien erhalten.

Während seiner Zeit an der Universität veröffentlichte Ramanujan nebenbei weiterhin mathematische Probleme und deren Lösungen in der Zeitschrift der IMS. In dieser Zeit erarbeitete er Wege, bestimmte Integrale leichter zu lösen, überarbeitete die Integraltheorie von Giuliano Frullani aus dem Jahre 1821 und entwickelte Verallgemeinerungen für die Abschätzung zuvor scheinbar unlösbarer Integrale.

Whewell’s Court, Trinity College, Cambridge

Schließlich willigten Ramanujans Eltern in die Reise ein. Am 18. März 1914 (andere Quellen nennen den 17. März) gingen Neville und Ramanujan in Madras an Bord der SS Nevasa und liefen am 18. April in London ein. Ramanujan fand vorübergehend Unterkunft bei Neville in der Chesterton Road in Cambridge. Neville begleitete ihn auch bei seinen ersten Schritten in England in freundschaftlicher Weise.[25] Im Juni bezog Ramanujan Räume am Whewell’s Court des Trinity College,[26] etwa fünf Gehminuten von Hardys Räumen im New Court des Trinity College.[27] Im Oktober 1915 zog er ins Bishop’s Hostel, was sogar noch näher bei Hardy lag. Er blieb meist in Cambridge, auch in den Semesterferien, besuchte aber gelegentlich London, so das Britische Museum und den Zoo, einmal war er in einer Aufführung von Charleys Tante. Wegen seiner vegetarischen Essgewohnheiten nahm er nicht an den gemeinsamen College-Mahlzeiten teil und andere College-Mitglieder sahen ihn eher selten, wenn er etwa in Pantoffeln über den Great Court „watschelte“, da er keine der im Westen üblichen Schuhe trug.[28]

Wissenschaftlicher Erfolg in England

Trinity College (Great Court)

New Court, Trinity College, Cambridge

Ramanujan (Mitte) und Hardy (rechts außen) mit anderen Wissenschaftlern am Trinity College

Unmittelbar nach seiner Ankunft nahm der Inder seine Arbeit auf. Zunächst zeigte er Hardy seine Notizbücher. Zwar hatte er dem Engländer in beiden Briefen zusammen etwa 120 Formeln geschickt, doch die Bücher enthielten noch wesentlich mehr Ansätze, Theoreme und Lösungen. Hardy erkannte, dass einige Rechnungen falsch und andere bereits entdeckt worden waren, doch die Mehrzahl waren neue Durchbrüche. Diese beeindruckten Littlewood und Hardy tief, und Ersterer meinte:

„Ich glaube, dass er mindestens ein Jacobi ist.“[29]

Auch Hardy zog Parallelen zwischen Ramanujan und Jacobi:

„[Ich] kann ihn nur mit Euler oder Jacobi vergleichen.“[30]

Zwischen Ramanujan und Hardy gab es gravierende charakterliche und kulturelle Unterschiede. Der Brite war Atheist und sah sich als Anhänger von Beweisen für Theorien sowie einer gewissen Strenge und Striktheit seiner Wissenschaft. Der Inder dagegen war ein tiefreligiöser Mensch, der zudem während seiner Arbeit vorwiegend auf seine Intuition vertraute und fast nie seine Sätze bewies. Während der gemeinsamen Jahre versuchte Hardy zudem, die Wissens- und Bildungslücken, die Ramanujan in anderen Fachbereichen aufwies, zu füllen, ohne dabei jedoch seine mathematische Inspiration zu beeinträchtigen. Die Zusammenarbeit war intensiv und es war nicht ungewöhnlich, dass Ramanujan dreißig Stunden ununterbrochen arbeitete und dann zwanzig Stunden schlief.[31]

Am 16. März 1916 wurde Ramanujan der Bachelor of Arts by Research aufgrund der Anerkennung seiner Forschungsarbeit verliehen[32] (das entspricht etwa einem Doktortitel; Promotionen kamen in Cambridge erst ab 1917 auf und waren auch danach nicht unbedingt gefordert, wichtiger war die Fellowship eines Colleges), womit vor allem seine Arbeit über hochzusammengesetzte Zahlen gewürdigt wurde, die als Abhandlung in der Zeitschrift der London Mathematical Society erschien.[33] Hardy meinte, diese Berechnungen zählten zu den bis dahin ungewöhnlichsten in der Mathematik, und dass Ramanujan sie mit außerordentlichem Scharfsinn bewältigte. Am 6. Dezember 1917 wählte man Ramanujan in die London Mathematical Society.

Am 18. Februar 1918 wurde er zum Fellow of the Cambridge Philosophical Society ernannt. Drei Tage später erschien sein Name auf der Kandidatenliste für den Titel Fellow of the Royal Society (FRS). Er war von zahlreichen namhaften Mathematikern „für seine Untersuchung von elliptischen Funktionen und der Zahlentheorie“ vorgeschlagen worden. Unter anderem sprachen sich Hardy, Littlewood, Percy Alexander MacMahon, Joseph Larmor, Thomas John I’Anson Bromwich, Seth Barnes Nicholson, Alfred Young, Edmund Taylor Whittaker, Andrew Russell Forsyth und Alfred North Whitehead für ihn aus. Aber auch Hobson und Baker, die zwei Professoren, die Ramanujans Anfrage fünf Jahre zuvor unkommentiert zurückgeschickt hatten, befürworteten die Kandidatur. Die Auszeichnung erfolgte am 2. Mai. Ramanujan war damit erst der zweite Inder, dem diese Ehre zuteilwurde, und einer der jüngsten Fellows. Noch im selben Jahr, am 10. Oktober, erhielt er zusätzlich noch den Titel Fellow of Trinity College Cambridge.

Jahre nach Ramanujans Tod wurde Hardy von dem ungarischen Mathematiker Paul Erdős nach seinem größten Beitrag zur Mathematik gefragt. Ohne zu zögern, nannte Hardy die Entdeckung Ramanujans und bezeichnete sie als „den einzigen romantischen Vorfall in meinem Leben“.[34]

Krankheit, Rückkehr nach Indien und Tod

Ramanujan, Passfoto von 1919, angefertigt für seine Rückreise nach Indien. Das Foto ist geglättet.

Typische Dorfstraße im Vorort Chetput von Madras, um 1905

Ramanujan hatte zeitlebens gesundheitliche Probleme. In dieser Hinsicht tat ihm der Aufenthalt in England nicht gut, zumal er als Brahmane streng vegetarisch lebte, was seine Ernährung während des Ersten Weltkrieges zusätzlich erschwerte. Nachdem er zweimal an Bakterienruhr erkrankt war, wurden sowohl Tuberkulose als auch Vitaminmangel diagnostiziert. Ramanujans fatalistische Einstellung, die Hardy auf seine indische Herkunft zurückführte,[35] trug zusätzlich dazu bei, dass er zu wenig auf seine eigene Gesundheit achtete.

Das Jahr 1917 war für Ramanujan von Enttäuschungen geprägt. Zunächst wurde er nicht wie erhofft zum Fellow des Trinity College gewählt (das College war damals wegen der Affäre um den Kriegsgegner Bertrand Russell zerstritten).[36] Dann erkrankte er so schwer, dass er zeitweise um sein Leben fürchtete. Der Aufenthalt im Tuberkulose-Sanatorium in Matlock verschlechterte seine Stimmung zu einer tiefen Depression: Der Ort war abgelegen, die Leitung diktatorisch, die Patienten wurden von der Außenwelt isoliert, es war kalt (was man damals für therapeutisch sinnvoll hielt), und er bekam nicht das gewohnte Essen. Seine Arbeit litt unter der Erkrankung, was wiederum seine Depression verstärkte. Außerdem bekam er nur noch selten Briefe von seiner Frau; wie sich später herausstellte, wurden sie von seiner Mutter abgefangen.[37] Im Februar 1918 unternahm Ramanujan einen Suizidversuch, indem er sich vor einem einfahrenden U-Bahn-Zug auf die Schienen warf, doch ein aufmerksamer Wachtposten konnte den Zug noch rechtzeitig zum Stehen bringen. Ramanujan erlitt Verletzungen, die an seinem Schienbein tiefe Narben hinterließen. Er wurde festgenommen und kam nur dank Hardys Einschreiten frei.[38] Ende 1917 sah Hardy aber Anzeichen für eine Besserung und schrieb in einem Brief an Francis Dewsbury in Madras im Januar 1918, Ramanujan habe fast 15 Pfund zugenommen und seine Körpertemperatur sei stabil.[39]

Ramanujan beschloss, nach dem Ende des Krieges nach Indien zurückzureisen. Als Fellow der Royal Society bot man ihm in Madras eine Professur (Fellowship der Universität) an, die ihm mit 250 Pfund etwa das gleiche Gehalt bot wie als Fellow der Royal Society.[40] Ramanujan wollte aber erst gesund werden und spendete sogar Gelder aus seinem Einkommen bei der Royal Society, zum Unwillen seiner Familie, die auf seine Unterstützung angewiesen war.

Am 27. Februar 1919 brach Ramanujan von England auf, erreichte Indien am 13. März und wurde von seiner Mutter in Madras empfangen. Familienkonflikte brachen wieder auf, als Ramanujan darauf bestand, dass seine Frau Janaki, nunmehr 18 Jahre alt, zu ihm kam. Sein Wesen hatte sich verändert: statt herzlich und freundschaftlich wie vor seiner Abreise erschien er seinen Freunden nun depressiv, kalt und mürrisch, er war nicht mehr wohlgenährt wie vor seiner Abfahrt, sondern sah kränklich und abgemagert aus.[41] Es wurde erwogen, ihn in ein Sanatorium zu schicken, aber Ramanujan war misstrauisch gegen Ärzte geworden und verweigerte sich häufig ihrem Rat. Auf Hardys Drängen schickte man in Madras den Tuberkulosespezialisten und Professor P. S. Chandrasekhar zu Ramanujan, der eindeutig Tuberkulose diagnostizierte.[42]

Im Sommer zog die Familie vom heißen Madras ins kühlere Landesinnere, zunächst nach Kodumudi, wohin die Familie der Mutter gute Verbindungen hatte, ab Anfang September in das weniger abgelegene Kumbakonam. Anfang 1920 war Ramanujan wieder in Chetpet, einem Vorort von Madras, wo er noch einmal eine produktive Phase erlebte. Am 12. Januar 1920 schrieb er Hardy über die Entdeckung der Mock-Thetafunktionen. Bis vier Tage vor seinem Tod arbeitete er trotz Fiebers und Schmerzen an seinen mathematischen Notizbüchern, deren Blätter seine Frau in einer Schachtel sammelte.[43]

Ramanujan starb am 26. April 1920 in Chetpet im Haus Gometra außerhalb der Huntington Road.[44] Seine Witwe lebte bis zu ihrem Tod 1994 in Triplicane, einem Stadtteil von Madras, wo sie später ihren Unterhalt überwiegend als selbständige Schneiderin verdiente (und eine kleine Rente der Universität Madras erhielt) und einen angenommenen Sohn einer verstorbenen Freundin (W. Narayanan) großzog.[45]

Der Arzt D. A. B. Young untersuchte im Jahr 1994 Ramanujans Krankenakten und medizinische Unterlagen und äußerte die Vermutung, er sei nicht an Tuberkulose, sondern an Amöbenruhr gestorben, die damals in Madras grassierte. Zudem war er der Meinung, dass Ramanujans Bakterienruhr nicht vollständig abgeklungen sei und die Erreger im Körper verblieben waren. So konnte sich die Amöbenruhr später umso schneller entwickeln.

Das Werk

Ramanujan beschäftigte sich während der fünf Jahre in England hauptsächlich mit der Zahlentheorie. Dabei wurde er durch viele Summenformeln, die Konstanten wie die Kreiszahl $\pi ,$ Primzahlen und Partitionsfunktionen enthalten, berühmt und er war ein Meister im Umgang mit Kettenbrüchen. Unter anderem erstellte er eine sehr gute Näherungsformel für die Berechnung des Ellipsenumfangs.

Kreiszahlberechnung

Zu seinen bekanntesten Erkenntnissen zählt eine 1914 veröffentlichte, auf Untersuchungen von elliptischen Funktionen und Modulfunktionen basierende Gleichung zur Berechnung der Kreiszahl $\pi$ :[46][47]

{\frac {1}{\pi }}={\frac {2{\sqrt {2}}}{9801}}\cdot \sum _{n=0}^{\infty }\,{\frac {(4n)!\cdot (1103+26390\,n)}{(n!)^{4}\cdot 396^{4n}}}

Das Verfahren konvergiert schnell und liefert nach 9 Schritten über einen Näherungsbruch mit 80-stelligem Zähler bereits ein Resultat, das auf 70 Nachkommastellen[48][49] mit $\pi$ übereinstimmt:

{\begin{aligned}\pi &\approx {\frac {1}{{\frac {2{\sqrt {2}}}{9801}}\cdot \sum _{n=0}^{8}\,{\frac {(4n)!\cdot (1103+26390\,n)}{(n!)^{4}\cdot 396^{4n}}}}}={\sqrt {2}}\cdot {\frac {14071471712843535798792494970078253119671801362717159118900747103370578550063104}{6334387787708107824222495376281706107615730472323276284056009760393364218543125}}\\\\&\approx 3{,}14159\;26535\;89793\;23846\;26433\;83279\;50288\;41971\;69399\;37510\;58209\;74944\;59230\;78164\;{\color {red}10719\ldots }\\\pi &=3{,}14159\;26535\;89793\;23846\;26433\;83279\;50288\;41971\;69399\;37510\;58209\;74944\;59230\;78164\;{06286\ldots }\end{aligned}}

Im Jahr 1985 nutzte Bill Gosper diesen Ansatz, um $\pi$ auf 17 Millionen Stellen hinter dem Komma zu bestimmen.

Partitionsfunktion

Die im Jahr 1918 veröffentlichte asymptotische Formel von Hardy und Ramanujan für die Partitionsfunktion $p(n)$ gibt die Anzahl der Zerfällungen einer natürlichen Zahl $n$ an:[50]

p(n)\sim {\frac {1}{4n{\sqrt {3}}}}\exp \left({\pi {\sqrt {\frac {2n}{3}}}}\right)\quad {\text{für}}\quad n\rightarrow \infty

.

Für beispielsweise $n=1000$ ergibt sie einen um nur 1,4 % zu hohen Wert, der bei rund $2{,}44\cdot 10^{31}$ liegt. Hardy und Ramanujan fanden eine exakte Formel für die Partitionsfunktion, deren erstes Glied der obige asymptotische Wert ist. Das beeindruckte auch den englischen Spezialisten für Kombinatorik Percy Alexander MacMahon, der Tafeln für die Partitionsfunktion mit Hilfe einer Formel von Euler berechnet hatte – der Wert $p(200)$ , von MacMahon in mühseliger Handarbeit tabelliert, ergab sich aus Ramanujans Formel unmittelbar. Die Arbeit zur Partitionsfunktion war auch der Ursprung der Kreismethode, die später von Hardy und Littlewood zu einer zentralen Methode der analytischen Zahlentheorie gemacht wurde.

Weitere Erkenntnisse

Insgesamt fand Ramanujan in Cambridge etwa 3900 mathematische Resultate, in der Mehrzahl Identitätsgleichungen, von denen die meisten im Nachhinein bewiesen werden konnten.

In den Jahren der gemeinsamen Arbeit mit Hardy entstanden zahlreiche Werke über hochzusammengesetzte Zahlen, Mock-Thetafunktionen (Pseudo-Thetafunktionen) – die lange rätselhaft waren, deren Theorie aber um 2010 einen großen Aufschwung erhielt (Sander Zwegers, Kathrin Bringmann, Ken Ono) – und die nach ihm benannte Vermutung über die Ramanujansche tau-Funktion, die im Jahr 1974 von Pierre Deligne bewiesen wurde. Gemeinsam bewiesen sie den Satz von Hardy und Ramanujan. Dieser Satz liefert die bis heute genaueste Schätzung für die Anzahl unterschiedlicher Primfaktoren einer ganzen Zahl.

Um Beispiele für die Art von Ramanujans Resultaten zu geben, seien hier ein paar weitere Gleichungen aufgeführt, die Ramanujan fand:

{\sqrt {(n+a)^{2}+x\,a+x\,{\sqrt {(n+a)^{2}+(x+n)\,a+(x+n)\,{\sqrt {(n+a)^{2}+(x+2n)\,a+(x+2n)\,{\sqrt {\dots }}}}}}}}=x\,+\,n\,+\,a

[51]

{\frac {1}{\displaystyle 1+{\frac {e^{-2\pi }}{\displaystyle 1+{\frac {e^{-4\pi }}{\displaystyle 1+{\frac {e^{-6\pi }}{\ddots }}}}}}}}={\Biggl (}{\sqrt {\frac {5+{\sqrt {5}}}{2}}}-{\frac {{\sqrt {5}}+1}{2}}{\Biggr )}\cdot e^{2\pi /5}={\Bigl (}{\sqrt {2+\Phi }}-\Phi {\Bigr )}\cdot e^{2\pi /5}

[52] … mit dem goldenen Schnitt

\Phi

{\frac {1}{\displaystyle 1+{\frac {e^{-2\pi {\sqrt {5}}}}{\displaystyle 1+{\frac {e^{-4\pi {\sqrt {5}}}}{\displaystyle 1+{\frac {e^{-6\pi {\sqrt {5}}}}{\ddots }}}}}}}}={\Biggl (}{\frac {\sqrt {5}}{1+{\sqrt[{5}]{5^{\frac {3}{4}}({\frac {{\sqrt {5}}-1}{2}})^{\frac {5}{2}}-1}}}}-{\frac {{\sqrt {5}}+1}{2}}{\Biggr )}\cdot e^{2\pi /{\sqrt {5}}}

[52]

Die beiden untersten Gleichungen handeln von der Rogers-Ramanujan-Kettenbruchfunktion R(x).

Nach Ramanujan benannte Konzepte

Landau-Ramanujan-Konstante (zusätzlich nach Edmund Landau benannt)
Ramanujan-Soldner-Konstante (weiterentwickelte Theorie des deutschen Mathematikers Johann Georg von Soldner)
Ramanujan-Thetafunktion
Rogers-Ramanujan-Identitäten (gemeinsam mit dem britischen Mathematiker Leonard James Rogers entwickelt)
Rogers-Ramanujan-Kettenbruch
Ramanujan-Primzahl
Ramanujansumme
Ramanujan-Vermutung (über die Ramanujan-tau-Funktion)
das offene Problem von Brocard und Ramanujan
Ramanujan-Graph
Ramanujan-Nagell-Gleichung
Ramanujansche g-Funktion und G-Funktion

Magisches Quadrat

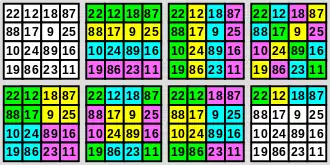
Das magische Quadrat von Ramanujan. Gleichfarbige Felder ergeben die Summe von 139, die erste Zeile – unten rechts farbig hervorgehoben – zeigt sein Geburtsdatum.

Ein ganzes Kapitel des ersten Notizbuchs ist magischen Quadraten gewidmet. Von ihm stammt das nebenstehende Quadrat, dessen erste Zeile sein Geburtsdatum zeigt.

Ramanujans Methoden und Bildungslücken

Nicht alle Resultate Ramanujans waren exakt. So gab er in einem seiner ersten Briefe eine Formel für die Anzahl der Primzahlen unterhalb einer festen Zahl $x$ in Form einer unendlichen Reihe an, die zwar für Werte bis etwa 1000 eine exakte Übereinstimmung ergibt (und auch für weit höhere Werte noch eine relativ gute Näherung liefert), aber, wie Littlewood fand, insgesamt nicht exakt ist.[53] Die Formel ähnelte der von Bernhard Riemann, wobei Ramanujans Formel die komplexen Nullstellen der Riemannschen Zetafunktionen nicht berücksichtigte.[54] Obwohl Ramanujan in der analytischen Zahlentheorie (und besonders der Primzahlverteilung) aufgrund seiner Kenntnismängel und der gerade hier – wo häufig scheinbar plausible Hypothesen sich im Nachhinein als falsch herausstellten[55] – wichtigen Notwendigkeit strenger Beweise zwangsläufig scheitern musste (Littlewood),[56] hielt Littlewood seine Beiträge dazu für eine seiner außerordentlichsten Leistungen.[57]

Hardy wurde oft gefragt,[58] ob Ramanujan ein spezielles Geheimnis oder „abnorme“ Methoden angewendet hätte, die ihn von anderen Mathematikern abhoben. Hardy erwiderte darauf, er könne das zwar nicht mit letzter Sicherheit beantworten, glaube es aber nicht.[59]

Ein Manko Ramanujans war, dass er nichts von der Theorie der Funktionen komplexer Variabler wusste (selbst seine Kenntnisse über elliptische Funktionen hatte er aus der eigenwilligen Darstellung des Lehrbuchs von Alfred George Greenhill),[60] wie Hardy noch in seinem Buch über Ramanujan konstatierte.[61] Später lernte er zwar etwas Funktionentheorie, benutzte aber zu Hardys Erstaunen nicht den Cauchyschen Integralsatz oder den Residuenkalkül, obwohl sie ihm als Formalisten hätten liegen müssen. Hardy charakterisierte Ramanujan als Meister im Umgang mit algebraischen Formeln und unendlichen Reihen, wie Hardy selbst es bei keinem ihm bekannten Mathematiker gesehen habe und was ihn nur mit Euler oder Jacobi vergleichbar mache.[58] Er arbeitete auch mehr als andere Mathematiker nach Hardy durch Induktion von numerischen Beispielen, zum Beispiel bei den von ihm entdeckten Kongruenzen der Partitionsfunktion. Nach Hardy vereinigte er ein außerordentliches Gedächtnis, Geduld und Ausdauer und außerordentliche rechnerische Fähigkeiten mit einer Fähigkeit zur Verallgemeinerung und zur raschen Änderung der von ihm aufgestellten Hypothesen sowie mit einem Gefühl für Form, die in Staunen versetzte und ihn auf seinem Gebiet zu seiner Zeit einzigartig machte.[62] Er sah es weniger als Tragödie an, dass Ramanujan früh verstarb (nach Hardy waren Mathematiker mit 30 Jahren sowieso schon relativ alt), als dass er in seinen frühen Jahren in Indien nicht gefördert wurde und so ein verzerrtes Bild der Mathematik erhalten hatte.[63] Nach Hardy wäre er trotz „profunder und unbezwingbarer Originalität“ ein größerer Mathematiker geworden, wäre er in seiner Jugend etwas „gezähmt“ worden,[64] dann aber „weniger ein Ramanujan als ein europäischer Professor geworden, und der Verlust wäre möglicherweise größer als der Gewinn gewesen“.[65]

Anekdoten

Eine Geschichte, die die rechnerischen Leistungen Ramanujans zum Ausdruck bringt, stammt von Hardy selbst, der sie nach Ramanujans Tod erzählte.[66][67] Hardy war mit einem Taxi mit der Nummer 1729 zu Ramanujan gefahren, hatte ein wenig über die Zahl nachgedacht, aber ohne etwas Besonderes zu finden, und teilte Ramanujan statt einer Begrüßung enttäuscht mit, was für eine uninteressante, nichtssagende Zahl das doch sei. Ramanujan, der krank im Bett lag, widersprach sogleich: 1729 sei sogar sehr interessant als die kleinste natürliche Zahl, die sich auf zwei unterschiedliche Weisen als Summe zweier Kubikzahlen darstellen lasse: $1729=1^{3}+12^{3}=9^{3}+10^{3}$ . Hardy fragte zurück, ob er auch die Antwort auf das entsprechende Problem für vierte Potenzen wisse. Nach kurzem Nachdenken meinte Ramanujan, ihm falle kein Beispiel ein, aber die erste derartige Zahl müsse sehr groß sein.[68]

Die Zahl 1729 wird mittlerweile auch als Hardy-Ramanujan-Zahl bezeichnet und ist die zweite Taxicab-Zahl. Die kleinste Lösung für die vierte Potenz ist $635\,318\,657=133^{4}+134^{4}=59^{4}+158^{4}$ .

J. E. Littlewood äußerte einmal, dass jede positive ganze Zahl Ramanujans persönlicher Freund sei.[57]

Eine weitere Geschichte hat Prasanta Chandra Mahalanobis überliefert, Ramanujans Freund aus Cambridge. Er stieß in Ramanujans Zimmer auf eine Denksportaufgabe des Strand Magazine vom Dezember 1914. Gegeben war eine Reihe von Häusern mit fortlaufenden Hausnummern 1, 2, 3 …. Gesucht war die Nummer desjenigen Hauses, bei dem die Summen aller Hausnummern rechts bzw. links davon gleich sind, wenn die Anzahl der Häuser größer als 50 und kleiner als 500 ist. Mahalanobis fand nach kurzem Nachdenken die Hausnummer 204 bei einer Gesamtzahl von 288 Häusern als einzige Lösung im gegebenen Intervall:

1+2+3+\cdots +203=20\,706=205+206+\cdots +288

Als er dann Ramanujan die Aufgabe vorlas, fand dieser nicht nur ebenso schnell diese spezielle Lösung, sondern formulierte dazu noch eine allgemeine Lösung für beliebig lange Straßen in Form eines Kettenbruchs.[69] Die möglichen Werte der Hausnummer sind die Wurzeln der Quadrat-Dreieckszahlen, der Index der Dreieckszahl ist dabei die Anzahl der Häuser. Unterhalb von 204 existieren noch die Lösungen 6 (bei 8 Häusern) und 35 (bei 49 Häusern).

Sonstige Interessen und Ansichten Ramanujans

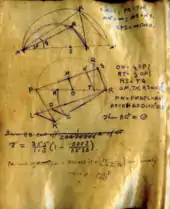
Manuskriptseite von Ramanujan zur Quadratur des Kreises (veröffentlicht 1913)

Laut Hardys Schilderungen interessierte sich Ramanujan nur geringfügig für Literatur und Kunst,[70] konnte aber gute von schlechter Literatur unterscheiden. Seine Englischkenntnisse waren so dürftig, dass er damit kein Examen hätte bestehen können;[71] mathematische Abhandlungen in deutscher oder französischer Sprache konnte er überhaupt nicht lesen. Er war sehr an Philosophie interessiert, politisch war er radikaler Pazifist. Er achtete zwar sehr auf die Einhaltung seiner religiösen Konventionen, war aber nicht ausschließlich von seiner Religion überzeugt, sondern der Ansicht, alle Religionen glichen einander mehr oder weniger. Er interessierte sich für Ungewöhnliches, Unerwartetes und Merkwürdiges und besaß eine kleine Sammlung von Büchern von Kreisquadrierern und anderen Cranks (Hardy). Ramanujan lieferte selbst zwei geometrische Konstruktionen zur genäherten Quadratur des Kreises.

Notizbücher

Ramanujans persönliche Aufzeichnungen, die „Notizbücher“, waren teilweise für einige Jahre verschollen. Seine Witwe übergab die vier Notizbücher und einige weitere Manuskripte[72] nach seinem Tod der University of Madras. Drei Jahre später sandte sie der dortige Registrar Francis Drewsbury an Godfrey Harold Hardy an die Universität von Cambridge. Das Original des ersten und zweiten Notizbuchs kehrte später wieder an die Universität Madras zurück.

Die vier Bücher und die Manuskripte enthielten insgesamt 3000 bis 4000 von Ramanujan[73] aufgestellte mathematische Formeln (im ersten Notizbuch 759 Resultate). Zu keiner jedoch war ein Beweis beigefügt.[74] Gemeinsam mit Bruce Berndt, einem Mathematiker von der University of Illinois at Urbana-Champaign, bewies George E. Andrews einen großen Teil der Formeln (unter Benutzung von Unterlagen von Bertram Martin Wilson und George Neville Watson und unter Beteiligung weiterer Mathematiker).

Ursprünglich war eine Veröffentlichung der Notizbücher schon mit den Collected Papers 1927 geplant, kam aber aus finanziellen Gründen nicht zustande. Im Jahr 1929 planten Wilson und Watson eine Herausgabe der Notizbücher, was aber durch Wilsons Tod 1935 zum Erliegen kam (1957 veröffentlichte das Tata Institute for Fundamental Research in Bombay eine photostatische Kopie in zwei Bänden, mit dem ersten, zweiten und dritten Notizbuch). Ende der 1930er Jahre verlor Watson das Interesse an der Herausgabe, seine Notizen und die von Wilson dienten aber später Berndt und Andrews bei deren Edition und Watson veröffentlichte über Material aus den Notizbüchern.[75] Die Notizbücher wurden später durch Andrews und Berndt herausgegeben.

Das zweite Notizbuch ist eine Erweiterung und Bearbeitung des ersten Notizbuchs und entstand vor Ramanujans Aufenthalt in England. Beide haben über 300 Seiten und sind zum großen Teil thematisch geordnet (im Zweiten Notizbuch 21 Kapitel von 256 Seiten und rund 100 Seiten nicht organisiertes Material). Rund 120 Ergebnisse teilte er Hardy brieflich mit (wobei vom ersten Brief eine Seite fehlt). Das dritte Notizbuch besteht aus nur 33 Seiten.

Das vierte Notizbuch entstand nach Ramanujans Rückkehr nach Indien und enthält unter anderem Material zu den Mock-Thetafunktionen, Rogers-Ramanujan-Kettenbrüchen und q-Reihen. Es war jahrzehntelang verschollen, was ihm den Beinamen „Verlorenes Notizbuch“ (Lost Notebook) einbrachte. Nach Watsons Tod im Jahre 1965 untersuchte Robert Alexander Rankin dessen Nachlass und schickte die dort noch vorhandenen Ramanujan’schen Schriften am 26. Dezember 1968 an die Wren Library des Trinity College. Dort wurde das Lost Notebook im Frühling des Jahres 1976 von Andrews aufgefunden, in einer Schachtel mit ehemals Watson gehörenden Gegenständen. Berndt äußerte sich darüber:

„Die Entdeckung dieses verlorenen Notizbuches verursachte ungefähr so viel Aufruhr in der mathematischen Welt, wie die Entdeckung von Beethovens zehnter Symphonie in der musischen Welt verursachen würde.“[76]

Am 22. Dezember 1987 (Ramanujans 100. Geburtstag) wurde Ramanujan’s Lost Notebook im mit dem Springer-Verlag vernetzten Narosa Publishing House veröffentlicht. Die ersten beiden Exemplare des Buches händigte der damalige indische Premierminister Rajiv Gandhi an S. Janaki Ammal Ramanujan, die Witwe des Mathematikers, und an George E. Andrews aus. Zu einigen Formeln konnten allerdings bis heute keine Beweise gefunden werden.

Ehrungen

Auszeichnungen zu seinen Lebzeiten

1904: K. Ranganatha Rao prize for mathematics
6. Dezember 1917: Mitglied der London Mathematical Society
18. Februar 1918: Fellow of the Cambridge Philosophical Society
2. Mai 1918: Fellow of the Royal Society
10. Oktober 1918: Fellow of Trinity College Cambridge

Postume Ehrungen

1962 gab die indische Regierung eine Briefmarke mit dem Konterfei Ramanujans heraus, um an seinen 75. Geburtstag zu erinnern. Heutzutage ziert der Mathematiker eine Reihe indischer Briefmarken.
Im indischen Bundesstaat Tamil Nadu, Ramanujans Heimatstaat, feiert man jedes Jahr am 22. Dezember, seinem Geburtstag, den State IT Day. Damit soll an die Wurzeln dieses Wissenschaftlers und seine Herkunft aus Tamil Nadu erinnert werden. Das Haus in der Saarangapani Street in Kumbakonam, in dem Ramanujan zusammen mit seiner Familie den größten Teil seiner Kindheit verbracht hat, beherbergt heute ein umfangreiches Museum über den Mathematiker.
Seit 2005 werden in Gedenken an Ramanujan der ICTP Ramanujan Prize sowie der SASTRA Ramanujan Prize verliehen.
2019 veröffentlichte ein Forscherteam um Gal Raayoni vom Technion einen Fachaufsatz über eine von ihnen entwickelte Software, die nach Ansicht ihrer Urheber die Arbeitsweise Ramanujans imitieren soll. Das Computerprogramm, genannt die „Ramanujan-Maschine“, soll nach dem Trial-and-Error-Verfahren bisher unbekannte verschachtelte Formeln gefunden haben, die den Wert wichtiger Konstanten wie Pi, der Eulerschen Zahl e oder Werte der riemannschen Zeta-Funktion ergeben.[77] Frank Calegari kritisierte die Behauptungen des Forscherteams als intellektuelle Hochstapelei.[78][79]
Der am 17. Februar 1988 entdeckte Asteroid (4130) Ramanujan wurde 1989 nach ihm benannt.[80]

Bezüge auf Ramanujan in der Kultur

Im Film Good Will Hunting wird Ramanujan von Mathematikprofessor Gerald Lambeau – etwas überdramatisiert[81] – als Vergleich für die Hochbegabung des jungen Will Hunting angeführt.
Die US-Krimiserie Numbers – Die Logik des Verbrechens übertrug Ramanujans Namen auf eine indischstämmige Mathematikerin, die sich auf Kombinatorik spezialisierte.[82]
Das Drama First Class Man, basierend auf dem gleichnamigen Roman von David Freeman, handelt von Ramanujan und seiner Arbeitsbeziehung zu Hardy.
Am 21. April 1998 wurde die Oper Ramanujan des deutsch-indischen Komponisten Sandeep Bhagwati über das Leben des Mathematikers im Münchner Prinzregententheater uraufgeführt.[83]
2014 erschien der biographische Film Ramanujan.[84]
2016 erschien der Spielfilm Die Poesie des Unendlichen (englisch: The Man Who Knew Infinity) des Regisseurs Matthew Brown mit dem englischen Schauspieler Dev Patel in der Rolle von Srinivasa Ramanujan und Jeremy Irons als G. H. Hardy.

Schriften

Mit G. H. Hardy: Une formule asymptotique pour le nombre des partitions de n. Comptes Rendus 164, 1917, S. 35–38.
G. H. Hardy, P. Veṅkatesvara Seshu Aiyar, Bertram Martin Wilson (Hrsg.): Collected papers. Cambridge University Press, 1927; Reprint Chelsea Publishing Co. 1962; AMS Chelsea Publishing (Band 159) 2000, ISBN 0-8218-2076-1 (mit modernen Kommentaren von Bruce C. Berndt).
George E. Andrews, Bruce C. Berndt (Hrsg.): Ramanujan’s Lost Notebook. Springer-Verlag, New York London 2005, ISBN 978-0-387-25529-3.
Bruce C. Berndt (Hrsg.): Ramanujan’s Notebooks. (Fünf Teile), Springer-Verlag, New York.
- Part I, 1985, ISBN 0-387-96110-0.
- Part II, 1999, ISBN 0-387-96794-X.
- Part III, 2004, ISBN 0-387-97503-9.
- Part IV, 1993, ISBN 0-387-94109-6.
- Part V, 2005, ISBN 0-387-94941-0.
George E. Andrews, Robert Alexander Rankin (Hrsg.): Ramanujan – Letters and Commentary. American Mathematical Society, 1995, ISBN 978-0-8218-0470-4.
Ramanujan: The lost notebook and other unpublished papers. Narosa Publ. House/Springer, New Delhi 1988.

Literatur

Godfrey Harold Hardy: Obituary, S. Ramanujan. Nature, Band 105, 1920, S. 494–495.
Godfrey Harold Hardy: Ramanujan – Twelve Lectures on the Subjects Suggested by His Life and Work. Chelsea Publishing Co, 1940, 1978 ISBN 0-8284-0136-5.
Godfrey Harold Hardy: Srinivasan Ramanujan (1887–1920), Proc. London Math. Soc., Band 19, 1920, S. XL–LVIII, wieder abgedruckt in Hardy u. a. Ramanujan. Collected Papers, Cambridge UP, 1927, S. XXI–XXXVI (mit kleineren Änderungen auch in den Proc. Roy. Soc., 1921)
Robert Kanigel: Der das Unendliche kannte. Vieweg-Verlag, 2. Auflage 1995, ISBN 3-528-16509-X, deutsche Übersetzung durch Albrecht Beutelspacher von The Man Who Knew Infinity: a Life of the Genius Ramanujan. Charles Scribner’s Sons, New York 1991. ISBN 0-684-19259-4.
Eric Harold Neville: Srinivasa Ramanujan. Nature, Band 149, 1942, S. 292–295
S. R. Ranganathan: Ramanujan: the Man and the Mathematician, Bombay: Asia Publishing House 1967
Suresh Ram: Srinivasa Ramanujan, New Delhi, National Book Trust, 1972, 1979.
K. Srinivasa Rao: Srinivasa Ramanujan – A Mathematical Genius. East West Books, Madras 1998.
George E. Andrews (Hrsg.): Ramanujan revisited. (Urbana-Champaign, Ill., 1987), Academic Press 1988
George E. Andrews, Robert Alexander Rankin: Ramanujan: Essays and Surveys. American Mathematical Society, 2001, ISBN 978-0-8218-2624-9.
Bruce C. Berndt: An Overview of Ramanujan’s Notebooks. In: Charlemagne and His Heritage: 1200 Years of Civilization and Science in Europe. (Hrsg. P. L. Butzer, W. Oberschelp, H. Th. Jongen), Turnhout, 1998. S. 119–146.
Bruce C. Berndt, S. Bhargava: Ramanujan for lowbrows. In: American Mathematical Monthly. Band 100, 1993, S. 644 (mathdl.maa.org).
Robert Alexander Rankin: Ramanujan’s Manuscripts and Notebooks, Bulletin London Math. Soc., Band 14, 1982, S. 81–97, Teil 2, Band 21, 1989, S. 351–365
Lokenath Debnath: Srinivasa Ramanujan (1887-1920) and the theory of partitions of numbers and statistical mechanics. A centennial tribute, International Journal of Mathematics and Mathematical Sciences, Band 10, 1987, Heft 4, S. 625–640, European Digital Mathematics Library
Don Zagier: Ramanujan an Hardy. Vom ersten bis zum letzten Brief. In: Mitteilungen DMV. Band 18, 2010, S. 21–28 (people.mpim-bonn.mpg.de PDF).

Weblinks

Commons: Srinivasa Ramanujan – Sammlung von Bildern, Videos und Audiodateien

Wikiquote: S. Ramanujan – Zitate

John J. O’Connor, Edmund F. Robertson: Srinivasa Aiyangar Ramanujan. In: MacTutor History of Mathematics archive.
Website on Srinivasa Ramanujan – von Prof. K. Srinivasa Rao, Chennai, mit zahlreichen Scans der Artikel und Notizbücher, Juni 2002 (englisch)
Alladi Krishnaswami (Hrsg.): Srinivasa Ramanujan: Going Strong at 125, Part I. Notices AMS, Dezember 2012 und Teil 2. Notices AMS, Januar 2013
K. Srinivasa Rao: Srinivasa Ramanujan
Ein Genie mit Intuition: Ramanujan. (PDF; 685 kB) Kurzbiographie, Quarks & Co, 5. April 2005
Holger Dambeck: Mathematiker verneigen sich vor Ramanujan. In: Spiegel online. 22. Dezember 2012 (spiegel.de).
Martin Koch: Zu früh verstarb das vielleicht größte Mathe-Genie. Kannte Ramanujan das Unendliche? In: Berliner Zeitung. 29. April 1995 (berliner-zeitung.de).

Einzelnachweise und Anmerkungen

Robert Kanigel, übersetzt von Albrecht Beutelspacher: Der das Unendliche kannte; Das Leben des genialen Mathematikers Srinivasa Ramanujan, Springer-Verlag, 8. März 2013, S. 8–9 (eingeschränkte Vorschau in der Google-Buchsuche), abgerufen am 26. April 2020
Nach Robert Kanigel: Der das Unendliche kannte. Vieweg, 1995, S. 10, war Iyengar der Name einer Kaste, die ein Zweig der südindischen Brahmanen war.
Robert Kanigel: Der das Unendliche kannte. Vieweg 1995, S. 10
Robert Kanigel: Der das Unendliche kannte. 1995, S. 11
Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 24
imsc.res.in, abgerufen am 28. März 2020
imsc.res.in, abgerufen am 28. März 2020
Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 69
Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 77
P. V. Seshu Iyer: The Late Mr. S. Ramanujan, B.A., F.R.S. Juni 1920. In: Journal of the Indian Mathematical Society 12 (3). 83. Zitiert nach Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 81
Der Brief ist abgedruckt in Hardy u. a. (Hrsg.), Ramanujan, Collected Papers, Cambridge UP 1927, S. XXIII–XXVII.
Robert Kanigel: Der das Unendliche kannte. Vieweg 1995, S. 141, 142
Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 146
Hardy schildert seine Reaktion auf den Brief in: Hardy, Ramanujan, Cambridge UP 1940, S. 8–9
Hardy, Ramanujan, 1940, S. 9
Hardy: „The series formulae … I found much more intriguing, and it soon became obvious that Ramanujan must posess much more general theorems and was keeping a great deal up his sleave.“ In Hardy: Ramanujan. 1940, S. 9.
Nach Hardy, Ramanujan, 1940, S. 9. Gemeint ist Bailey: Generalized Hypergeometric Series, Cambridge UP 1932
Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 148
Dougall-Ramanujan-Identity, Mathworld
Hardy: „I had never seen anything in the least like them before. A single look at them is enough to show that they could only been written down by a mathematician of the highest class. They must be true because, if they were not true, no one would have had the imagination to invent them. Finally (you must remember that I knew nothing whatever about Ramanujan, and had to think of every possibility), the writer must be completely honest, because great mathematicians are commoner than thieves or humbugs of such incredible skill.“ In Hardy: Ramanujan. 1940, S. 9.
Hardy: Obituary, S. Ramanujan, Nature, Band 105, 1920, S. 494–495.
Eric Harold Neville: Srinivasa Ramanujan, Nature, Band 149, 1942, S. 292–295.
Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 153
Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 156
Robert Kanigel: Der das Unendliche kannte. 1995, S. 115
Robert Kanigel: Der das Unendliche kannte. 1995, S. 180
Hardys Räume lagen im New Court direkt neben (vom Innern des New Court aus rechts) dem Westportal, das zu einer Allee (Avenue) über den River Cam führte, im Aufgang A im zweiten Stock. Das Bishop’s Hostel, in dem Ramanujan wohnte, lag direkt östlich am New Court. Ramanujans erste Wohnung am Whewells Court lag östlich direkt gegenüber dem nordöstlich vom New Court gelegenen Great Court des Trinity College, auf der anderen Seite der Trinity Street. Siehe Karte in Robert Kanigel: Der das Unendliche kannte. 1995, Vorsatzseiten und S. 179 (zu Hardys Räumen)
Robert Kanigel: Der das Unendliche kannte. 1995, S. 179
„I can believe that he is at least a Jacobi.“ Brief an Hardy 1913.
Godfrey Harold Hardy: Collected Papers of G. H. Hardy. Cambridge UP 1927, S. XXXV.
Robert Kanigel: Der das Unendliche kannte. Vieweg 1995, S. 226
Biographie der University of St Andrews, Scotland, abgerufen am 4. April 2020
Ramanujan: On highly composite numbers. Proc. London Math. Soc., Series 2, Band 14, 1915, S. 347–400. Aus finanziellen Gründen konnte Ramanujans Aufsatz damals nicht vollständig veröffentlicht werden, das unveröffentlichte Material erschien viele Jahre später in Ramanujan: The lost notebook and other unpublished papers. Narosa Publ. House, Springer, New Delhi 1988 und in Jean-Louis Nicholas, Guy Robin (Herausgeber und Anmerkungen), Ramanujan: Highly composite numbers. Ramanujan Journal, Band 1, 1997, S. 119–153, PDF.
„I owe more to him as to anyone else in the world with one exception, and my association with him is the one romantic incident in my life.“ In Hardy: Ramanujan. Cambridge University Press, 1940, S. 2.
„Like all Indians he is fatalistic, and it is terribly hard to get him to take care of himself.“ Zitiert in mathshistory.st-andrews.ac.uk. Aufgerufen am 4. April 2020.
Kanigel, Der das Unendlich kannte, Vieweg 1995, S. 257 f.
Robert Kanigel: Der das Unendliche kannte. Vieweg 1995, S. 241
Robert Kanigel: Der das Unendliche kannte. Vieweg 1995, S. 261. Die Angaben über den Suizid Ramanujans und das Datum stammen aus den Aufzeichnungen von S. Chandrasekhar. Andere geben die zweite Jahreshälfte 1917 für den Suizidversuch an. Kanigel, S. 336
Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 274, Anmerkung dazu S. 336
Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 277.
Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 282.
Robert Kanigel: Der das Unendliche kannte. 1995, S. 285.
Robert Kanigel: Der das Unendliche kannte. 1995, S. 292.
Robert Kanigel: Der das Unendliche kannte. 1995, S. 292
Ramanujan´s wife Janakiammal (Janaki). PDF.
S. Ramanujan: Modular equations and approximations to $\pi$ . Quarterly Journal of Mathematics, Band 45, 1914, S. 350–372, abgerufen am 18. April 2020.
Jonathan Borwein, Peter Borwein, D. H. Bailey, Ramanujan: Modular equations and approximations to pi or how to compute one billion digits of pi. (PDF) American Mathematical Monthly, Band 96, 1989, S. 201–219, abgerufen am 18. April 2020.
Berechnung bei Wolfram Alpha ergibt eine Differenz in der Größenordnung 10⁻⁷².
Ergebnis der Berechnung $\pi \approx \ldots$ auf wolframalpha.com. wähle → „More digits“
Hardy, Ramanujan: Asymptotic Formulae in Combinatory Analysis. Proc. London Math. Soc., Band 17, 1918, S. 75–115, (ramanujan.sirinudi.org PDF).
Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 77
Eric W. Weisstein: Ramanujan Continued Fractions. In: MathWorld (englisch).
Kanigel: The man who knew infinity. S. 218.
Brief von Hardy an Ramanujan vom 26. März 1913. Nach Bruce Berndt, Robert Rankin: Ramanujan, Letters and Commentary. AMS S. 77.
„The analytical theory of numbers is one of those exceptional branches of mathematics in which proof really is everything and nothing short of absolute rigor counts.“ In Hardy: Ramanujan. 1940, S. 19.
Littlewood: A mathematician’s miscellany. Methuen 1953, S. 87, Besprechung der Collected Papers von Ramanujan.
Hardy, in: Collected Papers of Srinivasa Ramanujan. Cambridge University Press, 1927, S. XXXV.
Hardy in: Ramanujan, Collected Papers. 1927, S. XXXV.
Hardy: “My belief is that all mathematicians think, at bottom, in the same kind of way, and that Ramanujan was no exception.”
Littlewood: A mathematician’s miscellany. Hardy schrieb dagegen (Ramanujan, 1940, S. 10), er wüsste nicht genau, woher Ramanujans Kenntnisse auf diesem Gebiet stammen und ob er Greenhill oder Cayley gelesen hätte und bedauerte, Ramanujan damals nicht gefragt zu haben.
“Analysis proper Ramanujan’s work is less impressive, since he knew no theory of functions, and you cannot do real analysis without it.” In Hardy: Ramanujan. 1940, S. 14.
“He was by far the greatest formalist of his time,” auch wenn die „große Zeit der Formeln“ in der Mathematik schon rund 100 Jahre vorbei wäre. In Hardy: Ramanujan, Collected Papers. 1927, S. XXXV. Nochmals zitiert und von Hardy bestätigt in Hardy: Ramanujan. 1940, S. 14.
„… during his five unfortunate years, his genius was misdirected, sidetracked and to an certain extent distorted.“ In Hardy: Ramanujan. 1940, S. 6.
Hardy in: Ramanujan, Collected Papers. 1927, S. XXXVI.
Diesen Zusatz aus seinem Vorwort zu Ramanjans Collected Papers tat Hardy später in seinem Buch Ramanujan von 1940, S. 7, allerdings als lächerliche Sentimentalität seinerseits ab.
The Hardy-Ramanujan Number. (Memento vom 28. Mai 2013 im Internet Archive).
Hardy in Hardy u. a. (Hrsg.), Ramanujan, Collected Works, 1927, S. XXXV, nochmals von Hardy zitiert in Hardy, Ramanujan 1940, S. 12
Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 276.
Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 191.
Hardy in: Ramanujan, Collected Papers. 1927, S. XXXI, zu seinen außermathematischen Interessen.
Hardy in: Collected Papers. S. XXV.
Srinivasa Ramanujan: Manuscript Book 1 of Srinivasa Ramanujan. (PDF) School of Mathematics, abgerufen am 11. April 2020.
Schätzung von Hardy, durch Berndt bestätigt. Berndt: An overview of Ramanjuans notebooks. PDF. Danach gab es 3254 Resultate in den Notizbüchern, mit Interpretationsspielraum bei der Zählung. Nach Berndt war mindestens die Hälfte der Resultate neu (nicht nur ein Drittel, wie Hardy schätzte).
abgesehen von etwa 10 bis 20 Resultaten, die eine Beweisskizze enthielten (Berndt), manchmal nur aus einem Satz bestehend.
Die Geschichte der Notizbücher ist im Vorwort der Ausgabe von Berndt und Andrews dargestellt. Siehe auch Berndt: An overview of Ramanjuans notebooks. PDF.
„Raiders of the Lost Notebook“. Englischer Text über den Versuch, die Formeln der Notizbücher zu beweisen.
»Ramanujan-Maschine«: Computer mit legendärer Mathe-Intuition. Spektrum 10. Juli 2019.
Frank Calegari, The Ramanujan machine as intellectual fraud, Blog von Calegari, 17. Juli 2019, abgerufen 1. August 2019
Eduard Kaeser: Künstliche Intelligenz soll auch kreativ werden. NZZ, 2021-02-10, abgerufen am 16. Februar 2021.
Minor Planet Circ. 15261.
Lambeau stellt R. als einfachen Mann ohne Schulbildung dar, der erst im Erwachsenenalter auf ein altes Mathematikbuch stieß
Amita Ramanujan in der US-TV-Serie Numb3rs.
Ulrich Möller-Arnsberg: Die Münchner Biennale 1998. Das Eigene im Fremden – das Fremde im Eigenen. (Nicht mehr online verfügbar.) In: GEMA-Nachrichten 157. Juni 1998, archiviert vom Original am 7. Januar 2002; abgerufen am 2. Dezember 2010.
Ramanujan in der Internet Movie Database (englisch)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Robert Kanigel, übersetzt von Albrecht Beutelspacher: Der das Unendliche kannte; Das Leben des genialen Mathematikers Srinivasa Ramanujan, Springer-Verlag, 8. März 2013, S. 8–9 (eingeschränkte Vorschau in der Google-Buchsuche), abgerufen am 26. April 2020

[2] Nach Robert Kanigel: Der das Unendliche kannte. Vieweg, 1995, S. 10, war Iyengar der Name einer Kaste, die ein Zweig der südindischen Brahmanen war.

[3] Robert Kanigel: Der das Unendliche kannte. Vieweg 1995, S. 10

[4] Robert Kanigel: Der das Unendliche kannte. 1995, S. 11

[5] Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 24

[6] sc.res.in, abgerufen am 28. März 2020

[7] sc.res.in, abgerufen am 28. März 2020

[8] Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 69

[9] Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 77

[10] P. V. Seshu Iyer: The Late Mr. S. Ramanujan, B.A., F.R.S. Juni 1920. In: Journal of the Indian Mathematical Society 12 (3). 83. Zitiert nach Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 81

[11] Der Brief ist abgedruckt in Hardy u. a. (Hrsg.), Ramanujan, Collected Papers, Cambridge UP 1927, S. XXIII–XXVII.

[12] Robert Kanigel: Der das Unendliche kannte. Vieweg 1995, S. 141, 142

[13] Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 146

[14] Hardy schildert seine Reaktion auf den Brief in: Hardy, Ramanujan, Cambridge UP 1940, S. 8–9

[15] Hardy, Ramanujan, 1940, S. 9

[16] Hardy: „The series formulae … I found much more intriguing, and it soon became obvious that Ramanujan must posess much more general theorems and was keeping a great deal up his sleave.“ In Hardy: Ramanujan. 1940, S. 9.

[17] Nach Hardy, Ramanujan, 1940, S. 9. Gemeint ist Bailey: Generalized Hypergeometric Series, Cambridge UP 1932

[18] Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 148

[19] Dougall-Ramanujan-Identity, Mathworld

[20] Hardy: „I had never seen anything in the least like them before. A single look at them is enough to show that they could only been written down by a mathematician of the highest class. They must be true because, if they were not true, no one would have had the imagination to invent them. Finally (you must remember that I knew nothing whatever about Ramanujan, and had to think of every possibility), the writer must be completely honest, because great mathematicians are commoner than thieves or humbugs of such incredible skill.“ In Hardy: Ramanujan. 1940, S. 9.

[Hardy_a-21] Hardy: Obituary, S. Ramanujan, Nature, Band 105, 1920, S. 494–495.

[Neville_a-22] Eric Harold Neville: Srinivasa Ramanujan, Nature, Band 149, 1942, S. 292–295.

[23] Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 153

[24] Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 156

[25] Robert Kanigel: Der das Unendliche kannte. 1995, S. 115

[26] Robert Kanigel: Der das Unendliche kannte. 1995, S. 180

[27] Hardys Räume lagen im New Court direkt neben (vom Innern des New Court aus rechts) dem Westportal, das zu einer Allee (Avenue) über den River Cam führte, im Aufgang A im zweiten Stock. Das Bishop’s Hostel, in dem Ramanujan wohnte, lag direkt östlich am New Court. Ramanujans erste Wohnung am Whewells Court lag östlich direkt gegenüber dem nordöstlich vom New Court gelegenen Great Court des Trinity College, auf der anderen Seite der Trinity Street. Siehe Karte in Robert Kanigel: Der das Unendliche kannte. 1995, Vorsatzseiten und S. 179 (zu Hardys Räumen)

[28] Robert Kanigel: Der das Unendliche kannte. 1995, S. 179

[29] „I can believe that he is at least a Jacobi.“ Brief an Hardy 1913.

[30] Godfrey Harold Hardy: Collected Papers of G. H. Hardy. Cambridge UP 1927, S. XXXV.

[31] Robert Kanigel: Der das Unendliche kannte. Vieweg 1995, S. 226

[32] Biographie der University of St Andrews, Scotland, abgerufen am 4. April 2020

[33] Ramanujan: On highly composite numbers. Proc. London Math. Soc., Series 2, Band 14, 1915, S. 347–400. Aus finanziellen Gründen konnte Ramanujans Aufsatz damals nicht vollständig veröffentlicht werden, das unveröffentlichte Material erschien viele Jahre später in Ramanujan: The lost notebook and other unpublished papers. Narosa Publ. House, Springer, New Delhi 1988 und in Jean-Louis Nicholas, Guy Robin (Herausgeber und Anmerkungen), Ramanujan: Highly composite numbers. Ramanujan Journal, Band 1, 1997, S. 119–153, PDF.

[34] „I owe more to him as to anyone else in the world with one exception, and my association with him is the one romantic incident in my life.“ In Hardy: Ramanujan. Cambridge University Press, 1940, S. 2.

[35] „Like all Indians he is fatalistic, and it is terribly hard to get him to take care of himself.“ Zitiert in mathshistory.st-andrews.ac.uk. Aufgerufen am 4. April 2020.

[36] Kanigel, Der das Unendlich kannte, Vieweg 1995, S. 257 f.

[37] Robert Kanigel: Der das Unendliche kannte. Vieweg 1995, S. 241

[38] Robert Kanigel: Der das Unendliche kannte. Vieweg 1995, S. 261. Die Angaben über den Suizid Ramanujans und das Datum stammen aus den Aufzeichnungen von S. Chandrasekhar. Andere geben die zweite Jahreshälfte 1917 für den Suizidversuch an. Kanigel, S. 336

[39] Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 274, Anmerkung dazu S. 336

[40] Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 277.

[41] Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 282.

[42] Robert Kanigel: Der das Unendliche kannte. 1995, S. 285.

[43] Robert Kanigel: Der das Unendliche kannte. 1995, S. 292.

[44] Robert Kanigel: Der das Unendliche kannte. 1995, S. 292

[45] Ramanujan´s wife Janakiammal (Janaki). PDF.

[46] S. Ramanujan: Modular equations and approximations to $\pi$ . Quarterly Journal of Mathematics, Band 45, 1914, S. 350–372, abgerufen am 18. April 2020.

[47] Jonathan Borwein, Peter Borwein, D. H. Bailey, Ramanujan: Modular equations and approximations to pi or how to compute one billion digits of pi. (PDF) American Mathematical Monthly, Band 96, 1989, S. 201–219, abgerufen am 18. April 2020.

[48] Berechnung bei Wolfram Alpha ergibt eine Differenz in der Größenordnung 10⁻⁷².

[49] Ergebnis der Berechnung $\pi \approx \ldots$ auf wolframalpha.com. wähle → „More digits“

[50] Hardy, Ramanujan: Asymptotic Formulae in Combinatory Analysis. Proc. London Math. Soc., Band 17, 1918, S. 75–115, (ramanujan.sirinudi.org PDF).

[51] Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 77

[RaCoFra-52] Eric W. Weisstein: Ramanujan Continued Fractions. In: MathWorld (englisch).

[53] Kanigel: The man who knew infinity. S. 218.

[54] Brief von Hardy an Ramanujan vom 26. März 1913. Nach Bruce Berndt, Robert Rankin: Ramanujan, Letters and Commentary. AMS S. 77.

[55] „The analytical theory of numbers is one of those exceptional branches of mathematics in which proof really is everything and nothing short of absolute rigor counts.“ In Hardy: Ramanujan. 1940, S. 19.

[56] Littlewood: A mathematician’s miscellany. Methuen 1953, S. 87, Besprechung der Collected Papers von Ramanujan.

[hardy-xxxv-57] Hardy, in: Collected Papers of Srinivasa Ramanujan. Cambridge University Press, 1927, S. XXXV.

[auto-58] Hardy in: Ramanujan, Collected Papers. 1927, S. XXXV.

[59] Hardy: “My belief is that all mathematicians think, at bottom, in the same kind of way, and that Ramanujan was no exception.”

[60] Littlewood: A mathematician’s miscellany. Hardy schrieb dagegen (Ramanujan, 1940, S. 10), er wüsste nicht genau, woher Ramanujans Kenntnisse auf diesem Gebiet stammen und ob er Greenhill oder Cayley gelesen hätte und bedauerte, Ramanujan damals nicht gefragt zu haben.

[61] “Analysis proper Ramanujan’s work is less impressive, since he knew no theory of functions, and you cannot do real analysis without it.” In Hardy: Ramanujan. 1940, S. 14.

[62] “He was by far the greatest formalist of his time,” auch wenn die „große Zeit der Formeln“ in der Mathematik schon rund 100 Jahre vorbei wäre. In Hardy: Ramanujan, Collected Papers. 1927, S. XXXV. Nochmals zitiert und von Hardy bestätigt in Hardy: Ramanujan. 1940, S. 14.

[63] „… during his five unfortunate years, his genius was misdirected, sidetracked and to an certain extent distorted.“ In Hardy: Ramanujan. 1940, S. 6.

[64] Hardy in: Ramanujan, Collected Papers. 1927, S. XXXVI.

[65] Diesen Zusatz aus seinem Vorwort zu Ramanjans Collected Papers tat Hardy später in seinem Buch Ramanujan von 1940, S. 7, allerdings als lächerliche Sentimentalität seinerseits ab.

[66] The Hardy-Ramanujan Number. (Memento vom 28. Mai 2013 im Internet Archive).

[67] Hardy in Hardy u. a. (Hrsg.), Ramanujan, Collected Works, 1927, S. XXXV, nochmals von Hardy zitiert in Hardy, Ramanujan 1940, S. 12

[68] Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 276.

[69] Robert Kanigel: Der das Unendliche kannte. 2. Auflage, Vieweg, 1995, S. 191.

[70] Hardy in: Ramanujan, Collected Papers. 1927, S. XXXI, zu seinen außermathematischen Interessen.

[71] Hardy in: Collected Papers. S. XXV.

[72] Srinivasa Ramanujan: Manuscript Book 1 of Srinivasa Ramanujan. (PDF) School of Mathematics, abgerufen am 11. April 2020.

[73] Schätzung von Hardy, durch Berndt bestätigt. Berndt: An overview of Ramanjuans notebooks. PDF. Danach gab es 3254 Resultate in den Notizbüchern, mit Interpretationsspielraum bei der Zählung. Nach Berndt war mindestens die Hälfte der Resultate neu (nicht nur ein Drittel, wie Hardy schätzte).

[74] sehen von etwa 10 bis 20 Resultaten, die eine Beweisskizze enthielten (Berndt), manchmal nur aus einem Satz bestehend.

[75] Die Geschichte der Notizbücher ist im Vorwort der Ausgabe von Berndt und Andrews dargestellt. Siehe auch Berndt: An overview of Ramanjuans notebooks. PDF.

[76] „Raiders of the Lost Notebook“. Englischer Text über den Versuch, die Formeln der Notizbücher zu beweisen.

[77] »Ramanujan-Maschine«: Computer mit legendärer Mathe-Intuition. Spektrum 10. Juli 2019.

[78] Frank Calegari, The Ramanujan machine as intellectual fraud, Blog von Calegari, 17. Juli 2019, abgerufen 1. August 2019

[79] Eduard Kaeser: Künstliche Intelligenz soll auch kreativ werden. NZZ, 2021-02-10, abgerufen am 16. Februar 2021.

[80] Minor Planet Circ. 15261.

[81] Lambeau stellt R. als einfachen Mann ohne Schulbildung dar, der erst im Erwachsenenalter auf ein altes Mathematikbuch stieß

[82] Amita Ramanujan in der US-TV-Serie Numb3rs.

[83] Ulrich Möller-Arnsberg: Die Münchner Biennale 1998. Das Eigene im Fremden – das Fremde im Eigenen. (Nicht mehr online verfügbar.) In: GEMA-Nachrichten 157. Juni 1998, archiviert vom Original am 7. Januar 2002; abgerufen am 2. Dezember 2010.

[84] Ramanujan in der Internet Movie Database (englisch)