Raytracing
Raytracing (dt. Strahlverfolgung[1] oder Strahlenverfolgung,[2] in englischer Schreibweise meist ray tracing) ist ein auf der Aussendung von Strahlen basierender Algorithmus zur Verdeckungsberechnung, also zur Ermittlung der Sichtbarkeit von dreidimensionalen Objekten von einem bestimmten Punkt im Raum aus. Ebenfalls mit Raytracing bezeichnet man mehrere Erweiterungen dieses grundlegenden Verfahrens, die den weiteren Weg von Strahlen nach dem Auftreffen auf Oberflächen berechnen.
Prominenteste Verwendung findet Raytracing in der 3D-Computergrafik. Hier ist der grundlegende Raytracing-Algorithmus eine Möglichkeit zur Darstellung einer 3D-Szene. Erweiterungen, die den Weg von Lichtstrahlen durch die Szene simulieren, dienen, ebenso wie das Radiosity-Verfahren, der Berechnung der Lichtverteilung.
Weitere Anwendungsgebiete von Raytracing sind die Auralisation und Hochfrequenztechnik.
Ursprung und Bedeutung

Vor der Entwicklung von Raytracing bestand das junge Gebiet der 3D-Computergrafik im Wesentlichen aus einer Reihe von „Programmiertricks“, mit denen die Schattierung von beleuchteten Objekten nachgeahmt werden sollte. Raytracing war der erste Algorithmus auf diesem Gebiet, der einen gewissen physikalischen Sinn ergab.
Das erste mit Raytracing berechnete Bild wurde 1963 an der University of Maryland auf einem oszilloskopartigen Bildschirm ausgegeben.[3] Als Entwickler des Raytracing-Algorithmus gelten oft Arthur Appel, Robert Goldstein und Roger Nagel, die den Algorithmus Ende der 1960er Jahre veröffentlichten.[4][5][6] Weitere Forscher, die sich zu dieser Zeit mit Raytracing-Techniken beschäftigten, waren Herb Steinberg, Marty Cohen und Eugene Troubetskoy.[7] Raytracing basiert auf der geometrischen Optik, bei der das Licht als eine Gruppe von Strahlen verstanden wird. Die beim Raytracing verwendeten Techniken wurden bereits wesentlich früher, unter anderem von Herstellern optischer Systeme, verwendet. Heute verwenden viele Renderer (Computerprogramme zur Erzeugung von Bildern aus einer 3D-Szene) Raytracing, eventuell in Kombination mit weiteren Verfahren.
Einfache Formen des Raytracings berechnen nur die direkte Beleuchtung, also das direkt von den Lichtquellen eintreffende Licht. Raytracing wurde seit seiner ersten Verwendung in der Computergrafik jedoch mehrmals wesentlich erweitert. Weiterentwickelte Formen berücksichtigen auch das indirekte Licht, das von anderen Objekten reflektiert wird; man spricht dann von einem globalen Beleuchtungsverfahren.
Der Begriff Raycasting bezeichnet meist eine vereinfachte Form des Raytracings, wird teilweise aber auch synonym dazu gebraucht.
Grundprinzip
Die Erzeugung eines Rasterbildes aus einer 3D-Szene wird Rendern oder Bildsynthese genannt. Voraus geht die Erstellung einer solchen Szene vom Benutzer mit Hilfe eines 3D-Modellierungswerkzeugs.
In der Szenenbeschreibung werden zumindest folgende Daten angegeben:
- die Position der elementaren Primitive, wie Polygone oder Kugeln, aus denen sich die Objekte der Szene zusammensetzen;
- die lokalen Beleuchtungsmodelle und deren Parameter, die die Farben und Materialien der einzelnen Objekte der Szene bestimmen;
- die Lichtquellen der Szene.
Daneben wird beim Raytracing auch die Position eines Augpunktes sowie einer Bildebene angegeben, die zusammen die Perspektive angeben, aus der die Szene betrachtet wird. Der Augpunkt ist ein Punkt im Raum, der der Position einer virtuellen Kamera oder eines allgemeinen Beobachters entspricht. Die Bildebene ist ein virtuelles Rechteck, das sich in einiger Entfernung zum Augpunkt befindet. Sie ist die dreidimensionale Entsprechung des zu rendernden Rasterbildes im Raum. Rasterförmig verteilte Punkte auf der Bildebene entsprechen den Pixeln des zu erzeugenden Rasterbildes.
Verdeckungsberechnung
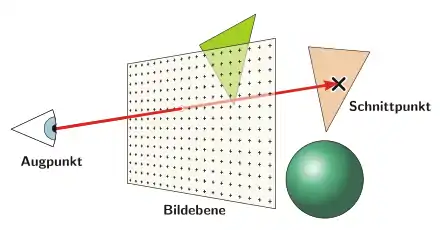

Raytracing ist in erster Linie ein Verfahren zur Verdeckungsberechnung, also zur Ermittlung der Sichtbarkeit von Objekten ab dem Augpunkt. Das Grundprinzip ist recht einfach.
Raytracing arbeitet mit einer Datenstruktur, Strahl genannt, die den Anfangspunkt und die Richtung einer Halbgeraden im Raum angibt. Es wird für jedes Pixel die Richtung des Strahls berechnet, der vom Augpunkt aus zum entsprechenden Pixel der Bildebene weist. Für jedes Primitiv der Szene wird nun mittels geometrischer Verfahren der eventuelle Schnittpunkt, bei dem der Strahl auf das Primitiv trifft, ermittelt. Dabei wird gegebenenfalls die Entfernung vom Augpunkt zum Schnittpunkt berechnet. Der „Gewinner“, also das vom Augpunkt aus sichtbare Primitiv, ist dasjenige mit der geringsten Distanz.
Das Prinzip der Aussendung der Strahlen vom Augpunkt aus ähnelt dem Aufbau einer Lochkamera, bei der ein Objekt auf einem Film abgebildet wird. Beim Raytracing sind allerdings „Film“ (Bildebene) und „Loch“ (Augpunkt) vertauscht. Ähnlich wie bei der Lochkamera bestimmt der Abstand zwischen Bildebene und Augpunkt die „Brennweite“ und damit das Sichtfeld.
Da die Strahlen nicht wie in der Natur von den Lichtquellen, sondern vom Augpunkt ausgehen, spricht man auch von Backward Ray Tracing. Raytracing beschäftigt sich mit der Frage, woher das Licht kommt. Einige Veröffentlichungen nennen das Verfahren allerdings Forward Ray Tracing oder Eye Ray Tracing.
Schnittpunkttests
Der oben erwähnte Test auf einen eventuellen Schnittpunkt von Strahl und Primitive ist das Herzstück des Raytracings. Solche Tests lassen sich für eine Vielzahl von Primitiventypen formulieren. Neben Dreiecken und Kugeln sind unter anderem Zylinder, Quadriken, Punktwolken oder gar Fraktale möglich.
Bei Kugeln ist der Schnittpunkttest eine relativ kurze und einfache Prozedur, was die Popularität dieser Objekte auf Raytracing-Testbildern erklärt. Viele Renderprogramme lassen jedoch aus Gründen der Einfachheit nur Dreiecke als Primitiven zu, aus denen sich jedes beliebige Objekt näherungsweise zusammensetzen lässt.
Seit Kurzem werden auch komplexere Geometrien für den Schnittpunkttest wie etwa NURBS verwendet.[8] Vorteilhaft dabei ist ein Maximum an Präzision, da die Fläche nicht wie sonst üblich in Dreiecke unterteilt wird. Der Nachteil ist eine erhöhte Renderzeit, da der Schnittpunkttest mit komplexen Freiformflächen sehr viel aufwändiger als mit einfachen Dreiecken ist. Eine hinreichende Annäherung an die Genauigkeit von NURBS ist zwar auch mit Dreiecken möglich, in diesem Fall muss aber eine sehr große Anzahl gewählt werden.
Shading
Bei der Ermittlung des nächsten Primitivs wird nicht nur der Schnittpunkt und seine Distanz zum Augpunkt, sondern auch die Normale des Primitivs am Schnittpunkt berechnet. Damit sind alle Informationen vorhanden, um die zum Augpunkt reflektierte „Lichtstärke“ und somit die Farbe zu ermitteln. Dabei werden auch die Beschreibungen der Lichtquellen der Szene genutzt. Den Berechnungen liegen lokale Beleuchtungsmodelle zugrunde, die die Materialbeschaffenheit eines Objekts simulieren. Diesen Teil des Renderers, der für die Ermittlung der Farbe zuständig ist, nennt man Shader.
Beispielcode
Die Programmierung eines einfachen Raytracers erfordert wenig Aufwand. In Pseudocode lässt sich das Prinzip folgendermaßen darstellen:
Prozedur Bild_Rendern
Strahl.Ursprung := Augpunkt
Für jedes (x,y)-Pixel der Rastergrafik
Strahl.Richtung := [3D-Koordinaten des Pixels der Bildebene] − Augpunkt
Farbe des (x,y)-Pixels := Farbe_aus_Richtung(Strahl)
Funktion Farbe_aus_Richtung(Strahl)
Schnittpunkt := Nächster_Schnittpunkt(Strahl)
Wenn Schnittpunkt.Gewinner = (kein) dann
Farbe_aus_Richtung := Hintergrundfarbe
sonst
Farbe_aus_Richtung := Farbe_am_Schnittpunkt(Strahl, Schnittpunkt)
Funktion Nächster_Schnittpunkt(Strahl)
MaxDistanz := ∞
Schnittpunkt.Gewinner := (kein)
Für jedes Primitiv der Szene
Schnittpunkt.Distanz := Teste_Primitiv(Primitiv, Strahl)
Wenn Schnittpunkt.Distanz < MaxDistanz dann
MaxDistanz := Schnittpunkt.Distanz
Schnittpunkt.Gewinner := Primitiv
Nächster_Schnittpunkt := Schnittpunkt
Jeder Raytracer, unabhängig von der verwendeten Raytracing-Variante, folgt einer ähnlichen Struktur, die noch einen Schnittpunkttest (Teste_Primitiv) und einen Shader (Farbe_am_Schnittpunkt) enthält.
Leistung
Beschleunigungstechniken
Bei der Bestimmung des ersten Primitivs, auf das ein Strahl trifft, kann, wie im weiter oben aufgeführten Beispielcode, jedes Primitiv der Szene gegen den Strahl getestet werden. Dies ist jedoch nicht grundsätzlich erforderlich, wenn bekannt ist, dass gewisse Primitive sowieso nicht in der Nähe des Strahls liegen und daher nicht getroffen werden können. Da Schnittpunkttests die größte Laufzeit beim Raytracing beanspruchen, ist es wichtig, so wenig Primitive wie möglich gegen den Strahl zu testen, um die Gesamtlaufzeit gering zu halten.
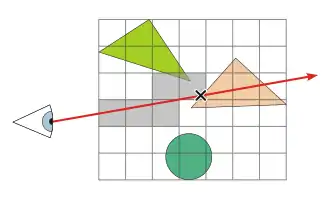
Bei den Beschleunigungsverfahren wird die Szene meist in irgendeiner Form automatisch aufgeteilt und die Primitiven diesen Unterteilungen zugewiesen. Wenn ein Strahl durch die Szene wandert, so wird er nicht gegen die Primitiven, sondern zunächst gegen die Unterteilungen getestet. Dadurch muss der Strahl nur noch gegen die Primitive derjenigen Unterteilung getestet werden, die der Strahl kreuzt.
Es wurde eine Vielzahl derartiger Beschleunigungstechniken für Raytracing entwickelt. Beispiele für Unterteilungsschemas sind Voxelgitter, BSP-Bäume sowie Bounding Volumes, die die Primitiven umschließen und eine Hierarchie bilden. Mischformen dieser Techniken sind ebenfalls populär. Auch für Animationen gibt es spezielle Beschleunigungstechniken. Die Komplexität dieser Techniken lassen einen Raytracer schnell zu einem größeren Projekt anwachsen.
Keine Technik ist generell optimal; die Effizienz ist szenenabhängig. Dennoch reduziert jedes Beschleunigungsverfahren die Laufzeit enorm und macht Raytracing erst zu einem praktikablen Algorithmus. Auf Kd-Bäumen basierende Unterteilungen sind für die meisten nicht-animierten Szenen die effizienteste oder nahezu effizienteste Technik, da sie sich mittels Heuristiken optimieren lassen.[9][10] Mehrfach festgestellt wurde, dass die asymptotische Laufzeit von Raytracing in Abhängigkeit von der Anzahl der Primitiven logarithmisch ist.
Es wurde gezeigt, dass auf modernen Rechnern nicht die Prozessorleistung, sondern Speicherzugriffe die Geschwindigkeit des Raytracings begrenzen. Durch sorgfältige Nutzung von Caching durch den Algorithmus ist es möglich, die Laufzeit wesentlich zu verringern. Ebenfalls möglich ist die Nutzung der SIMD-Fähigkeit moderner Prozessoren, die parallele Berechnungen ermöglicht, sowie speziell darauf optimierter Unterteilungsschemata.[11][12] Damit ist das gleichzeitige Verfolgen mehrerer, in „Paketen“ zusammengefasster, Strahlen möglich. Grund dafür ist, dass die vom Augpunkt ausgesendeten Strahlen meist sehr ähnlich sind, also meist die gleichen Objekte schneiden. Mit dem Befehlssatz SSE etwa können vier Strahlen gleichzeitig auf einen Schnittpunkt mit einem Primitiv getestet werden, was diese Berechnung um ein Vielfaches beschleunigt. Auf entsprechenden Hardwareimplementationen – zum Beispiel auf FPGAs – können auch größere Pakete mit über 1000 Strahlen verfolgt werden. Allerdings büßen Caching- und SIMD-Optimierungen bei erweiterten Formen des Raytracings viel von ihrem Geschwindigkeitsvorteil ein.
Weiterhin ist es möglich, den gesamten Raytracing-Vorgang zu parallelisieren. Dies lässt sich etwa dadurch trivial bewerkstelligen, dass verschiedene Prozessoren bzw. Maschinen unterschiedliche Ausschnitte des Bildes rendern. Lediglich gewisse Beschleunigungstechniken oder Erweiterungen müssen angepasst werden, um parallelisierungstauglich zu sein.
Speicherbedarf
Das grundlegende Raytracing-Verfahren benötigt kaum Speicher. Jedoch belegt die Szene selbst, die sich heutzutage bei komplexen Szenen oft aus mehreren Millionen Primitiven zusammensetzt, sehr viel Speicher und kann mehrere Gigabyte umfassen. Hinzu kommt der mehr oder weniger hohe zusätzliche Speicherbedarf der Beschleunigungstechniken. Da solch große Szenen nicht vollständig in den Arbeitsspeicher des Rechners passen, wird häufig Swapping nötig.
Bei größeren Objekten, die mehrmals in der Szene vorhanden sind und sich nur durch ihre Position und Größe unterscheiden (etwa bei einem Wald voller Bäume), muss nicht die gesamte Geometrie neu gespeichert werden. Durch diese Instancing genannte Technik lässt sich bei bestimmten Szenen erheblich Platz einsparen.
Erweiterungen
Einer der Gründe für den Erfolg des Raytracing-Verfahrens liegt in seiner natürlichen Erweiterbarkeit. Das oben beschriebene primitive Verfahren ist für die heutigen Anforderungen der Bildsynthese unzureichend. Mit steigender Rechenleistung und zunehmender Inspiration aus der Physik – vor allem der Optik und der Radiometrie – kamen mehrere Erweiterungen und Varianten auf, von denen einige hier kurz vorgestellt werden sollen.
Grundsätzlich gilt, dass mit jeder Erweiterung die erreichbare Qualität der gerenderten Bilder sowie der relative Zeitbedarf stark anstieg und mit Path Tracing das Maximum erreichte. Erst nachfolgende Entwicklungen zielten darauf ab, den Zeitaufwand von Path Tracing zu verringern, ohne an Qualität einzubüßen.
Schatten
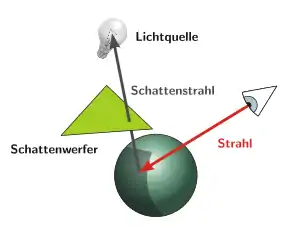
Aufgrund der Flexibilität des Raytracing-Algorithmus ist es möglich, Lichtstrahlen nicht nur vom Augpunkt, sondern auch von beliebigen anderen Punkten des Raums auszusenden. Wie Arthur Appel bereits 1968 demonstrierte, kann dies dazu benutzt werden, Schatten zu simulieren.
Ein beliebiger Punkt einer Oberfläche befindet sich genau dann im Schatten, wenn sich zwischen ihm und der Lichtquelle ein Objekt befindet. Indem vom Schnittpunkt an der Oberfläche ein Schattenstrahl in Richtung der Lichtquelle ausgesendet wird, lässt sich bestimmen, ob ein Objekt dessen Weg kreuzt. Ist dies der Fall, so befindet sich der Schnittpunkt im Schatten, und es wird als Helligkeit des Strahls 0 zurückgegeben. Im anderen Fall findet normales Shading statt.
Rekursives Raytracing

Raytracing lässt sich nicht nur auf einfache lichtundurchlässige, sondern auch auf durchsichtige und spiegelnde, reflektierende Objekte anwenden. Dabei werden weitere Lichtstrahlen von den Schnittpunkten ausgesendet. Bei spiegelnden Flächen etwa muss dabei lediglich die Richtung des von der Fläche ausgehenden Strahls gemäß dem Reflexionsgesetz (Einfallswinkel ist gleich Reflexionswinkel) berücksichtigt und ein entsprechender Reflexionsstrahl errechnet werden.
Bei lichtdurchlässigen Objekten wird ein Strahl gemäß dem Snelliusschen Brechungsgesetz ausgesendet, diesmal ins Innere des betreffenden Objektes. Generell reflektieren transparente Objekte auch einen Teil des Lichts. Die relativen Farbanteile des reflektierten und des gebrochenen Strahls lassen sich mit den Fresnelschen Formeln berechnen. Diese Strahlen werden auch Sekundärstrahlen genannt.
Da die Sekundärstrahlen auf weitere Objekte fallen können, wird der Algorithmus rekursiv aufgerufen, um mehrfache Spiegelungen und Lichtbrechungen zu ermöglichen. Die hierarchische Gesamtheit der Aufrufe wird auch Renderbaum genannt.
Rekursives Raytracing wurde um 1980 von Kay und Whitted entwickelt.[13][14]
In Pseudocode sieht der Shader beim rekursiven Raytracing in etwa wie folgt aus:
Funktion Farbe_am_Schnittpunkt(Strahl, Schnittpunkt)
Wenn Schnittpunkt.Gewinner.Material = spiegelnd oder transparent dann
Reflektierter_Anteil := Fresnel(Strahl, Schnittpunkt)
Farbe := Reflektierter_Anteil × Farbe_aus_Richtung(Reflexionsstrahl)
+ Gebrochener_Anteil × Farbe_aus_Richtung(Gebrochener Strahl)
sonst
Farbe := 0
Für jede Lichtquelle
Schattenstrahl := Lichtquelle.Position - Schnittpunkt.Position
SchattenSchnittpunkt := Nächster_Schnittpunkt(Schattenstrahl)
Wenn SchattenSchnittpunkt.Gewinner = Lichtquelle dann
Farbe := Farbe + Direkte_Beleuchtung(Strahl, Lichtquelle)
Farbe_am_Schnittpunkt := Farbe
Der Rest des Programms kann wie beim einfachen Raytracing bleiben. Die hier aufgerufene Funktion Farbe_aus_Richtung kann wiederum Farbe_am_Schnittpunkt aufrufen, woraus der rekursive Charakter des Verfahrens deutlich wird.
Diffuses Raytracing
Rekursives Raytracing ermöglicht neben Lichtbrechung und -reflexion die Simulation von harten Schatten. In Wirklichkeit haben Lichtquellen jedoch eine bestimmte Größe, was dazu führt, dass Schatten weich und verschwommen wirken.
Dieser Effekt, sowie Antialiasing, glänzende Reflexion und mehr, lassen sich mit diffusem Raytracing (auch stochastisches Raytracing oder distributed ray tracing genannt) simulieren, das 1984 von Cook u. a. veröffentlicht wurde.[15] Die Idee ist, in verschiedenen Situationen statt eines Strahls mehrere Strahlen auszusenden und aus den errechneten Farben den Mittelwert zu bilden. Beispielsweise lassen sich weiche Schatten mit Kern- und Halbschatten erzeugen, indem die Richtungen der Schattenstrahlen zufällig verteilt die Oberfläche der Lichtquelle abtasten.[16] Der Nachteil ist, dass dabei Bildrauschen entsteht, wenn zu wenig Strahlen verwendet werden. Es gibt jedoch Möglichkeiten wie Importance Sampling, die das Rauschen reduzieren.
Path Tracing und Light Ray Tracing

Obwohl diffuses Raytracing zahlreiche Effekte ermöglicht, ist es immer noch nicht in der Lage, die globale Beleuchtung mit Effekten wie diffuser Interreflexion und Kaustiken (durch Bündelung von Licht erzeugte helle Lichtflecken) zu simulieren. Dies liegt daran, dass zwar bei spiegelnden Reflexionen, nicht jedoch bei diffusen Oberflächen Sekundärstrahlen ausgesendet werden.
In seiner 1986 veröffentlichten Publikation beschrieb James Kajiya die Rendergleichung, die die mathematische Basis für alle Methoden der globalen Beleuchtung bildet.[17] Die von einem Strahl beigetragene „Helligkeit“ wird dabei radiometrisch korrekt als Strahldichte interpretiert. Kajiya zeigte, dass zur globalen Beleuchtung Sekundärstrahlen von allen Oberflächen ausgesendet werden müssen. Daneben wies er auch darauf hin, dass ein Renderbaum den Nachteil hat, dass zu viel Arbeit für die Berechnungen in großer Hierarchietiefe verschwendet wird und es besser ist, jeweils einen einzigen Strahl auszusenden. Diese Methode ist heute als Path Tracing bekannt, da ein Strahl sich vom Augpunkt aus seinen „Weg“ durch die Szene sucht. Path Tracing hat eine rigorose mathematische und physikalische Basis.
Falls beim Path Tracing der von einer diffusen Oberfläche ausgesandte Sekundärstrahl eine Lichtquelle direkt trifft, so wird dieser Helligkeitsanteil üblicherweise ignoriert. Der Anteil der direkten Beleuchtung wird stattdessen weiterhin per Schattenstrahl berechnet. Alternativ kann die direkte Beleuchtung berechnet werden, indem nur ein Sekundärstrahl gemäß dem lokalen Beleuchtungsmodell ausgesendet wird und, falls dieser eine Lichtquelle direkt trifft, deren Strahldichte zurückgegeben wird. Welche dieser beiden Methoden effizienter ist, hängt vom lokalen Beleuchtungsmodell der Oberfläche sowie vom von der Oberfläche betrachteten Raumwinkel der Lichtquelle ab.[18] Die konzeptuell einfachere Variante des Path Tracing, bei der keine Schattenstrahlen ausgesandt werden, ist als Adjoint Photon Tracing bekannt.[19]
Obwohl Path Tracing die globale Beleuchtung simulieren kann, nimmt die Effizienz des Verfahrens bei kleinen Lichtquellen ab. Insbesondere Kaustiken und deren Reflexionen sind mit Path Tracing sehr verrauscht, sofern nicht sehr viele Strahlen ausgesendet werden. Deshalb werden meist andere, auf Path Tracing basierende Verfahren oder Erweiterungen verwendet.
Light Ray Tracing ist eine seltene Variante, bei der die Lichtstrahlen nicht vom Augpunkt, sondern von den Lichtquellen ausgesendet werden. Die Pixel, die vom Strahl auf der Bildebene getroffen werden, werden eingefärbt. Dadurch lassen sich bestimmte Effekte wie Kaustiken gut, andere Effekte jedoch nur sehr ineffizient simulieren, da viele Strahlen die Bildebene verfehlen.
Weitere Entwicklungen
Da sich einige Effekte nur vom Augpunkt, andere nur von den Lichtquellen aus gut simulieren lassen, wurden Algorithmen entwickelt, die beide Methoden kombinieren. Das Ziel ist es, Szenen mit beliebig komplexer Lichtverteilung und -reflexion effizient rendern zu können.
- Bidirektionales Path Tracing,
- unabhängig voneinander 1993 und 1994 von Lafortune/Willems und E. Veach/Leonidas J. Guibas entwickelt, ist eine direkte Erweiterung des Path Tracing, bei der Strahlen sowohl vom Augpunkt als auch von den Lichtquellen aus gesendet und beide Pfade anschließend kombiniert werden.[20][21] Die Auftreffpunkte des Lichtpfades werden als punktförmige virtuelle Lichtquellen zur Beleuchtung des Augpfades herangezogen. Bidirektionales Path Tracing kann als Verallgemeinerung von Path Tracing, Adjoint Photon Tracing oder Light Ray Tracing betrachtet werden, da es den Lichtaustausch zwischen allen möglichen Kombinationen von Auftreffpunkten der beiden Pfade berücksichtigt. Das Verfahren bietet meist eine bessere Leistung als reines Path Tracing, vor allem bei der Berechnung von Kaustiken, beseitigt jedoch nicht vollständig dessen Probleme.
- Metropolis Light Transport (MLT)
- ist eine Erweiterung des bidirektionalen Path Tracing und wurde 1997 von Veach und Guibas vorgestellt.[22] Bei MLT werden die Lichtstrahlen so ausgesendet, dass sie sich der Beleuchtung anpassen und die Szene „erkunden“. Die Idee des Verfahrens ist es, „gute“ Pfadkombinationen, über die viel Energie transportiert wird, nach ihrem Auffinden nicht sofort wieder zu verwerfen, sondern weiterzuverwenden. MLT bietet oft deutliche Geschwindigkeitsvorteile und vernünftige Ergebnisse bei Szenen, die mit anderen (vorherigen) Algorithmen nur schwer korrekt zu simulieren sind. Ebenso wie Path Tracing und bidirektionales Path Tracing liefert MLT bei geeigneter Implementierung statistisch erwartungstreue Bilder, das heißt, die einzige Abweichung vom idealen Bild besteht im Bildrauschen; andere Fehler sind ausgeschlossen.

- Photon Mapping
- wurde 1995 von Jensen veröffentlicht.[23] Das Verfahren besteht im Aussenden von Partikeln von den Lichtquellen aus und deren Speicherung in einer speziellen, von der Geometrie unabhängigen Struktur. Dieser Algorithmus war insofern ein Durchbruch, als er es ermöglicht, die Beleuchtung in einem Vorbearbeitungsschritt zu speichern und diese während des Rendervorgangs relativ schnell zu rekonstruieren.
- Photon Mapping ist kein eigenständiges Rendering-Verfahren, sondern dient der Ergänzung von anderen Raytracing-Methoden – meistens, um diffuses Raytracing auf globale Beleuchtung zu erweitern. Allerdings ist Photon Mapping nicht erwartungstreu, in der Präzision schwer intuitiv kontrollierbar und weniger robust als MLT. Dies macht sich vor allem bei Szenen mit schwierigen Lichtverhältnissen bemerkbar.
Übersicht
| Raytracing-Verfahren | Schatten | Lichtreflexion / -brechung / -streuung | Beleuchtung | Beispielbild |
|---|---|---|---|---|
| Nur Verdeckungsberechnung | Keine | Keine | Keine |  |
| Simulation von Schatten (mit nur einem Schattenstrahl) |
Nur harte Schatten | Keine | Nur direkte Beleuchtung |  |
| Rekursives Raytracing | Nur harte Schatten | Nur bei spiegelnden / brechenden Oberflächen | Nur direkte Beleuchtung oder Spiegelung / Brechung |  |
| Diffuses Raytracing | Vollständig | Nur bei spiegelnden / brechenden Oberflächen | Nur direkte Beleuchtung oder Spiegelung / Brechung |  |
| Path Tracing (und nachfolgende Verfahren) |
Vollständig | Vollständig (auch diffus) | Vollständig (Globale Beleuchtung) |  |
Besonderes
Die angeführten gängigen Varianten des Raytracings lassen sich erweitern, um zusätzliche Effekte zu ermöglichen. Einige Beispiele:
- Constructive Solid Geometry (CSG)
- ist ein verbreitetes Modellierverfahren, bei dem Objekte aus anderen Objekten zusammengesetzt werden. Raytracing lässt sich relativ einfach um CSG-Funktionalität erweitern.[24]
- Texture Mapping
- sowie Displacement Mapping und Bumpmapping sind ebenfalls für Raytracing möglich. Bei letzterem Verfahren muss allerdings darauf geachtet werden, dass die erzeugten Reflexionsrichtungen stets vom Objekt weg weisen.
- Volumenstreuung
- ermöglicht die realistische Simulation teilweise durchscheinender und das Licht streuender Objekte. Dazu gehören beispielsweise Milch oder Blätter, aber auch das Himmelsblau und atmosphärische Bedingungen.
- Spektrales Rendering
- Die meisten gängigen Raytracer verwenden den RGB-Farbraum zur Darstellung von Farben, was nur eine Annäherung an das kontinuierliche Lichtspektrum darstellt und nicht immer physikalisch plausibel ist. Indem für die Farbe eine von der Wellenlänge des Lichts abhängige Repräsentation verwendet wird, lassen sich Effekte wie Metamerie und Dispersion simulieren. Auch Polarisation und Fluoreszenz sind möglich.[25]
- High Dynamic Range Rendering
- Indem die Farbwerte beim Raytracing durch Gleitkommazahlen berechnet und in HDR-Bildern mit hohem Kontrastumfang gespeichert werden, ist es möglich, Helligkeit und Kontrast von gerenderten Bildern nachträglich ohne Qualitätsverlust beliebig zu verändern. Beim Image-based Lighting wird die zu rendernde Szene von einem HDR-Bild umschlossen, was eine realistische Ausleuchtung durch aufgenommene Umgebungen ermöglicht.
- Relativistisches Raytracing
- Durch Berücksichtigung der Formeln für die spezielle Relativitätstheorie lassen sich die optischen Effekte, die bei gekrümmter Raumzeit auftreten, veranschaulichen.[26] Die Strahlverläufe werden hierbei unter Berücksichtigung der hohen Geschwindigkeiten und Massen modifiziert; außerdem ergeben sich Helligkeits- und Farbänderungen.
Einsatzgebiete
Computergrafik
Raytracing-Berechnungen gelten als sehr zeitintensiv. Raytracing wird daher vornehmlich bei der Erzeugung von Darstellungen eingesetzt, bei denen eher die Qualität als die Berechnungszeit im Vordergrund steht. Ein Bild mit Raytracing zu berechnen, kann abhängig von der verwendeten Technik, der Szenenkomplexität, der verwendeten Hardware und der gewünschten Qualität beliebig lange – in der Praxis oft mehrere Stunden, in Einzelfällen sogar mehrere Tage – dauern. In Bereichen wie der Virtuellen Realität, in der räumliche Darstellungen in Echtzeit berechnet werden müssen, konnte sich Raytracing daher bisher nicht durchsetzen. Computeranimationsfilme werden überwiegend mit dem REYES-System erzeugt, bei dem Raytracing-Berechnungen so weit wie möglich vermieden werden. Gelegentlich wurde Raytracing von der Demoszene genutzt.
Gegenüber üblichen Echtzeitrenderern auf Z-Buffer-Basis hat Raytracing jedoch mehrere Vorteile: eine einfache Implementierung mit überschaubarer Komplexität, eine im Gegensatz zur Grafikpipeline hohe Flexibilität sowie die leichtere Austauschbarkeit der Shader und dadurch eine erleichterte Implementierung neuer Shader. Die Geschwindigkeit von Raytracing muss daher in Relation zur erreichten Bildqualität gesetzt werden. Für die anspruchsvollen Qualitätsanforderungen der realistischen Bildsynthese gibt es, insbesondere bei komplizierten Szenen mit beliebigen Materialien, keine Alternative zu Raytracing.
Es existieren Bestrebungen, echtzeitfähige Raytracer für komplexe Szenen zu implementieren, was bereits unter bestimmten Voraussetzungen mit prozessor- und speicheroptimierten Softwarelösungen gelungen ist. Auf Hardware optimierte Implementierungen von Raytracing zeigen, dass die künftige breite Nutzung von Raytracing im Echtzeitbereich denkbar ist. Mit diesen Anwendungen beschäftigen sich Projekte wie die OpenRT-Programmierschnittstelle und diverse Implementierungen für programmierbare Grafikprozessoren (GPGPU). Außerdem wurden spezielle Architekturen für hardwarebeschleunigtes Raytracing entwickelt.[27]
Weitere Anwendungsgebiete

Das Raytracing-Prinzip kann auf beliebige Anwendungsbereiche ausgeweitet werden, bei denen die Ausbreitung von Wellen in einer Szene simuliert werden soll. Strahlen repräsentieren dabei stets die Normalenvektoren zu einer Wellenfront. In der Auralisation und Hochfrequenztechnik versucht man, die Auswirkungen einer Szene auf die Akustik beziehungsweise auf ein elektromagnetisches Feld zu simulieren. Das Ziel ist es, für bestimmte Frequenzen den Energieanteil zu berechnen, der von einem Sender zu einem Empfänger über die verschiedenen möglichen Wege durch die Szene übertragen wird.
In der Akustik ist Raytracing neben der Spiegelschallquellenmethode und der Diffusschallberechnung eine Möglichkeit zur Lösung dieses Problems. Zur Simulation müssen die Materialeigenschaften der verschiedenen Körper sowie die Dämpfung des Schalls durch die Luft berücksichtigt werden.
Eine Möglichkeit zum Auffinden der Übertragungswege besteht darin, Strahlen von einer Quelle isotrop (in alle Richtungen) auszusenden, eventuell mit Energieverlust an den Gegenständen zu reflektieren und die Gesamtenergie der auf den Empfänger auftreffenden Strahlen zu ermitteln. Diese Methode wird Ray launching genannt. Strahlen können auch eine bestimmte „Form“ – etwa die einer Röhre – haben, um punktförmige Empfänger simulieren zu können. Der Nachteil dieser Methode ist ihre Langsamkeit, da viele Strahlen nie den Empfänger erreichen und für präzise Statistiken eine hohe Anzahl vonnöten ist.
Ein weiteres Problem ergibt sich dadurch, dass die Wellenlänge oft nicht gegenüber den Abmessungen der Körper innerhalb einer Szene vernachlässigbar ist. Sofern die Beugung von Strahlen nicht berücksichtigt wird, kann es daher zu merklichen Fehlern in der Simulation kommen.
Literatur
- Philip Dutré, Philippe Bekaert, Kavita Bala: Advanced Global Illumination. AK Peters, Natick MA 2003, ISBN 1-56881-177-2 (advancedglobalillumination.com)
- Andrew S. Glassner: An Introduction to Ray tracing. Morgan Kaufmann, London 1989, ISBN 0-12-286160-4
- Andrew S. Glassner: Principles of Digital Image Synthesis. Morgan Kaufmann, London 1995, ISBN 1-55860-276-3
- Matt Pharr, Greg Humphreys: Physically Based Rendering. From Theory to Implementation. Morgan Kaufmann, London 2004, ISBN 0-12-553180-X (pbrt.org)
- Peter Shirley: Realistic Ray Tracing. AK Peters, Natick MA 2003, ISBN 1-56881-198-5
- Kevin G. Suffern: Ray Tracing from the Ground Up. AK Peters, Wellesley MA 2007, ISBN 978-1-56881-272-4
Weblinks
Anmerkungen
- Hans-Joachim Bungartz u. a.: Einführung in die Computergraphik: Grundlagen, geometrische Modellierung, Algorithmen, S. 135. Vieweg, Braunschweig 2002, ISBN 3-528-16769-6
- Beat Brüderlin, Andreas Meier: Computergrafik und Geometrisches Modellieren, S. 154. Teubner, Stuttgart 2001, ISBN 3-519-02948-0
- Terrence Masson: CG 101: A Computer Graphics Industry Reference. S. 267. Digital Fauxtography 2007, ISBN 0-9778710-0-2
- Arthur Appel: Some Techniques for Shading Machine Renderings of Solids. In Proceedings of the Spring Joint Computer Conference 1968. S. 37–45. AFIPS Press, Arlington
- Mathematical Applications Group, Inc.: 3-D Simulated Graphics Offered by Service Bureau. Datamation 13, 1 (Feb. 1968): 69, ISSN 0011-6963
- Robert Goldstein, Roger Nagel: 3-D Visual Simulation. Simulation 16, 1 (Jan. 1971): 25–31, ISSN 0037-5497
- Terrence Masson: CG 101: A Computer Graphics Industry Reference. In: Digital Fauxtography, 2007, ISBN 0-9778710-0-2, S. 162.
- Oliver Abert u. a.: Direct and Fast Ray Tracing of NURBS Surfaces. In Proceedings of IEEE Symposium on Interactive Ray Tracing 2006. S. 161–168. IEEE, Salt Lake City 2006, ISBN 1-4244-0693-5 (PDF, 700 kB (Memento vom 2. Dezember 2007 im Internet Archive))
- Vlastimil Havran u. a.: Statistical Comparison of Ray-Shooting Efficiency Schemes. Technical Report TR-186-2-00-14, Institute of Computer Graphics and Algorithms, Vienna University of Technology 2000 (ist.psu.edu)
- Ingo Wald, Vlastimil Havran: On building fast kd-trees for ray tracing, and on doing that in O(N log N). In Proceedings of IEEE Symposium on Interactive Ray Tracing 2006. S. 61–69. IEEE, Salt Lake City 2006, ISBN 1-4244-0693-5 (PDF, 230 kB)
- Ingo Wald u. a.: Interactive Rendering with Coherent Ray Tracing. Computer Graphics Forum 20, 3 (Sep. 2001), S. 153–164, ISSN 0167-7055 ( graphics.cs.uni-sb.de (Memento vom 5. Juni 2005 im Internet Archive))
- Alexander Reshetov u. a.: Multi-Level Ray Tracing Algorithm. ACM Transactions on Graphics 24, 3 (July 2005): 1176–1185, ISSN 0730-0301 (PDF; 400 kB)
- Douglas Scott Kay: Transparency, Refraction and Ray Tracing for Computer Synthesized Images. Thesis, Cornell University, Ithaca 1979
- Turner Whitted: An Improved Illumination Model for Shaded Display. Communications of the ACM 23, 6 (June 1980): 343–349, ISSN 0001-0782 (PDF, 4,6 MB)
- Robert Cook u. a.: Distributed ray tracing. ACM SIGGRAPH Computer Graphics 18, 3 (July 1984), S. 137–145, ISSN 0097-8930
- Peter Shirley, Changyaw Wang, Kurt Zimmermann: Monte Carlo Techniques for Direct Lighting Calculations. ACM Transactions on Graphics 15, 1 (Jan. 1996), S. 1–36 (PDF; 400 kB)
- James Kajiya: The Rendering Equation. ACM SIGGRAPH Computer Graphics 20, 4 (Aug. 1986), S. 143–150, ISSN 0097-8930
- Eric Veach, Leonidas J. Guibas: Optimally combining sampling techniques for Monte Carlo rendering. In SIGGRAPH ’95 Proceedings, S. 419–428. ACM, New York 1995, ISBN 0-89791-701-4 (graphics.stanford.edu)
- R. Keith Morley u. a.: Image synthesis using adjoint photons. In Proceedings of Graphics Interface 2006, S. 179–186. Canadian Information Processing Society, Toronto 2006, ISBN 1-56881-308-2 (PDF, 4,7 MB)
- Eric Lafortune, Yves Willems: Bi-Directional Path Tracing. In Proceedings of Compugraphics ’93. S. 145–153. Alvor 1993 (graphics.cornell.edu)
- Eric Veach, Leonidas Guibas: Bidirectional Estimators for Light Transport. In Eurographics Rendering Workshop 1994 Proceedings. S. 147–162. Darmstadt 1994 (graphics.stanford.edu)
- E. Veach, L.J. Guibas: Metropolis Light Transport. In SIGGRAPH ’97 Proceedings. S. 65–76. ACM Press, New York 1997, ISBN 0-89791-896-7 (graphics.stanford.edu)
- Henrik Wann Jensen and Niels Jørgen Christensen: Photon Maps in Bidirectional Monte Carlo Ray Tracing of Complex Objects. Computers and Graphics 19, 2 (Mar. 1995): 215–224, ISSN 0097-8493 (graphics.stanford.edu)
- Peter Atherton: A Scan-line Hidden Surface Removal Procedure for Constructive Solid Geometry. ACM SIGGRAPH Computer Graphics 17, 3 (July 1983), S. 73–82, ISSN 0097-8930
- Alexander Wilkie u. a.: Combined Rendering of Polarization and Fluorescence Effects. In Proceedings of the 12th Eurographics Workshop on Rendering Techniques. Springer, London 2001, ISBN 3-211-83709-4, S. 197–204 (PDF, 2,9 MB)
- Daniel Weiskopf u. a.: Real-World Relativity: Image-Based Special Relativistic Visualization. In IEEE Visualization: Proceedings of the Conference on Visualization 2000. S. 303–310. IEEE Computer Society Press, Salt Lake City 2000, ISBN 1-58113-309-X (PDF, 640 kB (Memento vom 13. Juni 2007 im Internet Archive))
- Jörg Schmittler u. a.: SaarCOR – A Hardware Architecture for Ray Tracing. In Proceedings of the SIGGRAPH/EUROGRAPHICS Conference On Graphics Hardware. S. 27–36. Eurographics, Aire-la-Ville 2002, ISBN 1-58113-580-7 (PDF, 1,0 MB (Memento vom 28. Juli 2007 im Internet Archive))