Binary Space Partitioning

Binary Space Partitioning (BSP; deutsch binäre Raumpartitionierung oder BSP-Baum) ist eine Technik in der Informatik zur Partitionierung multidimensionaler Daten durch eine Menge von Hyperebenen. Die so erstellte Datenstruktur ist ein Binärbaum und wird BSP-Baum genannt.

Die wohl verbreitetste Anwendung von BSP-Bäumen ist die räumliche Unterteilung geometrischer Objekte. BSP findet vor allem Verwendung bei Grafik-Engines von Computerspielen für Objekte oder Teile der „Welt“, die sich während des Spiels geometrisch nicht mehr verändern. Eine weitere Anwendung findet sich beim Raytracing.

Ein Spezialfall der BSP-Bäume sind k-d-Bäume, oft auch als axis-aligned BSP-Trees (achsenparallele BSP-Bäume) bezeichnet. Bei kd-Bäumen sind die unterteilenden Hyperebenen immer entlang der Achsen des Koordinatensystems ausgerichtet.

Verfahren

Beim BSP wird der gesamte Raum anfangs durch eine (zunächst beliebig wählbare) Teilungsebene in zwei Teile geteilt. Für beide Halbräume wird dann das gleiche gemacht wie zuerst mit dem gesamten Raum, das heißt, die Welt wird rekursiv immer weiter unterteilt. Jeder innere Knoten des Binärbaumes repräsentiert somit eine Teilungsebene, während die zwei Teilbäume eines inneren Knotens dann jeweils einen Teil des Raums repräsentieren. Das Ende der Unterteilung ist meist dann erreicht, wenn in einem Teilraum nur mehr ein Datenelement der Ausgangsmenge (z. B. ein geometrisches Grundobjekt wie ein Dreieck oder Polygon) vorhanden ist.

Die Teilungsebenen fallen aus praktischen Gründen oft mit den Polygonen der geometrischen Objekte zusammen. Beim Erstellen des BSP-Baums wird dann ein Polygon aus dem aktuellen Teilraum gewählt, mit dessen Ebene der Teilraum weiter unterteilt wird. Dabei wird einerseits darauf geachtet, dass sich ungefähr gleich viele Polygone auf jeder Seite der gewählten Ebene befinden, andererseits, dass möglichst wenige Polygone des Teilraumes durch die Ebene zerschnitten werden, weil das Zerschneiden zu mehr Polygonen führt, wodurch sich die benötigte Zeit erhöht, um z. B. die Polygone zu zeichnen. Ziel bei der Erstellung des BSP-Baumes ist es, einen Baum zu erzeugen, welcher bei der späteren Traversierung ein optimales Laufzeitverhalten aufweist. Üblicherweise wird versucht, dies durch die Erzeugung eines balancierten Baumes zu erreichen.

Die Daten der Ausgangsmenge können entweder ausschließlich in den Blättern des Baumes oder sowohl in den Blättern als auch in den inneren Knoten gespeichert sein – beispielsweise, indem das Polygon, das zur Teilung verwendet wurde, einem der beiden entstandenen Teilräumen zugeschlagen wird oder direkt im gleichen Datenelement wie die Ebene gespeichert wird. Man nennt den BSP-Baum dann leaf-based („blattbasiert“) bzw. node-based („knotenbasiert“).

Anwendungen und Alternativen

Durch die BSP-Technik können viele Berechnungen, wie Kollisionserkennung oder die Verdeckungsberechnung von Polygonen, wesentlich schneller erfolgen. Beispiele für die Verwendung von Binary Space Partitioning in Computerspielen sind die Game Engines von Doom (dabei handelt es sich um zweidimensionales BSP, d. h. die Teilungsebenen sind eigentlich Teilungsgeraden), der Quake-Serie und von Doom 3.

Beim Raytracing werden BSP-Bäume als Beschleunigungstechnik verwendet, um nur bei möglichst wenigen Primitiven einen Schnittpunkttest durchzuführen.

Weitere Methoden zur hierarchischen Unterteilung des Raumes sind Quadtrees und Octrees.

Algorithmus für eine Liste von Polygonen

Der folgende rekursive Algorithmus erstellt einen BSP-Baum für eine Liste von Polygonen in der Ebene:[1]

Wähle ein Polygon P aus der Liste aus.
Erzeuge einen Knoten N im BSP-Baum und füge P in die Liste der Polygone an diesem Knoten hinzu.
Führe für jedes andere Polygon in der Liste folgende Schritte aus:
- Wenn dieses Polygon vollständig vor der Ebene liegt, die P enthält, verschiebe dieses Polygon in die Liste der Knoten vor P.
- Wenn dieses Polygon vollständig hinter der Ebene liegt, die P enthält, verschiebe dieses Polygon in die Liste der Knoten hinter P.
- Wenn dieses Polygon von der Ebene geschnitten wird, die P enthält, teile es in zwei Polygone auf und verschiebe sie in die jeweiligen Listen von Polygonen hinter und vor P.
- Wenn dieses Polygon in der Ebene mit p liegt, fügen Sie es der Liste der Polygone an Knoten N hinzu.
Wende diesen Algorithmus auf die Liste der Polygone vor P an.
Wende diesen Algorithmus auf die Liste der Polygone hinter P an.

Die Abbruchbedingung für die Rekursion ist erreicht, wenn die Liste der Polygone vor P oder die Liste der Polygone hinter P leer ist.

Beispiel 1

Aufbauen des Baumes

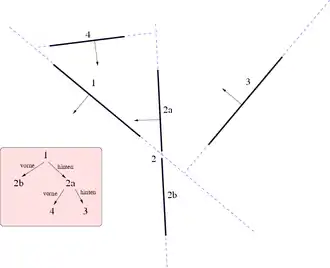
(Abbildung 1)Beispiel für eine Zerlegung mit vier Strecken

In Abbildung 1 ist ein Beispiel für die Zerlegung eines Raumes mit vier Strecken zu sehen. In dem rötlichen Kasten sieht man den daraus resultierenden binären Baum.

Zunächst teilt Strecke 1 den Raum in zwei Halbräume (gekennzeichnet durch die blau gestrichelte Linie) und die Strecke 2 in die beiden Teilstrecken 2a und 2b. Die Orientierung der Normalen der Strecken klassifiziert die beiden Halbräume nun als einen Halbraum vor der Strecke und einen Halbraum dahinter. Folglich werden die (Teil)-Strecken, die sich davor befinden in den linken, die, die sich dahinter befinden, in den rechten Teilbaum des Baumes eingefügt und mit den beiden entstehenden Halbräumen fortgefahren.

Betrachtet man zunächst die Strecke 2b, so teilt diese den Raum wieder in zwei Halbräume vor Strecke 1. Jedoch befindet sich keine weitere Strecke im selben Halbraum vor ihr (Strecke 4 wurde durch die Zerlegung von Strecke 1 in den Bereich hinter Strecke 1 „verbannt“). Hinter Strecke 2b befindet sich mit der gleichen Argumentation ebenfalls nichts mehr, das in den Baum eingeordnet werden müsste und das Verfahren terminiert für diesen Teilbaum.

Strecke 2a hingegen teilt den Raum wieder in zwei Teilräume und Strecke 4 wird in den Halbraum davor, Strecke 3 in den Halbraum dahinter eingeordnet.

Die Strecken 3 und 4 zerteilen den Raum zwar erneut in jeweils wieder zwei Halbräume, fügen jedoch nichts weiter in den Baum ein, so dass der Baum im rötlichen Kasten entstanden ist.

Durchlauf des Baumes

Nimmt man nun den Betrachter dort an, wo sich der Kasten mit dem BSP-Baum befindet (die Blickrichtung ist hier nicht weiter wichtig), so ergibt sich die Durchlauf- und damit Zeichenreihenfolge der Strecken wie folgt:

Beginnend von der Wurzel (Knoten 1), werden zunächst die Knoten, die vom Betrachter aus gesehen hinter dieser Strecke liegen, gezeichnet, anschließend die Strecke selbst und danach die Strecken, die sich vor der Strecke – also auf der Seite des Betrachters – befinden.

Im vorliegenden Fall sieht der Durchlauf des Baumes wie folgt aus:

3, 2a, 4, 1, 2b

Zunächst betritt man den Baum über die Wurzel (1). Nun muss man zunächst alle Strecken hinter der Strecke 1 zeichnen und begibt sich also in den rechten Teilbaum und landet dort bei der Wurzel 2a. Nun muss man auch dort erst die Knoten hinter dieser Wurzel zeichnen und steigt wieder in den rechten Teilbaum ab und landet beim Knoten 3. Dieser ist ein Blatt und kann sofort ausgegeben werden. Danach wird Strecke 2a gezeichnet und anschließend die Knoten davor – also 4. Nun ist auch dieser Teilbaum abgearbeitet und man zeichnet schließlich die Knoten 1 und 2b.

Beispiel 2

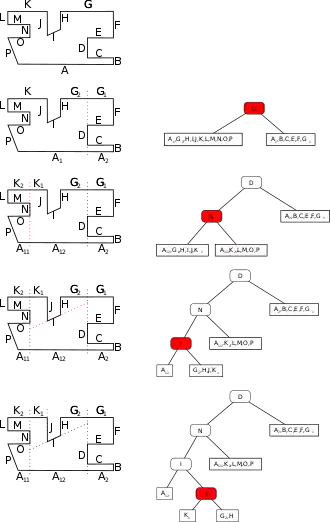
Beispiel für eine mögliche Zerlegung eines Objektes mittels eines BSP-Baumes.

In der Computergrafik wird der BSP-Baum häufig auch zum Speichern von Informationen über die Geometrie eines Objektes benutzt. Derartige BSP-Bäume werden manchmal als leaf-storing BSP trees bezeichnet, da die Informationen vorrangig in den Blättern abgelegt werden. Die nebenstehende Abbildung beschreibt die Erstellung eines solchen Baumes. Es ist zu beachten, dass die Normale der Kanten (werden für die Zuordnung auf der Vorder- oder Rückseite) alle in Richtung inneres des Objektes (Raumes) zeigen.

Aufbauen des Baumes

Zu Beginn wird das Objekt an einer beliebigen Kante, hier die Kante D, unterteilt und als Wurzel für den BSP-Baum benutzt. Es ist zu beachten, dass die Auswahl der Startkante mit entscheidend für die spätere Traversierungsgeschwindigkeit ist, welche deutlich besser bei einem balancierten Baum ist. Im Folgenden werden alle verbleibenden Kanten in vor bzw. hinter dem Knoten D gelegen eingeteilt. Für diese Entscheidung wird häufig, wie auch hier, die Normale der Gerade genommen, welche in Richtung vor dem Objekt zeigt. Wie bereits zuvor erwähnt, zeigen alle Normalen der Kanten in diesem Beispiel in das Innere des Objektes. Wie in diesem ersten Schritt zu sehen ist, wird die Kante A und die Kante G in jeweils zwei Teile unterteilt, da diese sich mit der ins Unendliche verlängerten Kante D schneiden. Damit ergibt sich der aktuelle Baum:

                           D
                         /   \
  A₁,G₂,H,I,J,K,L,M,N,O,P     A₂,B,C,E,F,G₁

Im Folgenden werden nun die Teilbäume wieder unterteilt. In dem Beispiel der Teilbaum: A₁,G₂,H,I,J,K,M,N,O,P. Es wird die Kante N ausgewählt und die restlichen Kanten des Teilbaumes wieder entsprechend in Vorder- und Rückseite der Kante N eingeteilt. Auch in diesem Schritt müssen wieder Kanten (Kante A₁ und Kante K) unterteilt werden. Das Teilstück A₁ der Kante A wird noch einmal in zwei Teile unterteilt. Damit ergibt sich der aktuelle Baum:

                         D
                       /   \
                      N     A₂,B,C,E,F,G₁
                    /   \
      A₁₂,G₂,H,I,J,K₁    A₁₁,K₂,L,M,O,P

Unter der Verwendung der Kante I wird der linke Teilbaum unterhalb von Knoten N wieder nach oberem Schema unterteilt. Dies ergibt den folgenden Baum:

                         D
                       /   \
                      N     A₂,B,C,E,F,G₁
                    /   \
                   I    A₁₁,K₂,L,M,O,P
                 /   \
               A₁₂    G₂,H,J,K₁

Da der linke Teilbaum nur ausschließlich aus dem Knoten A₁₂ besteht, kann der linke Ast nicht weiter unterteilt werden, und somit wird der rechte Zweig vom Knoten I abgearbeitet. Es wird die Kante J für die Unterteilung gewählt und die Kanten in diesem Teilraum entsprechend wieder in linker und rechter Teilbaum eingeordnet. Hieraus ergibt sich der folgende Baum:

                         D
                       /   \
                      N     A₂,B,C,E,F,G₁
                    /   \
                   I    A₁₁,K₂,L,M,O,P
                 /   \
               A₁₂    J
                    /   \
                  K₁     G₂,H

Nachdem nun der linke Teilbaum unter Knoten J vollständig verarbeitet wurde, der linke Teilbaum besteht nur aus einem Knoten, hier K₁, wird mit dem rechten Teilbaum fortgefahren. Es wird Kante H gewählt und der resultierende Baum sieht folgendermaßen aus:

                         D
                       /   \
                      N     A₂,B,C,E,F,G₁
                    /   \
                   I    A₁₁,K₂,L,M,O,P
                 /   \
               A₁₂    J
                    /   \
                  K₁     H
                       /
                     G₂

Identisch wird für alle weiteren Teilbäume, welche mehr als einen Kind-Knoten besitzen, vorgegangen. Am Ende wäre eine mögliche Lösung für den BSP-Baum:

                   D
                /     \
               /       \
              /         \
             /           \
            /             \
           /               \
          /                 \
         N                   E
       /    \               /  \
      /      \             /    \
     /        \           /      \
    /          \         /        \
   I            O       F          C
  /  \         / \     /          /
A₁₂   J       P    L  G₁         B
     / \     /    /            /
    K₁  H   A₁₁   M            A₂
       /        /
      G₂       K₂

Es ist zu beachten, dass der vorhergehend erstellte BSP-Baum nur eine mögliche Lösung darstellt. Da eine Kante für die Unterteilung des Baumes gewählt werden muss, beginnend mit der Kante für die Wurzel, hin zu einer Kante für die Unterteilung der Kinder eines jeden Knotens, kann eine Vielzahl von BSP-Bäumen konstruiert werden, welche den Raum korrekt unterteilen. Je nach Anwendung, kann die Leistungsfähigkeit im Hinblick auf Traversierung der verschiedenen BSP-Bäume stark schwanken. In den meisten Fällen, wird versucht, die Erzeugung eines entarteten Baumes zu vermeiden.

Siehe auch

Literatur

Henry Fuchs u. a.: On Visible Surface Generation by A Priori Tree Structures. In SIGGRAPH ’80 Proceedings, S. 124–133. ACM, New York 1980, ISBN 0-89791-021-4
Christer Ericson: Real-Time Collision Detection (The Morgan Kaufmann Series in Interactive 3-D Technology). Verlag Morgan Kaufmann, S. 349–382, Jahr 2005, ISBN 1-55860-732-3

Weblinks

BSP FAQ (englisch)
Java-Applet zu BSP

Einzelnachweise

GeeksforGeeks: Binary Space Partitioning

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] GeeksforGeeks: Binary Space Partitioning