Brennweite

Die Brennweite ist der Abstand zwischen der Hauptebene einer optischen Linse oder eines gewölbten Spiegels und dem Fokus (Brennpunkt).

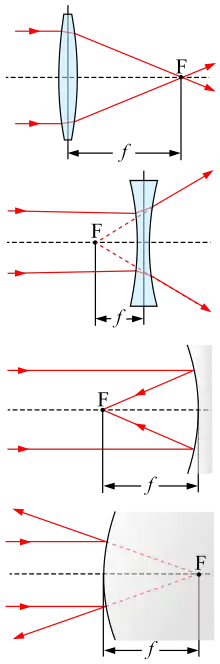
Eine Sammellinse konzentriert ein parallel einfallendes Strahlenbündel im nach ihr liegenden Brennpunkt (Abbildung rechts, erstes Bild).
Bei Zerstreuungslinsen liegt der Fokus vor der Linse, und ein parallel einfallendes Strahlenbündel wird so zerstreut, als ob die Einzelstrahlen alle aus diesem Fokus stammten (zweites Bild).
Bei einem Hohlspiegel läuft ein parallel einfallendes Strahlenbündel im vor dem Spiegel liegenden Brennpunkt zusammen (drittes Bild).
Bei einem Konvexspiegel wird ein parallel einfallendes Strahlenbündel so zerstreut, als ob die Einzelstrahlen alle aus dem hinter dem Spiegel liegenden Fokus stammten (viertes Bild).

Bei einzelnen dünnen Linsen ist die Brennweite f gleich dem Abstand des Brennpunkts F von der Linsenmitte. Bei gewölbten Spiegeln ist es der Abstand vom Spiegelscheitel.

Aus mehreren Linsen oder/und Spiegeln bestehende Systeme – wie zum Beispiel Objektive von Kameras oder Mikroskopen – haben analog definierte Brennweiten. Hierbei lassen sich die Lagen der Hauptebenen (zwei pro System) nicht so einfach wie bei einer Einzellinse (in ihr) oder bei einem Einzelspiegel (auf seinem Scheitel) angeben.

Die Brennweite ist ein Konzept der paraxialen Optik.[1] Sie bezieht sich daher nur auf Strahlen, die einen kleinen Winkel und einen kleinen Abstand zur optischen Achse des Abbildungssystems aufweisen.

Große Brennweiten entstehen durch flache, schwach gekrümmte Oberflächen. Kleine Brennweiten entstehen durch starke Krümmungen. Speziell bei einzelnen Linsen wird der Kehrwert der Brennweite Brechkraft oder Brechwert genannt. Bei Sammellinsen und Hohlspiegeln ist die Brennweite als positiver Wert, bei Zerstreuungslinsen und Konvexspiegeln als negativer Wert definiert.

Die Brennweite wird bei der Anwendung der Linsengleichung gebraucht. In der Fotografie bestimmt die Brennweite des Objektivs zusammen mit dem Aufnahmeformat den Bildwinkel (siehe auch Formatfaktor). Das gilt auch für das Zwischenbild beim Mikroskop. Bei Fernrohren und Ferngläsern bestimmen die Brennweiten von Objektiv und Okular zusammen die Vergrößerung.

Brechkraft

Der Kehrwert $D={\frac {1}{f}}$ der Brennweite $f$ wird Brechkraft genannt. Er wird bei Brillengläsern in Dioptrie angegeben.

Messung der Brennweite

Direkte Messung der Brennweite einer Lupe über das Bild eines Fensters im Rauminneren: Weit entfernte Gegenstände (hier: die Häuser) werden scharf, wenn sich die Linse im Abstand ihrer Brennweite von der Projektionsfläche befindet.

Gemäß der Abbildungsgleichung ist bei einer scharfen optischen Abbildung durch eine dünne Linse der Kehrwert der Brennweite gleich der Summe der Kehrwerte der Gegenstandsweite $g$ und der Bildweite $b$ :

{\frac {1}{f}}={\frac {1}{b}}+{\frac {1}{g}}

Dies kann ausgenutzt werden, um die Brennweite der Linse zu bestimmen. Wenn der abgebildete Gegenstand sehr weit entfernt ist, wird der Zusammenhang besonders einfach. Die Brennweite ist näherungsweise gleich groß wie die Bildweite und kann direkt aus dem Abstand des Bildes von der Linse abgelesen werden.

Ein Verfahren, das ohne ein weit entferntes Objekt auskommt, ist die Autokollimation. Dabei wird das weit entfernte Objekt durch einen planen Spiegel ersetzt. Das Bessel-Verfahren zur Bestimmung der Brennweite von dünnen Linsen nutzt aus, dass bei festem Abstand zwischen Objekt und Bild zwei Stellungen der Linse eine scharfe Abbildung erzeugen. Aus dem Abstand dieser beiden Positionen und dem Abstand zwischen Objekt und Bild lässt sich dann die Brennweite der Linse berechnen.

Bei dicken Linsen und Abbildungssystemen mit mehreren optischen Komponenten kann der Abstand der Hauptebenen meist nicht vernachlässigt werden. Dann kann das Abschätzen des Vergrößerungsverhältnisses genauere Ergebnisse liefern. Mit dem Abbe-Verfahren wird ein Satz von Positionen aufgenommen, in denen das Abbildungssystem Objekte scharf abbildet. Diese Punkte erfüllen eine Geradengleichung. Aus den Parametern der Geraden lassen sich die Brennweite und die Lage der Hauptebenen bestimmen.

Brillenoptiker bestimmen die Brennweite asphärischer Gläser und die über die Fläche variierende Brechkraft von Gleitsichtgläsern durch eine Wellenfrontanalyse. Dabei kommt meist ein Hartmann-Shack-Sensor zum Einsatz. Die automatisierten Geräte heißen aus historischen Gründen Scheitelbrechwertmesser.

Berechnung der Brennweite

Brechende Fläche

Als brechende Fläche bezeichnet man die Grenzschicht zwischen zwei optischen Medien mit unterschiedlichen Brechungsindizes. Kommt der Lichtstrahl von links, so sei $n$ der Brechungsindex auf der linken Seite und $n'$ der Brechungsindex auf der rechten Seite der Grenzfläche. Die Krümmung der Grenzfläche wird durch den Krümmungsradius $r$ beschrieben. Liegt der Mittelpunkt des Kreises, der die Grenzfläche beschreibt, auf der vom einfallenden Licht abgewandten Seite, so ist $r$ positiv, andernfalls negativ. Eine nicht gekrümmte Grenzfläche hat den Krümmungsradius $r=\infty$ .

f'=r{\frac {n'}{n'-n}}

Die Brennweite der anderen Seite wird durch Vertauschen der Brechungsindices gewonnen, da das Licht nun von rechts kommend aus $n$ nach $n'$ übertritt:

f=r{\frac {n}{n-n'}}=-r{\frac {n}{n'-n}}

Linse

Brennpunkt und bildseitige Hauptebene für zwei Flächen

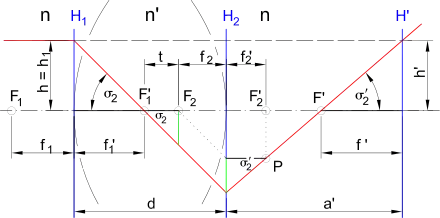
Die Brechung einer Linse der Dicke $d$ ist, z. B. mittels Matrizenoptik, aus den Brechungen ihrer beiden sphärischen Grenzflächen berechenbar. Mit den Brennweiten $f'_{2},f_{2}$ und $f'_{1},f_{1}$ der beiden Flächen und deren Abstand $d$ ergibt sich

f'={\frac {f'_{1}f'_{2}}{d-f'_{1}-f_{2}}}

für die bildseitige Brennweite der Linse. Mit den obigen Gleichungen der Flächenbrennweiten erhält man mit

{\frac {1}{f'}}={\frac {n'-n}{n}}\left({\frac {1}{r_{1}}}-{\frac {1}{r_{2}}}\right)+{\frac {(n'-n)^{2}d}{n'nr_{1}r_{2}}}

die bildseitige Linsenbrennweite in Abhängigkeit von den Krümmungsradien $r_{1},r_{2}$ und den Brechungsindizes $n$ und $n'$ . Wie in nebenstehender Abbildung wird die Brennweite $f$ von der Hauptebene H’ gemessen. Gegenstandsseitige und bildseitige Brennweiten haben die gleiche Größe, wenn die Linse auf beiden Seiten an Medien mit gleichem Brechungsindex $n$ grenzt, siehe auch Linsenschleiferformel.

Dünne Linse

Die Näherung $d\ll f$ ist für $d\approx 0$ erfüllt. Diese Näherung bezeichnet man als dünne Linse, und die Hauptebenen der beiden Grenzflächen fallen zusammen (und zwar zur Mittelebene). Die Gleichung für die Brennweite vereinfacht sich zu

{\frac {1}{f'}}={\frac {1}{f}}={\frac {n'-n}{n}}\left({\frac {1}{r_{1}}}-{\frac {1}{r_{2}}}\right),

wobei wieder von der Mittelebene weg gemessen wird.

In der geometrischen Optik heißt $D_{1}={\frac {n'-n}{nr_{1}}}$ Vorderflächenbrechwert und $D_{2}={\frac {n-n'}{nr_{2}}}$ Rückflächenbrechwert. Obige Gleichung lässt sich damit auch in der Form

D=D_{1}+D_{2}

schreiben.[2] Die optische Wirkung von Brillengläsern wird durch den Scheitelbrechwert ausgedrückt.

System aus zwei dünnen Linsen

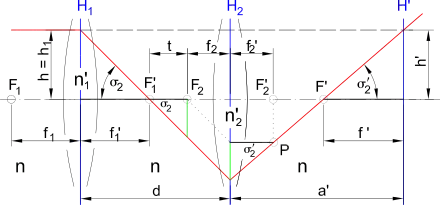
System aus zwei dünnen Linsen (H₁ und H₂)
Konstruktion des bildseitigen Brennpunkts F’ und der bildseitigen Hauptebene H’

Das System aus zwei dünnen Linsen ist dem System „Linse aus zwei brechenden Flächen“ prinzipiell ähnlich (vgl. nebenstehende Abbildung mit der darüberstehenden). Wenn beide Linsen beidseitig vom gleichen Medium umgeben sind, dann gilt:

{\frac {1}{f'}}={\frac {1}{f'_{1}}}+{\frac {1}{f'_{2}}}-{\frac {d}{f'_{1}\cdot f'_{2}}}={\frac {1}{f_{1}}}+{\frac {1}{f_{2}}}-{\frac {d}{f_{1}\cdot f_{2}}}={\frac {1}{f}}

Außer der Gleichheit der gegenstands- und bildseitigen Brennweiten der Einzellinsen gilt also auch die entsprechende Gleichheit beim System:

f'=f

Zur Abhängigkeit der Brennweiten des Linsensystems aus zwei dünnen Linsen von den Brechungsindizes und Krümmungsradien gelangt man, wenn man für $f_{1}$ und $f_{2}$ die oben angegebenen Linsenschleiferformeln für dünne Linsen anwendet.

Eng benachbarte dünne Linsen

Beim Zusammenrücken der dünnen Linsen wird im Grenzfall $d\ll f_{1},f_{2}$ . Der Abstand $d$ kann vernachlässigt werden. Die Brennweite eines solchen Systems ist näherungsweise gleich

{\frac {1}{f'}}={\frac {1}{f}}={\frac {1}{f_{1}}}+{\frac {1}{f_{2}}}.

Diese Gleichung wird zum Beispiel für zwei dünne, zusammengekittete Linsen verwendet. Eine solche Doppellinse besteht in der Regel aus zwei verschiedenen Glassorten, womit geringere Abbildungsfehler als bei einer aus nur einer Glassorte bestehenden Linse mit gleicher Brennweite erreicht werden, wie beispielsweise beim Achromaten.

Brennweite in der Fotografie

Aus Brennweite und Aufnahmeformat (bzw. Sensorgröße) ergibt sich in der Fotografie der Bildwinkel.[3] Je größer die Brennweite ist, desto kleiner ist der Bildwinkel (Bildausschnitt) (bei gleichbleibendem Aufnahmeformat) und umgekehrt.

Bei manchen Objektiven wird eine Brennweite angegeben, die beim Kleinbildformat (bei digitalen Kameras oft „Vollformat“ genannt) denselben Bildwinkel ergibt. Dabei wird der Formatfaktor bereits eingerechnet und es ergibt sich in Anbetracht unterschiedlicher Sensorgrößen eine einheitliche Bezugsgröße. Diese bezieht sich aber nur auf den Bildwinkel (siehe Formatfaktor).

Objektive unterschiedlicher Brennweite werden meist in drei Kategorien unterteilt, die jeweils unterschiedliche fotografische Wirkungen haben. Eine Brennweite, die etwa der Diagonalen des Aufnahmeformats entspricht, wird als Normalbrennweite bezeichnet. Objektive mit einer Brennweite von ca. 40 bis 55 mm bezeichnet man für das Kleinbildformat als Normalobjektive. Diese Brennweiten haben das Merkmal, dass die Perspektive und Größenabbildung ungefähr dem menschlichen Auge und der menschlichen Wahrnehmung entspricht. So wirken die Proportionen der Motive natürlich und gewohnt.

Objektive mit kürzerer Brennweite werden als Weitwinkelobjektive bezeichnet. Der Bildwinkel ist größer als bei einer Normalbrennweite. Bei gleichem Motivabstand wird mit einem Weitwinkelobjektiv mehr von dem Motiv aufgenommen als mit einem Normalobjektiv. Häufig werden Weitwinkelobjektive für Architektur- oder Landschaftsaufnahmen verwendet.

Objektive mit größeren Brennweiten werden als Teleobjektive bezeichnet. Der kleinere Bildwinkel dieser Objektive bietet die Möglichkeit, Motive schon aus der Ferne formatfüllend zu erfassen und die Konzentration darauf zu legen.

Es gibt sowohl variable Brennweiten (Zoomobjektive) als auch Festbrennweiten. Als Festbrennweite werden Objektive bezeichnet, die konstruktionsbedingt keine Änderung der Brennweite zulassen. Festbrennweiten können durch die einfachere Konstruktion eine höhere Abbildungsleistung und Lichtstärke aufweisen als Zoomobjektive, die wiederum flexibler einsetzbar sind.

Abbildungsfehler mit direktem Zusammenhang zur Brennweite

Die Brennweite ist streng genommen nur in der paraxialen Optik definiert. Jedoch ergeben sich unter bestimmten Bedingungen und vor allem für reale nichtparabolische Linsen diverse sog. Abbildungsfehler, die in einer (teilweise scheinbar) veränderten Brennweite resultieren.[4]

In der paraxialen Optik ist es immer möglich, eine Kugelfläche als Paraboloid anzunähern. Reale Linsen werden oft als Kugelflächen ausgeführt, da diese einfacher herzustellen sind als asphärische Flächen. Ihnen wird trotzdem eine Brennweite zugeordnet, die eigentlich nur für Strahlen nahe der optischen Achse gilt. Für achsfernere Strahlen ergeben sich verschobene Foki. Dieser Linsenfehler wird sphärische Aberration genannt.

Des Weiteren hängt die Brennweite unter anderem vom Brechungsindex des Linsenmaterials ab, der wiederum von der Wellenlänge des Lichts abhängt. Fällt nun Licht unterschiedlicher Wellenlänge (z. B. auch weißes Licht) auf eine Linse, so wird dieses wellenlängenabhängig auf verschiedene Punkte fokussiert. Man spricht von chromatischer Aberration.

Wenn die Form einer Linse nicht rotationssymmetrisch bzgl. der optischen Achse ist, sondern ellipsoid, dann fokussiert sie fächerartige Lichtbündel je nach deren Orientierung in verschiedenen Bildweiten. Volle Lichtbündel werden nicht auf einen Punkt fokussiert, sondern in zwei hintereinander liegende Brennlinien in den Richtungen der beiden Hauptachsen des Ellipsoids. Dieser Abbildungsfehler heißt axialer Astigmatismus.

Siehe auch

Schnittweite

Literatur

Max Born: Optik. 1972, ISBN 3-540-05954-7 (2. Kapitel).
Fritz Hodam: Technische Optik. 1967.
Wolfgang Demtröder: Elektrizität und Optik. Springer, Berlin 2006. ISBN 3-540-33794-6 (Kapitel 9.5)
Christian Westphalen: Die große Fotoschule – Handbuch digitale Fotopraxis. Rheinwerk Fotografie, ISBN 978-3-8362-7181-3 (Kapitel 2.1)

Weblinks

Wiktionary: Brennweite – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Einzelnachweise

Eugene Hecht: Optik. Oldenbourg Verlag, Kapitel 5 Geometrische Optik. Abschnitt 2 Linsen.
Brillenglas-Kompendium. (Memento vom 3. Juli 2013 im Webarchiv archive.today). Bei: Zeiss.de.
www.fotoschule.de
Wolfgang Demtröder: Elektrizität und Optik. Springer, Berlin 2006. ISBN 3-540-33794-6 (Kapitel 9.5.4).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Eugene Hecht: Optik. Oldenbourg Verlag, Kapitel 5 Geometrische Optik. Abschnitt 2 Linsen.

[2] Brillenglas-Kompendium. (Memento vom 3. Juli 2013 im Webarchiv archive.today). Bei: Zeiss.de.

[3] www.fotoschule.de

[4] Wolfgang Demtröder: Elektrizität und Optik. Springer, Berlin 2006. ISBN 3-540-33794-6 (Kapitel 9.5.4).