Gleitkommazahl

Eine Gleitkommazahl – häufig auch Fließkommazahl genannt (englisch floating point number oder kurz float, wörtlich Zahl mit flottierendem Punkt oder auch [wohl weiter lehnübersetzt] Gleitpunktzahl) – ist eine angenäherte Darstellung einer reellen Zahl.

Exakt darstellbare Gleitkommazahlen für verschiedene Mantissenlängen, Basis: 2, Exponent −3 bis 1

Die Menge der Gleitkommazahlen ist eine Teilmenge der rationalen Zahlen. Zusammen mit den auf ihnen definierten Operationen (Gleitkommaarithmetik) bilden die Gleitkommazahlen eine endliche Arithmetik, die vor allem im Hinblick auf numerische Berechnungen mit (binären) Rechnern entwickelt wurde.

Grundlagen

Problem

Alle (mechanischen oder elektronischen) Rechenhilfsmittel vom Abakus bis zum Computer verwenden als einfachste Form der Zahldarstellung Festkommazahlen. Dabei wird eine meistens begrenzte Ziffernfolge gespeichert und an festgelegter Stelle das Komma angenommen.

Bei größeren Rechnungen treten unweigerlich Überläufe auf, die eine Skalierung der Werte und eine erneute Durchrechnung erforderlich machen, um Endergebnis und alle Zwischenergebnisse in den erlaubten Wertebereich zu bringen. Diese Skalierung ist zeitraubend und muss automatisiert werden.

Exponentialschreibweise

Ein naheliegender und direkt zu Gleitkommazahlen führender Gedanke ist dabei, bei jedem Wert die genaue Stelle des Kommas zusätzlich zu speichern. Das bedeutet mathematisch nichts anderes als die Darstellung der Zahl $x$ mit zwei Werten, der Mantisse $m$ und dem Exponenten $e$ , so dass $x=m\cdot 10^{e}$ . Die Freiheit bei der Wahl des Exponenten kann genutzt werden, um die Mantisse in einen festgelegten Wertebereich, zum Beispiel $1\leq m<10$ zu bringen. Dieser Schritt heißt Normalisierung der Mantisse.

Beispiel: Der Wert der Lichtgeschwindigkeit beträgt

{\begin{aligned}c&=299\,792\,458\;{\text{m/s}}\\&=299\,792{,}458\cdot 10^{3}{\text{m/s}}\\&=0{,}299\,792\,458\cdot 10^{9}{\text{m/s}}\\&=2{,}997\,924\,58\cdot 10^{8}{\text{m/s}}\end{aligned}}

Nur die Mantisse der letzten Darstellung ist normalisiert.

Diese Schreibweise wird von Physikern und Mathematikern schon seit langem verwendet, um sehr große und sehr kleine Zahlen anzugeben. Noch heute wird deshalb die Gleitkommaschreibweise auf Taschenrechnern speziell als wissenschaftliches Format (sci) bezeichnet.

In Programmiersprachen wird für die Notation von Gleitkommazahlen im Quelltext und für ihre Ein- und Ausgabe eine kompakte Variante der Exponentialschreibweise verwendet, z. B. 2.99792458e8 (= 2,997.924.58 · 10⁸) oder 3.141592653589793d0 (d wird bei Zahlen in doppelter Genauigkeit benutzt). Das e bzw. d – ursprünglich die Großbuchstaben E und D – ist also als Kurzform von „mal 10 hoch“ zu verstehen. In der Sprache Algol 60 war dafür ein eigenes Zeichen ⏨ (Basiszehn) vorgesehen, das zwar auf manchen Ein- und Ausgabegeräten damaliger Rechner vorhanden war, aber erst 2002, also nach der Verwendungszeit von Algol 60, als Unicode-Zeichen U+23E8 in einen genormten Zeichencode aufgenommen wurde.

Gleitkommaarithmetik

Bei Rechnungen mit Gleitkommazahlen wird jede Zahl und jedes Zwischenergebnis individuell skaliert (im Gegensatz zu einer globalen Skalierung). Die Skalierung (Berechnung des Exponenten) jedes Zwischenergebnisses erfordert zusätzlichen Rechenaufwand und wurde deshalb bis weit in die 1980er Jahre nach Möglichkeit vermieden. So hatten die damaligen PCs standardmäßig keinen Gleitkommaprozessor. Ein weiterer Faktor war der höhere Speicherbedarf von Gleitkommazahlen, der nur durch Verzicht auf höhere Genauigkeit eingeschränkt werden konnte. Dementsprechend hatten zunächst nur die Höchstleistungsrechner (number cruncher) eine Gleitkommaarithmetik oder wenigstens eine Hardwareunterstützung einer Software-Gleitkommaarithmetik.

Die Wahl der Basis 10 ist willkürlich und nur dem üblichen Zehnersystem geschuldet. Gleitkommazahlen können mit beliebigen Basen dargestellt werden, im Allgemeinen gilt $x=m\cdot b^{e}$ mit einer beliebig gewählten Basis $b$ . Rechenanlagen verwenden $b=2$ (vorherrschend), $b=16$ (heute selten) oder $b=10$ (z. B. für Finanzmathematik, siehe unten). Bei beliebiger Basis ist die Bedingung für normalisierte Zahlen $1\leq m<b$ .

Geschichtliche Entwicklung

Die erste dokumentierte Verwendung der Gleitkommaschreibweise liegt etwa 2700 Jahre zurück: Im Zweistromland (Mesopotamien) wurden wissenschaftliche Rechnungen mit der Basis $b=60$ durchgeführt und der Exponent (eine meistens kleine ganze Zahl) einfach im Kopf mitgeführt.[1][2][3][4] Dasselbe Vorgehen war bis vor kurzer Zeit bei Berechnungen mit einem Rechenschieber üblich.

In Rechenautomaten wurde erstmals von Konrad Zuse eine eigene Gleitkommadarstellung für seine Computer Z1 und Z3 verwendet.

Darstellung

Im vorigen Abschnitt wurden die grundlegenden Parameter einer Gleitkommazahl bereits vorgestellt. Es sind Basis $b$ , Anzahl der Mantissenstellen $p$ und Anzahl der Exponentenstellen $r$ . Hinzu kommen weitere Parameter, die beim Rechnen die Rechenoperationen erleichtern sollen. In diesem Abschnitt werden Parameter und Bitfelder einer allgemeinen Gleitkommazahl kurz beschrieben.

Basis

$2{,}997.924.58\cdot {\color {red}10}^{8}$

Ein Parameter ist die gewählte Basis ${\boldsymbol {b}}$ . Zahlen, die von Menschen direkt verarbeitet werden, verwenden entweder $b=10$ oder $b=1000$ . In diesem speziellen Fall verwendet man für den Exponenten die Vorsätze Kilo=1000¹, Mega=1000², Giga=1000³, Tera=1000⁴ und Milli=1000⁻¹, Mikro=1000⁻², Nano=1000⁻³, Piko=1000⁻⁴ des internationalen Einheitensystems.

Im Computer haben sich das Dualsystem und seine Verwandten durchgesetzt und es sind die Basen $b=2$ , $b=8$ und $b=16$ üblich. Seit der Norm für Gleitkommazahlen IEEE 754 wird in modernen Computern fast ausschließlich die Basis $b=2$ verwendet.

Mantisse

${\color {red}2}{,}{\color {red}997}{.}{\color {red}924}{.}{\color {red}58}\cdot 10^{8}$

Die Mantisse ${\boldsymbol {m}}$ enthält die Ziffern der Gleitkommazahl. Speichert man mehr Ziffern ab, so erhöht sich die Genauigkeit. Die Anzahl $p$ der Mantissenziffern drückt also aus, wie exakt die Zahl approximiert wird. Dieser Gleitkommaparameter wird entweder direkt angegeben oder auch in Form der kleinsten Zahl $\epsilon$ beschrieben, die zu 1 addiert werden kann und ein von 1 verschiedenes Ergebnis liefert ( $1+\epsilon >1$ ; $\epsilon$ minimal!) (s. u. bei Eigenschaften).

Beispiel: Bei IEEE-754-Zahlen vom Typ Single mit der Basis $b=2$ ist die Mantisse $p=23$ Stellen lang. Hier ist $\epsilon =$ 1,19209289551e−0007.

Exponent

$2{,}997.924.58\cdot 10^{\color {red}8}$

Der Exponent ${\boldsymbol {e}}$ speichert nach Normalisierung die genaue Stelle des Kommas und damit die Größenordnung der Zahl. Die Anzahl $r$ der Exponentenziffern beschränkt die Variationsmöglichkeiten des Kommas und beschreibt damit den Wertebereich der dargestellten Gleitkommazahlen. Um ein System von Gleitkommazahlen zu beschreiben, gibt man den kleinsten und den größten möglichen Exponenten an oder auch die Anzahl der Exponenten und die Verschiebung zur 0 (Bias).

Beispiel: Bei IEEE-754-Zahlen vom Typ Single mit der Basis $b=2$ ist der kleinste mögliche Exponent −126 und der größte 127. Damit ist die größte in diesem System darstellbare Gleitkommazahl $\max =1{,}1111\ldots \cdot 2^{127}\approx 3{,}4\cdot 10^{+38}$ und die kleinste positive normalisierte Gleitkommazahl $\operatorname {minpos} =1{,}00000\ldots \cdot 2^{-126}\approx 1{,}175\cdot 10^{-38}$ . Diese Größen, $\max =3{,}4\cdot 10^{+38}$ und $\operatorname {minpos} =1{,}175\cdot 10^{-38}$ , beschreiben den zulässigen Wertebereich.

Normalisierung

${\color {red}2{,}}997.924.58\cdot 10^{8}$

Die Darstellung einer Gleitkommazahl ist zunächst nicht eindeutig bestimmt. Die Zahl 2 kann als $2{,}0\cdot 10^{0}$ oder auch $0{,}2\cdot 10^{1}$ geschrieben werden.

Um die Benutzung einer eindeutig bestimmten Darstellung zu erzwingen, werden daher oft normalisierte Gleitkommazahlen verwendet, bei denen die Mantisse in einen definierten Bereich gebracht wird. Zwei naheliegende Normalisierungsbedingungen sind $1/b\leq m<1$ und $1\leq m<b$ . Die Zahl 2 würde man also nach der ersten Regel als $0{,}2\cdot 10^{1}$ schreiben, die Darstellung $2{,}0\cdot 10^{0}$ wäre dann nicht erlaubt. Das Rechnen mit normalisierten Zahlen ist einfacher, weshalb in der Vergangenheit manche Implementatoren einer Gleitkommaarithmetik nur normalisierte Zahlen zuließen. Die Zahl 0 kann allerdings nicht normalisiert dargestellt werden.

Dabei unterscheidet man – in Bezug zur üblichen Basis 10 im Zahlensystem:

Wissenschaftliche Notation mit konsequenter Normalisierung auf $1\leq m<10$ $\text{[math]}$
- Beispiel: 10000 = 1e⁴
Technische Notation mit Normalisierung auf $1/f\leq m<1000$ $\text{[math]}$ , mit f als Potenz der Anzahl der verbleibenden signifikanten Stellen der Messunsicherheit für die Rechengenauigkeit (denormalisierte Stellen). Im Exponent erscheinen nur Vielfache von 3 – diese Darstellung lässt sich beim Rechnen mit Maßeinheiten sowohl zwanglos in die Einheitenvorsätze, als auch die Zifferngruppierung mit Tausendertrennzeichnung überführen, bzw. sich daraus erzeugen
- Beispiel: 10.000 m = 10e³ m = 10 km
- Signifikanz: 10.00e³ m = 10.000 ± 5 m (4 signifikante Stellen bezüglich Messung in Kilometern mit Rundung), aber 0.01e⁶ m = 10.000 ± 5000 m (2 signifikante Stellen bezüglich Messung in Mm) – wobei die präzisen Angaben über Standard- und erweiterte Messunsicherheit DIN 1319-3 bzw. dem ISO/BIPM-Guide (GUM, ENV 13005) folgen
IEEE 754 (Gleitkommazahlen für Mikroprozessoren) verwendet bei normalisierten Zahlen die Normalisierungsbedingung $1\leq m<2$ und erlaubt zwischen 0 und minpos zusätzlich denormalisierte (subnormale) Zahlen.

Darstellung des Exponentenvorzeichens mit oder ohne Bias

In Gleitkommasystemen ist der Exponent eine Zahl mit Vorzeichen. Das macht die Implementierung einer zusätzlichen ganzzahligen Arithmetik mit Vorzeichen für Exponentenberechnungen erforderlich. Dieser zusätzliche Aufwand kann vermieden werden, wenn zum Exponenten $e$ eine feste Zahl $B$ , der Biaswert oder Exzess, addiert wird und statt des Exponenten $e$ die Summe $E=e+B$ gespeichert wird. Diese Summe ist dann eine vorzeichenfreie positive Zahl. Meistens wird die Verwendung eines Bias $B$ mit der Darstellung der 0 durch $e=0$ kombiniert.

Eine heute selten anzutreffende Alternative ist die Darstellung des Exponenten im Zweierkomplement, im Einerkomplement oder als Betrags-Vorzeichenzahl.

Der Vorteil der Biased-Darstellung besteht darin, dass auf diese Weise ein Größenvergleich zwischen zwei positiven Gleitkommazahlen erleichtert wird. Es genügt, die Ziffernfolgen em, also jeweils Exponent e gefolgt von Mantisse m, lexikografisch miteinander zu vergleichen. Eine Gleitkomma-Subtraktion mit anschließendem Vergleich auf Null wäre weitaus aufwändiger. Der Nachteil der Biased-Darstellung gegenüber der Zweierkomplement-Darstellung besteht darin, dass nach einer Addition zweier Biased-Exponenten der Bias subtrahiert werden muss, um das richtige Ergebnis zu erhalten.

IEEE 754 verwendet die Darstellung mit B=127 bei Single und B=1023 bei Double.

Vorzeichen der Zahl

Das Vorzeichen v einer Gleitkommazahl (+ oder −; auch +1 oder −1) kann immer in einem Bit kodiert werden. Meistens wird das Bit $S=0$ für positive Zahlen (+) und das Bit $S=1$ für negative Zahlen (−) verwendet. Mathematisch kann man schreiben $v=(-1)^{S}$

Kurzdarstellung der Parameter

In den letzten Jahren hat sich die folgende Kurzdarstellung der wesentlichen Parameter $b$ , $p$ , $r$ und $B$ eines Gleitkommasystems durchgesetzt. Dabei schreibt man durch Punkte getrennt die Größen 1, $r$ , $p$ , $B$ und $b$ in genau dieser Reihenfolge auf. Die 1 ist dabei die Anzahl der Vorzeichenbits. Eine IEEE-754-Single-Zahl mit 1 Vorzeichenbit, 8 Exponentenbits und 23 Mantissenbits ist also eine 1.8.23.127.2 Gleitkommazahl. Geht die Basis $b$ und der Bias $B$ aus dem Zusammenhang hervor, kann beides weggelassen werden und man spricht von einer 1.8.23-Gleitkommazahl.

Eine zweite gängige Schreibweise lässt das Vorzeichenbit weg und gibt nur Mantissenlänge und Exponentenlänge an: s23e8.

Mit diesen Schreibweisen gilt für IEEE-754-Zahlen:

half:   1.5.10.15.2,       1.5.10          oder s10e5
single: 1.8.23.127.2,      1.8.23          oder s23e8
double: 1.11.52.1023.2,    1.11.52         oder s52e11
quad:   1.15.112.16383.2,  1.15.16383      oder s112e15
oct:    1.19.236.262143.2, 1.19.236.262143 oder s236e19

Hidden bit

Bei der Darstellung normalisierter Mantissen im Binärsystem kann ein Bit eingespart werden. Da die erste Stelle einer normalisierten Zahl immer ungleich 0 ist, ist diese Stelle im Binärsystem immer gleich 1. Eine Ziffer mit dem festen Wert 1 muss nicht mehr explizit gespeichert werden, da sie implizit bekannt ist. Wird diese Möglichkeit genutzt, wird von einem hidden bit (engl. wörtlich „verstecktes Bit“) gesprochen. Das erwähnte IEEE-Format für Gleitkommazahlen macht von dieser Einsparungsmöglichkeit Gebrauch, nicht jedoch das interne 80-Bit-Format der Intel-CPUs.

Soll beispielsweise die Zahl 5,25 nach IEEE 754 in ein short real (single precision number) umgewandelt werden, wird nach dem Zwischenschritt der Binärwandlung zu 101,01 das Komma zweimal linksseitig verschoben, sodass eine normierte binäre Darstellung mit 1,0101e2 gegeben ist. Aufgrund des hidden bit wird lediglich die Zahlenfolge 0101 in die 23-stellige Mantisse übernommen. Die Verwendung eines hidden bit erzwingt allerdings eine gesonderte Darstellung der Null, da jede Mantisse aufgrund des hidden bit einen Wert größer 0 repräsentiert.

Eigenschaften einer Gleitkommaarithmetik

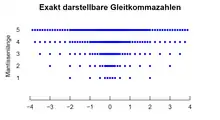
Gleitkommazahlen warten besonders für den mathematischen Laien mit einigen Überraschungen auf, die auch oft das Ergebnis von Taschenrechner- und Computerrechnungen beeinflussen. Am wichtigsten sind außer Kraft gesetzte geläufige mathematische Rechenregeln. Wer intensiv mit einem Rechenhilfsmittel arbeitet, muss diese Eigenschaften kennen. Sie gehen auf die begrenzte Genauigkeit zurück, mit der Mantisse und Exponent gespeichert werden. Die Konsequenz dieser Begrenzung wird klar, wenn man sich überlegt, dass die unendlich vielen reellen Zahlen durch endlich viele Ziffernkombinationen dargestellt werden sollen. Man kann sich die Gleitkommazahlen im Definitionsbereich eines Systems als lange Tabelle diskreter Werte vorstellen. Eine Gleitkommafunktion ordnet dann jedem Wert dieser Liste einen anderen Wert zu. Analoges gilt für zwei- und mehrstellige Operationen. Im Artikel Minifloats sind die entsprechenden Wertebereiche grafisch dargestellt.

Daraus resultiert die leichte bis absolute Ungenauigkeit der Rechnungen und die außer Kraft gesetzte Gültigkeit geläufiger mathematischer Rechenregeln.

Auslöschung

Unter Auslöschung versteht man den Effekt, dass bei der Subtraktion fast gleich großer Zahlen das Ergebnis falsch wird.

Beispiel:

Subtrahiert man $\pi =3{,}141592653589793\ldots$ und die Zahl 3,141 in einer vierstelligen Gleitkommaarithmetik ( $b=10$ , $p=4$ ), so erwartet der Laie als korrekt gerundetes Ergebnis $\pi -3{,}141=0{,}000592653589793\ldots \approx 5{,}927\ldots \cdot 10^{-4}$ .

Tatsächlich erhält man als Ergebnis $1{,}0000\cdot 10^{-3}$ : Der vierstellige gerundete Wert von $\pi =3{,}141592653589793\ldots$ ist $\pi =3{,}142\$ , damit wird das Ergebnis der Rechnung zu $3{,}142-3{,}141=0{,}001=1{,}0000\cdot 10^{-3}$ . Zu diesem Ergebnis kommt es, da schon die Ausgangsgrößen, insbesondere $\pi$ in der Gleitkommaarithmetik dargestellt sind und eben nicht exakt vorliegen.

Zahlen verschiedener Größenordnung (Absorption)

Die Addition bzw. Subtraktion einer betragsmäßig viel kleineren Zahl ändert die größere Zahl nicht.

Im Beispiel der vierstelligen Dezimalarithmetik ( $b=10$ , $p=4$ ) ändert die Addition von 0,001 zu 100 am größeren Operanden nichts. Dasselbe gilt für die Subtraktion:

$1{,}000\cdot 10^{2}+1{,}000\cdot 10^{-3}=1{,}000\cdot 10^{2}+0{,}000|01\cdot 10^{2}=1{,}000\cdot 10^{2}+0{,}000\cdot 10^{2}=1{,}000\cdot 10^{2}$

(Die Ziffern hinter dem Strich | entfallen bei der Skalierung)

Unterlauf

Da es in der Gleitkommadarstellung eine kleinste positive Zahl gibt, unterhalb derer kein Wert mehr dargestellt werden kann, wird ein Ergebnis in diesem Bereich meistens durch 0 repräsentiert. In diesem Fall spricht man von einem Unterlauf (engl. underflow). Handelt es sich um ein Zwischenergebnis, so ist an diesem Punkt jede Information über das Ergebnis verloren gegangen. In manchen Fällen wird die Genauigkeit des Endergebnisses davon nicht berührt, aber in anderen Fällen kann das resultierende Endergebnis auch komplett falsch sein.

Ungültigkeit der Assoziativ- und Distributivgesetze

Die Addition und die Multiplikation von Gleitkommazahlen sind nicht assoziativ, das heißt im Allgemeinen gilt:

$(x+y)+z\neq x+(y+z)$
$(x\cdot y)\cdot z\neq x\cdot (y\cdot z)$

Die Addition und Multiplikation von Gleitkommazahlen sind auch nicht distributiv, das heißt im Allgemeinen gilt:

$x\cdot (y+z)\neq (x\cdot y)+(x\cdot z)$
$(x+y)\cdot z\neq (x\cdot z)+(y\cdot z)$

Lösbarkeit von Gleichungen

In einer Gleitkommaarithmetik haben manche normalerweise unlösbare Gleichungen eine Lösung. Dieser Effekt wird sogar ausgenutzt, um ein solches Gleitkommasystem zu beschreiben.

Beispiel:

Im Bereich der reellen Zahlen hat die Gleichung $(1+x)=1$ für $x\neq 0$ keine Lösung.

In einer Gleitkommaarithmetik hat diese Gleichung viele Lösungen, nämlich alle Zahlen, die zu klein sind, um bei der Summe noch einen Effekt zu ergeben. Wieder mit dem Beispiel vierstelliger Dezimalbrüche ( $b=10$ , $p=4$ ) gilt (Der Strich | markiert die bei der Addition entfallenden Stellen):

1 + 1e−3 ,0= 1,000 + 0,001|000000… = 1,000 + 0,001 = 1,001 > 1
1 + 1e−4 ,0= 1,000 + 0,000|10000… 0= 1,000 + 0,000 = 1,000 = 1
1 + 2,3e−5 = 1,000 + 0,000|023000… = 1,000 + 0,000 = 1,000 = 1

Die schon oben erwähnte kleinste Zahl $\epsilon$ , die zu 1 addiert werden kann und ein von 1 verschiedenes Ergebnis liefert ( $1+\epsilon >1$ ; $\epsilon$ minimal!) nennt man Maschinengenauigkeit.

Konversionen

Wenn die Basis verschieden von 10 ist, müssen die Zahlen zwischen dem vorliegenden Gleitkommasystem und dem Dezimalsystem konvertiert werden, um eine menschenlesbare Darstellung zu erhalten. Das wird meist schnell (und oft ungenau) programmiert. Eine schon alte und wichtige Forderung an diese Konversion ist ihre bitgenaue Umkehrbarkeit. Ein im Dezimalsystem dargestelltes Ergebnis soll wieder eingelesen werden können und bitgenau dieselbe Darstellung im Gleitkommasystem reproduzieren.

Diese Forderung wird häufig nicht beachtet. Eine Ausnahme ist hier Java, das den folgenden Satz beachtet:

Satz: Man kann zeigen, dass es nicht ausreicht, die aufgrund der Mantissengenauigkeit berechnete Anzahl der Dezimalstellen aufzurunden und diese Dezimalstellen gerundet zu produzieren. Eine einzige weitere Stelle reicht jedoch aus (Theorem 15[5]). Das ist der Grund, warum in der Darstellung reeller Zahlen, die von Java-Programmen produziert werden, immer eine zusätzliche und scheinbar überflüssige Stelle erscheint.

Dezimalbrüche

Schon einfache Dezimalbrüche wie 0,1 können nicht exakt als binäre Gleitkommazahlen dargestellt werden, da jede rationale Zahl, deren gekürzter Nenner keine Zweierpotenz ist, im Binärsystem zu einer nicht abbrechenden, periodischen Darstellung führt. Von dieser werden nur die ersten $p$ Ziffern gespeichert, wodurch Ungenauigkeit entsteht. Dezimal 0,1 ist binär 0,0001100110011… Allerdings wurde für binäre Gleitkommasysteme mit entsprechenden Rundungsregeln bewiesen, dass die Darstellung von 0,1 multipliziert mit 10 wieder exakt 1 ergibt. Allgemein gilt bei richtiger Rundung (m / 10) · 10 = m (Goldbergs Theorem 7[5] für den konkreten Fall n = 2¹ + 2³ = 10).

In Disziplinen wie der Finanzmathematik werden oft Ergebnisse verlangt, die mit einer Handrechnung exakt übereinstimmen. Das geht nur mit einer dezimalen Gleitkommaarithmetik[6] oder – mit einigen „Verrenkungen“ – mit einer Festkommaarithmetik.

Prüfung auf Gleichheit

Die im Abschnitt Dezimalbrüche genannte Einschränkung, dass viele dieser Dezimalzahlen im Binärsystem eines Computers nicht genau dargestellt werden können, hat beim Programmieren Auswirkungen auf Vergleiche $x=y$ zwischen Gleitkommazahlen. Ein Beispiel in der Programmiersprache C soll dies verdeutlichen:

#include <stdio.h>
int main(void) {
 if (0.362 * 100.0 != 36.2)
  puts("verschieden");

 if (0.362 * 100.0 / 100.0 != 0.362)
  puts("auch verschieden");
 return 0;
}

Obwohl die beiden Gleichungen $0{,}362\cdot 100=36{,}2$ und $0{,}362\cdot 100/100=0{,}362$ mathematisch korrekt sind, werden sie wegen der ungenauen Umrechnung ins Computer-Binärsystem falsch. Im Beispiel-Programm werden somit beide Ungleichungen als wahr angesehen.

Vergleiche müssen deshalb durch eine Abfrage ersetzt werden, ob die zu vergleichenden Werte im Rahmen einer erreichbaren Genauigkeit $\varepsilon$ (meist Toleranz genannt) als gleich angesehen werden können.

Toleriert man beim Vergleich einen absoluten Fehler, lautet eine mögliche Formulierung $\vert x-y\vert \leq \varepsilon$ .

Toleriert man beim Vergleich einen relativen Fehler, lautet eine mögliche Formulierung $\vert 1-{\tfrac {y}{x}}\vert \leq \varepsilon$ . Der zweite Fall muss meist noch mit der Sonderfallabfrage $x\neq 0$ verbunden werden.

Alternativ kann man alle Faktoren respektive Summanden inklusive des zu erwartenden Ergebnisses eben jener problematischen Vergleiche bei rationalen Gleitkommazahlen $n_{1}n_{2}\dots n_{m}$ auch mit $10^{\left(n_{m}\right)}$ multiplizieren, wobei $m$ den Index der letzten Nachkommastelle angibt. Allgemeiner gesagt: Alle Gleitkommazahlen müssen – sofern möglich – in Brüche umgewandelt werden. Diese können wiederum eindeutig und ohne Rundungen der Mantisse in das binäre Zahlensystem konvertiert werden. Compiler mancher Programmiersprachen (z. B. Java, Ruby, C++, Objective-C, Swift, Rust usw.) können direkt mit den Brüchen rechnen und vergleichen die Brüche in den oben aufgeführten bedingten Anweisungen (If-Anweisungen), welche dadurch nicht betreten werden. Andere Programmiersprachen (z. B. Object Pascal, PHP, JavaScript, Perl, Python usw.) wiederum wandeln den Bruch bzw. den Quotient als allerersten Schritt wieder in eine Binärzahl um und vergleichen dann erst beide Werte, wodurch in dem Fall beide Bedingungen wahr sind und die oben angegebenen Ausgaben getätigt werden.

Sogar Zahlen mit exakt denselben Bitmustern und somit eigentlich exakt identischen Werten werden vom Rechner mit $x=y$ manchmal nicht als gleich angesehen. Das hat als Ursache die manchmal nicht identischen Formate im Speicher (Bsp.: Intel 64 Bit) und während einer Rechnung in der Gleitpunkteinheit (Bsp.: Intel 80 Bit). Wenn dieselben Bitmuster, die verglichen werden sollen, einmal aus dem Speicher und somit gerundet und einmal aus der FPU und somit mit der vollen Genauigkeit kommen, führt ein Vergleich zum falschen Ergebnis. Die Abhilfe ist dieselbe wie schon beschrieben. Bei größer/kleiner Vergleichen kann dieses Problem auch auftauchen, je nach verwendeter Sprache und Architektur sind spezielle Befehle und/oder ein Umweg über den Arbeitsspeicher zu nehmen um dies zu lösen.

Versteckte Verwendung anderer Darstellungen

Manche Rechenanlagen verwenden beim Rechnen mehrere verschiedene Formate. Bei Intel und verwandten Prozessoren wie AMD rechnet die FPU mit einem 80-Bit-Format. Gespeichert werden die Zahlen mit einem IEEE-754-kompatiblen 64-Bit- bzw. 32-Bit-Format. Bei Verwendung von MMX/SSE-Erweiterungen werden wieder andere Rechenformate verwendet. Das führt zu weiteren für Laien zunächst sehr undurchsichtigen Eigenschaften. Ein simpler Vergleich identischer Bitmuster auf Gleichheit kann zum Ergebnis führen, dass die scheinbar identischen Bitmuster doch verschieden sind. Das folgende Programm liefert manchmal paradoxe Ergebnisse, wenn man es mit dem gleichen Wert für x und y aufruft:

void vergleiche (double x, double y) {
 if(x != cos (y))
  printf("paradox\n");
 else
  printf("wuerde jeder so erwarten\n");
}
...
double z = 0.2; // der Wert ist nicht wichtig
vergleiche (cos (z), z);

 mit dem Ergebnis:  paradox

Die Erklärung für dieses Verhalten ist, dass der Compiler zwei unabhängige cos-Berechnungen generiert, die eine vor dem Aufruf von vergleiche, die andere in vergleiche. Die Variable x empfängt den cos(z) mit 64 Bit. Die Berechnung des cos(y) kann bei Intel mit 80 Bit erfolgen; die beiden Ergebnisse sind unterschiedlich, wenn cos(y) nicht im Speicher, sondern direkt vom 80-bittigen Arbeitsregister mit der 64-bittigen Variablen x verglichen wird.

Binärgleitkommazahlen in der Digitaltechnik

Oben erwähnte Beispiele sind durchwegs im Dezimalsystem angegeben, das heißt mit einer Basis b = 10. Computer verwenden stattdessen das Binärsystem mit einer Basis b = 2.

Einfache und doppelte Genauigkeit

Gleitkommazahlen werden in Computern normalerweise als Folgen von 32 Bit (einfache Genauigkeit, englisch single precision) oder 64 Bit (doppelte Genauigkeit, double precision) dargestellt.

Manche Prozessoren erlauben auch längere Gleitkommazahlen, so kennen die von der Intel-x86-Serie abgeleiteten Prozessoren (u. a. Intel Pentium und AMD Athlon) eine Gleitkommazahldarstellung mit 80 Bit für Zwischenergebnisse. Manche Systeme erlauben auch Gleitkommazahlen mit 128 Bit (Vierfache Genauigkeit). Einige ältere Systeme verwendeten auch noch andere Längen wie zum Beispiel 36 Bit (IBM 704, PDP-10, UNIVAC 1100/2200 series), 48 Bit (Burroughs) oder 60 Bit (CDC 6600),

Daneben gibt es auch Minifloats genannte Systeme mit sehr wenigen Bits (etwa 8 oder 16), die in speicherarmen Systemen (Controllern) oder limitierten Datenströmen eingesetzt werden (zum Beispiel Grafikkarten).

IEEE 754 und andere Normen

Das heute häufigste und bekannteste Gleitkommasystem wurde 1985 von IEEE konzipiert, in der IEEE 754 niedergelegt, und ist in den meisten Computern als Hardware- oder Softwarearithmetik vorhanden. IEEE 854 ist eine Norm für Gleitkomma-Dezimalzahlen oder Dezimalbrüche. Beide Normen werden in der Revision IEEE 754r zusammengeführt und erweitert.

Die IEEE hat die Darstellung von Gleitkommazahlen in ihrem Standard IEEE 754 seit 1985 reglementiert; beinahe alle modernen Prozessoren folgen diesem Standard. Gegenbeispiele, die die Spezifikationen der Norm IEEE 754 nicht erfüllen, sind einige IBM-Großrechnersysteme (Hexfloat-Format), die VAX-Architektur und einige Supercomputer wie die von Cray. Die Sprache Java lehnt sich eng an IEEE 754 an, erfüllt die Norm aber nicht komplett.

Die Definition des Hexfloat-Formates von IBM findet sich im Buch „Principles of Operation“ der z-Architektur.[7]

Der Power6 von IBM ist einer der ersten Prozessoren, welche dezimale Gleitkommaarithmetik hardwaremäßig implementiert haben; die Basis ist also 10. Im Folgenden wird aber nur die Basis 2 behandelt.

Strenggenommen sind nur die normalisierten Zahlen aus IEEE 754 Gleitkommazahlen. Die denormalisierten Zahlen sind eigentlich Festkommazahlen; diese Sonderfälle wurden für spezielle numerische Zwecke geschaffen.

Interne Darstellung

Die tatsächliche Darstellung im Computer besteht also aus einem Vorzeichen-Bit, einigen Exponenten-Bits und einigen Mantissen-Bits. Wobei die Mantisse meistens normiert ist und Zahlen im Intervall [1; 2[ darstellt. (Da in diesem Intervall das erste Bit mit der Wertigkeit Eins stets gesetzt ist, wird es meistens implizit angenommen und nicht gespeichert, siehe Hidden Bit). Der Exponent wird meistens im Biased-Format, oder auch im Zweierkomplement dargestellt. Des Weiteren werden zur Darstellung besonderer Werte (Null, Unendlich, Keine Zahl) meistens einige Exponentenwerte, zum Beispiel der größtmögliche und der kleinstmögliche Exponent, reserviert.

Eine Zahl f wird demzufolge als f = s · m · 2^e dargestellt, wobei s 1 oder −1 ist.

	IEEE 754		S/390
	Mantisse (in Bit)	Exponent (in Bit)	Mantisse (in Bit)	Exponent (in Bit)
Half	10	5
Single	23	8	24	7
Double	52	11	56	7
Extended	nicht exakt definiert		112	7

Einschränkungen und deren mathematische Grundlagen

Durch die unterschiedliche binäre Darstellung der Zahlen kann es in beiden Systemen zu Artefakten kommen. Das heißt: Rationale Zahlen, die im Dezimalsystem „rund“ erscheinen, zum Beispiel $\textstyle {\frac {249}{20}}=12{,}45$ , können im Binärsystem nicht exakt dargestellt werden (der Wert ist $1100{,}01{\overline {1100}}_{2}$ ). Stattdessen wird ihre Binärdarstellung im Rahmen der jeweiligen Rechengenauigkeit gerundet, so dass man bei der Rückumwandlung ins Dezimalsystem z. B. den Wert 12,44999999900468785 erhält. Dieses kann in nachfolgenden Berechnungen zu unvorhergesehenen Ab- oder Aufrundungsfehlern führen.

Die oben erwähnten Artefakte sind im Binärsystem unvermeidlich, da unendlich viele Zahlen, die im Dezimalsystem exakt dargestellt werden können, im Binärsystem periodische Zahlen mit unendlich vielen Nachkommastellen sind.[Anmerkung 1] Sie könnten nur durch die Verwendung von Codierungen mit der Basis 10 (oder anderer Basen der Form $10\cdot n$ mit beliebigem $n\in \mathbb {N}$ ) vermieden werden, siehe auch BCD-Code. Binäre Gleitkommazahlen werden jedoch nach wie vor aus verschiedenen Gründen eingesetzt.

Allgemein gibt es für jede Basis d unendlich viele rationale Zahlen, die zu einer anderen Basis eine endliche Darstellung (0-Periode) haben und zur Basis d eine unendliche Darstellung mit Periode. Das Dezimalsystem ist hier nur dadurch ausgezeichnet, dass Menschen daran gewöhnt sind, und daher für Eingabe- und Ausgabeformat der Rechnungen oft das Dezimalsystem bevorzugt wird.

In der Mathematik ist ein Gleitkommazahlensystem ein Tupel $\left(d,[e_{\mathrm {min} },e_{\mathrm {max} }],l\right)$ , wobei $d$ die Basis, $\left[e_{\mathrm {min} },e_{\mathrm {max} }\right]$ den Bereich des Exponenten und $l$ die Länge der Mantisse darstellt.

Damit ist eine reelle Zahl x ≠ 0 darstellbar durch ein a und ein e, so dass: $a=\sum _{i=1}^{l}a_{i}\cdot d^{-i}$ und $x=ad^{e}$ mit $e\in \left[e_{\mathrm {min} },e_{\mathrm {max} }\right]$ .

Hiermit ist eine mathematische Betrachtung des Rundungsfehlers möglich. Die obige Darstellung realisiert eine Projektion

fl\colon \mathbb {R} \to \{x\in \mathbb {R} \mid \exists a,e\colon x=ad^{e}\}

und damit ist der Rundungsfehler definiert als

{\displaystyle {\frac {|x-fl(x)|}{|x|}}\leq \varepsilon

Bei double-Werten entspricht $\varepsilon$ gerade $2^{-53}$ (ungefähr $1{,}1\cdot 10^{-16}$ ).

Beispiel: Berechnung Gleitkommazahl

18,4₁₀ soll in eine Gleitkommazahl umgewandelt werden, dabei nutzen wir den Single IEEE-Standard (IEEE 754, binary32).

1. Berechnung des Exzesses

(Der Exzess oder auch Bias ist eine zum Zahlenstandard gehörende Konstante. Hierfür zählen die Bits, die in der Zahlendarstellung für den Exponenten reserviert sind, bei der Norm IEEE 754 also 8 Stellen.)

Exzess = 2^(n-1) - 1
           (n Bits des Exponenten in der Zahlendarstellung)
       = 2^(8-1) - 1
       = (2⁷) - 1
       = 128 - 1
       = 127

2. Umwandlung eines Dezimalbruches in eine duale Festkommazahl ohne Vorzeichen

Gleitkommazahl = 18,4

Vorkommaanteil = 18
 18 / 2 = 9 Rest 0 (Least-Significant Bit)
  9 / 2 = 4 Rest 1
  4 / 2 = 2 Rest 0
  2 / 2 = 1 Rest 0
  1 / 2 = 0 Rest 1 (Most-Significant-Bit)
   = 10010

Nachkommaanteil = 0.4
 0,4 * 2 = 0,8 → 0 (Most-Significant-Bit)
 0,8 * 2 = 1,6 → 1
 0,6 * 2 = 1,2 → 1
 0,2 * 2 = 0,4 → 0
 0,4 * 2 = 0,8 → 0
 0,8 * 2 = 1,6 → 1 (Least-Significant-Bit)
    •
    •
    •
     = 0,0110011001100110011...

18,4 = 10010,011001100110011...

3. Normieren

10010,01100110011... * 2^0 = 1,001001100110011... * 2^4

4. Berechnung des dualen Exponenten

da 2^4 → Exponent = 4
Exponent + Exzess
   4 + 127 = 131

131/2 = 65 Rest 1 (Least-Significant-Bit)
 65/2 = 32 Rest 1
 32/2 = 16 Rest 0
 16/2 = 8  Rest 0
  8/2 = 4  Rest 0
  4/2 = 2  Rest 0
  2/2 = 1  Rest 0
  1/2 = 0  Rest 1 (Most-Significant-Bit)
   = 10000011

5. Vorzeichen-Bit bestimmen

Das Vorzeichen errechnet sich aus der Formel (-1)^s:

 positiv → 0
 negativ → 1
   = 0

6. Die Gleitkommazahl bilden

1 Bit Vorzeichen + 8 Bit Exponent + 23 Bit Mantisse
0 10000011 00100110011001100110011
  → die Vorkomma-Eins wird als Hidden Bit weggelassen;
    da dort immer eine 1 steht,
    braucht man diese nicht zu speichern

Berechnung einer IEEE single precision Gleitkommazahl (32-Bit-Gleitkommazahl)

Hier werden die genauen Rechenschritte vorgestellt, um einen Dezimalbruch in eine binäre Gleitkommazahl vom Typ Single nach IEEE 754 umzuwandeln. Dazu müssen nacheinander die drei Werte (Vorzeichen $v$ (1 bit), Mantisse $m$ und Exponent $e$ ) berechnet werden, aus denen sich die Zahl $x$ zusammensetzt:

$x=(-1)^{v}\cdot m\cdot 2^{e}$

Vorzeichen

Je nachdem, ob die Zahl positiv oder negativ ist, ist $v$ 0 oder 1: $(-1)^{0}=1$ oder $(-1)^{1}=-1$

Alle weiteren Berechnungen erfolgen mit dem Betrag der Zahl.

Exponent

Als Nächstes wird der Exponent gespeichert. Beim IEEE single-Datentyp sind dafür 8 Bit vorgesehen. Der Exponent muss so gewählt werden, dass die Mantisse einen Wert zwischen 1 und 2 erhält:

$e=\left\lfloor \log _{2}(|x|)\right\rfloor$

Wenn hierbei ein Wert für den Exponenten herauskommt, der kleiner −126 oder größer 127 ist, kann die Zahl mit diesem Datentyp nicht gespeichert werden. Stattdessen wird die Zahl als 0 (Null) oder als „unendlich“ abgespeichert.

Der Wert für den Exponenten wird jedoch nicht direkt gespeichert, sondern um einen Bias-Wert erhöht, um negative Werte zu vermeiden. Bei IEEE single ist der Bias-Wert 127. Somit werden die Exponentenwerte −126…+127 als sogenannte „Charakteristik“ zwischen 1…254 gespeichert. Die Werte 0 und 255 als Charakteristik sind reserviert für die speziellen Zahlenwerte „Null“, „Unendlich“ und „NaN“.

Mantisse

Die Mantisse wird nun in den verbleibenden 23 Bit abgespeichert:

$m=\left({\frac {|x|}{2^{e}}}-1\right)\cdot 2^{23}$

Zahlenbeispiel mit der Zahl 11,25

Zahl = +11,25

Vorzeichen = + → 0_binär

${\text{Exponent}}=\left\lfloor \log _{2}(11{,}25)\right\rfloor =\left\lfloor 3{,}49\right\rfloor =3$ → 3 + 127 = 130 → 10000010_binär

${\text{Mantisse}}=\left({\frac {11{,}25}{2^{3}}}-1\right)\cdot 2^{23}=(1{,}40625-1)\cdot 2^{23}=3407872$ → 01101000000000000000000_binär

Damit ergibt sich folgende Gleitkommazahl einfacher Genauigkeit:

0 10000010 01101000000000000000000

Umkehrung

Will man aus einer Gleitkommazahl im Maschinenwort (32 Bit) eine Dezimalzahl errechnen, so kann man dies mit folgender Formel recht schnell erledigen:

$Z=(-1)^{VZ}\cdot (1{,}0+M/2^{23})\cdot 2^{E-127}$

Berechnung einer IEEE double precision Gleitkommazahl (64-Bit-Gleitkommazahl)

Umkehrung:

Um aus einer Gleitkommazahl im Maschinenwort (64 Bit) eine Dezimalzahl zu errechnen, kann man die folgende Formel verwenden:

$Z=(-1)^{VZ}\cdot (1{,}0+M/2^{52})\cdot 2^{E-1023}$

Beispiel:

Folgende Binärzahl mit 64-Bit soll als Gleitkommazahl interpretiert werden:

0 10001110100 0000101001000111101011101111111011000101001101001001

(das Bit ganz links ist Bit 63 und das Bit ganz rechts ist Bit 0)

Bit 63 repräsentiert das Vorzeichen (1 Bit), also

  VZ = 0_binär = 0

Bit 62 bis 52 repräsentieren den Exponenten (11 Bit), also:

 E = 10001110100_binär = 1140

Bit 51 bis 0 repräsentieren die Mantisse (52 Bit), also:

  M = 0000101001000111101011101111111011000101001101001001_binär =  $180847918207817$

Eingesetzt in die Formel ergibt sich als Ergebnis (Rundungswerte):

  $Z=(-1)^{0}\cdot (1{,}0+180847918207817/2^{52})\cdot 2^{1140-1023}=1\cdot (1{,}040156304549969)\cdot 2^{117}=1{,}7282561\cdot 10^{35}$

Anmerkungen

Nämlich alle rationalen Zahlen, die sich mit einer Zehnerpotenz als Nenner darstellen lassen, aber nicht mit einer Zweierpotenz.

Siehe auch

Weblinks

Wiktionary: Fließkommazahl – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wiktionary: Gleitkommazahl – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wikibooks: ${\color {BlueViolet}{\begin{smallmatrix}{\mathbf {MATHE} \mu \alpha T\mathbb {R} ix}\end{smallmatrix}}}$ Mathematik für die Schule – Vorsilben und Gleitkommadarstellung

Binärformate reeller Zahlen (PDF; 192 kB)
Robert Munafo: Survey of Floating-Point Formats – Übersicht über historische Gleitkommaformate (englisch)
Chris Hecker: Let’s Get to the (Floating) Point – Kommen wir auf den (Gleit)punkt (PDF; englisch)
David Goldberg: What Every Computer Scientist Should Know About Floating-Point Arithmetic. (englisch)
David Monniaux: The pitfalls of verifying floating-point computations (englisch)
Gleitkommazahlen / Binäre Zahlen in der Informatik (relativ vereinfachte Darstellung)
Ein Applet zum Üben (benötigt Java)
Online Binary-Decimal Converter (englisch)

Einzelnachweise

Otto Neugebauer: The exact sciences in antiquity. Princeton University Press, 1952.
Bartel Leendert van der Waerden: Science awakening. P. Noordhoff, Groningen, 1954.
Donald E. Knuth: Ancient Babylonian algorithms. In: Commun. ACM. 15, 1972, S. 671–677, Korr. in Commun. ACM. 19, 1976, S. 108.
Donald E. Knuth: The Art of Computer Programming. Vol. 2: Seminumerical Algorithms. 3. Auflage. Addison-Wesley, 1997, S. 196.
David Goldberg: What Every Computer Scientist Should Know About Floating-Point Arithmetic. In: ACM Computing Surveys. Band 23, 1991, S. 5–48, doi:10.1145/103162.103163 (sun.com [abgerufen am 2. September 2010]).
General Decimal Arithmetic. IBM Corporation
Principles of Operation. (PDF; 4,7 MB) 2. Auflage. IBM Corporation, 2001, Kapitel 19-4

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[8] Nämlich alle rationalen Zahlen, die sich mit einer Zehnerpotenz als Nenner darstellen lassen, aber nicht mit einer Zweierpotenz.

[1] Otto Neugebauer: The exact sciences in antiquity. Princeton University Press, 1952.

[2] Bartel Leendert van der Waerden: Science awakening. P. Noordhoff, Groningen, 1954.

[3] Donald E. Knuth: Ancient Babylonian algorithms. In: Commun. ACM. 15, 1972, S. 671–677, Korr. in Commun. ACM. 19, 1976, S. 108.

[4] Donald E. Knuth: The Art of Computer Programming. Vol. 2: Seminumerical Algorithms. 3. Auflage. Addison-Wesley, 1997, S. 196.

[goldberg-5] David Goldberg: What Every Computer Scientist Should Know About Floating-Point Arithmetic. In: ACM Computing Surveys. Band 23, 1991, S. 5–48, doi:10.1145/103162.103163 (sun.com [abgerufen am 2. September 2010]).

[6] General Decimal Arithmetic. IBM Corporation

[7] Principles of Operation. (PDF; 4,7 MB) 2. Auflage. IBM Corporation, 2001, Kapitel 19-4