Grafikpipeline

Eine Computergrafik-Pipeline, auch Rendering-Pipeline oder einfach Grafikpipeline, ist eine Modellvorstellung in der Computergrafik, die beschreibt, welche Schritte ein Grafiksystem zum Rendern, also zur Darstellung einer 3D-Szene auf einem Bildschirm, durchführen muss. Da diese Schritte sowohl von der Soft- und Hardware als auch von den gewünschten Darstellungseigenschaften abhängen, gibt es keine allgemein gültige Grafikpipeline. Zur Ansteuerung von Grafikpipelines werden üblicherweise Grafik-APIs wie Direct3D oder OpenGL verwendet, die die zugrundeliegende Hardware abstrahieren und dem Programmierer viele Aufgaben abnehmen.

Die Darstellung dreidimensionaler Welten am Computer ist heute weit verbreitet und Teil sehr vieler Computerspiele. Das sogenannte Rendering erzeugt dabei aus abstrakten Daten Grafiken.

Das Modell der Grafikpipeline findet üblicherweise beim Echtzeitrendern Anwendung. Oft sind hier die meisten Schritte der Pipeline in Hardware implementiert, was besondere Optimierungen ermöglicht. Die Bezeichnung „Pipeline“ wird in einem ähnlichen Sinn wie die Pipeline bei Prozessoren verwendet: Die einzelnen Schritte der Pipeline laufen zwar parallel ab, sind jedoch solange blockiert, bis der langsamste Schritt beendet wurde.

Aufbau

Eine Grafikpipeline lässt sich in drei große Schritte aufteilen: Anwendung, Geometrie und Rasterung.[1]

Anwendung

Der Anwendungsschritt wird von der Software ausgeführt, er lässt sich daher nicht in pipelineartig ausgeführte Einzelschritte aufteilen. Es ist jedoch möglich, ihn auf Mehrkernprozessoren oder Mehrprozessorsystemen zu parallelisieren. Im Anwendungsschritt werden Änderungen an der Szene vorgenommen, wie sie zum Beispiel aufgrund der Benutzerinteraktion mittels Eingabegeräten oder bei einer Animation nötig sind. Die neue Szene mit allen ihren Primitiven – meist Dreiecke, Linien und Punkte – wird dann an den nächsten Schritt der Pipeline weitergeleitet.

Beispiele für Aufgaben, die typischerweise vom Anwendungsschritt übernommen werden, sind Kollisionserkennung, Animation, Morphing und die Datenverwaltung. Zu letzterer gehören etwa Beschleunigungstechniken mittels räumlicher Unterteilungsschemata (Quadtree, Octree), mit denen die aktuell im Speicher gehaltenen Daten optimiert werden. Die „Welt“ und ihre Texturen eines heutigen Computerspiels sind sehr viel größer als auf einmal in den verfügbaren Arbeitsspeicher oder Grafikspeicher geladen werden könnte.

Geometrie

Der Geometrieschritt, der für den Großteil der Operationen mit Polygonen und deren Eckpunkten (Vertices) verantwortlich ist, lässt sich in folgende fünf Aufgaben unterteilen. Es hängt von der jeweiligen Implementierung ab, wie diese Aufgaben als tatsächliche, parallel ausgeführte Pipeline-Schritte organisiert werden.

Definitionen

Ein Vertex (Mehrzahl: Vertices) ist ein Punkt in der Welt. Diese Punkte dienen dazu, die Flächen zu verbinden. In speziellen Fällen werden auch direkt Punktwolken gezeichnet, dies ist aber noch die Ausnahme.

Ein Dreieck (englisch: Triangle) ist das am häufigsten vorkommende geometrische Primitiv der Computergrafik. Es wird durch seine drei Ecken und einen Normalvektor definiert – letzterer dient dazu, die Vorderseite des Dreiecks anzugeben und ist ein Vektor, der senkrecht auf der Fläche steht. Ein solches Dreieck kann mit einer Farbe versehen sein oder mit einer Textur.

Das Weltkoordinatensystem

Das Weltkoordinatensystem ist das Koordinatensystem, in dem die virtuelle Welt angelegt wird. Dieses sollte, damit die nachfolgende Mathematik einfach anwendbar ist, einige Bedingungen erfüllen: Es muss sich um ein rechtwinkliges kartesisches Koordinatensystem handeln, bei dem alle Achsen gleich skaliert sind. Wie die Einheit des Koordinatensystems festgelegt wird, ist hingegen dem Entwickler überlassen. Ob also der Einheitsvektor des Systems in Wirklichkeit einem Meter oder einem Ångström entsprechen soll, ist vom Anwendungsfall abhängig. Ob ein rechtshändiges oder ein Linkshändiges Koordinatensystem verwendet werden soll, kann durch die zu verwendende Grafikbibliothek vorgegeben sein.

Beispiel: Wenn wir einen Flugsimulator entwickeln wollen, können wir das Weltkoordinatensystem so wählen, dass der Ursprung in der Mitte der Erde liegt und die Einheit auf einen Meter festlegen. Zusätzlich definieren wir – damit der Bezug zur Realität einfacher wird – dass die X-Achse den Äquator auf dem Nullmeridian schneiden soll und die Z-Achse durch die Pole verläuft. In einem Rechtssystem läuft damit die Y-Achse durch den 90°-Ost-Meridian (irgendwo im indischen Ozean). Jetzt haben wir ein Koordinatensystem, das jeden Punkt auf der Erde in kartesischen Koordinaten beschreibt. In diesem Koordinatensystem modellieren wir nun die Grundzüge unserer Welt, also Berge, Täler und Gewässer.

Anmerkung: Außerhalb der Computergeometrie verwendet man für die Erde geografische Koordinaten, also Längen- und Breitengrade, sowie Höhen über dem Meeresspiegel. Die näherungsweise Umrechnung – wenn man davon absieht, dass die Erde keine exakte Kugel ist – ist einfach:

{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}(R+{hasl})*\cos({lat})*\cos({long})\\(R+{hasl})*\cos({lat})*\sin({long})\\(R+{hasl})*\sin({lat})\end{pmatrix}}

mit R=Erdradius [6.378.137m], lat=Breitengrad, long=Längengrad, hasl=Höhe über Meer.

Sämtliche der folgenden Beispiele gelten in einem Rechtssystem. Für ein Linkssystem müssen eventuell Vorzeichen vertauscht werden.

Die in der Szene angegebenen Objekte (Häuser, Bäume, Autos) sind aus Gründen der einfacheren Modellierung oftmals in ihrem eigenen Objektkoordinatensystem (auch Modellkoordinatensystem oder lokales Koordinatensystem) angegeben. Um diesen Objekten Koordinaten im Weltkoordinatensystem oder globalen Koordinatensystem der gesamten Szene zuzuweisen, werden die Objektkoordinaten mittels Translation, Rotation oder Skalierung transformiert. Dies geschieht durch Multiplikationen der entsprechenden Transformationsmatrizen. Außerdem können aus einem Objekt mehrere unterschiedlich transformierte Kopien gebildet werden, etwa ein Wald aus einem Baum; diese Technik wird Instancing genannt.

Um ein Modell von einem Flugzeug in der Welt zu platzieren, bestimmen wir zunächst mal vier Matrizen. Da wir im dreidimensionalen Raum arbeiten, sind die homogenen Matrizen, die wir für unsere Berechnung brauchen, vierdimensional. Als erstes brauchen wir drei Rotationsmatrizen, nämlich für jede der drei Flugzeugachsen (Hochachse, Querachse, Längsachse) eine.

Um die X-Achse (im Objektkoordinatensystem meist als Längsachse definiert)

R_{x}={\begin{pmatrix}1&0&0&0\\0&\cos(\alpha )&\sin(\alpha )&0\\0&-\sin(\alpha )&\cos(\alpha )&0\\0&0&0&1\end{pmatrix}}

Um die Y-Achse (im Objektkoordinatensystem meist als Querachse definiert)

R_{y}={\begin{pmatrix}\cos(\alpha )&0&-\sin(\alpha )&0\\0&1&0&0\\\sin(\alpha )&0&\cos(\alpha )&0\\0&0&0&1\end{pmatrix}}

Um die Z-Achse (im Objektkoordinatensystem meist als Hochachse definiert)

R_{z}={\begin{pmatrix}\cos(\alpha )&\sin(\alpha )&0&0\\-\sin(\alpha )&\cos(\alpha )&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}

Zudem wenden wir eine Translationsmatrix an, die das Flugzeug an den gewünschten Punkt in unserer Welt verschiebt:

T_{x,y,z}={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\x&y&z&1\end{pmatrix}}

.

Anmerkung: Obige Matrizen sind gegenüber denjenigen im Artikel Drehmatrix transponiert. Die Erklärung dazu steht im folgenden Abschnitt.

Nun könnten wir die Position der Vertices des Flugzeugs in Weltkoordinaten berechnen, indem wir jeden Punkt nacheinander mit diesen vier Matrizen multiplizieren. Da die Multiplikation einer Matrix mit einem Vektor recht aufwendig ist, geht man meistens einen anderen Weg und multipliziert zunächst die vier Matrizen zusammen. Die Multiplikation zweier Matrizen ist zwar noch teurer, muss aber nur einmal für das ganze Objekt ausgeführt werden. Die Multiplikationen $((((v*R_{x})*R_{y})*R_{z})*T)$ und $(v*(((R_{x}*R_{y})*R_{z})*T))$ sind gleichwertig. Danach könnte die resultierende Matrix auf die Punkte angewendet werden. In der Praxis wird die Multiplikation mit den Punkten allerdings jetzt immer noch nicht angewendet, sondern zuerst die Kameramatrizen – siehe unten – bestimmt.

Für unser Beispiel von oben muss die Translation allerdings etwas anders bestimmt werden, da die Bedeutung von „Oben“ – außer am Nordpol – nicht mit der positiven Z-Achse übereinstimmt und daher das Modell auch noch um den Erdmittelpunkt gedreht werden muss.

T_{Kugel}=T_{x,y,z}(0,0,R+{hasl})*R_{y}(\Pi /2-{lat})*R_{z}({long})

Der erste Schritt schiebt den Ursprung des Modells in die richtige Höhe über der Erdoberfläche, danach wird um Länge und Breite rotiert.

Die Reihenfolge, in der die Matrizen angewendet werden, ist wichtig, denn die Matrizenmultiplikation ist nicht kommutativ. Das gilt auch für die drei Rotationen, wie man sich an einem Beispiel vor Augen führen kann: Der Punkt (1, 0, 0) liegt auf der X-Achse, wenn man den zunächst um jeweils 90° um die X- und dann um die Y-Achse rotiert, landet er auf der Z-Achse (die Rotation um die X-Achse hat keinen Effekt auf einen Punkt der auf der Achse liegt). Rotiert man hingegen zunächst um die Y- und dann um die X-Achse liegt der resultierende Punkt auf der Y-Achse. Die Reihenfolge an sich ist beliebig, solange man sie immer gleichmacht. Die Reihenfolge mit x, dann y, dann z (Roll, Pitch, Heading) ist häufig am intuitivsten, denn die Rotation bewirkt u. a., dass die Kompassrichtung mit der Richtung der „Nase“ übereinstimmt.

Es gibt außerdem zwei Konventionen, diese Matrizen zu definieren, und zwar abhängig davon, ob man mit Spaltenvektoren oder mit Zeilenvektoren arbeiten will. Verschiedene Grafikbibliotheken haben hier unterschiedliche Präferenzen. OpenGL beispielsweise bevorzugt Spaltenvektoren, DirectX Zeilenvektoren. Aus der Entscheidung folgt, von welcher Seite die Punktvektoren an die Transformationsmatrizen multipliziert werden. Für Spaltenvektoren erfolgt die Multiplikation von rechts, also $v_{out}=M*v_{in}$ , wobei v_out und v_in 4×1 Spaltenvektoren darstellen. Auch die Konkatenierung der Matrizen erfolgt von rechts nach links, also beispielsweise $M=T_{x}*R_{x}$ , wenn zuerst rotiert und dann verschoben werden soll. Bei Zeilenvektoren verhält es sich genau umgekehrt. Die Multiplikation erfolgt jetzt von links als $v_{out}=v_{in}*M$ mit 1×4-Vektoren und die Konkatenierung lautet $M=R_{x}*T_{x}$ wenn ebenfalls zunächst rotiert und dann verschoben wird. Die weiter oben dargestellten Matrizen gelten für den zweiten Fall, diejenigen für Spaltenvektoren ergeben sich als Transponierte davon. Es gilt die Regel $(v*M)^{T}=M^{T}*v^{T}$ ,[2] was für die Multiplikation mit Vektoren bedeutet, dass man durch die Transponierung die Multiplikationsreihenfolge vertauschen darf.

Das Interessante an dieser Matrixverkettung ist nun, dass durch jede solche Transformation ein neues Koordinatensystem definiert wird. Das lässt sich beliebig weiterziehen. So kann beispielsweise der Propeller des Flugzeuges als eigenes Modell vorliegen, das dann durch eine Translation an die Flugzeugnase platziert wird. Diese Translation muss nur noch die Verschiebung vom Modellkoordinatensystem ins Propellerkoordinatensystem beschreiben. Zum Zeichnen des gesamten Flugzeugs wird also zuerst die Transformationsmatrix für das Flugzeug bestimmt, die Punkte transformiert und dann anschließend die Translation zum Propellermodell auf die Matrix des Flugzeugs multipliziert und dann die Propellerpunkte transformiert.

Die auf diese Art berechnete Matrix nennt man auch die Welt-Matrix (englisch: World-Transformation). Sie muss für jedes Objekt der Welt vor der Darstellung bestimmt werden. Die Anwendung kann hier auf Veränderungen Einfluss nehmen, also beispielsweise die Position unseres Flugzeuges entsprechend der Geschwindigkeit ändern.

Kameratransformation

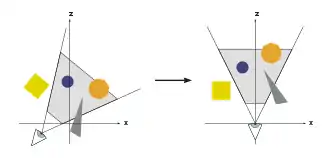
Links: Position und Richtung des virtuellen Betrachters, wie er vom Anwender definiert wurde, rechts: Platzierung der Objekte nach der Kameratransformation. Der hellgraue Bereich ist das Sichtvolumen.

Neben den Objekten definiert die Szene auch eine virtuelle Kamera oder einen Betrachter, der die Position und Blickrichtung angibt, aus der die Szene gerendert werden soll. Um die spätere Projektion und das Clipping zu vereinfachen, wird die Szene so transformiert, dass sich die Kamera am Ursprung befindet, mit Blickrichtung entlang der Z-Achse. Das resultierende Koordinatensystem wird Kamera-Koordinatensystem genannt und die Transformation Kameratransformation (englisch View-Transformation).

Die View-Matrix wird üblicherweise aus Kameraposition, Zielpunkt (wohin schaut die Kamera) und einem Up-Vektor („Oben“ aus Sicht des Betrachters) bestimmt. Zuerst werden drei Hilfsvektoren benötigt:

zaxis = normal(cameraPosition - cameraTarget)

xaxis = normal(cross(cameraUpVector, zaxis))

yaxis = cross(zaxis, xaxis)

Mit normal(v) = Normalisierung des Vektors v; cross(v1, v2) = Kreuzprodukt von v1 und v2.

Schließlich die Matrix:

{\begin{pmatrix}{xaxis}.x&{yaxis}.x&{zaxis}.x&0\\{xaxis}.y&{yaxis}.y&{zaxis}.y&0\\{xaxis}.z&{yaxis}.z&{zaxis}.z&0\\-{dot}({xaxis},{cameraPosition})&-{dot}({yaxis},{cameraPosition})&-{dot}({zaxis},{cameraPosition})&1\end{pmatrix}}

Mit dot(v1, v2) = Skalarprodukt von v1 und v2.

Projektion

Der Projektionsschritt transformiert das Sichtvolumen in einen Würfel mit den Eckpunktkoordinaten (−1, −1, −1) und (1, 1, 1); gelegentlich werden auch andere Zielvolumen verwendet. Dieser Schritt wird Projektion genannt, obwohl er ein Volumen in ein anderes Volumen transformiert, da die resultierenden Z-Koordinaten nicht im Bild gespeichert werden, sondern lediglich beim Z-Buffering im späteren Rasterungsschritt Anwendung finden. Bei einer perspektivischen Abbildung wird eine Zentralprojektion verwendet. Um die Anzahl der dargestellten Objekte zu begrenzen, werden zwei zusätzliche Clipping Planes verwendet; das Sichtvolumen ist hier also ein Pyramidenstumpf (Frustum). Die Parallel- oder Orthogonalprojektion wird beispielsweise für technische Darstellungen verwendet, denn sie hat den Vorteil, dass alle Parallelen im Objektraum auch im Bildraum parallel sind und Flächen und Volumina unabhängig von der Distanz zum Betrachter gleich groß sind. Landkarten verwenden beispielsweise auch eine Orthogonalprojektion (sogenanntes Orthofoto), Schrägbilder einer Landschaft sind so allerdings nicht zu gebrauchen denn – obwohl technisch natürlich darstellbar – erscheinen sie uns so verzerrt, dass wir damit nichts anfangen können.

Die Formel zur Berechnung einer perspektivischen Abbildungsmatrix ist:

{\begin{pmatrix}w&0&0&0\\0&h&0&0\\0&0&{far}/({near-far})&-1\\0&0&({near}*{far})/({near}-{far})&0\end{pmatrix}}

Mit h=cot(fieldOfView/2.0) (Öffnungswinkel der Kamera); w=h/aspectRatio (Seitenverhältnis des Zielbildes); near=Kleinste Distanz, die sichtbar sein soll; far=Weiteste Distanz, die sichtbar sein soll.

Die Gründe, weshalb die kleinste und die größte Distanz hier angegeben werden müssen, sind zum einen, dass durch diese Distanz dividiert wird, um die Größenskalierung zu erreichen (weiter entfernte Objekte werden in einer perspektivischen Abbildung kleiner als nahe Objekte) und zum anderen, dass damit die Z-Werte auf den Bereich 0..1 skaliert werden, womit dann der Z-Buffer gefüllt wird. Dieser hat oft nur eine Auflösung von 16 Bit, weshalb die Nah- und Fernwerte mit Bedacht gewählt werden sollten. Eine zu große Differenz zwischen dem nahen und dem fernen Wert führt wegen der geringen Auflösung des Z-Puffers zu sogenanntem Z-Fighting. Aus der Formel ist auch ersichtlich, dass der Nahwert nicht 0 sein kann, denn dieser Punkt ist der Fokuspunkt der Projektion. In diesem Punkt gibt es kein Bild.

Der Vollständigkeit halber noch die Formel für die Parallelprojektion (Orthogonale Projektion):

{\begin{pmatrix}2.0/w&0&0&0\\0&2.0/h&0&0\\0&0&1.0/({near-far})&-1\\0&0&{near}/({near}-{far})&0\end{pmatrix}}

Mit w=Breite des Zielwürfels (Dimension in Einheiten des Weltkoordinatensystems); h=w/aspectRatio (Seitenverhältnis des Zielbildes); near=Kleinste Distanz, die sichtbar sein soll; far=Weiteste Distanz, die sichtbar sein soll.

Aus Effizienzgründen werden die Kamera- und die Projektionsmatrix üblicherweise in eine Transformationsmatrix zusammengefasst, sodass das Kamerakoordinatensystem übergangen wird. Die resultierende Matrix ist üblicherweise für ein einzelnes Bild gleichbleibend, während die Weltmatrix für jedes Objekt anders aussieht. In der Praxis werden daher View- und Projection vorberechnet, so dass während der Darstellung nur noch die World-Matrix angepasst werden muss. Es sind jedoch weitere, aufwändigere Transformationen wie Vertex Blending möglich. Frei programmierbare Geometrie-Shader, die die Geometrie verändern, können ebenfalls ausgeführt werden. Im eigentlichen Renderschritt wird dann Weltmatrix*Kameramatrix*Projektionsmatrix gerechnet und diese dann endlich auf jeden einzelnen Punkt angewendet. Damit werden die Punkte aller Objekte direkt ins Bildschirmkoordinatensystem überführt (zumindest fast, die Wertebereiche der Achsen sind für den sichtbaren Bereich noch −1..1, siehe Abschnitt „Window-Viewport-Transformation“).

Beleuchtung

Oft enthält eine Szene an verschiedenen Positionen platzierte Lichtquellen, um die Beleuchtung der Objekte realistischer erscheinen zu lassen. In diesem Fall wird für jeden Vertex anhand der Lichtquellen und den zum entsprechenden Dreieck gehörenden Materialeigenschaften ein Verstärkungsfaktor für die Textur berechnet. Im späteren Rasterungsschritt werden die Eckpunktwerte eines Dreiecks über dessen Fläche interpoliert. Eine allgemeine Beleuchtung (ambient light) wird auf alle Flächen angewendet. Es ist die diffuse und damit richtungsunabhängige Helligkeit der Szene. Die Sonne ist eine gerichtete Lichtquelle, die als unendlich weit entfernt angenommen werden kann. Die Beleuchtung, die die Sonne auf einer Fläche bewirkt, wird durch Bilden des Skalarproduktes des Richtungsvektors von der Sonne und des Normalvektors der Fläche bestimmt. Ist der Wert negativ, ist die Fläche der Sonne zugewandt.

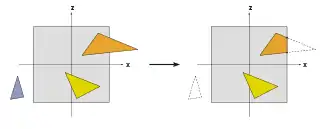
Clipping von Primitiven gegen den Würfel. Das blaue Dreieck wird verworfen, während das orange Dreieck geclippt wird, wobei zwei neue Vertices erzeugt werden.

Clipping

Nur die Primitive, die sich innerhalb des Sichtvolumens befinden, müssen auch tatsächlich gerastert werden. Primitiven, die sich vollständig außerhalb des Sichtvolumens befinden, werden verworfen; dies wird Frustum Culling genannt. Weitere Culling-Verfahren wie Backface Culling, die die Zahl der zu berücksichtigenden Primitiven reduzieren, können theoretisch in einem beliebigen Schritt der Grafikpipeline ausgeführt werden. Primitiven, die sich nur teilweise im Innern des Würfels befinden, müssen gegen den Würfel geclippt werden. Der Vorteil des vorherigen Projektionsschrittes liegt darin, dass das Clipping stets gegen den gleichen Würfel stattfindet. Nur die – eventuell geclippten – Primitiven, die sich innerhalb des Sichtvolumens befinden, werden an den nächsten Schritt weitergeleitet.

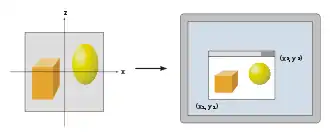
Window-Viewport-Transformation

Um das Bild an einem beliebigen Zielbereich (Viewport) des Bildschirms auszugeben, muss eine weitere Transformation, die Window-Viewport-Transformation, angewandt werden. Dabei handelt es sich um eine Verschiebung, gefolgt von einer Skalierung. Die resultierenden Koordinaten sind die Gerätekoordinaten des Ausgabegeräts. Der Viewport enthält 6 Werte: Höhe und Breite des Fensters in Pixeln, die linke, obere Ecke des Fensters in Fensterkoordinaten (meist 0, 0) und die Minimum- und Maximumwerte für Z (meist 0 und 1).

Damit ist

{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}{vp}.X+(1.0+v.X)*{vp}.{width}/2.0\\{vp}.Y+(1.0-v.Y)*{vp}.{height}/2.0\\{vp}.{minz}+v.Z*({vp}.{maxz}-{vp}.{minz})\end{pmatrix}}

Mit vp=Viewport; v=Punkt nach Projektion

Auf moderner Hardware werden die meisten Schritte der Geometrie-Berechnung im Vertex-Shader durchgeführt. Dieser ist im Prinzip frei programmierbar, übernimmt aber in der Regel mindestens die Transformation der Punkte und die Beleuchtungsberechnung. Für die Programmierschnittstelle DirectX ist ab Version 10 der Einsatz eines benutzerdefinierten Vertex-Shaders unumgänglich, während ältere Versionen noch einen Standard-Shader zur Verfügung gestellt haben.

Rasterung

Im Rasterungsschritt werden alle Primitiven gerastert, es werden also aus kontinuierlichen Flächen diskrete Fragmente erstellt.

In dieser Stufe der Grafikpipeline werden zur besseren Unterscheidbarkeit die Rasterpunkte auch Fragmente genannt, d. h. jedes Fragment entspricht einem Pixel im Framebuffer und dieses entspricht einem Pixel des Bildschirms.

Diese können dann eingefärbt (ggf. beleuchtet) werden. Des Weiteren ist es nötig, bei überlappenden Polygonen das jeweils sichtbare, also näher am Betrachter liegende, zu ermitteln. Für diese sogenannte Verdeckungsberechnung wird üblicherweise ein Z-Buffer verwendet. Die Farbe eines Fragments hängt von der Beleuchtung, Textur und anderen Materialeigenschaften des sichtbaren Primitivs ab und wird oft anhand der Dreieckseckpunkte interpoliert. Wo vorhanden, wird ein Fragment-Shader im Rasterungsschritt für jedes Fragment des Objektes durchlaufen. Sollte ein Fragment sichtbar sein, kann es nun mit bereits vorhandenen Farbwerten im Bild gemischt werden, falls Transparenzen simuliert werden oder Multi-Sampling verwendet wird. In diesem Schritt wird aus einem oder mehreren Fragmenten ein Pixel.

Damit der Anwender nicht die allmähliche Rasterung der Primitiven sieht, findet Doppelpufferung statt. Die Rasterung erfolgt dabei in einem besonderen Speicherbereich. Sobald das Bild komplett gerastert wurde, wird es auf einmal in den sichtbaren Bereich des Bildspeichers kopiert.

Inverse

Alle verwendeten Matrizen sind regulär und damit invertierbar. Da durch die Multiplikation zweier regulärer Matrizen wieder eine reguläre Matrix entsteht, ist auch die gesamte Transformationsmatrix invertierbar. Die Inverse wird benötigt, um aus Bildschirmkoordinaten wieder Weltkoordinaten zu berechnen – beispielsweise um aus der Mauszeigerposition auf das geklickte Objekt zu schließen. Da aber der Bildschirm und die Maus nur zwei Dimensionen haben, ist die dritte unbekannt. Es wird daher ein Strahl an der Cursorposition in die Welt projiziert und dann der Schnittpunkt dieses Strahles mit den Polygonen in der Welt bestimmt.

Shader

Klassische Grafikkarten orientierten sich im internen Aufbau noch relativ eng an der Grafik-Pipeline. Mit steigenden Anforderungen an die GPU wurden Einschränkungen schrittweise aufgehoben, um mehr Flexibilität zu schaffen. Moderne Grafikkarten nutzen eine frei programmierbare shadergesteuerte Pipeline, die es erlaubt, direkt in einzelne Bearbeitungsschritte einzugreifen. Um den Hauptprozessor zu entlasten, wurden zusätzliche Bearbeitungsschritte innerhalb der Pipeline eingeführt, die bislang nur auf der CPU liefen.

Die wichtigsten Shadereinheiten sind Pixel-Shader, Vertex-Shader und Geometrie-Shader. Um alle Einheiten optimal auszunutzen, wurde der Unified-Shader eingeführt. Dadurch gibt es nur noch einen einheitlichen großen Pool von Shader-Einheiten. Je nach Bedarf wird der Pool in unterschiedlichen Gruppen von Shadern aufgeteilt. Eine strikte Trennung zwischen den Shader-Typen ist daher nicht mehr sinnvoll. Inzwischen ist es auch möglich, über einen sogenannten Compute-Shader beliebige Berechnungen abseits der Darstellung von einer Grafik auf der GPU ausführen zu lassen. Der Vorteil liegt darin, dass diese stark parallelisiert laufen, es gibt dabei jedoch Einschränkungen. Diese universellen Berechnungen werden auch GPGPU genannt.

Literatur

Tomas Akenine-Möller, Eric Haines: Real-Time Rendering. AK Peters, Natick MA 2002, ISBN 1-56881-182-9.
Michael Bender, Manfred Brill: Computergrafik: ein anwendungsorientiertes Lehrbuch. Hanser, München 2006, ISBN 3-446-40434-1.
Martin Fischer: Pixel-Fabrik. Wie Grafikchips Spielewelten auf den Schirm zaubern. In: c’t Magazin für Computer Technik. Heise Zeitschriften Verlag, 4. Juli 2011, S. 180.

Einzelnachweise

Tomas Akenine-Möller, Eric Haines: Real-Time Rendering. S. 11.
K. Nipp, D. Stoffer; Lineare Algebra; v/d/f Hochschulverlag der ETH Zürich; Zürich 1998, ISBN 3-7281-2649-7.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Tomas Akenine-Möller, Eric Haines: Real-Time Rendering. S. 11.

[2] K. Nipp, D. Stoffer; Lineare Algebra; v/d/f Hochschulverlag der ETH Zürich; Zürich 1998, ISBN 3-7281-2649-7.