Antialiasing (Computergrafik)
Antialiasing (AA, auch Anti-Aliasing oder Kantenglättung) ist die Verminderung von unerwünschten Effekten, die durch das begrenzte Pixelraster (siehe Bildauflösung und Alias-Effekt) oder durch den Treppeneffekt bei der Erzeugung einer Computergrafik (computergenerierte 2D- oder 3D-Grafiken) entstehen können.

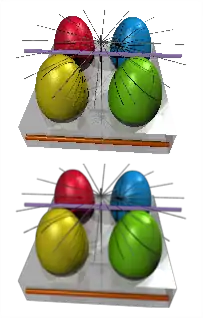
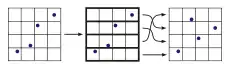
Beim Antialiasing werden die Bildinhalte üblicherweise nicht nur am Pixel, sondern auch an anderen Positionen ausgewertet (abgetastet) und in die Berechnung der Pixelfarbe mit einbezogen. Daneben verringern einige für das Echtzeitrendern entwickelte Techniken den Treppeneffekt durch nachträgliche Filterung oder Nachzeichnung des Bildes.
Antialiasing-Methoden unterscheiden sich durch das zur Verteilung der Abtastpunkte verwendete Schema sowie durch die Wahl des Rekonstruktionsfilters, der bestimmt, wie die an den Abtastpunkten ermittelten Farbwerte gewichtet werden.
Hintergrund
Abtastung und Prealiasing
Die Erzeugung einer Rastergrafik aus einer Bildbeschreibung per Rasterung oder Bildsynthese besteht letzten Endes darin, jedem diskreten Pixel eine Farbe zuzuweisen. Dieser Vorgang kann im Rahmen der Theorie der Signalverarbeitung als Abtastung eines Signals interpretiert werden. Die Computergrafik ist insofern einzigartig, als hier viele Signale als abstrakte Bildbeschreibungen vorliegen, die nur an einzelnen Punkten algorithmisch ausgewertet werden können. Ein Beispiel sind Bilder, die mittels Raytracing berechnet werden. Derartige Signale können auch als prozedurale Signale bezeichnet werden.[1]
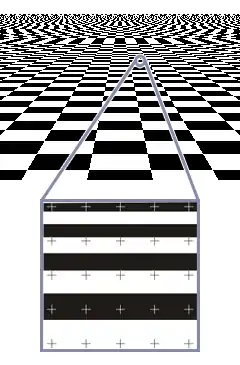
Beim Rastern ohne Antialiasing wird die Bildbeschreibung ausschließlich an den Pixeln ausgewertet; andere Punkte des Bildes fließen nicht in die Farbe der Pixel mit ein. Ein Problem mit dieser Methode ist, dass kleine Figuren nicht vom Pixelraster erfasst werden und somit im gerasterten Bild nicht auftauchen. Wenn kleine Bilddetails regelmäßig angeordnet sind, interferieren sie mit dem Pixelraster, was zu Alias-Effekten führt. Dies wird durch nebenstehendes computergeneriertes Bild eines unendlich großen Schachbretts illustriert.
Die Periodenlänge des Signals ist hier gleich der Größe zweier projizierter Schachbrettfelder. Sobald die Periodenlänge zwei Pixelabstände unterschreitet, also die Nyquist-Frequenz überschritten wird, wird das Signal unterabgetastet. Bestimmte Schachbrettfelder werden jetzt vom Pixelraster nicht mehr erfasst; das Schachbrettmuster wird zerstört. Gemäß dem Nyquist-Shannon-Abtasttheorem treten Alias-Effekte auf, bei denen sich eine hohe Originalfrequenz in der Abtastung als irreführende niedrige Frequenz äußert: Nahe dem Horizont entsteht der falsche Eindruck, das Originalsignal würde merkwürdig große Felder enthalten. Der im Deutschen gelegentlich verwendete illustrierende Begriff „Lattenzauneffekt“ macht dies deutlich: Man betrachtet das Ortsfrequenzspektrum des Originalbildes durch eine vom Wiedergabegerät, z. B. dem Bildschirm, fest vorgegebene Frequenzauflösung – den Lattenzaun.[2] Diese Art von Alias-Effekten, die ein Resultat der Abtastmethode sind, wird Prealiasing genannt.[1]
Auch wenn das Bild mit höheren Bildauflösungen und damit höheren Abtastraten berechnet würde, würden störende Aliasing-Effekte nahe dem Horizont auftauchen, allerdings erst ab einer höheren Frequenz. Das liegt daran, dass in der Schachbrettszene die Felder zum Horizont hin immer kleiner werden und somit die Ortsfrequenz unbegrenzt ist.
Rekonstruktion und Postaliasing
In der Signalverarbeitung bezeichnet Rekonstruktion die Umwandlung eines diskreten in ein kontinuierliches Signal, indem zwischen den einzelnen Abtastwerten mittels eines Rekonstruktionsfilters interpoliert wird. In der Computergrafik wird der Begriff etwas anders interpretiert, da hier gar kein kontinuierliches Signal erzeugt wird. Vielmehr bedeutet Rekonstruktion in diesem Zusammenhang, die Farbe eines Pixels aus den Farbwerten in der Nähe des Pixels zu berechnen, zum Beispiel um eine Rastergrafik zu skalieren.[3] Beim dabei verwendeten Rekonstruktionsfilter handelt es sich um eine zweidimensionale Funktion, die über dem zu berechnenden Pixel zentriert ist und angibt, wie Abtastwerte gewichtet werden. So wird bei einem kegelförmigen Filter ein direkt am Pixel ermittelter Farbwert am höchsten gewichtet, während weiter entfernte Werte weniger Einfluss haben. Außerhalb des Trägers des Rekonstruktionsfilters liegende Farbwerte werden ignoriert. Der Farbwert des Pixels ist die Summe der gewichteten Farbwerte. Diese Operation entspricht einer Faltung mit einem Tiefpassfilter von einer Ordnung der gewählten Antialiasing-Stufe.
Das Antialiasing mittels Box-Filter, das den Mittelwert aller Farbwerte innerhalb eines um das Pixel gelegten Quadrates berechnet, wird auch als „ungewichtete Flächenabtastung“ (Unweighted Area Sampling) bezeichnet. In anderen Fällen spricht man von „gewichteter Flächenabtastung“ (Weighted Area Sampling).[4] Beispiele für Rekonstruktionsfilter bei gewichteter Flächenabtastung sind die Mitchell-Netravali-Filter (bikubische Filter), das Lanczos-Filter oder das Gauß-Filter.
- Antialiasing mit verschiedenen Rekonstruktionsfiltern
 Box-Filter (ungewichtete Flächenabtastung)
Box-Filter (ungewichtete Flächenabtastung) Mitchell-Netravali-Filter mit Parameterwahl B=C=⅓
Mitchell-Netravali-Filter mit Parameterwahl B=C=⅓ Lanczos-Filter mit Radius 2
Lanczos-Filter mit Radius 2
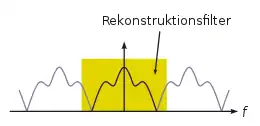
Ein abgetastetes, diskretes Signal ist im Frequenzbereich eine Reihe von frequenzversetzten Kopien des Nutzsignals. Die Rekonstruktion kann als Isolation des originalen Nutzsignals unter Ausschluss der Kopien interpretiert werden. Wenn der Rekonstruktionsfilter nicht nur das Nutzsignal isoliert, sondern auch Teile von dessen Kopien mit einbezieht (siehe Schema rechts), kommt es zu Postaliasing.[1] Postaliasing entsteht also durch die Wahl eines ungeeigneten Rekonstruktionsfilters und kann selbst dann auftreten, wenn das Originalsignal mit einer ausreichenden Abtastrate und ohne Prealiasing abgetastet wurde.

Treppeneffekt

Der Begriff Treppeneffekt bezeichnet das kantige, „treppenartige“ Erscheinungsbild gerasterter Figuren. In der Fachliteratur wurde oft behauptet, dass der Treppeneffekt eine Folge des Alias-Effekts sei. Dies ist jedoch falsch, wie sich anhand eines Vergleichs der Fourier-Transformationen des idealen und des gerasterten Bildes zeigen lässt.[5] Der Treppeneffekt äußert sich nicht, indem eine hohe Frequenz als störende niedrige Frequenz erscheint, sondern ist eine direkte Konsequenz der begrenzten Auflösung des Ausgabegerätes. Besonders bei Animationen ist der Treppeneffekt auffallend, da sich hier Figuren scheinbar ruckartig bewegen und sehr dünne oder kleine Objekte bei der Bewegung zu flimmern scheinen.
Verfahren
Ohne Anwendung von Antialiasing wird für jedes Pixel nur einmalig an einer relativ zum Pixel gleichbleibenden Position abgetastet. Beim Antialiasing wird die Bildbeschreibung an mehreren und/oder relativ zum Pixel unterschiedlichen Positionen ausgewertet. Aus den so ermittelten Werten wird die Farbe des Pixels gemäß einem Rekonstruktionsfilter berechnet. Durch die Wahl eines geeigneten Abtastverfahrens lässt sich Prealiasing, durch die Wahl geeigneter Rekonstruktionsfilter Postaliasing vermindern oder vermeiden. Die Bezeichnung „Antialiasing“ ist insofern irreführend, als Antialiasing nicht nur gegen Alias-Effekte, sondern auch gegen den Treppeneffekt und andere unerwünschte Effekte, etwa durch das Pixelraster fallende kleine Figuren, angewandt wird. Franklin Crow lieferte 1977 die erste Beschreibung des Alias-Effekts als Ursache von Bildartefakten in Computergrafiken.[6]
Die traditionellen Antialiasing-Techniken der Signalverarbeitung sind nicht ohne Weiteres auf die Computergrafik übertragbar. Dies liegt daran, dass vom Standpunkt der Signalverarbeitung betrachtet Computergrafiken im Gegensatz beispielsweise zu Audiosignalen folgende Besonderheiten aufweisen:
- Die in der Computergrafik vorkommenden Signale sind künstliche, abstrakte Bildbeschreibungen, die oft nicht in ihrer Gesamtheit erfasst, sondern nur an einzelnen Punkten ausgewertet werden können.
- Computergrafiken enthalten üblicherweise harte Objektkanten, was stellenweise unendlichen Ortsfrequenzen entspricht. Daher ist eine perfekte Rekonstruktion des Ausgangssignals mittels idealem Tiefpass (Sinc-Filter) nicht möglich.
- Bildbeschreibungen werden häufig nicht regelmäßig, sondern an unregelmäßig verteilten Positionen abgetastet.
- Die menschliche visuelle Wahrnehmung reagiert besonders empfindlich auf die durch weniger gute Antialiasing-Methoden verursachten Artefakte.
Praktische Gesichtspunkte
Damit Antialiasing die beste Wirkung erzielt, ist es unerlässlich, Gammakorrektur anzuwenden. Linien und Polygonkanten, die mit Antialiasing, aber ohne Gammakorrektur gerastert wurden, tendieren zu einem „seilartigen“ Aussehen.[7] Antialiasing lässt sich auch mit Subpixel-Rendering kombinieren, um von der horizontalen Unterteilung eines Bildschirmpixels in nebeneinander liegende Grundfarben zu profitieren. Im Bereich der Pixel-Art geschieht Kantenglättung nicht automatisch, sondern wird vom Grafiker direkt durch das Setzen einzelner Pixel erreicht.
Antialiasing nimmt zusätzliche Rechenleistung in Anspruch, die besonders beim Echtzeitrendern nicht vernachlässigbar ist. Ein weiterer Nachteil ist, dass ein mit Antialiasing erzeugtes Bild als unscharf empfunden werden kann; die Unschärfe hängt ebenso wie andere Mängel vom verwendeten Rekonstruktionsfilter ab. Umgekehrt stellt die bloße nachträgliche Weichzeichnung eines gerasterten Bildes kein konventionelles Antialiasing dar, da hierbei die ursprüngliche Bildbeschreibung nicht ausgewertet wird; dennoch basieren einige Techniken aus dem Echtzeitbereich auf einer solchen Verfahrensweise (siehe Abschnitt Hardware-Implementierung). Bilder, die bereits Prealiasing-Effekte aufweisen, etwa mit niedriger Auflösung gescannte Druckraster, lassen sich zum Teil nachträglich im Frequenzbereich durch Beseitigung der störenden Fourierkomponenten korrigieren. Es existieren außerdem Techniken, um Treppeneffekte bei Bildern, die ohne Antialiasing erzeugt wurden, zu entfernen.[8]
Prefiltering und Flächenabtastung
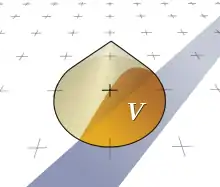
In der Computergrafik bezeichnet Prefiltering die Ermittlung der Farbe eines Pixels, ohne dass einzelne Abtastungen vorgenommen werden. Vielmehr wird die Farbe direkt anhand der Bildbeschreibung berechnet. Wie oben beschrieben, entspricht der Farbwert eines Pixels der vom Rekonstruktionsfilter gewichteten Summe aller Farbwerte der Objekte, die vom Träger des Filters überlappt werden. Prefiltering ist nur bei Bildbeschreibungen möglich, deren Faltung mit dem Rekonstruktionsfilter analytisch berechenbar ist, also in Form bekannter Funktionen ausgedrückt werden kann. Hierzu zählen einfache geometrische Objekte wie Linien. Auf prozedurale Signale kann Prefiltering hingegen nicht angewandt werden, da diese nur an individuellen Punkten abgetastet werden können.
Eines der ersten Prefiltering-Verfahren für Computergrafiken wurde 1978 von Edwin Catmull beschrieben.[9] Sein Algorithmus verwendet Unweighted Area Sampling. Die Farbe eines Pixels wird berechnet, indem die Polygone, aus denen sich das Bild zusammensetzt, gegen das Pixel geclippt werden und so deren Flächenanteil ermittelt werden kann. Dieses Verfahren war so langsam, dass es nur bei zweidimensionalen Computeranimationen mit einigen großen Polygonen eingesetzt werden konnte.[10] Spätere Methoden versuchten, die Flächenanteile der Objektfragmente mittels Bitmasken zu approximieren[11][12] – darunter Carpenters A-Buffer, manchmal auch Multisampling genannt[13] – oder Lookup-Tabellen zu verwenden.[14] Daneben wurden auf die Rasterung von Grundformen wie Linien und Kreisen zugeschnittene Antialiasing-Verfahren entwickelt, siehe Rasterung von Linien und Rasterung von Kreisen. Auch hochwertiges Prefiltering-Antialiasing beliebiger Kurven mit verschiedenen Rekonstruktionsfiltern ist möglich.[15]
Postfiltering und Punktabtastung
Postfiltering oder Supersampling wird vornehmlich angewandt, wenn die Bildbeschreibung nur an einzelnen Punkten ausgewertet werden kann. Dazu werden zur Berechnung der Farbe eines jeden Pixels mehrere Abtastwerte herangezogen, die mittels eines Rekonstruktionsfilters gewichtet werden. Mathematisch betrachtet ist Postfiltering eine Methode zur numerischen Annäherung des Faltungsintegrals.
Multisampling-Methoden unterscheiden sich in der Anzahl und Verteilung der Abtastpositionen pro Pixel. Beim Echtzeitrendern wird meist für alle Pixel das gleiche Muster verwendet. Einige Muster legen für die Abtastwerte unterschiedliche Wichtungen fest, weshalb sie auch als lineare Rekonstruktionsfilter betrachtet werden können. Wenn der Träger eines Rekonstruktionfilters über mehrere Pixel reicht und sich mehrere Pixel einige Abtastwerte teilen, spricht man von Sample Sharing.[16]
Folgende geordnete Muster sind gebräuchlich:

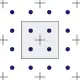 |
Geordnet. Die Abtastpositionen sind kachelförmig entlang den Achsen verteilt. |
 |
Schachbrett. Die Abtastpositionen sind wie ein Schachbrettmuster verteilt. |
 |
RGSS. Dieses Muster, genannt Rotated Grid SuperSampling, ergibt für nahezu horizontale oder vertikale Kanten, bei denen Antialiasing am nötigsten ist, bessere Ergebnisse als das geordnete Muster. |
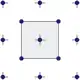 |
Quincunx. Bei diesem von Nvidia entwickelten Muster, auch High Resolution Antialiasing (HRAA) genannt, teilen sich jeweils vier Pixel die Abtastwerte in den Ecken, die jeweils nur zu einem Viertel des Abtastwerts in der Mitte gewichtet werden.[17] Zusammen mit der Position in der Mitte sind im Mittel nur zwei Abtastungen pro Pixel nötig. |
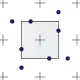 |
Flipquad. Vier Abtastwerte werden von je zwei Pixeln geteilt; für benachbarte Pixel ist das Muster spiegelverkehrt.[18] Damit ergibt sich ein Durchschnitt von zwei Abtastungen pro Pixel. |
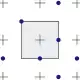 |
Fliptri. Es werden drei Abtastwerte für jedes Pixel herangezogen. Einer der Werte wird von vier Pixeln geteilt, die beiden anderen von zwei Pixeln. Im Mittel sind damit nur 1,25 Abtastungen pro Pixel nötig. Für dieses Muster können unterschiedliche Wichtungen verwendet werden.[19] Kombinationen des Flipquad- und Fliptri-Musters sind ebenfalls möglich.[20] |
Im Gegensatz zu den geordneten Mustern variiert bei der stochastischen Abtastung das Abtastmuster relativ zum Pixel. Dadurch werden Alias-Effekte durch Rauschen ersetzt, das als weniger irritierend wahrgenommen wird. Gleichzeitig ist es jedoch wünschenswert, die Abtastpunkte weit entfernt voneinander zu halten, um eine möglichst repräsentative Abtastung zu gewährleisten. Stochastische Abtastmuster werden vor allem in der realistischen Bildsynthese verwendet.

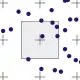 |
Zufällige Verteilung. Die Abtastpositionen werden von einem Pseudozufallszahlengenerator bestimmt. Dabei kommt es zu einer unerwünschten örtlichen Anhäufung von Positionen. |
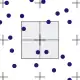 |
Jittering. Der Bereich um ein Pixel wird regelmäßig in Quadrate aufgeteilt, in denen jeweils eine Abtastposition zufällig verteilt wird. Die Anhäufung von Abtastpositionen wird dadurch verringert; es können jedoch nur genau Abtastpunkte pro Pixel verwendet werden. |
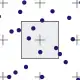 |
N-Rooks. Bei diesem Schema, auch Latin Hypercube Sampling genannt, befindet sich in jeder Spalte und Zeile eines Gitters nur ein Abtastpunkt. Dazu wird zunächst in jeder Zelle entlang der Gitterdiagonale eine Abtastposition zufällig platziert, anschließend werden die Zeilen des Gitters zufällig vertauscht:
|
 |
Niedrigdiskrepante Verteilung. Zur Erzeugung der Abtastpositionen werden niedrigdiskrepante Folgen wie etwa die Halton-Folge verwendet, die weit voneinander entfernte Elemente erzeugen. |
 |
Poisson Disk. Bei der Poisson-Disk-Abtastung sind die Abtastpositionen zufällig verteilt, wobei sichergestellt wird, dass sie einen Mindestabstand zueinander haben. Zur Erzeugung von Poisson-Disk-Verteilungen wurden zahlreiche Methoden mit unterschiedlicher Qualität und Effizienz entwickelt.[21] |
Eine weitere Methode ist Adaptive Supersampling. Dabei wird die Anzahl der Abtastpunkte über das Bild variiert. Die Entscheidung, ob weitere Abtastungen vorgenommen werden sollen, wird anhand von lokalen Kriterien wie Kontrast gefällt.[22] Derartige Techniken sind allerdings in der Regel nicht erwartungstreu und können zu Artefakten führen.[23]
Anstatt die Abtastpunkte mehr oder weniger gleichmäßig zu verteilen und die dort ermittelten Werte durch einen Rekonstruktionsfilter zu gewichten, kann zur Berechnung der Pixelfarbe Importance Sampling angewandt werden. Hierbei werden die Abtastwerte entsprechend der Form des Rekonstruktionsfilters verteilt (mehr Abtastpunkte nahe beim Pixel) und gleich gewichtet. Diese Methode führt zu einem weniger verrauschten Ergebnis.[24]
Hardware-Implementierung
Zum Echtzeitrendern mittels Grafikkarten kann Antialiasing direkt in Hardware implementiert werden. Zunächst unterstützten nur sehr hochwertige und teure Grafikkarten diese Technik in Grafikschnittstellen wie OpenGL. Mit dem Aufkommen erschwinglicher Desktop-Grafikchips mit hoher Performance wie dem 3dfx VSA-100 oder dem NV10 von Nvidia wurde Echtzeit-Antialiasing auch für den normalen Anwender verfügbar.
Die konzeptuell einfachste Methode ist Full-Scene Antialiasing (FSAA). Dabei werden die Bilder mit höherer Auflösung gerendert und anschließend heruntergerechnet. Eine andere Methode verwendet den Akkumulationspuffer. Um ein Bild mit vier Abtastpunkten pro Pixel zu rendern, werden nacheinander vier Bilder in den Puffer geschrieben, die jeweils um den Bruchteil eines Pixelabstands in alle Richtungen versetzt sind. Eine Variante des Akkumulationspuffers ist der T-Buffer. Er besteht aus zwei, vier oder mehr Bild- und Z-Buffern, von denen jeder zum Rendern verwendet werden kann. Eine Maske bestimmt, wohin ein Dreieck gesendet wird; am Ende werden alle Puffer kombiniert. Wenn für jeden Puffer individuell ein Bildschirmoffset gesetzt wird, lässt sich Antialiasing erzielen, indem jedes Dreieck parallel an alle Puffer gesendet wird. Der Vorteil des Akkumulationspuffers und des T-Buffers ist, dass nicht nur geordnete Abtastpositionen möglich sind. Häufig wird auch sogenanntes Multisampling verwendet, das sich insofern von Supersampling unterscheidet, als nicht für jede Abtastposition Shader-Berechnungen durchgeführt werden.[16]
Als Prefiltering-Algorithmus kann auch der A-Buffer in Hardware implementiert werden.[25] Es wurden weitere hardwarebasierte Prefiltering-Algorithmen veröffentlicht, darunter das Z³-Verfahren,[26] das in ähnlicher Form von Matrox unter dem Namen Fragment Antialiasing (FAA) eingeführt wurde. Der Vorteil von Prefiltering ist, dass nur auf die Bereiche mit Polygonkanten tatsächlich Antialiasing angewendet wird.
In der Praxis werden beim Echtzeit-Antialiasing oft nur wenige Abtastwerte pro Pixel und das Box-Filter oder einfache lineare Rekonstruktionsfilter verwendet. Mindestens eine Grafikkarte, die Wildcat von 3DLabs, verwendet mit Jittering eine stochastische Abtastmethode. Das professionelle SAGE-Grafiksystem von Sun Microsystems erlaubt ein über 128 × 128 Pixel reichendes, programmierbares Abtastmuster mit gewichtetem Rekonstruktionsfilter.[27]
Eine weitere, von DirectX unterstützte Methode ist Edge Antialiasing.[28] Dabei werden nach dem Rendern der Szene die Objektkanten in einem zweiten Durchgang mit geglätteten Linien nachgezeichnet. Beim Deferred Shading, eine in einigen neueren Computerspielen angewandte Technik, wird die Geometrie der Objekte unabhängig von ihrer Beleuchtung berechnet. Da hierbei kein herkömmliches Hardware-Antialiasing anwendbar ist, kann der Treppeneffekt durch Kantendetektion und Weichzeichnung der Objektkanten kaschiert werden.[29] Eine ähnliche Methode ist Morphological Antialiasing (MLAA). Hierbei bestimmt das Pixelmuster an den Kanten die Art der Weichzeichnung.[30]
Die perspektivische Darstellung von Texturen beim Echtzeitrendern wird gelegentlich als „Textur-Antialiasing“ bezeichnet. Die dabei verwendeten Techniken wie Mip Mapping und anisotropes Filtern führen jedoch kein Antialiasing im üblichen Sinn durch, da keine neuen Bilder aus einer mathematischen Bildbeschreibung generiert werden. Vielmehr werden beim Texture Mapping existierende Rastergrafiken perspektivisch skaliert, außer bei prozeduralen Texturen, die während des Rendervorgangs berechnet werden.
Literatur
- Tomas Akenine-Möller, Eric Haines: Real-Time Rendering. AK Peters, Natick Mass 2002, ISBN 1-56881-182-9, S. 84–101.
- James Foley u. a.: Computer Graphics: Principles and Practice. Addison-Wesley, Reading 1995, ISBN 0-201-84840-6, besonders S. 617–647.
- Matt Pharr, Greg Humphreys: Physically Based Rendering. From Theory to Implementation. Morgan Kaufmann, London 2004, ISBN 0-12-553180-X, S. 279–367 (PDF; 7 MB).
- Alan Watt: 3D Computer Graphics. Addison-Wesley, Harlow 2000, ISBN 0-201-39855-9, S. 392–417.
Weblinks
Einzelnachweise
- Don Mitchell, Arun Netravali: Reconstruction Filters in Computer Graphics. ACM SIGGRAPH Computer Graphics 22, 4 (Aug. 1988): 221–228, ISSN 0097-8930
- Beate Meffert, Olaf Hochmuth: Werkzeuge der Signalverarbeitung: Grundlagen, Anwendungsbeispiele, Übungsaufgaben. Pearson Studium, München 2004, ISBN 3-8273-7065-5, S. 180 ff.
- Alan Watt: 3D Computer Graphics. S. 399.
- James Foley u. a.: Computer Graphics: Principles and Practice. S. 132–137.
- Alan Watt: 3D Computer Graphics. S. 397.
- Franklin Crow: The Aliasing Problem in Computer-Generated Shaded Images. Communications of the ACM 20, 11 (November 1977): 799–805, ISSN 0001-0782
- A. R. Forrest: Antialiasing In Practice. In: R. A. Earnshaw (Hrsg.): Fundamental Algorithms for Computer Graphics (= NATO ASI Series F.17). Springer, Berlin 1985, ISBN 3-540-13920-6, S. 113–134.
- Lei Yang u. a.: Antialiasing recovery. ACM Transactions on Graphics 30, 3 (Mai 2011): 22:1–22:9, ISSN 0730-0301 (Online)
- Edwin Catmull: A Hidden-Surface Algorithm with Anti-Aliasing. ACM SIGGRAPH Computer Graphics 12, 3 (Aug. 1978): 6–11
- Alan Watt: 3D Computer Graphics. S. 403.
- Loren Carpenter: The A-Buffer, an Antialiased Hidden Surface Method. In: SIGGRAPH ’84 Proceedings. ACM, New York 1984, ISBN 0-89791-138-5, S. 103–108.
- Eugene Fiume u. a.: A Parallel Scan Conversion Algorithm with Anti-Aliasing for a General-Purpose Ultracomputer. In: SIGGRAPH ’83 Proceedings. ACM, New York 1983, ISBN 0-89791-109-1, S. 141–150.
- Tomas Akenine-Möller, Eric Haines: Real-Time Rendering. S. 94.
- Greg Abram, Lee Westover: Efficient Alias-Free Rendering Using Bit-Masks and Look-Up Tables. ACM SIGGRAPH Computer Graphics 19, 3 (July 1985): 53–59
- A. E. Fabris, A. R. Forrest: Antialiasing of Curves by Discrete Pre-filtering. In: SIGGRAPH ’97 Proceedings. ACM Press, New York 1997, ISBN 0-89791-896-7, S. 317–326 (Online).
- Samuli Laine, Timo Aila: A Weighted Error Metric and Optimization Method for Antialiasing Patterns. Computer Graphics Forum 25, 1 (Mar. 2006): 83–94, ISSN 1467-8659 (PDF; 420 kB (Memento vom 8. Mai 2006 im Internet Archive))
- NVIDIA Corporation: HRAA: High-resolution Antialiasing through Multisampling. Technical Brief, 2001 (PDF; 2,5 MB).
- Tomas Akenine-Möller, Jacob Ström: Graphics for the Masses: A Hardware Rasterization Architecture for Mobile Phones. ACM Transactions on Graphics 22, 3 (Jul. 2003): 801–808
- Tomas Akenine-Moller: An Extremely Inexpensive Multisampling Scheme. Technical report, Chalmers University of Technology/Ericsson Mobile Platforms AB, Aug. 2003, S. 79 (PDF; 165 kB).
- Jon Hasselgren u. a.: A Family of Inexpensive Sampling Schemes. Computer Graphics Forum 24, 4 (Dec. 2005): 843–848
- Ares Lagae, Philip Dutré: A Comparison of Methods for Generating Poisson Disk Distributions.Report CW 459, Department of Computer Science, Katholieke Universiteit Leuven 2006 A Comparison of Methods for Generating Poisson Disk Distributions. Abgerufen am 13. Juli 2019.
- Turner Whitted: An Improved Illumination Model for Shaded Display. Communications of the ACM 23, 6 (June 1980): 343–349 (PDF; 4,6 MB)
- David Kirk, James Arvo: Unbiased Sampling Techniques for Image Synthesis. ACM SIGGRAPH Computer Graphics 25, 4 (July 1991): 153–156
- Manfred Ernst, Marc Stamminger, Gunther Greiner: Filter Importance Sampling. In: Proceedings IEEE Symposium on Interactive Ray Tracing 2006. ISBN 1-4244-0693-5, S. 125–132 (Filter Importance Sampling. Abgerufen am 13. Juli 2019.).
- Stephanie Winner u. a.: Hardware Accelerated Rendering Of Antialiasing Using A Modified A-buffer Algorithm. In: SIGGRAPH ’97 Proceedings. ACM Press, New York 1997, ISBN 0-89791-896-7, S. 307–316.
- Norman Jouppi, Chun-Fa Chang: Z³: An Economical Hardware Technique for High-Quality Antialiasing and Transparency. In: Proceedings of the Eurographics/SIGGRAPH Workshop on Graphics Hardware ’99. ACM, New York 1999, ISBN 1-58113-170-4, S. 85–93.
- Michael Deering, David Naegle: The SAGE Graphics Architecture. In SIGGRAPH ’02 Proceedings. ACM, New York 2002, ISBN 1-58113-521-1, S. 683–692 (PDF; 190 kB).
- http://msdn.microsoft.com/archive/default.asp?url=/archive/en-us/dx8_vb/directx_vb/graphics_using_3b8z.asp (Link nicht abrufbar)
- Fabio Policarpo, Francisco Fonseca: Deferred Shading Tutorial. (PDF; 1,5 MB (Memento vom 6. März 2009 im Internet Archive))
- Alexander Reshetov: Morphological Antialiasing. In: Proceedings of High Performance Graphics. ACM, New York 2009, ISBN 978-1-60558-603-8, S. 109–116 (PDF; 1,8 MB (Memento vom 20. August 2010 im Internet Archive)).