Fraktal

Fraktal ist ein vom Mathematiker Benoît Mandelbrot 1975 geprägter Begriff (lateinisch fractus ‚gebrochen‘, von lateinisch frangere‚ (in Stücke zer-)‚brechen‘), der bestimmte natürliche oder künstliche Gebilde oder geometrische Muster bezeichnet.

Berühmtes Fraktal:
die Mandelbrot-Menge (sogenanntes „Apfelmännchen“)

Diese Gebilde oder Muster besitzen im Allgemeinen keine ganzzahlige Hausdorff-Dimension, sondern eine gebrochene – daher der Name – und weisen zudem einen hohen Grad von Skaleninvarianz bzw. Selbstähnlichkeit auf. Das ist beispielsweise der Fall, wenn ein Objekt aus mehreren verkleinerten Kopien seiner selbst besteht. Geometrische Objekte dieser Art unterscheiden sich in wesentlichen Aspekten von gewöhnlichen glatten Figuren.

Begriff und Umfeld

Der Begriff Fraktal kann sowohl substantivisch als auch adjektivisch verwendet werden. Das Gebiet der Mathematik, in dem Fraktale und ihre Gesetzmäßigkeiten untersucht werden, heißt fraktale Geometrie und ragt in mehrere andere Bereiche hinein, wie Funktionentheorie, Berechenbarkeitstheorie und dynamische Systeme. Wie der Name schon andeutet, wird der klassische Begriff der euklidischen Geometrie erweitert, was sich auch in den gebrochenen und nicht natürlichen Dimensionen vieler Fraktale widerspiegelt. Neben Mandelbrot gehören Wacław Sierpiński und Gaston Maurice Julia zu den namensgebenden Mathematikern.

Beispiele

Julia-Menge für das quadratische Polynom f(z) = z² −0.4 + 0.6i in der zweidimensionalen komplexen Zahlenebene

Hilbert-Polygone in 7 Iterationen, dazu die Hilbert-Kurve

Die bekanntesten Fraktale sind in der gewöhnlichen zweidimensionalen euklidischen Ebene oder im dreidimensionalen euklidischen Raum definiert. Zu den bekanntesten Fraktalen gehören:

Die Mandelbrot-Menge ist als Teilmenge der Gaußschen Zahlenebene definiert.
Die Julia-Mengen sind verschiedenartige Mengen, die ebenfalls als Teilmenge der Gaußschen Zahlenebene definiert sind.
Die Schneeflockenkurve (Koch-Kurve) ist ein einfaches zweidimensionales Fraktal mit einfacheren und sehr interessanten Eigenschaften, das meistens anhand seiner Begrenzungslinie und einfachen Iterationsschritten definiert wird. In seiner vollständigen Variante ist es spiegelsymmetrisch, punktsymmetrisch und 6-zählig drehsymmetrisch.
Die Hilbert-Kurve ist eine spiegelsymmetrische und raumfüllende Kurve in der zweidimensionalen Ebene. Sie lässt sich problemlos auf höhere Dimensionen verallgemeinern.
Die Peano-Kurve ist eine punktsymmetrische und raumfüllende Kurve in der zweidimensionalen Ebene. Sie lässt sich problemlos auf höhere Dimensionen verallgemeinern.
Das Sierpinski-Dreieck wird mithilfe von selbstähnlichen Dreiecken in der zweidimensionalen Ebene definiert, die gleichseitige Dreiecke oder auch allgemeine Dreiecke sein können. Die dreidimensionale Variante ist das Sierpinski-Tetraeder. Wenig überraschend sind auch Verallgemeinerungen des Sierpinski-Dreiecks auf höhere Dimensionen möglich. Sie werden Sierpinski-Simplexe genannt.

Wegen ihrer angeblich höchst seltsamen Eigenschaften wurden fraktale Kurven früher auch Monsterkurven genannt.

Sierpinski-Dreieck in der 7. Iterationsstufe

Pythagoras-Baum

Menger-Schwamm nach der 4. Iterationsstufe

Die einfachsten Beispiele für selbstähnliche Objekte sind Strecken, Parallelogramme (zum Beispiel Quadrate) und Würfel, denn sie können durch zu ihren Seiten parallele Schnitte in verkleinerte Kopien ihrer selbst zerlegt werden. Diese sind jedoch keine Fraktale, weil ihre Ähnlichkeits-Dimension und ihre Lebesgue’sche Überdeckungsdimension übereinstimmen.

Die Selbstähnlichkeit muss nicht perfekt sein, wie die erfolgreiche Anwendung der Methoden der fraktalen Geometrie auf natürliche Gebilde wie Bäume, Wolken, Küstenlinien usw. zeigt. Die genannten Objekte sind in mehr oder weniger starkem Maß selbstähnlich strukturiert, denn ein Baumzweig sieht ungefähr so aus wie ein verkleinerter Baum, die Ähnlichkeit ist jedoch nicht streng, sondern stochastisch. Im Gegensatz zu Formen der euklidischen Geometrie, die bei einer Vergrößerung oft flacher und damit einfacher werden, z. B. ein Kreis, können bei Fraktalen immer komplexere und neue Details auftauchen.

Fraktale Muster werden oft durch rekursive Operationen erzeugt. Auch einfache Erzeugungsregeln ergeben nach wenigen Rekursionsschritten schon komplexe Muster.

Dies ist zum Beispiel am Pythagoras-Baum zu sehen. Ein solcher Baum ist ein Fraktal, welches aus Quadraten aufgebaut ist, die so angeordnet sind wie im Satz des Pythagoras definiert.

Ein weiteres Fraktal ist das Newton-Fraktal, erzeugt über das zur Nullstellenberechnung verwendete Newton-Verfahren.

Beispiele für Fraktale im dreidimensionalen Raum sind der Menger-Schwamm und die Sierpinski-Pyramide auf Basis des Tetraeders (so wie das Sierpinski-Dreieck auf dem gleichseitigen Dreieck basiert). Entsprechend lassen sich auch in höheren Dimensionen Fraktale nach Sierpinski bilden – bspw. basierend auf dem Pentachoron im vierdimensionalen Raum.

Fraktale Dimension und Selbstähnlichkeit

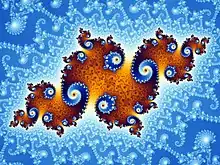
Ein kleiner Ausschnitt vom Rand der Mandelbrotmenge. Hier zeigt sie Ähnlichkeit mit einer Julia-Menge.

In der Mathematik ist die fraktale Dimension einer Menge eine Verallgemeinerung des Dimensionsbegriffs von geometrischen Objekten wie Kurven (eindimensional) und Flächen (zweidimensional), insbesondere bei Fraktalen. Das Besondere ist, dass die fraktale Dimension keine ganze Zahl sein muss. Es gibt unterschiedliche Möglichkeiten, eine fraktale Dimension zu definieren.

In der traditionellen Geometrie ist eine Linie eindimensional, eine Fläche zweidimensional und ein räumliches Gebilde dreidimensional. Für die fraktalen Mengen lässt sich die Dimensionalität nicht unmittelbar angeben: Führt man beispielsweise eine Rechenoperation für ein fraktales Linienmuster tausende von Malen fort, so füllt sich mit der Zeit die gesamte Zeichenfläche (etwa der Bildschirm des Computers) mit Linien, und das eindimensionale Gebilde nähert sich einem zweidimensionalen.

Mandelbrot benutzte den Begriff der verallgemeinerten Dimension nach Hausdorff und stellte fest, dass fraktale Gebilde meist eine nicht-ganzzahlige Dimension aufweisen. Sie wird auch als fraktale Dimension bezeichnet. Daher führte er folgende Definition ein:

Ein Fraktal ist eine Menge, deren Hausdorff-Dimension größer ist als ihre Lebesgue’sche Überdeckungsdimension.

Jede Menge mit nicht-ganzzahliger Dimension ist also ein Fraktal. Die Umkehrung gilt nicht, Fraktale können auch ganzzahlige Dimension besitzen, beispielsweise das Sierpinski-Tetraeder.

Besteht ein Fraktal aus einer bestimmten Anzahl von verkleinerten Kopien seiner selbst und ist dieser Verkleinerungsfaktor für alle Kopien derselbe, so verwendet man die Ähnlichkeits-Dimension $D$ , die in solchen einfachen Fällen mit der Hausdorff-Dimension übereinstimmt.

D={\frac {\log({\text{Anzahl selbstähnlicher Teile}})}{\log({\text{Verkleinerungsfaktor}})}}

Die Selbstähnlichkeit kann aber auch nur im statistischen Sinn bestehen. Man spricht dann von Zufallsfraktalen.

Selbstähnlichkeit, eventuell im statistischen Sinn, und zugehörige fraktale Dimensionen charakterisieren also ein fraktales System bzw. bei Wachstumsprozessen sogenanntes fraktales Wachstum, z. B. Diffusionsbegrenztes Wachstum.

Ein Beispiel für ein selbstähnliches Fraktal ist das Sierpinski-Dreieck, welches aus drei auf die halbe Seitenlänge verkleinerten Kopien seiner selbst aufgebaut ist. Es hat somit die Ähnlichkeits-Dimension ${\tfrac {\log 3}{\log 2}}\approx 1{,}585$ , während die Lebesgue’sche Überdeckungsdimension gleich 1 ist. Die Ähnlichkeits-Dimension ist ein Beispiel für die Definition einer fraktalen Dimension.

Anwendungen

Durch ihren Formenreichtum und den damit verbundenen ästhetischen Reiz spielen sie in der digitalen Kunst eine Rolle und haben dort das Genre der Fraktalkunst hervorgebracht. Ferner werden sie bei der computergestützten Simulation formenreicher Strukturen, beispielsweise realitätsnaher Landschaften, eingesetzt. Um in der Funktechnik verschiedene Frequenzbereiche zu empfangen, werden Fraktalantennen genutzt.

Fraktale in der Natur

Romanesco

Junger Wurmfarn: Hier ist die fraktale Struktur besonders gut erkennbar

Fraktale Erscheinungsformen findet man auch in der Natur. Dabei ist jedoch die Anzahl der Stufen von selbstähnlichen Strukturen begrenzt und beträgt oft nur drei bis fünf. Typische Beispiele aus der Biologie sind die fraktalen Strukturen bei der grünen Blumenkohlzüchtung Romanesco und bei den Farnen. Auch der Blumenkohl hat einen fraktalen Aufbau, wobei man es diesem Kohl auf den ersten Blick häufig gar nicht ansieht. Es gibt aber immer wieder einige Blumenkohlköpfe, die dem Romanesco im fraktalen Aufbau sehr ähnlich sehen.

Weit verbreitet sind fraktale Strukturen ohne strenge, aber mit statistischer Selbstähnlichkeit. Dazu zählen beispielsweise Bäume, Blutgefäße, Flusssysteme und Küstenlinien. Im Fall der Küstenlinie ergibt sich als Konsequenz die Unmöglichkeit einer exakten Bestimmung der Küstenlänge: Je genauer man die Feinheiten des Küstenverlaufes misst, umso größer ist die Länge, die man erhält. Im Falle eines mathematischen Fraktals, wie beispielsweise der Kochkurve, wäre sie unbegrenzt.

Fraktale finden sich auch als Erklärungsmodelle für chemische Reaktionen. Systeme wie die Oszillatoren (Standardbeispiel Belousov-Zhabotinsky-Reaktion) lassen sich einerseits als Prinzipbild verwenden, andererseits aber auch als Fraktale erklären. Ebenso findet man fraktale Strukturen auch im Kristallwachstum und bei der Entstehung von Mischungen, z. B. wenn man einen Tropfen Farblösung in ein Glas Wasser gibt. Die Lichtenberg-Figur zeigt ebenfalls fraktale Struktur.

Das Auffasern von Bast lässt sich über die fraktale Geometrie von Naturfaserfibrillen erklären. Insbesondere ist die Flachsfaser eine fraktale Faser.

Verfahren zur Erzeugung von Fraktalen

Fraktale können auf viele verschiedene Arten erzeugt werden, doch alle Verfahren enthalten ein rekursives Vorgehen:

Die Iteration von Funktionen ist die einfachste und bekannteste Art, Fraktale zu erzeugen; die Mandelbrot-Menge entsteht so. Eine besondere Form dieses Verfahrens sind IFS-Fraktale (Iterierte Funktionensysteme), bei denen mehrere Funktionen kombiniert werden. So lassen sich natürliche Gebilde erstellen.
Dynamische Systeme erzeugen fraktale Gebilde, sogenannte seltsame Attraktoren.
L-Systeme, die auf wiederholter Textersetzung beruhen, eignen sich gut zur Modellierung natürlicher Gebilde wie Pflanzen und Zellstrukturen.

Es gibt fertige Programme, sogenannte Fraktalgeneratoren, mit denen Computeranwender auch ohne Kenntnis der mathematischen Grundlagen und Verfahren Fraktale darstellen lassen können.

Einfache und regelmäßige Fraktale mit Abbildungen

Fraktal	L-System	Winkel	Strecken-Verhältnis	Visualisierung	Anzahl der Spiegelachsen	Punktsymmetrie	Drehsymmetrie	Dimensionen	Hausdorff-Dimension des Randes
Drachenkurve	F → R oder F → L R → +R--L+ L → -R++L-	$45^{\circ }$	$1:1/{\sqrt {2}}$	Drachenkurve	0	nein	keine	2
Gosper-Kurve	F → R oder F → L R → R+L++L-R--RR-L+ L → -R+LL++L+R--R-L	$60^{\circ }$	$1:1/{\sqrt {7}}$	Gosper-Kurve	0	ja	6-zählig	2
Hilbert-Kurve	X X → -YF+XFX+FY- Y → +XF-YFY-FX+	$90^{\circ }$	$1:1/2$	Hilbert-Kurve	1	nein	keine	2
Koch-Flocke	F--F--F F → F+F--F+F	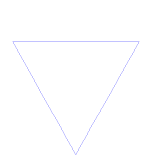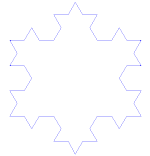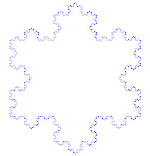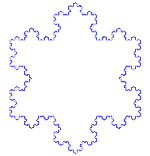$60^{\circ }$	$1:1/3$		12	ja	6-zählig	2	${\frac {\log(4)}{\log(3)}}\approx 1{,}262$
Peano-Kurve	X X → XFYFX+F+YFXFY-F-XFYFX Y → YFXFY-F-XFYFX+F+YFXFY	$90^{\circ }$		Peano-Kurve	0	ja	2-zählig	2
Peano-Kurve	F F → F-F+F+F+F-F-F-F+F	$90^{\circ }$	$1:1/3$	Peano-Kurve	0	ja	2-zählig	2
Penta Plexity	F++F++F++F++F F → F++F++F\|F-F++F	$36^{\circ }$	$1:1/\left({\frac {{\sqrt {5}}+1}{2}}\right)^{2}$	Penta Plexity	10	nein	5-zählig	2
Pfeilspitze	F → R oder F → L R → -L+R+L- L → +R-L-R+	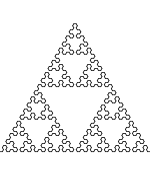$60^{\circ }$	$1:1/2$	Pfeilspitzen-Fraktal	1	nein	keine	2
Sierpinski-Dreieck	FXF--FF--FF X → --FXF++FXF++FXF-- F → FF	$60^{\circ }$			6	nein	3-zählig	2	${\frac {\log(3)}{\log(2)}}\approx 1{,}585$
Sierpinski-Dreieck, 2. Variante	F--F--F F → F--F--F--ff f → ff	$60^{\circ }$	$1:1/3$	Sierpinski-Dreieck	6	nein	3-zählig	2	${\frac {\log(3)}{\log(2)}}\approx 1{,}585$
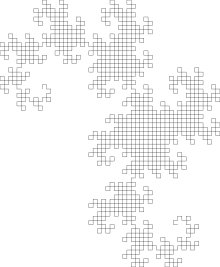
Sierpinski-Teppich	F F → F+F-F-FF-F-F-fF f → fff	$90^{\circ }$	$1:1/3$	Sierpinski-Teppich	8	ja	4-zählig	2
Lévy-C-Kurve	F F → +F--F+	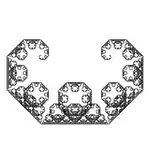$45^{\circ }$	$1:1/{\sqrt {2}}$	C-Kurve	1	nein	keine	2	$\approx 1{,}9340$

Erklärung des L-Systems

Das optionale, also nicht notwendige F wird im Allgemeinen als Strecke benutzt, die durch eine Anweisungsfolge ersetzt wird. Wie das F stehen auch andere groß geschriebene Buchstaben wie R und L für einen Streckenabschnitt, der ersetzt wird. + und − stehen für einen bestimmten Winkel, der im Uhrzeigersinn oder gegen den Uhrzeigersinn läuft. Das Symbol | bezeichnet eine Kehrtwendung des Zeichenstiftes, also eine Drehung um 180°. Gegebenenfalls setzt man dafür ein entsprechendes Vielfaches des Drehwinkels ein.

Beispiel Drachenkurve

 F → R
 R → +R--L+
 L → -R++L-

F ist eine einfache Strecke zwischen zwei Punkten. F → R heißt, dass die Strecke F durch R ersetzt wird. Dieser Schritt ist notwendig, da es zwei rekursive Ersetzungen R und L besitzt, die sich gegenseitig enthalten. Im Weiteren wird wie folgt ersetzt:

 R
 +R--L+
 +(+R--L+)--(-R++L-)+
 +(+(+R--L+)--(-R++L-)+)--(-(+R--L+)++(-R++L-)-)+
 .
 .
 .

Ab einem bestimmten Abschnitt muss dieser Ersetzungsprozess abgebrochen werden, um eine Grafik zu bekommen:

 +(+(+r--l+)--(-r++l-)+)--(-(+r--l+)++(-r++l-)-)+

Dabei stellen r und l jeweils eine fest vorgegebene Strecke dar.

Zufallsfraktale

Daneben spielen in der Natur auch „Zufallsfraktale“ eine große Rolle. Diese werden nach probabilistischen Regeln erzeugt. Dies kann etwa durch Wachstumsprozesse geschehen, wobei man beispielsweise diffusionsbegrenztes Wachstum (Witten und Sander) und „Tumorwachstum“ unterscheidet. Im ersten Fall entstehen baumartige Strukturen, im letzten Fall Strukturen mit runder Form, je nachdem, in welcher Weise man die neu hinzukommenden Teilchen an die schon vorhandenen Aggregate anlagert. Wenn die fraktalen Exponenten nicht konstant sind, sondern z. B. von der Entfernung von einem zentralen Punkt des Aggregats abhängen, spricht man von sog. Multifraktalen.[1]

Siehe auch

Burning ship (Fraktal)

Literatur

Julia-Menge

Reinhart Behr: Fraktale, Formen aus Mathematik und Natur. Klett-Schulbuchverlag, 1. Auflage, Stuttgart (1993), ISBN 3-12-722420-6.
Reinhart Behr: Ein Weg zur fraktalen Geometrie. Klett-Schulbuchverlag, 1. Auflage, Stuttgart (1989), ISBN 3-12-722410-9.
Julius Dufner, Frank Unseld, Andreas Roser: Fraktale und Julia-Mengen. Verlag Harri Deutsch (1998), Thun, ISBN 3-8171-1564-4
Gerald Edgar: Measure, Topology, and Fractal Geometry. Verlag Springer (2008), New York, ISBN 978-0-387-74748-4
Kenneth Falconer: Fractal Geometry. Mathematical Foundations and Applications, 3. Auflage, John Wiley & Sons, Ltd., Chichester (2014), ISBN 978-1-119-94239-9
Horst Halling, Rolf Möller: Mathematik fürs Auge – Eine Einführung in die Welt der Fraktale, Spektrum 1995, ISBN 3-86025-427-8.
Gilbert Helmberg: Getting Acquainted with Fractals, Walter de Gruyter 2007, ISBN 978-3-11-019092-2.
Jürgen Kriz: Chaos und Struktur. Systemtheorie Band 1. Quintessenz, München, Berlin 1992, ISBN 3-928036-69-6.
Benoît B. Mandelbrot: Les Objects Fractals: Forme, Hasard et Dimension, 1975 (französisch). In Englisch: Fractals: Form, Chance and Dimension, W.H. Freeman & Co, 1977, ISBN 0-7167-0473-0.
Benoît B. Mandelbrot: Die fraktale Geometrie der Natur, Birkhäuser 1987, ISBN 3-7643-2646-8 (engl. 1982 publiziert).
Heinz-Otto Peitgen, Peter H. Richter: The Beauty of Fractals. Images of Complex Dynamical Systems, Springer 1986, ISBN 0-387-15851-0 bzw. ISBN 3-540-15851-0
Heinz-Otto Peitgen, Dietmar Saupe: The Science of Fractal Images, Springer 1st ed. 1988, ISBN 0-387-96608-0
Herbert Voß: Chaos und Fraktale selbst programmieren, franzis 1994, ISBN 3-7723-7003-9
Herbert Zeitler, Dušan Pagon[A 1] : Fraktale Geometrie – Eine Einführung. Für Studienanfänger, Studierende des Lehramtes, Lehrer und Schüler. Braunschweig / Wiesbaden, Vieweg 2000, ISBN 3-528-03152-2

Anmerkungen

Pagon ist ein slowenischer Mathematiker und Professor an der Universität Maribor. Vgl. Artikel über Dušan Pagon in der slowenischen Wikipedia!

Einzelnachweise

Siehe z. B. Z. Eisler, J. Kertész: Multifractal model of asset returns with leverage effect. In: Physica A: Statistical Mechanics and its Applications. 343, November 2004, S. 603–622. arxiv:cond-mat/0403767. doi:10.1016/j.physa.2004.05.061.

Weblinks

Commons: Fraktal – Album mit Bildern, Videos und Audiodateien

Wiktionary: Fraktal – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Website über Fraktale für Einsteiger mit zahlreichen Illustrationen
Natürliche Fraktale in Wissenschaft und Medizin (englisch)
GNU Xaos, freier interaktiver Fraktal Explorer
Online CGI Mandelbrot Fractal Explorer – Interaktive Erforschung der Mandelbrot-Menge mit MapClient (OpenLayers)
Video vergrößern Mandelbox – Beispiel für 3D-Fraktal
Flug durch ein animiertes 3D Fraktal (Video)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[2] Pagon ist ein slowenischer Mathematiker und Professor an der Universität Maribor. Vgl. Artikel über Dušan Pagon in der slowenischen Wikipedia!

[1] Siehe z. B. Z. Eisler, J. Kertész: Multifractal model of asset returns with leverage effect. In: Physica A: Statistical Mechanics and its Applications. 343, November 2004, S. 603–622. arxiv:cond-mat/0403767. doi:10.1016/j.physa.2004.05.061.