Bildsynthese
Bildsynthese oder Rendern (von englisch (to) render, deutsch etwas erbringen, herausgeben, leisten) bezeichnet in der Computergrafik die Erzeugung eines Bildes aus Rohdaten. Rohdaten können geometrische Beschreibungen im 2D- oder 3D-Raum (auch Szene genannt), HTML, SVG etc. sein.
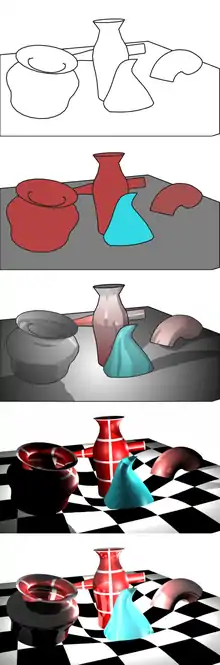
Eine Szene ist ein virtuelles räumliches Modell, das Objekte und deren Materialeigenschaften, Lichtquellen, sowie die Position und Blickrichtung eines Betrachters definiert.
Computerprogramme zum Rendern von Bildern werden Renderer genannt. Unterschieden werden z. B. die Rendering Engine für Computerspiele, die HTML-Renderer etc.
Beim Rendern müssen üblicherweise folgende Aufgaben gelöst werden:
- die Ermittlung der vom virtuellen Betrachter aus sichtbaren Objekte (Verdeckungsberechnung)
- die Simulation des Aussehens von Oberflächen, beeinflusst durch deren Materialeigenschaften (Shading)
- die Berechnung der Lichtverteilung innerhalb der Szene, die sich unter anderem durch die indirekte Beleuchtung zwischen Körpern äußert.
Daneben erfordert die Erzeugung von Computeranimationen einige zusätzliche Techniken. Ein wichtiger Einsatzbereich ist die interaktive Synthese von Bildern in Echtzeit, bei der meist Hardwarebeschleunigung zum Einsatz kommt. Bei der realistischen Bildsynthese hingegen wird auf hohe Bildqualität oder physikalische Korrektheit Wert gelegt, während die benötigte Rechenzeit eine untergeordnete Rolle spielt.
Echtzeitrendern
Beim Echtzeitrendern wird eine Reihe von Bildern schnell berechnet und die zugrundeliegende Szene vom Anwender interaktiv verändert. Die Berechnung erfolgt ausreichend schnell, so dass die Bildfolge als dynamischer Prozess empfunden wird. Ab einer Bildfrequenz von etwa 6 fps ist eine interaktive Benutzung möglich, bei 15 fps lässt sich mit Sicherheit von Echtzeit sprechen.[1] Auf modernen Computern wird das Echtzeitrendern durch Hardwarebeschleunigung mittels Grafikkarten unterstützt. Mit wenigen Ausnahmen unterstützt Grafikhardware nur Punkte, Linien und Dreiecke als grafische Grundobjekte.[2]
Grafikpipeline
Beim Echtzeitrendern beschreibt die Grafikpipeline den Weg von der Szene bis zum fertigen Bild. Es handelt sich um eine Modellvorstellung, die je nach System variieren kann. Die Grafikpipeline ist oftmals in Teilen ähnlich wie Prozessorpipelines implementiert, bei denen Berechnungen parallel ausgeführt werden. Eine Grafikpipeline kann in drei große Schritte aufgeteilt werden: Anwendung, Geometrie und Rasterung.[3]
Der Anwendungsschritt nimmt alle Änderungen an der Szene vor, die vom Anwender im Rahmen der Interaktion festgelegt werden, und gibt sie an den nächsten Schritt der Pipeline weiter. Daneben kommen hier Techniken wie Kollisionserkennung, Animation, Morphing und Beschleunigungsverfahren mittels räumlicher Unterteilungsschemata zum Einsatz.
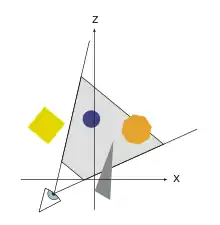
Der Geometrieschritt übernimmt einen Großteil der Operationen mit den Vertices, den Eckpunkten der Grundobjekte. Er lässt sich in verschiedene Unterschritte aufteilen, die nacheinander Transformationen in verschiedene Koordinatensysteme vornehmen. Um die perspektivische Abbildung zu vereinfachen, arbeiten fast alle geometrischen Operationen des Geometrieschrittes mit homogenen Koordinaten. Dabei werden Punkte durch vier Koordinaten und Transformationen durch 4×4-Matrizen definiert.
Zunächst werden alle Grundobjekte der Szene so transformiert, dass der virtuelle Beobachter entlang der z- (Tiefen-)achse blickt. Falls die Szene Lichtquellen enthält, wird für jeden Vertex anhand der Materialeigenschaften des entsprechenden Dreiecks eine Farbe berechnet. Das vom Betrachter aus sichtbare Volumen der Szene ist ein Pyramidenstumpf (Frustum). Im nächsten Schritt wird dieses Frustum in einen Würfel transformiert, was einer Zentralprojektion entspricht. Teilweise oder vollständig außerhalb des Sichtvolumens liegende Grundobjekte werden mittels Clipping- und Culling-Techniken beschnitten oder entfernt. Schließlich wird eine Transformation angewandt, die die Vertex-Koordinaten an den gewünschten Zeichenbereich des Bildschirms verschiebt. Die z-Koordinaten bleiben dabei weiter erhalten, da sie für die spätere Verdeckungsberechnung benötigt werden.
Im Rasterungsschritt werden alle verbleibenden, projizierten Grundobjekte gerastert, indem die zu ihnen gehörenden Pixel eingefärbt werden. Da bei überlappenden Dreiecken nur die sichtbaren Teile angezeigt werden sollen, wird ein Z-Buffer verwendet, der die Verdeckungsberechnung übernimmt.
Grafik-APIs
Zur Ansteuerung von Grafikpipelines werden üblicherweise Grafik-APIs verwendet, die die Grafikhardware abstrahieren und dem Programmierer viele Aufgaben abnehmen. Wesentlich zur Entwicklung des Echtzeitrenderns hat der ursprünglich von Silicon Graphics eingeführte Standard OpenGL beigetragen. Die aktuellen Neuerungen von OpenGL und Microsofts DirectX finden hauptsächlich in modernen Computerspielen ihre Anwendung. Außer DirectX und OpenGL gab es noch andere Ansätze, wie zum Beispiel Glide, die sich allerdings nicht durchsetzen konnten. Im professionellen Bereich hat OpenGL große Bedeutung. DirectX ist hingegen stark auf die Entwicklung von Spielen optimiert. DirectX ist eine proprietäre Software, die nur unter Windows verfügbar ist; sie ist kein offener Standard.
Historische Techniken
- Siehe auch Geschichte der Computergrafik
Die erste interaktive Technik zur Verdeckungsberechnung wurde 1969 von Schumacker und anderen veröffentlicht.[4] Schumackers Algorithmus[5] diente der Flugsimulation für die US-Streitkräfte, eine Anwendung, bei der stets massiv in Grafikhardware investiert wurde.
In der Frühzeit der Computerspiele mit interaktiver 3D-Grafik wurden alle rechenaufwändigen Grafikoperationen noch vom Hauptprozessor des Rechners übernommen. Daher konnten nur sehr einfache und eingeschränkte Renderverfahren genutzt werden. Der Ego-Shooter Wolfenstein 3D (1992) etwa verwendete zur Verdeckungsberechnung Raycasting, womit sich nur eine festgelegte Höhendimension und rechtwinklig aneinandergrenzende Räume darstellen ließen. Doom kombinierte Raycasting mit zweidimensionalem Binary Space Partitioning, um die Effizienz zusätzlich zu steigern und komplexere Szenen rendern zu können.
Shading und direkte Beleuchtung
Als Shading (dt.: Schattierung) wird allgemein die Berechnung der Farben an Oberflächen anhand der zugehörigen Materialeigenschaften und dem direkt von den Lichtquellen eintreffenden Licht bezeichnet. Das Shading kommt sowohl beim Echtzeitrendern als auch beim realistischen Rendern zum Einsatz. Die indirekte Beleuchtung von anderen Oberflächen bleibt dabei zunächst unberücksichtigt. Einen Spezialfall stellen nichtfotorealistische Shading-Techniken (Non-photorealistic Rendering) dar, bei denen zum Beispiel aus ästhetischen Gründen Verfremdungen erzeugt werden, etwa Cel Shading für comicähnliche Bilder.
Lichtquellen und Schatten
Bei der Modellierung sind verschiedene, oft physikalisch nicht korrekte Arten von Lichtquellen üblich. Directional Lights senden parallele Lichtstrahlen ohne Abschwächung in eine bestimmte Richtung, Punktlichtquellen emittieren Licht in alle Richtungen, und Spot Lights emittieren Licht nur in einem kegelförmigen Bereich. In Wirklichkeit besitzen Lichter eine bestimmte Fläche; die Lichtintensität nimmt quadratisch mit der Entfernung ab. Dies wird bei der realistischen Bildsynthese berücksichtigt, während beim Echtzeitrendern meistens nur einfache Lichtquellen verwendet werden.
Schatten sind ein wichtiges Element von Computergrafiken, da sie dem Anwender Rückschlüsse über die Platzierung von Objekten im Raum geben. Weil Lichtquellen eine bestimmte Größe haben, wirken Schatten in Wirklichkeit mehr oder weniger verschwommen. Dies wird bei realistischen Renderverfahren berücksichtigt.
Lokale Beleuchtungsmodelle
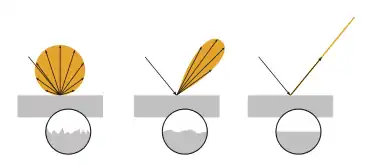
Lokale Beleuchtungsmodelle beschreiben das Verhalten von Licht auf Oberflächen. Wenn ein Lichtteilchen auf einen Körper trifft, wird es entweder reflektiert, absorbiert oder – außer bei Metallen – ins Innere des Körpers gebrochen. Nur auf ganz glatten Oberflächen wird eintreffendes Licht gespiegelt; bei nichtmetallischen Körpern wird der relative Anteil des reflektierten und gebrochenen Lichtes durch die fresnelschen Formeln beschrieben.
Mikroskopische Unebenheiten führen dazu, dass das Licht nicht gespiegelt wird, sondern mit einer bestimmten Wahrscheinlichkeit in eine davon abweichende Richtung reflektiert wird. Die Wahrscheinlichkeitsverteilung, die dieses Verhalten für ein Material beschreibt, wird bidirektionale Reflektanzverteilungsfunktion (BRDF) genannt. Lokale Beleuchtungsmodelle sind meist parametrierbare BRDFs. Ideal diffuse Oberflächen lassen beispielsweise mit dem lambertschen Gesetz und glänzende Oberflächen mit den Phong-Beleuchtungsmodell simulieren. Beim Echtzeitrendern wird oft eine Kombination aus einem diffusen, einem glänzenden und einem konstanten Faktor verwendet. Für die realistische Bildsynthese wurden weitere, physikalisch plausiblere Modelle entwickelt.
Die BRDF geht davon aus, dass das an einem Punkt der Oberfläche eintreffende Licht auch genau dort wieder austritt. In Wirklichkeit streuen nichtmetallische Körper Licht in ihrem Inneren, wodurch sich ein weicheres Erscheinungsbild ergibt. Die Simulation dieser Volumenstreuung ist vor allem für die realistische Bildsynthese von Bedeutung.
Interpoliertes Shading

Beim Echtzeitrendern gibt es drei übliche Methoden, um die Beleuchtung eines Dreiecks zu berechnen. Beim Flat Shading wird die Farbe für ein Dreieck berechnet und das gesamte Dreieck mit dieser Farbe gefüllt. Dadurch werden die Facetten, aus denen sich das Modell zusammensetzt, deutlich sichtbar. Das von den meisten Grafikkarten unterstützte Gouraud Shading hingegen bestimmt die Farbe an jedem Eckpunkt eines Dreiecks, sodass bei der Rasterung zwischen diesen Farbwerten interpoliert wird und sich ein weicheres Erscheinungsbild als beim Flat Shading ergibt. Beim Phong Shading ist zusammen mit jedem Vertex die Normale an diesem Vertex verfügbar. Bei der Rasterung wird zwischen den Normalen interpoliert und das lokale Beleuchtungsmodell entsprechend dieser Normalen berechnet. Dieses Verfahren vermeidet einige Darstellungsprobleme des Gouraud Shading.
Mapping-Techniken


Im Normalfall werden lokale Beleuchtungsmodelle einheitlich auf ein gesamtes Objekt angewandt. Mapping-Techniken dienen der Simulation von Oberflächendetails aufgrund von Farb- oder Strukturvariationen. Dabei werden die Material- oder Geometrieeigenschaften an jedem Punkt der Oberfläche anhand einer Funktion oder Rastergrafik variiert. Viele Mapping-Techniken werden auch von Grafikhardware unterstützt. Neben den im Folgenden aufgeführten Verfahren wurden viele weitere Mapping-Techniken entwickelt.
- Texture Mapping ist die älteste Mapping-Technik und dient dazu, ein zweidimensionales Bild (Textur) auf einer Oberfläche abzubilden oder sie damit zu „bekleben“. Neben Rastergrafiken werden auch prozedurale Texturen verwendet, bei denen die Farbe an einem Punkt durch eine mathematische Funktion bestimmt wird. Bei der Bestimmung eines Farbwertes sind verschiedene Filtermethoden möglich. Auf Grafikhardware ist Mip Mapping gebräuchlich, bei dem aus Effizienzgründen die Textur in verschiedenen Bildauflösungen vorliegt.
- Bumpmapping dient der Simulation von Oberflächenunebenheiten. Dabei werden die tatsächlichen Normalenvektoren an der Oberfläche durch eine Bump Map gestört. Die Geometrie eines Objekts wird dadurch allerdings nicht beeinflusst.
- Displacement Mapping dient ebenfalls der Simulation von Oberflächenunebenheiten, im Gegensatz zu Bump Mapping wird jedoch die Oberflächengeometrie tatsächlich verändert. Da dafür meist nicht ausreichend Vertices zur Verfügung stehen, werden zusätzliche Oberflächenpunkte eingefügt, die entsprechend einem Höhenfeld verschoben werden.
- Environment Mapping oder Reflection Mapping dient der Simulation von Spiegelungseffekten beim Echtzeitrendern. Dazu wird vom Betrachter ein Strahl zum reflektierenden Objekt ausgesendet und reflektiert. Im Gegensatz zum Raytracing (siehe unten) wird nicht der Schnittpunkt des reflektierten Strahls mit der am nächsten liegenden Oberfläche berechnet. Stattdessen wird anhand der Richtung des Strahls der Farbwert aus einem vorausberechneten Bild der Szene ermittelt.
Realistisches Rendern und globale Beleuchtung
Wie realistisch ein gerendertes Bild wirkt, hängt maßgeblich davon ab, inwieweit die Verteilung des Lichts innerhalb der Szene berechnet wurde. Während beim Shading nur die direkte Beleuchtung berechnet wird, spielt bei der indirekten Beleuchtung die Reflexion von Licht zwischen Objekten eine Rolle. Dadurch werden Effekte wie Räume, die nur durch einen schmalen Lichtspalt insgesamt erhellt werden, möglich. Die Lichtpfadnotation wird dazu verwendet, um die Fähigkeiten eines Renderalgorithmus bezüglich der Simulation der Beleuchtung anzugeben. Werden alle Arten der Lichtreflexion berücksichtigt, so spricht man von globaler Beleuchtung. Sie muss für ein realistisches Ergebnis berücksichtigt werden und ist bei Echtzeitverfahren nicht oder nur sehr eingeschränkt möglich.
Mathematisch wird die globale Beleuchtung durch die Rendergleichung beschrieben, die anhand von radiometrischen Größen angibt, wie viel Licht einen Oberflächenpunkt von einem anderen Oberflächenpunkt aus nach einer Reflexion erreicht. Die Rendergleichung lässt sich mit Raytracing, für Spezialfälle auch mit Radiosity berechnen. Neben diesen beiden großen Techniken zur realistischen Bildsynthese werden, vor allem in der Filmtechnik, Varianten des REYES-Systems verwendet.
Raytracing
Raytracing ist in erster Linie ein Algorithmus zur Verdeckungsberechnung, der auf der perspektivischen Aussendung von Strahlen vom Beobachter aus basiert. Jeder Strahl wird gegen alle Grundobjekte auf einen Schnittpunkt getestet und gegebenenfalls die Entfernung zu diesen Objekten berechnet. Das sichtbare Objekt ist dasjenige mit der geringsten Entfernung. In erweiterten Formen kann Raytracing auch Lichtreflexionen und -brechungen simulieren.
Um die globale Beleuchtung mittels Raytracing zu berechnen, muss die an diesem Pixel eintreffende „Lichtstärke“ mit Hilfe der Rendergleichung ermittelt werden. Dies geschieht mittels einer Monte-Carlo-Simulation, bei der viele Lichtstrahlen zufällig an den Oberflächen ausgesandt werden. Derartige Raytracing-Techniken nennt man Monte-Carlo-Raytracing; das einfachste dieser Verfahren ist Path Tracing. Diese Algorithmen sind vergleichsweise zeitaufwändig, bei Szenen mit komplizierten Lichtverhältnissen und unterschiedlichen Materialien jedoch die einzige Möglichkeit. Bei geeigneter Implementierung liefern sie außerdem erwartungstreue Bilder. Das bedeutet, dass das Bildrauschen die einzige Abweichung zur korrekten, vollständig konvergierten Lösung darstellt. Photon Mapping wird dazu eingesetzt, die Berechnung der Lichtverteilung mittels Raytracing zu beschleunigen, kann aber zu sichtbaren Bildfehlern (Artefakten) führen.
Radiosity

Der Radiosity-Algorithmus ist in seiner Grundform nur auf ideal diffuse Flächen anwendbar und basiert auf der Unterteilung der Oberflächen in kleine Teilflächen (Patches). Unter diesen Voraussetzungen lässt sich mit den Rendergleichungen für jeden Patch ein lineares Gleichungssystem aufstellen, das numerisch gelöst wird; Radiosity gehört damit zu den Finite-Elemente-Methoden. Radiosity lässt sich zwar auf beliebige Materialien erweitern, die Präzision ist jedoch durch die Zahl der Patches und die resultierenden Speicheranforderungen begrenzt. Ein Vorteil gegenüber Raytracing ist, dass die Lichtverteilung blickpunktunabhängig berechnet wird und die Verdeckungsberechnung nicht Teil des eigentlichen Radiosity-Algorithmus ist. Dadurch eignet sich Radiosity besonders zum Rendern statischer oder wenig animierter Szenen in Echtzeit, sofern eine zeitaufwändige Vorausberechnung vertretbar ist.
Volumengrafik
Bei der Volumengrafik werden die zu rendernden Objekte nicht als Oberflächen beschrieben, sondern als räumliche Datensätze in Form von Voxelgittern. Voxelgitter enthalten gitterförmig angeordnete Werte, die die „Dichte“ eines Objektes beschreiben. Diese Form der Datenrepräsentation ist besonders geeignet für Objekte, die keine klaren Umrisse haben, etwa Wolken. Zum Rendern von Voxelgittern sind besondere Techniken erforderlich. Da zahlreiche bildgebende Verfahren Voxeldaten erzeugen, ist die Volumengrafik auch für die Medizin von Bedeutung.
Literatur
- Tomas Akenine-Möller, Eric Haines: Real-Time Rendering. AK Peters, Natick, Mass. 2002, ISBN 15-6881-182-9 (Webseite)
- Philip Dutré u. a.: Advanced Global Illumination. AK Peters, Natick, Mass. 2003, ISBN 15-6881-177-2 (Webseite)
- Andrew Glassner: Principles of Digital Image Synthesis. Morgan Kaufmann, London 1995, ISBN 15-5860-276-3
- Matt Pharr, Greg Humphreys: Physically Based Rendering. From Theory to Implementation. Morgan Kaufmann, London 2004, ISBN 01-2553-180-X (Webseite)
- Ian Stephenson: Production Rendering: Design and Implementation. Springer, London 2005, ISBN 1-85233-821-0
- Alan Watt: 3D Computer Graphics. Addison-Wesley, Harlow 2000, ISBN 0-201-39855-9
Weblinks
Einzelnachweise
- Tomas Akenine-Möller, Eric Haines: Real-Time Rendering, S. 1
- Tomas Akenine-Möller, Eric Haines: Real-Time Rendering, S. 7
- Tomas Akenine-Möller, Eric Haines: Real-Time Rendering, S. 11
- Ivan Sutherland u. a.: A Characterization of Ten Hidden-Surface Algorithms. ACM Computing Surveys (CSUR) 6, 1 (March 1974): 1–55, hier S. 23, ISSN 0360-0300
- R. A. Schumaker u. a.: Study for Applying Computer-Generated Images to Visual Simulation. AFHRL-TR-69-14. US Air Force Human Resources Laboratory, 1969