Geometrische Optik
Die geometrische Optik oder Strahlenoptik bedient sich des Strahlenmodells des Lichtes[1] und behandelt damit auf einfache, rein geometrische Weise den Weg des Lichtes auf Linien.[2]
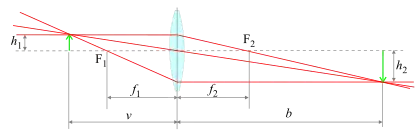
Das Modell eines auf einer Linie begrenzten Lichtstrahls entspricht nicht der physikalischen Realität,[2] einen solchen Lichtstrahl kann man folglich auch nicht experimentell realisieren.[1] Dennoch lässt sich mit Hilfe der Strahlenoptik die optische Abbildung, die Hauptthema der technischen Optik ist,[3] oft mit ausreichender Genauigkeit beschreiben.[4]
Beschränkt man die geometrische Optik auf Strahlen, die die optische Achse sehr flach schneiden, liegt die sogenannte paraxiale Optik vor. Dafür lassen sich geschlossene mathematische Ausdrücke für Abbildungsgleichungen finden. Man wendet diese Methode aber hauptsächlich nur dann an, wenn man sich einen schnellen grundsätzlichen Überblick verschaffen will, bevor man umfangreiche Ermittlungen genauer durchführt.[5]
Die geometrische Optik lässt sich mathematisch als Grenzfall der Wellenoptik für verschwindend kleine Wellenlängen des Lichts auffassen. Sie versagt aber auch in diesem Fall, wenn die Verhältnisse für Strahlen mit hoher Energiedichte oder nahe an der Grenze zum Schatten (kein Licht) untersucht werden sollen.[1]
Axiome der geometrischen Optik
Als allgemeinste Grundlage der Strahlenoptik lässt sich das Fermatsche Prinzip ansehen.[6] Es führt auf die beiden ersten der folgenden Axiome.[6]
- 1. Axiom: In homogenem Material sind die Lichtstrahlen gerade.
- 2. Axiom: An der Grenze zwischen zwei homogenen isotropen Materialien wird das Licht im Allgemeinen nach dem Reflexionsgesetz reflektiert und nach dem Brechungsgesetz gebrochen.
- 3. Axiom: Der Strahlengang ist umkehrbar; bei Umkehrung der Richtung eines Strahls ändert sich sein Verlauf nicht.
- 4. Axiom: Die Lichtstrahlen durchkreuzen einander, ohne sich gegenseitig zu beeinflussen.
Anwendungen
Hauptanwendungsgebiet der Strahlenoptik ist die Behandlung der Abbildung durch optische Elemente, Geräte und Systeme, wie Linsen, Brillen, Objektive, Fernrohre und Mikroskope.
Auch das Raytracing-Verfahren in der 3D-Computergrafik beruht auf den Gesetzen der geometrischen Optik.
Die Luftspiegelungen durch eine heiße Luftschicht über sonnenbeschienenem Asphalt und andere Naturphänomene können auch durch Anwendung dieses Prinzips erklärt werden.
Grenzen
Effekte, die von der geometrischen Optik nicht beschrieben werden können, sind unter anderem:
- die Beugung, die das Auflösungsvermögen optischer Instrumente begrenzt. Sie kann nur im Rahmen der Wellenlehre oder der Quantenmechanik verstanden werden.
- die Interferenz, die ebenfalls durch die Wellenlehre oder Quantenmechanik erfassbar ist, und die z. B. für die Wirkungsweise der Antireflexbeschichtung von wesentlicher Bedeutung ist.
- die Polarisation, die quantenmechanisch mit dem Spin der Photonen zu tun hat, aber auch mit der Wellenlehre erklärbar ist. Sie ist im Zusammenhang mit der Doppelbrechung von Bedeutung, und auch für die teilweise Reflexion an brechenden Flächen, wo sie die Quantität des reflektierten Lichts beeinflusst, siehe Fresnelsche Formeln oder Brewster-Winkel.
- die Absorption und die Streuung des Lichts.
Einige Methoden der geometrischen Optik, insbesondere die Matrizenoptik, übertragen sich jedoch auf das Konzept der Gaußstrahlen, welches die Effekte der Wellenoptik teilweise mit berücksichtigt.
Weiterführendes
- Einführung in die Strahlenoptik Ausführliche Seite über Strahlenoptik mit vielen Beispielen, Bildern und Experimenten
Einzelnachweise
- Heinz Haferkorn: Optik. Physikalisch-technische Grundlagen und Anwendungen. 3., bearbeitete und erweiterte Auflage. Barth, Leipzig u. a. 1994, ISBN 3-335-00363-2, S. 35.
- Heinz Haferkorn: Optik. Physikalisch-technische Grundlagen und Anwendungen. 3., bearbeitete und erweiterte Auflage. Barth, Leipzig u. a. 1994, ISBN 3-335-00363-2, S. 11.
- Heinz Haferkorn: Optik. Physikalisch-technische Grundlagen und Anwendungen. 3., bearbeitete und erweiterte Auflage. Barth, Leipzig u. a. 1994, ISBN 3-335-00363-2, S. 157.
- Heinz Haferkorn: Optik. Physikalisch-technische Grundlagen und Anwendungen. 3., bearbeitete und erweiterte Auflage. Barth, Leipzig u. a. 1994, ISBN 3-335-00363-2, S. 180.
- Heinz Haferkorn: Optik. Physikalisch-technische Grundlagen und Anwendungen. 3., bearbeitete und erweiterte Auflage. Barth, Leipzig u. a. 1994, ISBN 3-335-00363-2, S. 184.
- Heinz Haferkorn: Optik. Physikalisch-technische Grundlagen und Anwendungen. 3., bearbeitete und erweiterte Auflage. Barth, Leipzig u. a. 1994, ISBN 3-335-00363-2, S. 37.