Computeranimation
Computeranimation bezeichnet die computergestützte Erzeugung von Animationen. Sie verwendet die Mittel der Computergrafik und ergänzt sie um zusätzliche Techniken.
Manchmal wird zwischen computergestützter und computergenerierter Animation unterschieden. Während erstere sich auf digitalisierte Zeichnungen stützt, zwischen denen die Animationssoftware interpoliert, um flüssige Bewegungsabläufe zu erhalten, arbeitet letztere mit einer dreidimensionalen Szene, aus der mit den Mitteln der Bildsynthese direkt Bilder erzeugt werden.
3D-Animation
3D-Animation wird unter anderem für Computerspiele, Animationsfilme und die lebensechte Rekonstruktion von ausgestorbenen Tieren verwendet. Die Animationen sind vor allem zum Darstellen digitaler Personen und Charaktere von Bedeutung.
Ein Animator verwendet eine digitale Marionette, um den Charakter zu positionieren, und verwendet dann ein System von Bewegungspfaden oder Splines, um die Bewegung des Charakters zwischen diesen Positionen zu definieren.
3D-Animation ist ein technisch intensiver Prozess, bei dem häufig viele Spezialisten den Charakter modellieren, mit Knochen und Steuerelementen ausrüsten, animieren und dann für die endgültige Ausgabe texturieren und beleuchten. Charaktere werden in 3D-Animationen in einem Computerprogramm digital modelliert und dann mit einem „Skelett“ versehen, mit dem Animatoren die Modelle bewegen können.
Die Animation erfolgt durch Positionieren der Modelle auf bestimmten Keyframes. Anschließend berechnet der Computer eine Interpolation zwischen diesen Einzelbildern, um eine Bewegung zu erzeugen. Wenn die Modellierung oder Animation abgeschlossen ist, rendert der Computer jedes Bild einzeln, was je nach Qualität der benötigten Bilder sehr zeitaufwändig sein kann. Ein 3D-Animator verbringt die meiste Zeit damit, Kurven zu betrachten, die die Bewegung verschiedener Körperteile im Laufe der Zeit darstellen. Im Gegensatz zur herkömmlichen Animation sollten die Körperteile des Charakters immer vorhanden sein und berücksichtigt werden.[1]
Schlüsselbilder und Interpolation

Die Technik der Schlüsselbildanimation (Keyframing) stammt ursprünglich aus der Produktion von Zeichentrickfilmen. Dabei werden nicht alle Einzelbilder von Hand gezeichnet, sondern nur sogenannte Schlüsselbilder, die grob den Bewegungsablauf vorgeben. Die Einzelbilder zwischen den Schlüsselbildern werden durch Interpolationstechniken automatisch berechnet, dies nennt man auch Tweening.
Bei computergenerierten Animationen ist der Begriff „Schlüsselbild“ insofern irreführend, als die Interpolation nicht anhand der vollständigen Bilder erfolgt. Stattdessen werden verschiedene Parameter der Szene gesetzt, etwa die Positionen der Objektmittelpunkte, ihre Farben und Skalierung, die Kameraposition und -blickrichtung oder die Intensität der Lichtquellen. Für unterschiedliche Parameter können auch unterschiedliche Schlüsselbilder gewählt werden.
Interpolationsmethoden
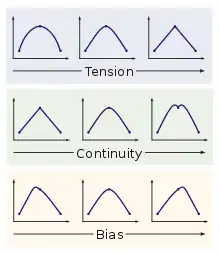
Um plötzliche Geschwindigkeitsänderungen zu vermeiden, wird die Interpolationskurve der Schlüsselwerte meist so gewählt, dass ihre Ableitung stetig ist. Eine höhere stetige Differenzierbarkeit ist üblicherweise nicht nötig, da die zweite Ableitung (Beschleunigung) sich auch in der Natur oft abrupt ändert. Diese Eigenschaften machen Catmull-Rom-Splines zu einer guten Wahl für Animationskurven. Viele Animationssysteme erlauben dem Animator, durch gezielte Anpassung der Tangenten an den Schlüsselwerten die Animationskurve fein abzustimmen. Dies geschieht oft durch Kontrolle von Tension, Continuity und Bias (TCB). Dazu werden die Catmull-Rom- zu Kochanek-Bartels-Splines erweitert, mit denen diese drei Parameter für jeden Schlüsselwert eingestellt werden können.
Wenn ein Bewegungspfad durch Digitalisierung gewonnen wurde, so muss er vor seiner Verwendung erst geglättet werden, um Sprünge und Rauschen zu entfernen.
Kurvenparametrisierung
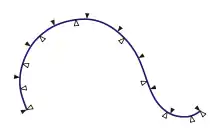
Die bloße Beschreibung der Animationskurve ist im Allgemeinen nicht ausreichend, wenn nicht nur die Position, sondern auch die Geschwindigkeit eines Objekts entlang eines Pfades kontrolliert werden soll. Das liegt daran, dass durch die Anpassung einer Kurve an mehrere Punkte nichts über die Geschwindigkeit zwischen diesen Punkten ausgesagt wird. Die Parametrisierung der üblicherweise zur Animation verwendeten Kurventypen stimmt nicht mit der tatsächlichen Distanz entlang einer Kurve überein.
Eine Möglichkeit, die Geschwindigkeit eines Objektes zu kontrollieren, besteht darin, den Animator eine zusätzliche Distanz-Zeit-Funktion bestimmen zu lassen, die angibt, wie weit sich ein Objekt zu einem bestimmten Zeitpunkt entlang der Kurve bewegt haben soll. Ebenfalls möglich sind Geschwindigkeit-Zeit- oder sogar Beschleunigung-Zeit-Funktionen. In jedem Fall muss das Animationsprogramm intern die Kurvenlänge entlang einer Animationskurve in deren Parameterdarstellung umwandeln. Für die meisten Spline-Typen gibt es dazu keine analytische Formel, sodass Näherungsverfahren wie das Newtonverfahren angewandt werden müssen.
Das häufigste Geschwindigkeitsprofil in der Animation ist Ease-in/Ease-out. Dabei beschleunigt ein Objekt vom Startpunkt aus, erreicht eine Höchstgeschwindigkeit, und bremst schließlich bis zum Endpunkt wieder ab. Dieses Verhalten kann durch ein Segment der Sinusfunktion modelliert werden.
Rotationen
Die Rotation ist neben der Verschiebung die einzige Transformation, die die Form eines Objektes beibehält; sie spielt daher bei der Animation starrer Körper eine große Rolle. Zur Interpolation von dreidimensionalen Rotationen werden besondere Methoden verwendet. Eine einfache Art, die Rotation eines Objektes anzugeben, ist mittels eulerscher Winkel. Wenn diese Winkel animiert werden, kann das Gimbal-Lock-Problem auftreten. Dieser Effekt entsteht, wenn eine der drei Rotationsachsen mit einer anderen zusammenfällt, wodurch ein Freiheitsgrad verloren geht.
Um dieses Problem zu umgehen, werden in der Computeranimation Quaternionen zur Formulierung von Rotationen verwendet. Quaternionen bilden einen vierdimensionalen Raum, für den Operationen wie Addition und Multiplikation definiert sind. Um einen Punkt zu rotieren, wird er zunächst als Quaternion dargestellt, die Rotation im Quaternion-Raum angewandt, und wieder in die üblichen kartesischen Koordinaten umgewandelt. Aufeinanderfolgende Rotationen im Quaternion-Raum entsprechen Produkten von Quaternionen. Rotationen werden meistens durch Einheitsquaternionen ausgedrückt, die man sich als Punkte auf einer vierdimensionalen Einheitssphäre vorstellen kann. Die Interpolation auf der vierdimensionalen Einheitssphäre wird auch Slerp genannt. Da sie mathematisch sehr aufwändig ist, wird oft nur linear zwischen Quaternionen interpoliert. Die Zwischenschritte werden anschließend normalisiert, um sie wieder auf die vierdimensionale Einheitssphäre zu projizieren. Gleichmäßigere Resultate lassen sich erreichen, indem der De-Casteljau-Algorithmus angewandt wird, sodass mehrfache lineare Interpolationen ausgeführt werden.
Soll ein Objekt einem Bewegungspfad folgen, so wird oft erwartet, dass es nicht nur verschoben wird, sondern auch, dass seine Orientation dem Pfad folgt. Die Beziehung zwischen der Orientation eines Objekts und den Kurveneigenschaften kann durch die frenetschen Formeln ausgedrückt werden. Dabei müssen einige Spezialfälle beachtet werden, in denen die Formeln nicht angewandt werden können, etwa bei Kurvenabschnitten ohne Krümmung. Falls die Kamera bewegt werden soll, so wird oft ein Center of interest angegeben, das stets im Zentrum des Bildes liegen soll. Das Animationsprogramm ändert dann die Orientation der Kamera entsprechend.
Hierarchische Objekte
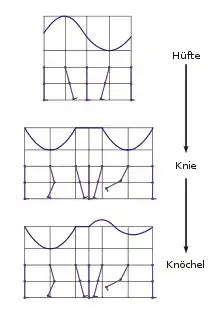
Objekte sind oft hierarchisch modelliert, sodass die Randbedingungen bezüglich Verbundenheit oder relativer Platzierung in einer baumartigen Struktur organisiert sind. Ein Beispiel für ein hierarchisches Modell ist ein Planetensystem, in dem Monde um Planeten und diese wiederum um die Sonne rotieren. Maschinenteile oder Figuren sind aus zusammenhängenden Objekten aufgebaut, die untereinander mit diversen Gelenktypen wie Schub- und Drehgelenken verbunden sind. Derartige hierarchisch aufgebaute Objekte werden im Englischen Articulated Structures genannt. In der Computeranimation derartiger Modelle wird zum Teil auf die kinematischen Techniken der Robotik zurückgegriffen. Für die Character animation sind diese Techniken jedoch nicht ausreichend, da sich Figuren auf freiere, komplexere und geschicktere Weise bewegen als Roboter. Ein weiterer Grund ist, dass die Gelenke von Tieren selbst verformbar sind und somit nicht mit den üblichen Methoden modelliert werden können.
Eine direkte, vergleichsweise mühsame Methode zur Animation von kinematischen Ketten oder zusammenhängenden Strukturen nutzt die direkte Kinematik. Um eine bestimmte Bewegung zu definieren, beginnt der Animator an der Wurzel der Hierarchie und fährt mit den Unterknoten fort, wobei er jedes Mal das Animationsskript ändert. So wird bei der Animation eines Beines zunächst die zeitliche Änderung der Rotation am Hüftgelenk vorgegeben, was in einem plumpen Schritt resultiert. Anschließend wird das Kniegelenk und schließlich der Fußknöchel animiert. Selbst dieses einfache Beispiel ist mit Problemen behaftet, so etwa wird die vertikale Verschiebung der Hüfte während der Bewegung nicht berücksichtigt.
Die inverse Kinematik arbeitet auf höherer Ebene. Hierbei wird nur die Bewegung der Endpunkte einer Struktur manuell definiert. Die Animationssoftware berechnet dann automatisch das Verhalten der übrigen Gelenke, um diese Bewegung auszuführen. Je komplizierter eine Struktur ist, desto schwieriger werden diese Berechnungen. Ein weiteres Problem der inversen Kinematik ist, dass sie dem Animator kaum Spielraum lässt.
Für die Animation der Dinosaurier im Film Jurassic Park (1993) wurde direkte Kinematik verwendet, wobei jedoch die Bewegungsabläufe in Stop-Motion-Manier von echten Modellen mit Sensoren ermittelt wurden. Eine weitere Möglichkeit ist Motion Capture, bei der die Bewegungen eines Darstellers mittels Sensoren oder Marker auf dessen Körper erfasst werden. Außerdem gibt es noch rein synthetisch berechnete Modelle, die mit virtuellen Knochen und Muskeln realistische Bewegungen erzeugen.
Kollisionserkennung
Die Kollisionserkennung ist ein unverzichtbares Hilfsmittel, wenn mehr als ein Objekt animiert werden soll. Dabei werden in einem ersten Schritt die Objekte ermittelt, die miteinander kollidieren, und in einem zweiten Schritt die genauen Kollisionspunkte berechnet. In ihrer naiven Form hat die Kollisionserkennung in Abhängigkeit von der Anzahl der berücksichtigten Objekte quadratische Laufzeit. Der Prozess kann erheblich beschleunigt werden, indem Objekte in Bounding Volumes gepackt werden, zwischen denen ein schnellerer Test auf Überlappung möglich ist. Wenn die Bounding Volumes einander nicht überlappen, so tun dies auch die enthaltenen Objekte nicht. Wenn ja, müssen die enthaltenen Objekte direkt gegeneinander getestet werden. Die Körper, die die Objekte umschließen, können auch hierarchisch strukturiert werden.
Eine weitere Möglichkeit zur Beschleunigung beruht auf der Erkenntnis, dass die Kollisionserkennung in gleichen Zeitabständen verschwenderisch ist. Stattdessen sollte sie zu Zeitpunkten durchgeführt werden, deren Häufigkeitsverteilung proportional zur Wahrscheinlichkeit des Auftretens von Kollisionen ist. Ein weiteres Problem ist, dass die Kollisionserkennung zu einem Zeitpunkt einsetzen kann, bei dem vor allem schnell bewegte Objekte bereits ein Stück ineinander eingedrungen sind. Dieser Effekt muss nachträglich korrigiert werden, etwa indem der Weg der Objekte entlang des Bewegungspfads zurückberechnet wird.
Die Kollisionserkennung kann verschiedenen Anwendungen dienen, zum Beispiel um den Weg eines Objekts unter Vermeidung von Kollisionen zu berechnen. Physikalisch lässt sich eine Kollision als elastischer oder plastischer Stoß beschreiben und die weitere Bewegung der Objekte entsprechend berechnen.
Gruppensimulation

Um das Verhalten mehrerer Objekte mit den Mitteln der Gruppensimulation zu bestimmen, kann der Animator Techniken der künstlichen Intelligenz verwenden. Dadurch plant jedes der Objekte die Bewegungen, die einem festgelegten Plan entsprechen, und führt sie aus. Viele Computerspiele verwenden derartige autonome Objekte, um intelligente Gegner oder Verbündete des Spielers zu erzeugen. Es stellt sich heraus, dass eine einzelne Figur umso weniger Intelligenz aufweisen muss, je größer die Gruppe ist. Bei hunderten von Figuren entsteht ein Schwarmverhalten, bei dem die Bewegung jeder Figur – hier oft Boid genannt – auf einfache Weise von nur wenigen Nachbarn beeinflusst wird. Kollisionsvermeidung ist eines der Ergebnisse eines solchen Verhaltens.
Eine wesentlich einfachere, aber dennoch nützliche Technik zur Kontrolle von Objektgruppen sind Partikelsysteme. Die Anzahl der verwendeten, oft sehr kleinen Partikel ist üblicherweise erheblich größer als bei Schwarmanimationen und kann viele Tausend erreichen. Die genaue Anzahl der Partikel kann außerdem während der Animation schwanken, da bei jedem Schritt neue Partikel entstehen und alte gelöscht werden können. Dies ist einer der Gründe warum z. B. Flüssigkeitssimulationen wie RealFlow für jedes zu rendernde Bild ein neues 3D-Modell erzeugen. Die Bewegung einzelner Partikel folgt oft den Gesetzen der Mechanik. Zu den Anwendungen von Partikelsystemen zählen die Animation von Explosionen, spritzenden Flüssigkeiten, Rauch, Feuer oder Erscheinungen ohne feste Begrenzung. Um ein plausibleres Erscheinungsbild zu gewährleisten, können die Bewegung und andere Parameter der Partikel zufällig verändert werden. Das Verhalten eines Partikelsystems wird normalerweise bestimmt, indem Kräfte im Raum festgelegt werden. So kann zum Beispiel ein Partikel in eine neue Richtung „geblasen“ werden, sobald es einen bestimmten Ort erreicht, von einem „Gravitationszentrum“ angezogen oder die eigentlich fertiggestellte Simulation wie ein normales 3D-Modell verformt werden.
Mit physikalisch basierten Simulationen lassen sich meist wesentlich realistischere Animationen als mit Partikelsystemen erzeugen. Beispiele sind die Animation von Flüssigkeiten, Feuer, Rauch oder flexiblen Stofftüchern. Hierzu müssen die Differentialgleichungen, die diese Erscheinungen beschreiben, mit den Mitteln der numerischen Mathematik gelöst werden.
Literatur
- Rick Parent: Computer Animation: Algorithms and Techniques. Morgan Kaufmann, Amsterdam 2008, ISBN 978-0-12-532000-9
Weblinks
- Hinweis: Durch die zahlreichen animierten Grafiken in dieser Kategorie sind sehr hohe Ladezeiten möglich.