Orbitalflug
Ein Orbitalflug oder orbitaler Raumflug ist der Flug eines Raumflugkörpers in einer Umlaufbahn („Orbit“) um einen Himmelskörper. Orbitalflüge sind zu unterscheiden von Suborbitalflügen, die zwar den Weltraum erreichen, aber zu langsam sind, um eine Umlaufbahn zu erreichen.[1]

Das Adjektiv orbital, insbesondere in Abgrenzung zum Adjektiv suborbital, kann sich außer auf Raumflüge und Missionen auch auf entsprechende Raketen, Nutzlasten, Raketenstarts, Startrampen und Weiteres beziehen.
Himmelskörper und die erste kosmische Geschwindigkeit
Umlaufbahnen sind grundsätzlich um jeden beliebigen Himmelskörper möglich, also etwa um Sterne, Planeten, Monde, Asteroiden oder Kometen. Wegen der Größe des Universums beschränkt sich die menschliche Raumfahrt jedoch bisher auf das Sonnensystem, und der weitaus häufigste Himmelskörper für Orbitalflüge ist die Erde.
Um nach einem Start auf der Oberfläche eines Himmelskörpers in einer Umlaufbahn zu fliegen, muss der Raumflugkörper nicht nur den Weltraum erreichen, sondern auch auf eine bestimmte Geschwindigkeit in horizontaler Richtung beschleunigt werden, die sogenannte erste kosmische Geschwindigkeit oder Kreisbahngeschwindigkeit. Bei der Erde beträgt diese in einem niedrigstmöglichen Orbit rund 7,9 km/s, also mehr als 28.000 km/h.[2] Das ist mit Raketentriebwerken möglich. Weltraumschleudern sind bisher nur Zukunftsvisionen.
Die Kreisbahngeschwindigkeit ist von der Flughöhe abhängig. In größerer Höhe ist sie niedriger. Ein geostationärer Satellit hat beispielsweise nur eine Geschwindigkeit von rund 3 km/s, das sind rund 11.000 km/h.
Ein Flugkörper, der von weiter weg zunehmend in den gravitativen Einflussbereich eines Himmelskörpers gerät, kann durch geeignetes Abbremsen auf eine Relativgeschwindigkeit, die unter der Fluchtgeschwindigkeit seiner aktuellen Höhe liegt, in eine Umlaufbahn um den Himmelskörper einschwenken.
Umlaufbahn

Der Flugkörper durchläuft ohne Antrieb und Reibung immer wieder dieselbe Ellipsenbahn
Allgemeines
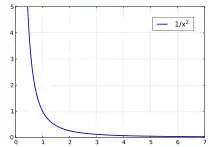
Die entscheidende Kraft für Flugkörper auf Umlaufbahnen um einen Himmelskörper ist die Gravitation. Sie wirkt stets in Richtung des Massenmittelpunkts des Himmelskörpers und ihre Größe ist umgekehrt proportional zum Quadrat des Abstands. Im Verhältnis zur Masse von Himmelskörpern ist die Masse eines Flugkörpers vernachlässigbar klein. Auch andere Himmelskörper können im einfachsten Fall näherungsweise vernachlässigt werden. Damit vereinfacht sich das Zweikörperproblem zu einem Einkörperproblem. Dessen Lösung wurde erstmals Anfang des 17. Jahrhunderts von Johannes Kepler in Form der drei Keplerschen Gesetze formuliert. Das Gravitationsgesetz von Isaac Newton erklärt die beobachteten Umlaufbahnen als Wirkung der Gravitationskraft. Eine andere, für extrem hohe Massedichten und Geschwindigkeiten bessere Beschreibung der Gravitation liefert die von Albert Einstein entwickelte allgemeine Relativitätstheorie.
Eigenschaften einer Umlaufbahn
Nach der klassischen Physik ist jede Umlaufbahn im allgemeinen Fall eine geschlossene elliptische Bahn (Trajektorie), bei der sich der Massenmittelpunkt des Himmelskörpers in einem Brennpunkt der Ellipse befindet. Man nennt sie auch eine Keplerellipse. Als Sonderfall kann die Ellipse auch ein Kreis sein.[3] Egal wie sie im Raum ausgerichtet ist, liegen alle Punkte der Umlaufbahn stets in einer Ebene, die deshalb auch Bahnebene oder Orbitalebene genannt wird. Sobald sich der Raumflugkörper in einer Umlaufbahn befindet, kann er dort prinzipiell ohne weiteren Antrieb verbleiben und auf ihr den Himmelskörper umkreisen.
Die Bahn und die Bewegung des Flugkörpers, relativ zum als ruhend angenommenen Bezugssystem des Himmelskörpers, werden durch verschiedene Bahnelemente beschrieben. Mit der Vis-Viva-Gleichung lässt sich die Momentangeschwindigkeit des Flugkörpers berechnen.[4] Sie hängt nur von der Masse des Himmelskörpers und vom Abstand des Flugkörpers zum Massenmittelpunkt des Himmelskörpers ab. Die Umlaufzeit hängt nur von der Masse des Himmelskörpers und der großen Halbachse der Bahn ab. Die Geschwindigkeit und die Umlaufzeit sind von der Masse des Flugkörpers unabhängig.
Für den häufigsten Fall, eine Umlaufbahn um die Erde, setzt normalerweise eine Rakete den Raumflugkörper an oder in der Nähe der Periapsis aus, dem erdnächsten Punkt der Ellipsenbahn. Wird dem Flugkörper dort eine höhere Geschwindigkeit als die Kreisbahngeschwindigkeit mitgegeben, so erreicht er auf der entgegengesetzten Seite die Apoapsis, den erdfernsten Punkt der Ellipsenbahn. Bei der Annäherung an die Apoapsis wird er langsamer. Anschließend „fällt“ er auf seiner Umlaufbahn weiter um den Himmelskörper herum, während seine Geschwindigkeit wieder zunimmt. Schließlich erreicht er erneut den Punkt seiner Periapsis mit der gleichen Geschwindigkeit und Flugrichtung wie zuvor. Auf diese Weise wird die gleiche Ellipsenbahn immer wieder zyklisch durchlaufen, ohne dass hierfür Energie benötigt wird oder verlorengeht.
Je schneller der Flugkörper an der Periapsis ist, desto exzentrischer ist die Ellipse und desto höher ist die Apoapsis. Bei einer Beschleunigung auf die Fluchtgeschwindigkeit – die im Fall der Erde auch die „zweite kosmische Geschwindigkeit“ genannt wird – weitet sich die Ellipse ins Unendliche zu einer Parabel aus. Die Fluchtgeschwindigkeit in einer gegebenen Höhe ist das -Fache der dortigen Kreisbahngeschwindigkeit. Mit noch höheren Geschwindigkeiten wird aus der Parabel eine Hyperbel. Der Flugkörper kann auf einer solchen Fluchtbahn dem Himmelskörper entfliehen.
Eigenbewegungen des Himmelskörpers, wie die Bewegung der Erde um die Sonne im Lauf eines Jahres, macht der orbitierende Körper, etwa ein Erdsatellit, „mit“, da er die gleichen gravitativen Einflüsse auch selbst erfährt. Seine Umlaufbahn ist bezogen auf den Massenmittelpunkt des Himmelskörpers fix. Die Ausrichtung der Bahnellipse – die Richtung der Apsidenlinie – wäre in Abwesenheit von Störungen und nach rein newtonscher Mechanik auch prinzipiell fix, bezogen auf das Universum (etwa weit entfernte Fixsterne). Sie kann jedoch bestimmte Störungen erfahren, siehe Apsidendrehung.
Bahnradius vs. Höhe
Der Bahnradius eines Körpers auf einer Umlaufbahn gibt seinen Abstand zum Massenmittelpunkt des umkreisten Himmelskörpers an, die (Flug-)Höhe hingegen seinen Abstand zur Oberfläche des Himmelskörpers. Beide Angaben werden in der Raumfahrt verwendet und sind nicht deckungsgleich, da sie sich um den Radius des – hier als kugelförmig angenommenen – Himmelskörpers unterscheiden, sie können jedoch leicht verwechselt werden. Sofern die Umlaufbahn keine Kreisbahn ist, schwanken der Bahnradius und die (Flug-)Höhe zyklisch zwischen dem Punkt der geringsten und der größten Entfernung.
Rotation
Die Rotation des Himmelskörpers ist für die Bahn und die Bewegung des orbitierenden Körpers im Weltraum prinzipiell irrelevant. Die senkrecht zur Rotationsachse stehende Äquatorebene spielt aber als wichtige Bezugsebene für die Bahnelemente eine Rolle – eine „äquatoriale“ Umlaufbahn verläuft deckungsgleich zu dieser Ebene und eine „polare“ Umlaufbahn im rechten Winkel zu ihr; andere Umlaufbahnen sind in einem bestimmten Winkel geneigt. Außerdem ist die Erdrotation für den Start von Erdsatelliten relevant, wo man sie zum Einsparen von Treibstoff nutzen kann, und spielt eine wichtige Rolle für die Bodenspur.
Auch der Raumflugkörper kann in seiner Umlaufbahn rotieren. Im Fall einer gebundenen Rotation ist seine Rotation mit seiner Umlaufperiode gekoppelt – zum Beispiel derart, dass der Raumflugkörper dem Himmelskörper stets die gleiche Seite zuweist.
Bahnstörungen
Perfekte elliptische Umlaufbahnen gibt es nur für den Fall, dass der gravitative Einfluss anderer Himmelskörper vernachlässigbar ist. Prinzipiell wirkt die Gravitationskraft unbegrenzt weit, so dass theoretisch jeder Himmelskörper im gesamten sichtbaren Universum einen Störeinfluss auf jede Flugbahn hat. Allerdings bedeutet der quadratische Abfall der Gravitationskraft verbunden mit den sehr großen Entfernungen zwischen den Himmelskörpern, dass der Störeinfluss vernachlässigt werden kann, solange der Flugkörper relativ nah am umkreisten Himmelskörper und relativ weit vom anderen Himmelskörper entfernt ist. Mit zunehmender Entfernung vom umkreisten Himmelskörper werden die Bahnstörungen stärker. In einer höheren Erdumlaufbahn verursachen vor allem die Sonne und ggf. der Mond spürbare Bahnstörungen.
Wenn man zwei einander umkreisende Himmelskörper betrachtet – etwa die Sonne und die Erde, oder die Erde und den Mond –, hat jeder der beiden Himmelskörper einen etwa kugelförmigen Raum, innerhalb dessen seine Gravitationskraft stärker ist als die des anderen Himmelskörpers. Dieser Raum wird die Hill-Sphäre genannt und nur innerhalb der Hill-Sphäre kann ein Flugkörper eine stabile Umlaufbahn haben. Für Flugbahnberechnungen verwendet man in der Praxis oft das Konzept der Einflusssphäre, die für jeden Himmelskörper eine bestimmte Distanz angibt, innerhalb derer sein Einfluss nicht ignoriert werden darf und deshalb in die Berechnung aufgenommen werden muss.
Auch relativistische Effekte, Unregelmäßigkeiten im Schwerefeld, atmosphärische Störeinflüsse und viele weitere Faktoren können zu Bahnstörungen führen. Je nach Fall müssen solche Bahnstörungen vorab berechnet, gemessen, und/oder es muss den Störungen eventuell durch Korrekturmanöver entgegengewirkt werden.
Orbitale Manöver
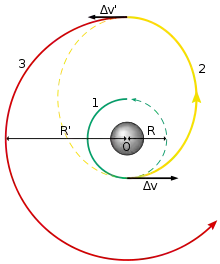
und sind die aus zwei Kraftstößen sich jeweils ergebenden Geschwindigkeitsänderungen des Flugkörpers.
Falls der Raumflugkörper über (Raketen-)Triebwerke verfügt, kann die Umlaufbahn mit Flugmanövern gezielt verändert werden. Triebwerke erzeugen mit Kraftstößen (im Englischen kick oder burn genannt) Schub (Englisch: thrust), der die Geschwindigkeit und ggf. auch die Bewegungsrichtung verändert. Da Treibstoff in der Raumfahrt stets ein knappes Gut ist, werden alle orbitalen Manöver auf ein notwendiges Minimum reduziert und in der Regel so treibstoffsparend wie möglich ausgeführt.
Vorwärtsgerichtete (prograde) bzw. rückwärtsgerichtete (retrograde) Kraftstöße heben alle Punkte der Bahn an bzw. senken alle Punkte der Bahn ab, bis auf denjenigen Punkt, an dem der Kraftstoß erfolgte. Am stärksten wird dabei der gegenüberliegende Bahnpunkt verändert. Wenn kein weiterer Kraftstoß erfolgt, erreicht der Flugkörper nach einer vollen Umkreisung auf der neuen Bahn stets wieder genau jenen Bahnpunkt, an dem der letzte Kraftstoß erfolgt war. Diese Eigenschaft folgt aus dem Ersten Keplerschen Gesetz.
- Um die Apoapsis anzuheben oder abzusenken, verwendet man einen Kraftstoß an der Periapsis. Dabei bleibt die Periapsis unverändert.
- Um die Periapsis anzuheben oder abzusenken, verwendet man einen Kraftstoß an der Apoapsis. Dabei bleibt die Apoapsis unverändert.
Um sowohl die Apoapsis als auch die Periapsis zu ändern, braucht man mindestens zwei Kraftstöße an gegenüberliegenden Bahnpunkten. Mit bestimmten Transferbahnen (etwa dem Hohmann-Transfer oder dem bi-elliptischen Transfer) können solche Manöver energetisch optimiert werden.
Eine weitere bemerkenswerte und „unintuitive“ Eigenschaft von orbitalen Manövern ist, dass ein vorwärtsgerichteter, somit momentan beschleunigender, Kraftstoß den Flugkörper auf seiner Bahn insgesamt verlangsamt, denn durch das Anheben der Bahn wird die durchschnittliche Geschwindigkeit niedriger und die Umlaufzeit länger. Umgekehrt wirkt ein rückwärtsgerichteter, somit momentan bremsender, Kraftstoß insgesamt beschleunigend, denn durch das Absenken der Bahn wird die durchschnittliche Geschwindigkeit höher und die Umlaufzeit kürzer.
Bei den bisher beschriebenen Manövern bleibt die Orbitalebene unverändert. Deren Bahnneigung (Inklination) kann mit quergerichteten Kraftstößen verändert werden. Diese müssen dafür an einem der beiden Knoten der bisherigen Bahn mit der gewünschten neuen Bahn erfolgen. Änderungen der Bahnneigung kosten allerdings verhältnismäßig viel Treibstoff. Deshalb werden Raumflugkörper bereits beim Start so nahe wie möglich an der gewünschten Orbitalebene gestartet und die Neigung wird danach maximal um wenige Grad verändert. Wegen seiner Nähe zum Äquator ist das Raumfahrtzentrum Guayana beispielsweise besonders gut geeignet, um geostationäre Satelliten zu starten.
Orbitalflüge um die Erde
Orbitalflüge um die Erde sind für alle Bereiche der Raumfahrt wichtig – von kommerziellen Anwendungen über militärische und wissenschaftliche. Mit Orbitalflügen werden beispielsweise Satelliten in Umlaufbahnen gebracht. Sie sind jedoch wesentlich aufwändiger und teurer als suborbitale Flüge mit der gleichen Nutzlast.[5] Falls eine unversehrte Rückkehr der Nutzlast zur Erde gewünscht ist, etwa bei bemannten Flügen, ist dies mit weiteren großen technischen Herausforderungen und Kosten verbunden.
Orbitalflüge um die Erde haben sogenannte geozentrische Umlaufbahnen. (Der Begriff „Erdumlaufbahn“ ist doppeldeutig und wird daher besser vermieden.) Raumflugkörper, die die Erde umkreisen, werden meist (Erd)satelliten genannt. Die Begriffe Orbiter oder Raumsonde verwendet man für sie nicht. Weltraumteleskope und Raumstationen auf Erdumlaufbahnen gehören ebenfalls zu den Satelliten. Der erdnächste bzw. der erdfernste Punkt der Bahn wird Perigäum bzw. Apogäum genannt.
Definitionen
Per Definition spricht man von einem Erdorbitalflug, wenn sich der Raumflugkörper auf einer Bahn befindet, deren Perigäum im Weltraum liegt, also höher als die Erdatmosphäre ist. Die Fédération Aéronautique Internationale (FAI) definiert die Grenze zum Weltraum bei 100 Kilometern über dem Meeresspiegel. Davon abweichend definieren die US-amerikanische NASA und die US Air Force bereits die Höhe von 50 Meilen (circa 80 km) als Beginn des Weltraums. Da Erdorbitalflüge typischerweise in Höhen von mehr als 200 Kilometern stattfinden, spielt die unterschiedliche Definition meist keine Rolle.
Der Unterschied zwischen suborbitalen und orbitalen Flügen kann auch für den Begriff „Raumfahrer“ von Bedeutung sein, je nachdem, welche Organisation den Begriff verwendet. Die Association of Space Explorers erkennt beispielsweise nur solche Personen als Raumfahrer an, die einen Orbitalflug absolviert und dabei mindestens einmal die Erde umkreist haben. Dieser Definition haben sich bis heute alle staatlichen Raumfahrtagenturen angeschlossen. Demnach betrachten sie Teilnehmer an suborbitalen Raumflügen nicht als Raumfahrer.
Raketen für Erdorbitalstarts

Raketen, die eine Nutzlast in eine Erdumlaufbahn befördern können, werden Orbitalraketen genannt.[6] In der Praxis benötigt man dazu mehrstufige Trägerraketen, denn mit einer einstufigen Rakete lässt sich die erste kosmische Geschwindigkeit nicht erreichen. Mit der Raketengrundgleichung kann die Beschleunigung von Raketen berechnet werden. Beim Start einer Rakete, bis ihre Oberstufe die Umlaufbahn erreicht, muss sie außer der reinen Beschleunigung auf die Kreisbahngeschwindigkeit auch noch Arbeit gegen die Anziehungskraft der Erde aufbringen. Dies wird als Gravitationsverlust bezeichnet. Zusätzlich kommt noch die Überwindung der Luftreibung hinzu.
Für Start- und orbitale Manöver eines Raumfahrzeugs bezeichnet man die benötigte und die verfügbare Fähigkeit zur Änderung der Geschwindigkeit mit Delta v. Die Masse des Raumfahrzeugs wirkt sich reduzierend auf sein verfügbares Delta v aus. Daher gilt insbesondere für die Nutzlast stets eine strenge Massenobergrenze. Zur Verringerung der Gesamtmasse werden Booster, leere Tanks und/oder Raketenstufen nach dem Ausbrennen abgetrennt, was das verfügbare Delta v für den Rest der Rakete erhöht. Durch Leichtbau lassen sich außerdem die mögliche Nutzlast erhöhen und Treibstoff einsparen.[7]
Die meisten heute gebauten Trägerraketen können nur einmal gestartet werden. Ihre abgetrennten Booster fallen zur Erde zurück, ihre abgetrennten Raketenstufen werden meist beim Wiedereintritt in der Atmosphäre zerstört und ihre Oberstufen verbleiben in der Regel funktionslos als Weltraummüll im Erdorbit. Es gibt aber auch teilweise wiederverwendbare Trägerraketen, deren Unterstufen wieder landen können, und vollständig wiederverwendbare Raumfähren, die wie ein Flugzeug landend zum Erdboden zurückkehren können.
Weitere Möglichkeiten
Es ist auch möglich, zunächst von der Erde mit einem suborbitalen Raketenflug in den Weltraum zu starten und dann dort mit einem abgekoppelten Raumfahrzeug in einen orbitalen Flug zu beschleunigen. Ein Beispiel dafür war 2019 der Boeing Orbital Flight Test Boe-OFT mit einer Trägerrakete vom Typ Atlas V und einem Raumschiff vom Typ CST-100 Starliner. Das sowjetische Buran-Programm sah auch dieses Prinzip mit der Energija-Trägerrakete vor, es kam aber nur zu einem einzigen unbemannten Einsatz 1988 mit der Raumfähre Buran 1.01, danach wurde das Programm eingestellt.
Low Earth Orbit
Bei einer niedrigen Erdumlaufbahn in einer Höhe von etwa 200 bis 2000 km spricht man von einem Low Earth Orbit (LEO). In diesem Bereich des erdnahen Weltraums ist die Bremswirkung der dünnen Erdatmosphäre noch spürbar. In einem niedrigen LEO kann ein Raumflugkörper nicht für längere Zeiträume ohne eigenen Antrieb verbleiben, da seine Umlaufbahn durch die Reibung mit der Zeit immer niedriger wird. Zum Beispiel bleiben Satelliten bei einer (Apogäums-)höhe von 200 km nur wenige Tage auf der Umlaufbahn. Ab einer Höhe von etwa 800 km verbleiben sie mehr als 10 Jahre im Weltraum, hochfliegende Satelliten praktisch für immer.
Im LEO bewegen sich Raumflugkörper mit einer Geschwindigkeit von etwa 7 km/s und benötigen für einen Umlauf um die Erde etwa 90 bis 100 Minuten. Beispielsweise umkreist die Internationale Raumstation (ISS) die Erde in einer annähernd kreisförmigen niedrigen Erdumlaufbahn, deren Höhe durch die Reibung und durch Bahnanhebungen immer wieder verändert wird und etwa zwischen 320 und 410 km schwankt. Die Versorgungsflüge von der Erde zur ISS, gegebenenfalls auch mit Rücktransport, sind damit klassische Fälle von niedrigen Erdorbitalflügen. Im Durchschnitt finden pro Jahr etwa vier Flüge zur ISS statt.
Perigäumsdrehung
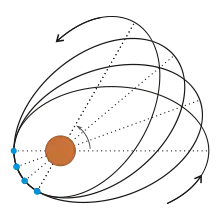
Dadurch, dass die Erde keine perfekte Kugel, sondern abgeplattet ist (siehe Erdfigur), erfahren Erdsatelliten eine Drehung ihrer Apsidenlinie. Dies wird auch als Perigäumsdrehung bezeichnet. Auch die Reibung an der dünnen Erdatmosphäre kann die Perigäumsdrehung beeinflussen. Zudem gibt es auch einen – allerdings äußerst geringen – relativistischen Anteil an der Perigäumsdrehung.
Je nach der Neigung der Orbitalebene kann die Perigäumsdrehung in der Bewegungsrichtung des Satelliten oder rückläufig dazu sein.
Rückkehr von einem Erdorbitalflug
Für eine sichere Rückkehr eines Raumflugkörpers aus einer Umlaufbahn um die Erde ist der Wiedereintritt in die Erdatmosphäre kritisch. Dabei wird der Körper durch die Atmosphäre stark abgebremst und große Kräfte und Hitze wirken auf ihn ein. Objekte ohne Hitzeschild wie etwa Satelliten werden dabei zerstört und verglühen vollständig oder großteils. Größere Fragmente von zerstörten Raumflugkörpern können den Wiedereintritt überstehen und die Erdoberfläche erreichen.
Das meistverwendete unbemannte Versorgungsraumschiff für die ISS, Progress, hat keine Rückkehrkapsel. Es wird für seine Rückkehr zur Erde mit Müll aus der ISS beladen und verglüht beim Wiedereintritt in der Erdatmosphäre. Die Rückkehr von Besatzungsmitgliedern der ISS erfolgt unter anderem mit Raumschiffen vom Typ Sojus.
Geschichte der Erdorbitalflüge
Im Jahr 1942 durchstieß die deutsche militärische Rakete Aggregat 4 erstmals die Grenze zum Weltraum. Der erste Orbitalflug wurde der nächste wichtige Meilenstein der Raumfahrt. Mit ihm als Ziel begann der Wettlauf ins All, und ihn erreichte als erstes die Sowjetunion im Jahr 1957 mit dem Satelliten Sputnik 1. Dieser umkreiste die Erde in 92 Tagen rund 1400 Mal. Mit der Mission Sputnik 5 eines Wostok-Raumschiffs, das zwei Hunde und weitere Tiere an Bord hatte, gelang der Sowjetunion 1960 auch der erste sichere Wiedereintritt nach einem Orbitalflug.
Der erste bemannte Orbitalflug war der Flug von Juri Gagarin mit Wostok 1 im Jahr 1961. Als erste Frau führte Walentina Tereschkowa mit Wostok 6 im Jahr 1963 einen Orbitalflug aus.
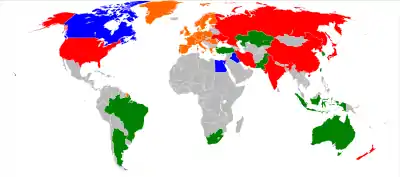
Bald nach diesen sowjetischen Pionierleistungen holte die US-amerikanische Raumfahrt (NASA) auf. Später kamen weitere Weltraumorganisationen und Länder dazu, wie die ESA, die Volksrepublik China und Indien. Stand 2010 wurden in 50 Jahren Raumfahrt mit etwa 4700 Raketenstarts mehr als 6100 Satelliten in den Weltraum gebracht. Stand April 2021 umkreisen knapp 4100 Satelliten die Erde.[8] Von diesen Flügen stammt ein beträchtlicher Weltraummüll, der sich in Umlaufbahnen um die Erde befindet und eine Gefahr für die weitere Raumfahrt darstellt.
Seit 2015 gelang es dem US-amerikanischen Raumfahrtunternehmen SpaceX, die Kosten von Erdorbitalflügen durch Wiederverwendung von Raketenstufen signifikant zu reduzieren.[9]
Touristische Erdorbitalflüge
Der bisherige Weltraumtourismus (eine niedrige zweistellige Anzahl Flüge) umfasst suborbitale Flüge und Erdorbitalflüge. Von den Erdorbitalflügen hatten die bisher meisten ein Andocken an der ISS als Ziel.
Orbitalflüge um die Sonne
Hierunter fallen Raumflugkörper, die nur die Sonne umkreisen, aber keinen anderen Himmelskörper. Sonnenorbiter haben sogenannte heliozentrische Umlaufbahnen, ähnlich wie Asteroiden. Der sonnennächste Punkt der Bahn wird Perihel, der sonnenfernste Punkt Aphel genannt.
Sobald ein Raumflugkörper die Hill-Sphäre der Erde verlässt, wird er im Regelfall zu einem Sonnenorbiter. Erst wenn er die notwendige Fluchtgeschwindigkeit zum Verlassen des Sonnensystems hat – die bei einem Start von der Erde auch die „dritte kosmische Geschwindigkeit“ genannt wird –, oder wenn er (mit beliebiger Geschwindigkeit) die Hill-Sphäre der Sonne verlässt, kann er diesem entkommen.
1959 wurde die sowjetische Mondsonde Luna 1 ungewollt das erste künstliche Objekt in einer heliozentrischen Umlaufbahn.[10] Sie sollte eigentlich auf dem Mond aufschlagen. Sie verfehlte aber ihr Ziel und gelangte so in eine Umlaufbahn um die Sonne zwischen den Bahnen von Erde und Mars. Im gleichen Jahr 1959 flog auch die US-amerikanische Mondsonde Pioneer 4 (gewollt) am Mond vorbei in eine heliozentrische Umlaufbahn.
Koorbitale Flüge
Ein Sonderfall unter den Sonnenorbitern sind Raumflugkörper, die als koorbitales Objekt mit dem System Sonne–Erde in einer 1:1-Bahnresonanz mitrotieren.
Lagrange-Punkte
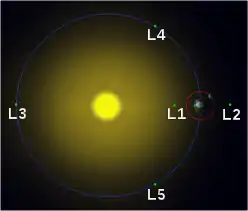
An den Lagrange-Punkten der Erde kann ein Flugkörper mit gelegentlichen Bahnkorrekturen, aber ansonsten ohne Antrieb, die Erde auf ihrer jährlichen Bahn um die Sonne in einem festen Abstand begleiten. Der Flugkörper steht dabei in der Praxis nicht an dem exakten Lagrange-Punkt still, sondern umkreist diesen auf einer speziellen Umlaufbahn. Solche Umlaufbahnen um Lagrange-Punkte sind von ganz anderer Art als keplersche Umlaufbahnen. Es gibt hier verschiedene Fälle, unter anderem Halo-Orbits, Lissajous-Orbits und Lyapunov-Orbits.
Beispiele für Weltraumteleskope, die am sonnenabgewandten Lagrange-Punkt L2 der Erde eingesetzt wurden, sind die WMAP-Raumsonde (2001–2010), das Herschel-Weltraumteleskop (2009–2013), das Planck-Weltraumteleskop (2009–2013), Gaia (seit 2014), Spektr-RG mit dem Hauptinstrument eROSITA (seit 2019) und zukünftig das James Webb Space Telescope.
Nach dem Ende ihrer Mission werden solche Flugkörper typischerweise aus dem Lagrange-Punkt entfernt und in einen Friedhofsorbit um die Sonne gebracht.
Weitere Möglichkeiten für koorbitale Flugbahnen
Weitere Möglichkeiten für koorbitale Flugbahnen sind Hufeisenumlaufbahnen und Quasisatellitenbahnen. Bisher wurden noch keine Raumflugkörper auf eine solche Bahn gebracht, aber es ist prinzipiell denkbar. Des Weiteren gibt es nicht nur bei der Erde, sondern auch bei allen anderen Himmelskörpern die Möglichkeit koorbitaler Flüge.
Orbitalflüge um andere Himmelskörper
Bei der Annäherung an einen Himmelskörper – etwa einen Planeten, Mond oder Kleinkörper – ist die ankommende Bahn eines Flugkörpers eine Hyperbel, da die Annäherung quasi aus dem Unendlichen erfolgt. Um in eine Umlaufbahn um den Himmelskörper einzuschwenken (englisch: orbit insertion), muss ein Raumflugkörper abbremsen und damit Energie abgeben, ansonsten würde er den Himmelskörper auf der hyperbolischen Bahn wieder verlassen. Bei der orbit insertion wird die Relativgeschwindigkeit des Flugkörpers am aktuellen Bahnpunkt unter die Fluchtgeschwindigkeit gebracht. Das geschieht typischerweise mit einem retrograden Triebwerkstoß am Punkt der größten Annäherung. Man kann auch treibstoffsparend ein Swing-by-Manöver zum Abbremsen einsetzen oder die Atmosphäre des Himmelskörpers für eine Atmosphärenbremsung benutzen. Das Orbit-insertion-Manöver ändert die Flugbahn in eine Ellipse und der Flugkörper wird dadurch zu einem Orbiter. Anschließend kann die Umlaufbahn bei Bedarf durch Manöver weiter verändert werden.
Als Orbiter konzipierte Raumsonden und Raumschiffe werden entweder für sich allein eingesetzt oder mit einem Lander kombiniert, der den Orbiter verlässt, um eine harte oder weiche Landung auf dem Himmelskörper auszuführen. Der Orbiter selbst kann am Ende seiner Mission zur Erde zurückfliegen, wie bei den NASA-Mondmissionen Apollo 8 bis Apollo 17 geschehen. Er kann auch sich selbst überlassen werden, bis er irgendwann durch Reibung oder bahnstörende Effekte auf den Himmelskörper abstürzt, oder er kann zu einem gezielten Absturz gebracht werden.
Die folgenden Abschnitte sind chronologisch nach der ersten erfolgreichen Umkreisung des jeweiligen Himmelskörpers sortiert.
Orbitalflüge um den Mond
Raumflugkörper, die Orbitalflüge um den Mond ausführen, werden Mondsatelliten oder Mondorbiter genannt. Der mondnächste bzw. der mondfernste Punkt der Bahn wird Periselen und Aposelen genannt. Niedrige Mondumlaufbahnen (Low lunar orbit oder LLO bezeichnet) unter 100 Kilometern Höhe haben eine Umlaufzeit von etwa zwei Stunden.[11]

Der erste Orbitalflug um den Mond gelang 1966 mit der sowjetischen Mondsonde Luna 10.[12] Die Sonde umkreiste den Mond mindestens 56 Tage lang. Danach brach die Kommunikation zu ihr ab, sodass unbekannt ist, wann und wo sie auf dem Mond einschlug.[13] Auf dem Mond gibt es zwar keine Atmosphärenreibung, aber es gibt Unregelmäßigkeiten im Gravitationsfeld (Mascons), die niedrige Satellitenorbits ohne Bahnkorrekturen stören, was zum Absturz des Satelliten führen kann.[11] Im gleichen Jahr 1966 gelang auch den USA mit Lunar Orbiter 1 eine erste Mondumkreisung. Lunar Orbiter 1 wurde 77 Tage nach dem Erreichen seiner Umlaufbahn zu einem kontrollierten Absturz auf dem Mond gebracht.
Zwischen den Jahren 1968 und 1972 gab es neun bemannte Orbitalflüge um den Mond aus dem Apollo-Programm der USA.
Die Anzahl von Mondsatelliten ist verglichen mit der Anzahl Erdsatelliten verschwindend gering.
Erdorbitalflüge an Lagrange-Punkten des Mondes
Raumflugkörper können auch an Lagrange-Punkten des Systems Erde–Mond stationiert werden. Sie umkreisen dann nicht den Mond, sondern synchron mit dem Mond die Erde.
Bisher führten dies zwei chinesische Raumflugkörper aus, die Sonde Chang’e 5-T1 (2014) und der Relaissatellit Elsternbrücke (seit 2018).
Orbitalflüge um den Mars
Der marsnächste bzw. der marsfernste Punkt einer Umlaufbahn wird Periares und Apares genannt. Bisher wurden insgesamt 18 Orbiter erfolgreich in eine Umlaufbahn um den Mars gebracht, von denen 8 noch in Betrieb sind. Zu den 10 anderen besteht kein Kontakt mehr, sie sind aber vermutlich noch immer im Marsorbit. Wann sie voraussichtlich abstürzen werden, lässt sich nur ungenau voraussagen.
1971 wurde die NASA-Marssonde Mariner 9 die erste Sonde, die in eine Umlaufbahn um einen anderen Planeten einschwenkte.[14] Wenige Wochen später erreichten auch die ersten sowjetischen Sonden Mars 2 und Mars 3 eine Umlaufbahn um den roten Planeten. Mariner 9 war ein Orbiter ohne Lander. Der Lander von Mars 2 stürzte ab. Dem Lander von Mars 3 gelang 1971 als erstem Raumflugkörper eine weiche Landung auf einem anderen Planeten, wenngleich er nur wenige Sekunden nach der Landung außer Funktion ging.
Orbitalflüge um die Venus
Bisher gab es 8 Missionen zur Venus mit einem Venusorbiter. Die erste davon war im Jahr 1975 die sowjetische Sonde Venera 9. Ihr Lander übermittelte das erste Bild von der Oberfläche eines fremden Planeten.[15]

Orbitalflüge um den Jupiter
Der jupiternächste bzw. der jupiterfernste Punkt einer Umlaufbahn wird Perijovum und Apojovum genannt. Zwei Sonden der NASA führten bisher eine Umlaufbahn um den Jupiter aus.
Die 1989 gestartete Sonde Galileo erreichte nach einem Swing-by-Manöver an der Venus (1990) und zwei Swing-by-Manövern an der Erde (1990, 1992), bei denen sie Geschwindigkeit aufnahm, im Jahr 1995 den Gasplaneten. Sie schwenkte dort in eine Umlaufbahn ein und umkreiste den größten Planeten des Sonnensystems, bis sie 2003 beim Ende der Mission gezielt zum Absturz in der Jupiteratmosphäre gebracht wurde.
Die Sonde Juno startete 2011. Sie führte nur ein einziges Swing-by-Manöver an der Erde aus (2013) und trat 2016 in einen Jupiterorbit ein. Eine Besonderheit ihrer Umlaufbahn ist, dass sie polar und stark elliptisch ist. Das ermöglicht die Beobachtung der Polregionen und vermeidet zugleich die starken Strahlungsgürtel des Planeten. Juno befindet sich noch immer im Orbit um den Jupiter (Stand 2021).
Orbitalflüge um Kleinkörper
Der erste Asteroiden-Orbiter, die Sonde NEAR Shoemaker, schwenkte im Jahr 2000 in eine Umlaufbahn um den Asteroiden Eros ein. Nach einem Jahr im Orbit um Eros landete die Sonde erfolgreich auf der Oberfläche des Asteroiden.
Die Sonde Dawn umkreiste 2011 bis 2012 den Asteroiden Vesta. Anschließend verließ sie diesen und flog auf einer Transferbahn weiter zum Zwergplaneten Ceres, den sie seit dem Jahr 2015 umkreist. Seit 2018 ist die Sonde inaktiv, umkreist Ceres aber weiter.
Die Sonde Rosetta umkreiste von 2014 bis 2016 den Kometen Tschurjumow-Gerassimenko. Ihre Mission endete mit einem gezielten Aufprall auf dem Kometen.
Orbitalflug um den Saturn
Eine einzige Sonde, Cassini-Huygens, erreichte bisher eine Umlaufbahn um den Saturn. Sie startete im Jahr 1997 und führte mehrere Swing-by-Manöver aus (Venus 1998 und 1999, Erde 1999, Jupiter 2000). Im Jahr 2004 erreichte sie den Saturn und schwenkte in einen Orbit um ihn ein. Die Landesonde Huygens trennte sich 2005 vom Orbiter Cassini, um auf dem Saturnmond Titan zu landen. Cassini führte die Umkreisung des Saturn fort, bis sie 2017 am Ende ihrer Mission zum Verglühen in der Saturnatmosphäre gebracht wurde.
Orbitalflug um den Merkur
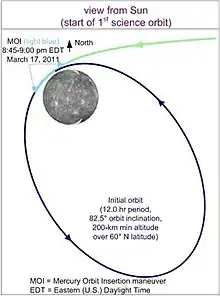
Wegen dessen Nähe zur Sonne ist es technisch schwierig, Merkur anzufliegen, und noch schwieriger, in eine Umlaufbahn um ihn einzuschwenken. Um Merkur von der Erde aus zu erreichen, müsste ein Raumflugkörper nach dem Verlassen des Einflussbereichs der Erde theoretisch zunächst stark abbremsen. Bei der Annäherung an die Sonne würde der Flugkörper jedoch so stark beschleunigen, dass er am Merkur zu schnell wäre, um in einen Orbit um den innersten Planeten einzuschwenken.
Das Ziel gelang bisher nur der NASA-Sonde MESSENGER. Sie wurde 2004 gestartet. Nach zwei Swing-by-Manövern an der Venus (2006, 2007) und drei Swing-by-Manövern am Merkur (2008, 2008, 2009), bei denen die Sonde schrittweise abgebremst wurde, schwenkte sie im Jahr 2011 in eine Umlaufbahn um den Merkur ein. Nach mehreren Einsatzjahren im Merkurorbit wurde die Sonde 2015 mit dem letzten verfügbaren Treibstoff zum gezielten Absturz gebracht.
Weitere Himmelskörper
Zu den Planeten Uranus und Neptun sind bisher nur Vorbeiflugsonden geflogen. Es gibt erste Konzepte für Uranus- und Neptun-Orbiter.
Sämtliche Monde des Sonnensystems außer dem Erdmond, darunter die Jupiter- und Saturnmonde, sind bisher noch nicht umkreist worden.
Siehe auch
Einzelnachweise
- Adam Mann: What’s the difference between orbital and suborbital spaceflight? In: space.com. 10. Februar 2020, abgerufen am 21. September 2021 (englisch).
- Taissija I. Trofimowa: Physik. Springer-Verlag, 2013, ISBN 978-3-322-87254-8, S. 37 (books.google.com).
- Bogdan Povh, Elisabeth Soergel: Anschauliche Physik für Naturwissenschaftler. Springer-Verlag, 2014, ISBN 978-3-642-54496-5, S. 60 (books.google.com).
- Ernst Messerschmid, Stefanos Fasoulas: Raumfahrtsysteme. Eine Einführung mit Übungen und Lösungen. Springer-Verlag, 2010, ISBN 978-3-642-12817-2, S. 86 ff. (books.google.com).
- Rafael Moro-Aguilar: The New Commercial Suborbital Vehicles: An Opportunity for Scientific and Microgravity Research. In: researchgate.net. Microgravity Science and Technology, November 2014, abgerufen am 22. September 2021 (englisch).
- Beate Varnhorn: Bertelsmann. Das neue Universallexikon. wissenmedia Verlag, 2006, ISBN 978-3-577-10298-8, S. 697 (books.google.com).
- Extremer Leichtbau für die Raumfahrt. In: k-zeitung.de. 2019, abgerufen am 22. September 2021.
- Satelliten im Weltraum nach Ländern 2021. In: statista.com. Abgerufen am 21. September 2021.
- Michael Belfiore: The Rocketeer. In: foreignpolicy.com. Abgerufen am 21. September 2021 (amerikanisches Englisch).
- Asif A. Siddiqi: Beyond Earth. A Chronicle of Deep Space Exploration, 1958–2016 (= The NASA history series), second. Auflage, NASA History Program Office, Washington, D.C. 2018, ISBN 978-1-62683-042-4, SP2018-4041.
- Bizarre Lunar Orbits. In: science.nasa.gov. NASA, 6. November 2006, abgerufen am 9. Dezember 2012: „Lunar mascons make most low lunar orbits unstable … As a satellite passes 50 or 60 miles overhead, the mascons pull it forward, back, left, right, or down, the exact direction and magnitude of the tugging depends on the satellite’s trajectory. Absent any periodic boosts from onboard rockets to correct the orbit, most satellites released into low lunar orbits (under about 60 miles or 100 km) will eventually crash into the Moon. … [There are] a number of ‘frozen orbits’ where a spacecraft can stay in a low lunar orbit indefinitely. They occur at four inclinations: 27°, 50°, 76°, and 86° – the last one being nearly over the lunar poles. The orbit of the relatively long-lived Apollo 15 subsatellite PFS-1 had an inclination of 28°, which turned out to be close to the inclination of one of the frozen orbits – but poor PFS-2 was cursed with an inclination of only 11°.“
- Asif A. Siddiqi: Beyond Earth. A Chronicle of Deep Space Exploration, 1958–2016 (= The NASA history series), second. Auflage, NASA History Program Office, Washington, D.C. 2018, ISBN 9781626830424, S. 1, SP2018-4041.
- NASA – NSSDCA – Spacecraft – Details. In: nssdc.gsfc.nasa.gov. NASA, abgerufen am 1. Oktober 2021.
- Mariner 9: Details. National Space Science Data Center. Abgerufen am 28. Dezember 2011.
- Solar System Exploration Multimedia Gallery: Venera 9. In: NASA. Archiviert vom Original am 3. August 2009. Abgerufen am 7. August 2009.