Geostationärer Satellit

Ein geostationärer Satellit ist ein künstlicher Erdsatellit, der sich auf einer Kreisbahn 35.786 km über der Erdoberfläche über dem Äquator befindet. Dort befindet sich die geostationäre Umlaufbahn (engl.: Geostationary Earth Orbit, kurz GEO), d. h. dort stationierte Satelliten bewegen sich mit einer Winkelgeschwindigkeit von einer Erdumrundung pro Tag und folgen der Erdrotation mit einer Eigengeschwindigkeit von etwa 3,07 km/s. Dadurch befinden sich geostationäre Satelliten im Idealfall immer über demselben Punkt der Erdoberfläche bzw. des Äquators.

GOES I – ein geostationärer Wettersatellit

Wie Nachrichtensatelliten im GEO stehen (Die Solarzellpaddel zeigen immer in Nord-Süd-Richtung)

Die geostationäre Bahn im Verhältnis zum Abstand Erde-Mond

Bei einer Langzeitbelichtung erscheinen geostationäre Satelliten als Punkte, während die Sterne scheinbar wandern: Hier sind zwei kommerzielle Satelliten zu sehen, und ein geheimer, militärischer Satellit (USA 207, 2009-047A)

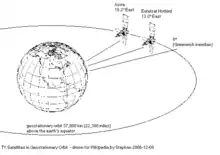
Typische Beispiele für geostationäre Satelliten sind Kommunikationssatelliten, Fernsehsatelliten und Wettersatelliten.

Ein von der Erde aus gesendetes Radiosignal, das ein geostationärer Satellit zurück an einen Empfänger auf der Erde weiterleitet, erfährt aufgrund der vom Breitengrad abhängigen Entfernung von ca. 35.800 bis 41.700 Kilometern, welche zweimal zu durchlaufen ist, und der Lichtgeschwindigkeit, die auch für Radiowellen gilt, eine Verzögerung (Latenzzeit) von ungefähr 0,24 bis 0,28 Sekunden. Bei digitaler Übertragung vergrößert der Einsatz von Datenkompression, Verschlüsselung oder Datenkodierung die Verzögerungszeiten zusätzlich.

Bauarten

Es gibt zwei unterschiedliche Bauarten geostationärer Satelliten.

Spinstabilisierte Satelliten

Ein spinstabilisierter INTELSAT IVA im Bau

Spinstabilisierte Satelliten wurden zuerst entwickelt. Sie sind trommelförmig, und ihre Mantelfläche ist mit Solarzellen bedeckt. Die Spinachse steht parallel zum Rotationsvektor der Satellitenbahn und damit stets senkrecht auf dem momentanen Bahngeschwindigkeitsvektor und wegen der äquatoriellen Bahn auch in Nord-Süd-Richtung, also parallel zur Erdachse.

Wenn der Satellit nicht gerade den Erdschatten durchkreuzt, so werden durch den Spin die längs des Umfangs nebeneinander angeordneten Solarzellen zeitlich nacheinander zur Sonne hin ausgerichtet, wobei zu jedem Zeitpunkt eine Hälfte der Zellen ganz abgeschattet und die andere Hälfte in mehr oder weniger günstigen Winkeln beschienen ist. Nachrichtensatelliten dieses Typs haben in der Regel auf ihrer (nördlichen) Oberseite ein entdralltes Antennenmodul mit fest auf bestimmte Gebiete der Erde ausgerichteten Richtantenne(n). Die Schubdüse des Apogäumsmotors ragt aus der (südlichen) Unterseite des Satelliten.

Drall- oder dreiachsenstabilisierte Satelliten

UFO-Satellit mit einem Hauptkörper fester Ausrichtung

Drall- oder dreiachsenstabilisierte Satelliten haben in der Regel einen quaderförmigen Hauptkörper. Die Vorderseite des Hauptkörpers ist zur Erde ausgerichtet. Die Rückseite dagegen zeigt zum Zenit, und aus ihr ragt der Apogäumsmotor hinaus. Die nach Norden und Süden zeigenden Seiten tragen die Solarzellenflügel, die der Sonne nachgeführt werden, während der Satellit um die Erde kreist.

Die Vorderseite trägt die zur Erde ausgerichteten Instrumente – oder bei einigen Nachrichtensatelliten ein Antennenmodul mit (manchmal ausklappbaren) Richtantenne(n). Diese umgeben den Fuß eines Turmes, der die Hornstrahler trägt, die in den Brennpunkten der Richtantenne(n) stehen. Bei anderen Nachrichtensatelliten sind die Hornstrahler an der oberen Außenkante des Hauptkörpers angebracht und bestrahlen sehr große Richtantennen, die zu groß sind, um auf der Oberseite angebracht zu werden. Sie sind auf den noch freien nach Osten und Westen ausgerichteten Seiten angebracht und werden nach dem Start ausgeklappt. Es gibt auch Satelliten, die sowohl Antennen auf der Oberseite wie auf den westlichen und östlichen Seiten haben.

Einschuss

Typischerweise bringt die Trägerrakete den Satelliten auf eine stark elliptische geostationäre Transferbahn (GTO). Von dort befördert ihn der satelliteneigene Apogäumsmotor in die geostationäre Umlaufbahn (GEO), meist mit einem elektrischen Antrieb.[1] Dabei verbraucht der Satellit den größten Teil seines Treibstoff- beziehungsweise Stützmassenvorrates (meistens Xenon, bei chemischen Antrieben Stickstofftetroxid und Monomethylhydrazin), sodass er nach der Ankunft im GEO nur noch etwa halb so viel Masse besitzt wie beim Start. Die restlichen Treibstoffreserven reichen dann aus, um alle Bahnkorrekturen während der Lebensdauer des Satelliten im GEO vorzunehmen.

Dass die Trägerrakete den Satelliten direkt im GEO absetzt, kommt nur bei russischen Satelliten und US-amerikanischen Militärsatelliten vor. Es wird erwogen, eine neue wiederzündbare Ariane-5-Oberstufe einzuführen, die ebenfalls Satelliten direkt in den GEO bringen könnte.

Die Kosten für den Transport von Nutzlasten in den GTO liegen bei 30.000 bis 50.000 Euro/kg, für den in den GEO bei 300.000 bis 400.000 Euro/kg

Satellitenbahn

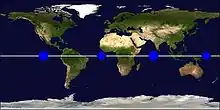
Stabile (●) und labile (◆) Satellitenpositionen

Der Einfluss des Mondes, der Sonne und insbesondere der Erddeformationen stört die geostationäre Umlaufbahn. Nur auf vier Positionen hält ein Satellit seinen Standort, und nur zwei von ihnen sind stabil: 105,3° W und 75,1° O.[2][3][4] Die anderen beiden, 11,5° W und 161,9° O, sind labil.[2][3][4][5] Kleine Störgrößen bewirken einen Drift zu den stabilen Lagen. Die Positionierung eines Satelliten außerhalb dieser Punkte erfordert daher fortlaufend Bahnkorrekturen. Satelliten, die außer Kontrolle geraten und nicht mehr auf einen Friedhofsorbit transferiert werden können, sammeln sich an diesen beiden Punkten. Zurzeit (2010) sollen es mehr als 160 sein.[2]

Die Bahnstörungen beeinflussen auch die Bahnneigung. Ohne Korrekturen vergrößert sie sich je nach Position um etwa 0,5° pro Jahr. Der Satellit steht nicht mehr ortsfest am Himmel, sondern bewegt sich relativ zur Erde auf einer Kurve in Form einer Acht. Die Abweichung von der Kreisform hin zu einer elliptischen Bahn drückt sich in einer Asymmetrie der Kurve aus, ähnlich wie die der Analemma-Kurve der Sonne. Bahnkorrekturen in Nord-Süd-Richtung erfordern sehr viel mehr Treibstoff als Verschiebungen entlang des Äquators. Deshalb lassen die Betreiber alte Satelliten mit fast erschöpften Treibstoffvorräten, wenn möglich, im sogenannten Inclined-Orbit pendeln. Bei einer N/S-Schwankung um 10° beträgt die W/O Variation etwa 0,5°.

Die Internationale Fernmeldeunion teilt Frequenzen und Satellitenpositionen zu, damit Satelliten sich nicht gegenseitig stören. Früher betrug der Abstand 4° zum Nachbarsatelliten, der auf der gleichen Frequenz strahlte. Wegen der großen Nachfrage nach Satellitenpositionen wurden die Abstände auf 2°, entsprechend 1400 Kilometer, reduziert. Die eigentliche zugeteilte Satellitenposition ist eine Box, in der die Betreiber ihre Satelliten auf ± 0,14° positionieren müssen, gleichbedeutend mit einer Ost-West-Drift von weniger als 100 Kilometern. Die Radialdrift darf nicht mehr als um 75 Kilometer variieren.

Co-Positionierung

Es ist möglich, auf einer Satellitenposition mehr als einen Satelliten zu positionieren. In diesem Fall befinden sich sämtliche Co-positionierte Satelliten innerhalb der zugewiesenen Box. Auf einer Satellitenposition ist es heutzutage möglich, acht Satelliten zu positionieren.[6]

Energieversorgung bei Eklipse, Sun outage

Ein geostationärer Satellit bezieht seine Energie nahezu ganzjährig vollständig aus Solarzellen. Die Knoten der geostationären Umlaufbahn liegen zu Frühlings- und Herbstbeginn in der Nähe der Verbindungslinie Sonne-Erde und damit im Erdschatten. Deshalb steht er von März bis Mitte April und September bis Mitte Oktober nachts für maximal 70 Minuten im Erdschatten. Während der Zeit dieser Eklipse beziehen die Satelliten ihre Energie aus Akkumulatoren, die zuvor von den Solarzellen aufgeladen wurden, oder schränken ihre Leistung ein (Beispiel: TV-SAT). Zweimal im Jahr liegen zu einer bestimmten Tageszeit Satellit, Erde und Sonne nahezu auf einer Linie. Dann steht die Sonne von der Antenne aus gesehen an mehreren aufeinanderfolgenden Tagen für wenige Minuten dicht beim Satelliten. Die Mikrowellenstrahlung der Sonne überlagert dann die des Satelliten, und es kommt zu einer kurzzeitigen Verschlechterung bzw. Unterbrechung der Satellitenverbindung (englisch sun outage). Die genaue Eintrittszeit dieses Ereignisses hängt von der Position des betrachteten Satelliten sowie der Empfängerposition auf der Erde ab; weiterhin haben Antennendurchmesser und Übertragungsfrequenz Auswirkungen auf die Dauer der Unterbrechung.

Berechnung der Flughöhe

Die nachfolgende Berechnung geht vom klassischen Newtonschen Gravitationsgesetz aus, vernachlässigt also relativistische Effekte. Des Weiteren wird ein ungestörtes radialsymmetrisches Gravitationsfeld der Erde angenommen, und die Masse des Satelliten soll verschwindend gering im Vergleich zur Masse der Erde sein.

Damit sich der Satellit auf einer Kreisbahn um die Erde bewegt, muss er eine kontinuierliche Beschleunigung zum Zentrum des Kreises, d. h. zum Erdmittelpunkt erfahren. Die diese Beschleunigung auslösende Kraft kommt aus der Gravitationswechselwirkung zwischen Erde und Satellit. Es gilt:

G\;{\frac {m_{s}\;M_{\oplus }}{{r_{s}}^{2}}}=m_{s}\;\omega ^{2}\;r_{s}

Linke Seite: Gewichtskraft aufgrund der Gravitationswechselwirkung zwischen Erdmasse $M_{\oplus }$ und Satellitenmasse $m_{s}$ , rechte Seite: Zentralkraft, die für eine Kreisbahn mit dem Radius $r_{s}$ und der Winkelgeschwindigkeit $\omega$ notwendig ist. Diese Annahme einer Kreisbahn um den Erdmittelpunkt ist in Näherung nur dann gerechtfertigt, wenn die Satellitenmasse als sehr klein gegen die Erdmasse angenommen werden kann, also $m_{s}\ll M_{\oplus }$ .

Man erkennt dann aber, dass die Masse des Satelliten $m_{s}$ herausgekürzt werden kann, der Bahnradius $r_{s}$ also von der Satellitenmasse unabhängig ist. Mit der Beziehung $\omega ={\tfrac {2\pi }{T_{s}}}$ und dem Auflösen der Gleichung nach dem Bahnradius $r_{s}$ erhält man somit:

r_{s}={\sqrt[{3}]{{G\;M_{\oplus }\;{T_{s}}^{2}} \over {4\pi ^{2}}}}

Für die Umlaufzeit $T_{s}$ des Satelliten ist die siderische Tageslänge einzusetzen. Das Produkt $GM_{\oplus }$ ist aus messtechnischen Gründen genauer bekannt als die Einzelterme $G$ (Gravitationskonstante) und $M_{\oplus }$ (Erdmasse). Die genauen Zahlenwerte sind:

GM_{\oplus }=3{,}9860042\cdot 10^{14}\,\mathrm {\frac {m^{3}}{s^{2}}}

T_{s}=8{,}6164099\cdot 10^{4}\,\mathrm {s}

Mit obiger Formel ergibt sich damit ein Bahnradius von rund 42.164 km. Zur Berechnung der Flughöhe muss davon noch der Radius der Erde am Äquator, 6.378 km, abgezogen werden, der wegen der Abplattung der Pole etwas größer ist als der mittlere Erdradius. Damit ergibt sich die Flughöhe über dem Äquator zu 35.786 km.

Sichtbarkeit eines Satelliten von der Erde

Da ein geostationärer Satellit von einem Beobachter auf der Erde aus gesehen stillsteht, bleiben der horizontale und der vertikale Sichtwinkel (Azimut und Elevation) konstant. Sie hängen nur von der geographischen Breite $\phi _{T}$ und Länge $\lambda _{T}$ des Betrachters und der geographischen Länge $\lambda _{S}$ des Satelliten ab. Die geographische Breite des geostationären Satelliten ist immer 0, und seine Entfernung vom Erdmittelpunkt $r_{S}$ beträgt 42 164 km, der Erdradius $r_{E}$ ist 6 378 km. Die Sichtwinkel, die auch für eine Antennenausrichtung verwendet werden können, werden folgendermaßen berechnet:[7]

Unterschied der geographischen Längen

\Delta \lambda =\lambda _{T}-\lambda _{S}

Dabei sind östliche Längen positiv, westliche Längen negativ zu zählen. Liegt

\Delta \lambda

nicht zwischen −180° und +180°, sind 360° zu addieren oder subtrahieren.

Winkel zwischen Antennenstandort und Subsatellitenpunkt

Diese Formel berechnet den Zentriwinkel der Orthodrome zwischen dem Standort des Beobachters und dem Punkt, der auf der Erdoberfläche direkt unter dem Satelliten liegt.

\cos \delta =\cos \phi _{T}\cdot \cos \Delta \lambda

Horizontale Ausrichtung (Azimut)

Der Azimut $\alpha$ wird von Norden über Osten gemessen.

\cos \alpha =-{\frac {\tan \phi _{T}}{\tan \delta }}

Hier sind einige Fallunterscheidungen notwendig:

	$\Delta \lambda <0$ Der Beobachter befindet sich weiter westlich als der Satellit	$\Delta \lambda =0$ Der Beobachter befindet sich auf demselben Längengrad wie der Satellit	$\Delta \lambda >0$ Der Beobachter befindet sich weiter östlich als der Satellit	$\Delta \lambda =180^{\circ }$ Der Beobachter befindet sich auf dem Längengrad gegenüber dem Satellit
$\phi _{T}>0$ (Beobachter auf der Nordhalbkugel)	Der Azimut liegt zwischen 0° und 180°	Der Azimut beträgt 180° (Süd)	Der Azimut liegt zwischen 180° und 360°	Der Azimut beträgt 0° (Nord)
$\phi _{T}=0$ (Beobachter am Äquator)		Der Satellit steht direkt über dem Beobachter im Zenit. Der Azimut ist nicht definiert, die Elevation beträgt 90°.		Der Satellit steht auf der gegenüberliegenden Seite der Erde im Nadir. Der Azimut ist nicht definiert, die Elevation beträgt −90°.
$\phi _{T}<0$ (Beobachter auf der Südhalbkugel)		Der Azimut beträgt 0° (Nord)		Der Azimut beträgt 180° (Süd)

Vertikale Ausrichtung (Elevation)

Die Elevation $\epsilon$ ist der Winkel zwischen Horizont und Satellit. Steht der Satellit unter dem Horizont, ist die Elevation negativ.

\tan \epsilon ={\frac {\cos \delta -{\frac {r_{E}}{r_{S}}}}{\sin \delta }}

Entfernung zum Satelliten

d=r_{S}\cdot {\sqrt {1-2\cdot {\frac {r_{E}}{r_{S}}}\cdot \cos \delta +\left({\frac {r_{E}}{r_{S}}}\right)^{2}}}

Die Entfernung zum Satelliten beträgt mindestens 35 786 km für einen Satelliten im Zenit. Für einen Satelliten am Horizont kann dieser Wert bis auf 41 670 km steigen.

Numerische Vereinfachung

Das Verhältnis $r_{E}/r_{S}$ beträgt 0,151, so dass die Formeln für Elevation und Entfernung auch folgendermaßen geschrieben werden können:

\tan \epsilon ={\frac {\cos \delta -0{,}151}{\sin \delta }}

d=r_{S}\cdot {\sqrt {1-0{,}302\cdot \cos \delta +\left(0{,}151\right)^{2}}}=r_{S}\cdot {\sqrt {1{,}023-0{,}302\cdot \cos \delta }}

Grafik

Geostationärer Satellitenorbit, von 30°, 50° und 70° geographischer Breite aus gesehen.

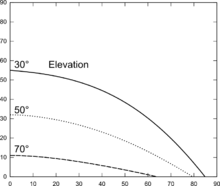
Die Grafik rechts zeigt den geostationären Satellitenorbit für verschiedene Standpunkte auf der Nordhalbkugel der Erde. Oberhalb 81° geographischer Breite ist ein geostationärer Satellit von der Erde aus nicht mehr zu sehen. Bei 70° Breite (gestrichelte Linie) steht er maximal 11° über dem Horizont im Süden. Ungefähr bei Ost-Südost bzw. West-Südwest (63°) schneidet der Orbit den Horizont. Eine Antenne auf 50° Breite (punktierte Linie) kann den Bereich von Süd bis OSO bzw. WSW für den Satellitenempfang nutzen, da der Satellit mit mindestens 10° Elevation ausreichend hoch über dem Horizont steht.

Ausleuchtzone

Größe der Ausleuchtzone einer Parabolantenne auf einem geostationären Satelliten für verschiedene Frequenzbänder.

Die Ausleuchtungszone eines geostationären Satelliten (theoretisch maximal 42 % der Erdoberfläche) hängt von der Richtwirkung seiner Antennen ab. Signale von Antennen mit geringer Richtwirkung sind überall dort zu empfangen, wo auch eine geometrische Sichtbarkeit zum Satelliten besteht. Mit Hochgewinnantennen lässt sich der Empfangsbereich auf ausgewählte Bereiche auf der Erde fokussieren. So möchten europäische Satellitenbetreiber oft, dass ihre Satelliten nur Europa ausleuchten. Das Diagramm gibt beispielsweise Auskunft, dass eine Antenne mit 2 Metern Durchmesser im Ku-Band auf der Erde eine Fläche von 500 Kilometer Durchmesser erfasst. Mit geeigneten Multibeam-Antennen und Beam-Forming Elementen entsteht daraus eine langgestreckte Bestrahlungsfläche, die das europäische Festland von der iberischen Halbinsel bis Polen erfasst.

Eine andere Methode zur Beeinflussung der Form der Ausleuchtzone ist, dass der Satellit elliptische Sendeantennen verwendet, die zur genaueren Formgebung des Sendegebietes schräg auf dem Satelliten angebracht werden können. Diese bündeln das Signal an ihrer breiteren Seite stärker, so dass die Ausleuchtzone auf der Erde in der entsprechenden Richtung schmaler wird.[8]

Beispiele für geostationäre Satelliten

Kommunikationssatelliten

Wettersatelliten

Siehe auch

Liste der geostationären Satelliten

Weblinks

Einzelnachweise

Arianespace reveals manifest, notes launch market variety. In: Spacenews. 9. September 2019, abgerufen am 9. September 2019.
Peter B. de Selding: Out-of-Control Satellite Threatens Other Nearby Spacecraft. space.com, 3. Mai 2010, abgerufen am 4. Mai 2010 (englisch): „Depending on their position at the time of failure, these satellites tend to migrate toward one of two libration points, at 105 degrees west and 75 degrees east. Figures compiled by XL Insurance of New York, an underwriter of space risks, say that more than 160 satellites are gathered at these two points“
E. M. Soop: Handbook of Geostationary Orbits. Springer Science & Business Media, 1994, ISBN 978-0-792-33054-7, S. 71 (eingeschränkte Vorschau in der Google-Buchsuche).
Peter Berlin: The Geostationary Applications Satellite. Cambridge University Press, 1988, ISBN 978-0-521-33525-6, S. 64 (eingeschränkte Vorschau in der Google-Buchsuche).
Wolfgang Steiner, Martin Schagerl: Raumflugmechanik, Springer, Berlin, Heidelberg 2004, ISBN 3-540-20761-9, S. 156 f.
Karl-Otto Saur: Klipp und klar, 100× Fernsehen und Hörfunk. Bibliographisches Institut AG, Mannheim 1978, ISBN 3-411-01711-2, S. 68
H. Paul Shuch: Calculating antenna bearings for geostationary satellites. (PDF) In: Ham Radio 11(5). Mai 1978, S. 67–69, archiviert vom Original am 28. September 2006; abgerufen am 24. Januar 2009 (englisch).
Hans-Martin Fischer: Europäische Nachrichten-Satelliten, Von Intelsat bis TV-Sat. Stedinger, Lemwerder 2006, ISBN 3-927697-44-3, S. 45.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Arianespace reveals manifest, notes launch market variety. In: Spacenews. 9. September 2019, abgerufen am 9. September 2019.

[selding-2] Peter B. de Selding: Out-of-Control Satellite Threatens Other Nearby Spacecraft. space.com, 3. Mai 2010, abgerufen am 4. Mai 2010 (englisch): „Depending on their position at the time of failure, these satellites tend to migrate toward one of two libration points, at 105 degrees west and 75 degrees east. Figures compiled by XL Insurance of New York, an underwriter of space risks, say that more than 160 satellites are gathered at these two points“

[r105752-3] E. M. Soop: Handbook of Geostationary Orbits. Springer Science & Business Media, 1994, ISBN 978-0-792-33054-7, S. 71 (eingeschränkte Vorschau in der Google-Buchsuche).

[r105753-4] Peter Berlin: The Geostationary Applications Satellite. Cambridge University Press, 1988, ISBN 978-0-521-33525-6, S. 64 (eingeschränkte Vorschau in der Google-Buchsuche).

[5] Wolfgang Steiner, Martin Schagerl: Raumflugmechanik, Springer, Berlin, Heidelberg 2004, ISBN 3-540-20761-9, S. 156 f.

[6] Karl-Otto Saur: Klipp und klar, 100× Fernsehen und Hörfunk. Bibliographisches Institut AG, Mannheim 1978, ISBN 3-411-01711-2, S. 68

[7] H. Paul Shuch: Calculating antenna bearings for geostationary satellites. (PDF) In: Ham Radio 11(5). Mai 1978, S. 67–69, archiviert vom Original am 28. September 2006; abgerufen am 24. Januar 2009 (englisch).

[8] Hans-Martin Fischer: Europäische Nachrichten-Satelliten, Von Intelsat bis TV-Sat. Stedinger, Lemwerder 2006, ISBN 3-927697-44-3, S. 45.