Hill-Sphäre
Als Hill-Sphäre, auch Hill-Raum, wird die Umgebung eines Körpers bezeichnet, in der seine Gravitationskraft wirkungsvoller ist als die eines anderen, massereichen Körpers, den er umkreist. Das etwa kugelförmige Gebiet wurde nach dem in der theoretischen Astronomie wirkenden Mathematiker George William Hill benannt. Seine Arbeit beruhte vor allem auf den Schriften von Édouard Roche.
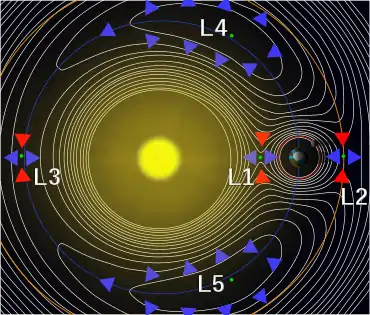
Parameter
Die äußere Grenze der Hill-Sphäre hängt ab von:
- der Gravitationskraft, die durch den Zentralkörper verursacht wird,
- der Gravitationskraft, die durch den umkreisenden Körper verursacht wird und
- der Zentrifugalkraft in einem mit dem umkreisenden Körper mitbewegten Bezugssystem.
Innerhalb der Hill-Sphäre ist die Summe dieser drei Kräfte zu dem umkreisenden Körper hin gerichtet. Dabei entspricht die Grenze der Hill-Sphäre, der Hill-Radius, der Entfernung bis zum ersten bzw. zweiten Lagrange-Punkt:[1]
wobei
- a die Entfernung der Massezentren der beiden Körper,
- m die Masse des umkreisenden Körpers und
- M die Masse des Zentralkörpers ist.
Bahnstabilität
Die Bahn eines kleinen Körpers („Mond“), der sich innerhalb der Hill-Sphäre des um den Zentralkörper („Sonne“) laufenden Objekts („Planet“) befindet, ist im äußeren Bereich der Sphäre äußerst instabil, so dass er die Hill-Sphäre mit hoher Wahrscheinlichkeit in kurzer Zeit verlassen kann. Nur innerhalb einer Stabilitätszone kann die Bahn des „Mondes“ sinnvoll als eine gestörte Ellipsenbahn mit zeitlich veränderlichen Bahnelementen dargestellt werden. Die Größe dieser Zone stabiler Orbits hängt von der Umlaufrichtung des „Mondes“ ab:
- für prograde Bahnen, also solche, die dieselbe Umlaufrichtung haben, in der auch der „Planet“ die „Sonne“ umkreist, erstreckt sie sich bis zu einem Abstand von knapp 50 % des Hill-Radius;
- für retrograde Bahnen liegt die Grenze etwas weiter außen bei knapp 70 % des Hill-Radius.[1]
Beispiele
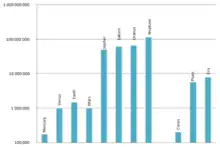
Für die Erde mit einer Masse von m = 5,97·1024 kg im Orbit um die Sonne mit einer Masse M = 1,99·1030 kg in einer Entfernung von a = 1 AE = 149,6·106 km ergibt sich ein Hill-Radius von ungefähr 1,5·106 km = 0,01 AE.
Da der Mond ungefähr 0,37·106 km von der Erde entfernt ist, befindet er sich weit innerhalb der Hill-Sphäre.
Die Hill-Sphäre von Jupiter hat einen mittleren Radius von 0,35 Astronomischen Einheiten. Damit ist sie fast so groß wie die große Bahnhalbachse von Merkur und nimmt von der Erde aus gesehen mehr als das Fünfzehnfache des Vollmonddurchmessers ein. Der äußerste bekannte Jupitermond S/2003 J 2 hat eine große Halbachse, die knapp 60 % des Hill-Radius entspricht, und umläuft den Planeten retrograd. Sein jupiterfernster Bahnpunkt, die Apoapsis, liegt mit 68 % des Hill-Radius allerdings am äußersten Rand der Stabilitätszone. Der äußerste bekannte Mond, der den Planeten prograd umläuft, ist Carpo, dessen Halbachse etwa 32 % des Hill-Radius ausmacht und dessen Apoapsis bei knapp 48 % liegt. Die Bahn dieses Mondes ist allerdings in vielerlei Hinsicht ungewöhnlich und möglicherweise über längere Zeiträume instabil. Die Monde der Himalia-Gruppe, die etwas kleinere Bahnachsen von etwa 22 % des Hill-Radius besitzen, erreichen an den fernsten Bahnpunkten etwa 30 % des Hill-Radius. Die am weitesten entfernten Jupitermonde erreichen sogar bis zu 50 % des Hill-Radius; ihre Bahnen verlaufen dabei nahezu retrograd. Beispiele hier sind etwa die Carme-Gruppe und der Satellit (Mond) S/2003 J 2.
Die Hill-Sphären der Monde sind in aller Regel sehr klein und damit auch die Wahrscheinlichkeit, dass darin Mondtrabanten über lange Zeit auf stabilen Umlaufbahnen kreisen können. Am ehesten ist das bei großen Monden möglich, die sich in großem Abstand zu ihrem Planeten bewegen. Die größte Hill-Sphäre unter den natürlichen Satelliten des Sonnensystems besitzt der Erdmond mit einem Radius von 9,2 Erdradien, gefolgt vom Saturnmond Titan (Hill-Radius 8,2 Erdradien) und Jupitermond Kallisto (7,9 Erdradien).
Weblinks
- Axel M. Quetz: Zum Nachdenken: Die Hill-Sphäre der Erde. In: spektrum.de. 18. Mai 2012, abgerufen am 23. Januar 2016.
Belege
- Scott S. Sheppard, David Jewitt, Jan Kleyna: Ultra Deep Survey for Irregular Satellites of Uranus: Limits to Completeness. In: The Astronomical Journal. 129, 2005, S. 518–523. arxiv:astro-ph/0410059. doi:10.1086/426329.