Apsis (Astronomie)
Apsis oder Apside[1] (Plural Apsiden) bezeichnet in der Astronomie einen der zwei Hauptscheitel der elliptischen Umlaufbahn eines Himmelskörpers um einen anderen als Zentralkörper.
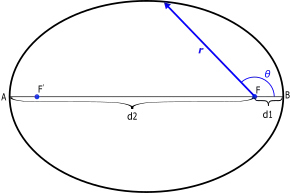
A = Apoapsis (d2 = Apoapsisdistanz)
B = Periapsis (d1 = Periapsisdistanz)
(F, rechts = Gravitationszentrum = einer der beiden Brennpunkte)
Die Apoapsis ist derjenige Scheitel mit der größten Entfernung zum Zentralkörper und die Periapsis der mit der geringsten; beide gemeinsam werden Apsiden genannt, ihre Verbindungsgerade heißt Apsidenlinie.
Bei einer Umlaufbahn – beispielsweise von Planeten – um die Sonne bezeichnet Perihel den sonnennächsten und Aphel den sonnenfernsten Bahnpunkt.
Bei einer Umlaufbahn – beispielsweise des Mondes – um die Erde bezeichnet Perigäum den erdnächsten und Apogäum den erdfernsten Bahnpunkt.
Wortherkunft
Apsis hat als altgriechisches Wort ἁψίς hapsís (im ionischen Dialekt ohne Hauchlaut ἀψίς apsís) die Bedeutungen „Verknüpfung“, „Maschen des Garnes“, am häufigsten jedoch „Gewölbe“, speziell „Triumphbogen“ oder „Himmelsgewölbe“.[2] Mit der Bedeutung „Gewölbe“ wurde es für die in der Architektur gebräuchliche Bezeichnung Apsis entlehnt. In der Astronomie wird es nicht nur im Sinne von „(Himmels-) Gewölbe“, sondern auch für den Scheitel einer Bahnkurve verwendet. Apo- und peri- sind Vorsilben mit der Bedeutung „von einem Orte weg“, „entfernt“[3] bzw. „um etwas herum“, „in der Nähe“.[4]
Abgeleitete Begriffe
Bezogen auf Zentralkörper
| Sonne: Perihel und Aphel | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Apsiden elliptischer Umlaufbahnen um bestimmte Zentralkörper werden oft besonders benannt. Für die auf Sonne, Erde oder Mond bezogenen gibt es häufig verwendete Fachausdrücke, gebildet aus einem vom griechischen Namen abgeleiteten Teil und den Vorsilben Ap(o)- für den fernen bzw. Peri- für den nahen Hauptscheitelpunkt.
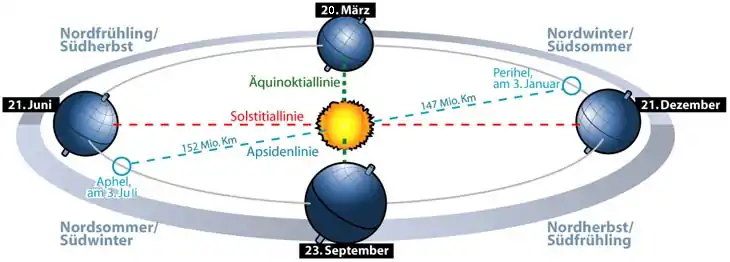
- -hel zu helios „Sonne“: Das Perihel ist der sonnennächste, das Aphel der sonnenfernste Punkt einer Umlaufbahn um die Sonne. Die Erde ist um den 3. Januar der Sonne am nächsten (ca. 147,1 Mio. km bzw. 0,983 AE) und um den 5. Juli am entferntesten (ca. 152,1 Mio. km bzw. 1,017 AE). Die Differenz von etwa 5 Mio. km entspricht einer Exzentrizität der Erdbahn von etwa 0,017.
- -gäum zu gaia „Erde“; siehe auch Erdnähe: Perigäum und Apogäum sind der erdnächste bzw. der erdfernste Punkt.
- Beim Mond unterscheiden sich durch die merklich elliptische Form seiner Bahn (Exzentrizität 0,055) die beiden Entfernungen 406.740 km und 356.410 km um über 13 Prozent (bezogen auf die große Halbachse der Ellipse von 384.405 km Länge).
- Künstliche Erdsatelliten: Die Apsiden künstlicher Erdsatelliten werden ebenso genannt wie die des Erdmondes.
- Angegeben als Höhe über der Erdoberfläche, fällt ihr Unterschied deutlicher auf als bei Angabe geozentrischer Distanzen. Würde beispielsweise eine etwa 500 km hoch über der Erdoberfläche (6.371 km vom Erdmittelpunkt entfernt)– liegende kreisförmige Umlaufbahn auf eine Exzentrizität von 0,055 geändert, variierte die Höhe etwa zwischen 122 km und 878 km. Satellitenbahnen mit Perigäen unter 200 km über Erdoberfläche sind aber wegen der hohen Bremswirkung der Atmosphäre wenig stabil. Hochexzentrische Umlaufbahnen werden deshalb sehr hoch angelegt, wie z. B. die Tundra-Orbits mit Apogäen über 40.000 km.
- -selen zu selene „Mond“: Periselen und Aposelen sind der mondnächste bzw. der mondfernste Punkt der Bahn eines den Mond umkreisenden Körpers (englisch auch Perilune bzw. Apolune). Zum Beispiel hatte der dritte Lunar Orbiter (1967) zunächst ein Periselen von 210 km Höhe und ein Aposelen von 1790 km. Nach vier Tagen wurde die Bahn auf 45 km und 1850 km umgewandelt, um mehr hochauflösende Fotos zu gewinnen.
- -astron zu griechisch astron „Stern“: Periastron und Apoastron: Der Punkt auf der Umlaufbahn eines Doppelstern-Partners, auf dem dieser am nächsten bzw. am weitesten von seinem Begleiter entfernt ist.
- -galaktikum zu galaxis „Milchstraße“: Perigalaktikum und Apogalaktikum sind die Punkte auf der Umlaufbahn eines Sterns um das Zentrum des Milchstraßensystems, auf dem er am nächsten bzw. am weitesten von diesem entfernt ist.
- -jovum zu lat. iupiter: beim Jupiter sagt man Perijovum und Apojovum (englisch Peri-, Apojove, vom lateinischen Genitiv Iovis für des Jupiters).
- -ares zu griech. Ares: Beim Mars heißen die Apsiden Periares und Apares nach der griechischen Gottheit.
- Weitere Planeten: Für die anderen Planeten wären an Peri- bzw. Apo- konsequenterweise griechische Namen anzuhängen. Meistens werden sie umschrieben, analog beim Umlauf von Exoplaneten um ihren Zentralstern.
Weitere Begriffe
Perizentrum und Apozentrum (von griechisch kentron „Mittelpunkt“, wo man den Stachel des Zirkels ansetzt) bezeichnen dabei speziell Punkte in einem Mehrkörper-System und beziehen sich auf dessen Schwerpunkt, genauer gesagt das Baryzentrum. Ein Beispiel ist der Punkt auf der Umlaufbahn eines Partners in einem Doppelsternsystem, auf dem dieser am nächsten bzw. am weitesten vom Baryzentrum des Systems entfernt ist. Ist in einem allgemein himmelsmechanischen Zusammenhang von den Apsiden einer Bahn die Rede, ohne dass ein bestimmter Zentralkörper spezifiziert werden soll, dann können sie ebenfalls als Perizentrum und Apozentrum, aber auch als Perifokus und Apofokus (lateinisch focus „Brennpunkt“) bezeichnet werden.
Der Abstand zwischen System-Baryzentrum und Apside ist die Apsisdistanz (Apsidendistanz), oder Apsisabstand, also Periheldistanz (Perihelabstand, oft auch kurz nur „Perihel“), Apheldistanz (Aphelabstand, „Aphel“), Perizentrumsdistanz usw. Zu beachten ist, dass „Periapsisdistanz“ („Periapsisabstand“) manchmal auch als Bahnelement den Winkel Argument der Periapsis bezeichnet.
Die Verbindungslinie der beiden Apsiden ist die Apsidenlinie.
Grundlagen
Exzentrizität und Apsisdistanz
Der Zusammenhang zwischen (numerischer) Exzentrizität und den Apsisdistanzen ist
Apsiden und Apsidenlinie
Die Gerade durch die beiden Apsiden wird Apsidenlinie genannt. Die Verbindungsstrecke beider Punkte entspricht der Hauptachse der Ellipse. Für die Bahnberechnung wird häufig deren halbe Größe als „große Halbachse“ oder „mittlere Entfernung“ angegeben.
Bahnellipsen und Baryzentrum
Wenn man Bahndaten näher betrachtet und die zwei Apsidendistanzen mittelt, fällt manchmal auf, dass sich diese mittlere Entfernung von der großen Halbachse unterscheidet. Wenn der Zentralkörper nicht wesentlich größer als der zweite ist, wird daran der Effekt des Baryzentrums deutlich gemacht. Denn nicht der Mittelpunkt des Zentralkörpers steht im Brennpunkt der Bahnellipse, sondern das Baryzentrum als der gemeinsame Schwerpunkt der Himmelskörper.
Beim System Erde-Mond liegt das Baryzentrum (der Erde-Mond-Schwerpunkt) fast 5000 km außerhalb des Geozentrums, also im mondzugewandten Bereich des Erdmantels. Der Erdmittelpunkt beschreibt daher monatlich eine Ellipse von 10.000 km Durchmesser.
Bei Doppelsternen (siehe unten) ist dieser Effekt noch wesentlich größer und kann vielfach sogar astrometrisch erfasst werden. So wurde beispielsweise schon um 1800 eine periodische Ortsveränderung des hellen Sterns Sirius festgestellt, aber erst 1862 sein kleiner Begleiter optisch nachgewiesen -- als erster astrometrischer Doppelstern.
Bei dem Nachweis von Exoplaneten mit der Radialgeschwindigkeitsmethode wird dieser Effekt ausgenutzt, um aus dem radialen Bewegungsanteil des Muttersterns um das Baryzentrum auf Masse und Umlaufdauer der Planeten zu schließen.
Während des Durchgangs eines Körpers durch seine Periapsis besitzt er seine größte Bahngeschwindigkeit, weil er bis dorthin – aufgrund des abnehmenden Bahnradius – auf das Gravizentrum zufällt; während seines Durchgangs durch die Apoapsis seine geringste Umlaufgeschwindigkeit, weil er sich bis dorthin vom Gravizentrum entfernt. Die Winkelgeschwindigkeit (scheinbare Geschwindigkeit) im Umlaufzentrum ändert sich noch mehr, weil sich zusätzlich zu dem im gleichen Zeitabschnitt durcheilten Bogen auch die Distanz (der Radius) verkürzt – dieser Effekt ist etwa bei der Beobachtung der täglichen Bewegung des Mondes oder eines Satelliten auffallend.
Bahnstörungen
In Abwesenheit von Schwerkraftseinflüssen anderer Himmelskörper und unter Vernachlässigung relativistischer Effekte hätte eine Apsidenlinie stets dieselbe Ausrichtung im Raum. Da der umlaufende Körper in der Regel jedoch solchen Störungen ausgesetzt ist, bleibt die Apsidenlinie nicht fest, sondern dreht sich langsam in Richtung des umlaufenden Himmelskörpers. Dieser Vorgang wird Apsidendrehung genannt. Weist die Bahn eines Himmelskörpers eine merkliche Apsidendrehung auf, so muss zwischen seiner anomalistischen Umlaufperiode (Rückkehr zur selben Apsis) und seiner kleineren siderischen Umlaufperiode (Rückkehr zur selben Stellung bezüglich des Fixsternhintergrunds) unterschieden werden.
Die Störungen durch andere Himmelskörper können neben der Apsidendrehung auch geringfügige kurzzeitige Verformungen einer Umlaufbahn bewirken. Der größte und der kleinste Abstand dieser verformten Bahn vom Zentralkörper werden sich an etwas anderen Stellen befinden als die Apsiden der ungestörten Bahn. Dies beeinflusst sowohl die Zeitpunkte der Apsidendurchläufe als auch die betreffenden Apsisdistanzen.
System Sonne-Erde
Bei der Erde kreist nicht wie bei mondlosen Planeten ihr Mittelpunkt, sondern der mit ihrem Mond gemeinsame Schwerpunkt (Baryzentrum) auf einer Kepler-Ellipse um die Sonne. Dieser Schwerpunkt liegt zwar noch im Erdinneren – in ca. 1700 km Tiefe – doch im Mittel etwa 4670 km vom Erdmittelpunkt entfernt. Der Erdmittelpunkt vollführt folglich eine Schlangenlinie über der Ellipse.
| Periheldurchgang des Erde-Mond-Schwerpunkts | ||
|---|---|---|
| Jahr | Datum | Sonnenabstand (AE) |
| 2010 | 3. Januar 18h MEZ | 0,983314 |
| 2011 | 4. Januar 01h MEZ | 0,983310 |
| 2012 | 4. Januar 04h MEZ | 0,983303 |
| 2013 | 3. Januar 07h MEZ | 0,983306 |
| 2014 | 3. Januar 16h MEZ | 0,983311 |
| 2015 | 4. Januar 01h MEZ | 0,983309 |
| 2016 | 4. Januar 05h MEZ | 0,983296 |
| 2017 | 3. Januar 09h MEZ | 0,983297 |
| 2018 | 3. Januar 15h MEZ | 0,983312 |
| 2019 | 3. Januar 23h MEZ | 0,983273 |
| 2020 | 4. Januar 06h MEZ | 0,983253 |
Periheldurchgang des Erde-Mond-Schwerpunkts
Der Schwerpunkt durchläuft den Scheitelpunkt der Ellipse jeweils in mittleren Zeitabständen von einem anomalistischen Jahr, also 365 Tagen und gut sechs Stunden. Nach Ablauf eines Kalenderjahres von 365 Tagen braucht der Schwerpunkt daher noch weitere sechs Stunden, um den Scheitelpunkt wieder zu erreichen. Jeder Durchgang findet deshalb zu einer um etwa sechs Stunden späteren Uhrzeit statt, bis nach vier Jahren ein Schalttag den Durchgang wieder um einen Tag vorverlegt (man vergleiche ähnliche Muster beim Beginn der einzelnen Jahreszeiten). Da das Schaltjahrschema jedoch dafür ausgelegt ist, den Kalender mit dem tropischen Jahr und nicht mit dem um etwa 25 Minuten längeren anomalistischen Jahr zu synchronisieren, wandert der Zeitpunkt des Scheiteldurchgangs langfristig rückwärts durch den Kalender.
In der Tabelle[6] sind die auflaufende jährliche Verspätung und das Zurückspringen nach einem Schaltjahr (fett markiert) deutlich zu erkennen. Die verbleibenden Abweichungen von einer strengen Regelmäßigkeit sind auf die Gravitationseinflüsse der übrigen Planeten zurückzuführen, welche die Erdbahn geringfügig verformen, so dass die genaue Lage ihres sonnennächsten Punktes stets ein wenig hin und her wandert.
Größte Sonnennähe des Erdmittelpunkts
Der Erdmittelpunkt vollführt die bereits erwähnte Schlangenlinie über der vom Schwerpunkt Erde/Mond (Baryzentrum) verfolgten Keplerellipse. Der Zeitpunkt der größten Sonnennähe der Erde ist deshalb im Allgemeinen nicht derjenige, an dem das Baryzentrum den Ellipsenscheitel passiert. Er wird auch von der Mondphase bestimmt, die zur Perihel-Zeit besteht:[7]
- Bei zunehmendem Mond erreicht der Erdschwerpunkt später als das Baryzentrum seine größte Sonnennähe, bei abnehmendem Mond ist es umgekehrt. Der Zeitunterschied ist bei Halbmond am größten und kann bis etwa 32 Stunden betragen.
- Wenn sich der Mond bei der Scheitelpassage des Baryzentrums im ersten Viertel (zunehmender Mond) befindet, so bewegt sich die Erde gerade mit maximaler Geschwindigkeit in Richtung zur Sonne. Der Mond entfernt sich mit maximaler Geschwindigkeit, der Abstand der Erde von der Sonne nimmt immer noch ab, und die maximale Sonnennähe ist später als jene des Baryzentrums. Der Abstand des Baryzentrums von der Sonne wächst zwar nach dem Verlassen des Scheitels, aber die vom Mond verursachte Annäherung der Erde an die Sonne überwiegt mehr als einen Tag lang.
- Beim dritten Viertel (abnehmender Mond) hat sich die Erde mehr als einen Tag früher der Sonne am nächsten befunden und entfernt sich anschließend mit maximaler Geschwindigkeit von der Sonne weg (Mond mit maximaler Geschwindigkeit in Sonnen-Richtung). Wenn das Baryzentrum im Bahnscheitel ist, hat die Erde bereits eine positive Geschwindigkeit von der Sonne weg, und die maximale Sonnennähe war früher als jene des Baryzentrums.
Im Beispiel für 1989 (siehe auch Abbildung Bewegung der Erde auf Schlangenlinien um die Sonne) war der Mond am 30. Dezember 1988 im dritten Viertel. Die von ihm verursachte schnelle Wegbewegung der Erde von der Sonne wurde aber von der noch relativ schnellen Näherung des Baryzentrums an die Sonne bis zur Nacht vom 1. zum 2. Januar (etwa 27 Stunden vor dem am 3. Januar stattfindenden Scheiteldurchgang des Baryzentrums) überboten.
- Bei Vollmond und Neumond passieren Erdschwerpunkt, Baryzentrum und Mond ihre Ellipsenscheitel etwa gleichzeitig. Bei Vollmond ist die Sonnennähe der Erde absolut am größten und kann exakt im Scheitel stattfinden. Bei Neumond ist die größte Sonnennähe im gegenseitigen Vergleich aller Mondphasen am kleinsten und liegt immer kurz vor oder nach dem Scheitel.
In den Jahren 2010 bis 2020 wird die größte Sonnennähe maximal etwa 29 Stunden früher (2016) beziehungsweise maximal etwa 30 Stunden später (2017) als die Scheitelpassage des Baryzentrums erreicht, siehe unten stehende Tabelle. Die frühesten und spätesten kalendarischen Momente der größten Sonnennähe der Erde in den Jahren 1980 bis 2020 sind der 1. Januar 1989 23h MEZ (etwa 27½ Stunden vor der Scheitelpassage des Baryzentrums, abnehmender Mond, Schalttag vorhergehend, 29. Februar 1988) und der 5. Januar 2020 9h MEZ (etwa 27 Stunden nach der Scheitelpassage des Baryzentrums, zunehmender Mond, Schalttag folgend, 29. Februar 2020).[8][9][6] Man beachte, dass bei der Auswahl nach Kalenderdatum wegen des Schaltperiode-„Pendelns“ des Kalenders keine Aussage über die größten zeitlichen Abstände vom Moment der Scheitelpassage durch das Baryzentrum möglich ist, vgl. Werte 1989 gegen 2016 und 2020 gegen 2017.
Wegen der langsamen Drift des Perihels (Drehung der Apsidenlinie) werden sich diese Zeitpunkte auf spätere Kalenderdaten verschieben. Um das Jahr 1600 war größte Sonnennähe zwischen 26. und 28. Dezember. Um das Jahr 2500 herum wird sie auf den 10. bis 13. Januar fallen.[8][10]
Die für die Sonnennähe beschriebenen Verhältnisse gelten entsprechend auch für die Sonnenferne. Die folgende Tabelle listet Zeitpunkte für beide Fälle auf.[9]
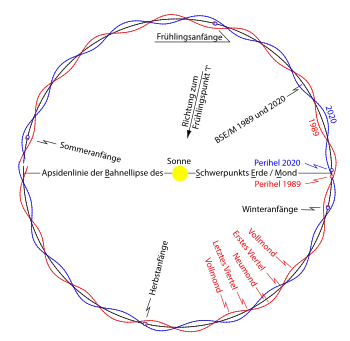
Schwarze Grundlinie: Elliptische Bahn des Schwerpunkts Erde/Mond.
Schlangenlinien: Erdbahnen rot (größte Sonnennähe/„Perihel 1989“ am 1. Januar bei abnehmendem Mond) und blau (größte Sonnennähe/„Perihel 2020“ am 5. Januar bei zunehmendem Mond) mit 1000-fach überhöht dargestelltem Mondeinfluss.[11]
| größte Sonnennähe der Erde | größte Sonnenferne der Erde | |||||
|---|---|---|---|---|---|---|
| Jahr | Datum (MEZ) | ± | Sonnenabstand (AE) | Datum (MEZ) | Sonnenabstand (AE) | |
| 2010 | 3. Januar 01h | −17 | 0,98329 | 6. Juli 14h | 1,01670 | |
| 2011 | 3. Januar 20h | −5 | 0,98334 | 4. Juli 17h | 1,01674 | |
| 2012 | 5. Januar 02h | +22 | 0,98328 | 5. Juli 06h | 1,01668 | |
| 2013 | 2. Januar 06h | −25 | 0,98329 | 5. Juli 17h | 1,01671 | |
| 2014 | 4. Januar 13h | +21 | 0,98333 | 4. Juli 02h | 1,01668 | |
| 2015 | 4. Januar 08h | +7 | 0,98328 | 6. Juli 22h | 1,01668 | |
| 2016 | 2. Januar 24h | −29 | 0,98330 | 4. Juli 18h | 1,01675 | |
| 2017 | 4. Januar 15h | +30 | 0,98331 | 3. Juli 22h | 1,01668 | |
| 2018 | 3. Januar 07h | −8 | 0,98328 | 6. Juli 19h | 1,01670 | |
| 2019 | 3. Januar 06h | −17 | 0,98330 | 4. Juli 24h | 1,01675 | |
| 2020 | 5. Januar 09h | +27 | 0,98324 | 4. Juli 14h | 1,01669 | |
Spalte ± : nach (+) bzw. vor (-) der Scheitelpassage des Baryzentrums in Stunden
Siehe auch
Einzelnachweise
- Apside (1.), in: Duden online
- Wilhelm Pape, Max Sengebusch (Bearb.): Handwörterbuch der griechischen Sprache. 3. Auflage, 6. Abdruck. Vieweg & Sohn, Braunschweig 1914, S. 421 (Digitalisat [abgerufen am 13. August 2018]).
- Wilhelm Pape, Max Sengebusch (Bearb.): Handwörterbuch der griechischen Sprache. 3. Auflage, 6. Abdruck. Vieweg & Sohn, Braunschweig 1914, S. 294 (Digitalisat [abgerufen am 13. August 2018]).
- Wilhelm Pape, Max Sengebusch (Bearb.): Handwörterbuch der griechischen Sprache. 3. Auflage, 6. Abdruck. Vieweg & Sohn, Braunschweig 1914, S. 564 (Digitalisat [abgerufen am 13. August 2018]).
- http://solarsystem.nasa.gov/planets/compare (Link nicht abrufbar)
- Aus dem Ephemeridenserver HORIZONS Web-Interface des JPL ausgelesen. Observer Location: „Sun (body center)“, Target Body: „Earth-Moon Barycenter [EMB]“, Ausgabe von Zielentfernung „Obsrv range“ und Lichtlaufzeit „One-Way Light-Time“. Minimale Entfernung durch quadratische Interpolation auf 10-Minuten-Raster ermittelt; zugehörigen Zeitpunkt um Lichtlaufzeit korrigiert.
- Siegfried Wetzel: Das Perihel der Erde
- J. Meeus: Mathematical Astronomy Morsels. Willmann-Bell. Richmond 1997. ISBN 0-943396-51-4. Kap. 27
- Aus dem Ephemeridenserver HORIZONS Web-Interface des JPL ausgelesen. Observer Location: „Sun (body center)“, Target Body: „Earth [Geocenter]“, Ausgabe von Zielentfernung „Obsrv range“ und Lichtlaufzeit „One-Way Light-Time“. Minimale Entfernung durch quadratische Interpolation auf 10-Minuten-Raster ermittelt; zugehörigen Zeitpunkt um Lichtlaufzeit korrigiert. Zeitpunkte durch Vergleich mit Earth's Seasons – Equinoxes, Solstices, Perihelion, and Aphelion, 2000–2020 (Memento vom 8. Oktober 2015 im Internet Archive) kontrolliert.
- Earth at Perihelion and Aphelion: 1501 to 1600 ... Earth at Perihelion and Aphelion: 2001 to 2100 ... Earth at Perihelion and Aphelion: 2401 to 2500 von Fred Espenak (astropixels.com), abgerufen 8. Juli 2021
- MICA 2.0: „Multiyear Interactive Computer Almanac 1800–2050“, U.S. Naval Observatory, Washington, 2005, publ. by Willmann-Bell, Inc.