Bahnresonanz
In der Himmelsmechanik liegt eine Bahnresonanz (oder kurz Resonanz) vor, wenn zwei oder mehrere Himmelskörper periodisch wiederkehrenden gravitativen Einflüssen unterliegen. Ursachen von Bahnresonanzen sind die Umlaufzeiten der beteiligten Himmelskörper, deren Verhältnis zueinander durch niedrige natürliche Zahlen beschrieben werden kann, beispielsweise durch 2:1 oder 3:2.
Zwischen den Umlaufzeiten einiger unserer Planeten herrschen harmonikale Verhältnisse, beschrieben von Johannes Kepler in seiner „Harmonice mundi“.
Auswirkungen
Resonanzen können sowohl eine störende als auch eine stabilisierende Wirkung auf die Bahnen der Himmelskörper haben. Dies ist abhängig von der geometrischen Konstellation der beteiligten Himmelskörper. Bahnveränderungen durch periodische Störungen (siehe Resonanz), die stets an derselben Bahnposition ausgeübt werden, summieren sich im Falle einer instabilen, störenden Resonanz oder kompensieren sich gegenseitig im Fall einer stabilen Resonanz.
Störende Resonanzen
Im Falle störender Resonanzen führen die periodisch wiederkehrenden Störungen über längere Zeiträume zu dramatischen Änderungen der Bahnform. Häufigstes Resultat ist das Anwachsen der Exzentrizität, bis der Himmelskörper auf Kollisionskurs mit einem anderen Objekt gerät oder bei einer nahen Passage aus dem System herausgeschleudert wird.
Beispiele für störende Resonanzen sind die durch die Saturnmonde bedingten Teilungen der Saturnringe und die Kirkwoodlücken im Asteroidengürtel. Letzterer gilt als der wahrscheinlichste Herkunftsort der erdnahen Asteroiden.
Stabilisierende Resonanzen
Bei stabilisierenden Resonanzen verteilen sich die Orte der Bahnstörungen regelmäßig auf der Bahn des gestörten Objekts, sodass sich ihre Wirkungen gegeneinander aufheben.
Beispiele
- Der Zwergplanet Pluto und zahlreiche kleinere Objekte im Kuipergürtel, die als Plutinos bezeichnet werden, befinden sich in einer 3:2-Resonanz mit Neptun, d. h. während dreier Neptunumläufe umrunden sie die Sonne zweimal. Weiter außerhalb befinden sich weitere resonante Kuipergürtelobjekte, die in 2:1-Resonanz zur Neptunbahn stehen. Es existieren auch Objekte mit anderen Resonanzen, wie zum Beispiel mit 5:2, 3:1 und 4:1 (siehe unten).
- Eine Sonderform der Bahnresonanz mit dem Verhältnis 1:1 bilden die koorbitalen Objekte. Das bekannteste Beispiel dafür sind die so genannten Trojaner. Sie befinden sich in einem der Lagrange-Punkte L4 oder L5 bezüglich der Sonne und eines Planeten (meistens Jupiter).
- Eine Vielzahl kleinerer Asteroidengruppen außerhalb des Hauptgürtels zwischen Mars und Jupiter werden durch Resonanzen zur Jupiterbahn stabilisiert, darunter die Hilda-Gruppe bei 3:2 und die Cybele-Gruppe bei 7:4.
- Im extrasolaren Planetensystem um den Stern Ypsilon Andromedae A befindet sich der zweitinnerste Planet Ypsilon Andromedae d in einer 3:1-Resonanz mit dem äußersten Planeten Ypsilon Andromedae e.[1]
Kuipergürtel: Umlaufbahn-Resonanzen zum äußersten Gasplaneten Neptun
Eine besonders stabile Umlaufbahn liegt dann vor, wenn sich die Kleinplaneten des Kuipergürtels mit Neptun in einer 3:2 Umlaufbahnresonanz befinden; das bedeutet, dass sie zweimal die Sonne umkreisen, während Neptun drei Umläufe macht. Da auch Pluto eine solche Umlaufbahn hat, nennt man solche Kuipergürtel-Objekte „Plutinos“, die mit Orcus noch einen zweiten mutmaßlichen Zwergplaneten und dazu mehrere Zwergplaneten-Kandidaten enthalten.
Es gibt auch andere Umlaufbahnresonanzen, die ebenfalls für stabile Bahnen sorgen, beispielsweise die 5:2 Umlaufbahnresonanz, die 3:1 Umlaufbahnresonanz und die 4:1 Umlaufbahnresonanz.
Mit Ausnahme der Kuipergürtel-Objekte 2004 XR190 „Buffy“ und (523635) 2010 DN93 haben alle Kuipergürtel-Objekte mit mehr als eineinhalbfachem Neptunabstand und moderat-elliptischen Umlaufbahnen eine stabile 5:2-, 3:1- oder 4:1-Umlaufbahnresonanz zu Neptun. Nach dem 3. Keplerschen Gesetz kann man diese Umlaufbahnresonanzen einfach herausfinden, denn sie hängen nur von der Großen Halbachse der Umlaufbahnen ab, insbesondere nicht von ihrem Perihel. Somit kann ein Planetoid dadurch in eine solche stabile Bahn gelangen, indem seine Umlaufbahn etwas mehr oder etwas weniger elliptisch verläuft.
Beispiele für 5:2-resonante Objekte mit hohen Perihelen: 2015 KQ174
Beispiele für 3:1-resonante Objekte mit hohen Perihelen: 2015 FJ345, 2014 JM80, 2013 FQ28, 2013 SK100
Beispiele für 4:1-resonante Objekte mit hohen Perihelen: 2014 FZ71, 2014 FC72, (145480) 2005 TB190
Man kann zeigen,[2] dass wenn solche Planetoiden eine mittelhohe Bahnneigung ab etwa 40 Grad Bahnneigungswinkel haben, ihre Umlaufbahnen auch bei nicht ganz so schönen Bahnresonanzen stabil sind. Sowohl „Buffy“ als auch der Zwergplaneten-Kandidat 2010 DN93 haben ungefähr eine 8:3-Umlaufbahnresonanz zu Neptun und eine genügend hohe Bahnneigung, dass auch ihre Umlaufbahnen stabil sind.
Die Umlaufbahnen dieser Kuipergürtel-Objekte, die hohe Perihele bis über 55 AU aufweisen, sind somit gut verstanden und stabil.
Weitere Typen
Säkulare Resonanz
Eine säkulare Resonanz liegt vor, wenn die Bewegung des Perihels oder die des Knotens zweier oder mehrerer Himmelskörper miteinander synchronisiert ist. Die Präzessionsfrequenz kleinerer Körper passt sich in diesem Fall der des störenden massereichen Körpers an.
Kozai-Mechanismus
Beim Kozai-Mechanismus handelt es sich um eine periodische und synchrone Änderung der Exzentrizität und Bahnneigung eines Himmelskörpers infolge von Resonanzeffekten.
Laplace-Resonanz
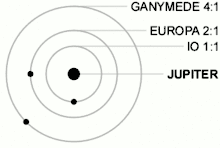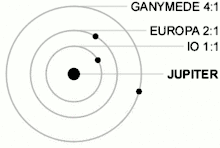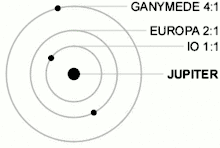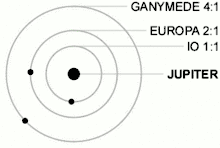
Bei einer Laplace-Resonanz stehen die Umlaufzeiten dreier oder mehrerer Himmelskörper in einem niedrigen ganzzahligen Verhältnis zueinander. Im Sonnensystem stehen Umlauffrequenzen der drei inneren Galileischen Monde des Jupiter (Io, Europa, Ganymed) in einer Resonanz von 4:2:1 – vier Io-Umläufe auf zwei Europa-Umläufe und einen Ganymed-Umlauf. Die drei äußeren Planeten von Gliese 876 (Gliese 876 c, Gliese 876 b, Gliese 876 e) stehen ebenfalls in 4:2:1-Resonanz: Vier Umläufe von Gliese 876 c entfallen auf zwei von Gliese 876 b und einen von Gliese 876 e. Fünf der sechs bekannten Planeten (Stand 2021) von TOI-178 stehen in einer 2:4:6:9:12-Kette von Laplaceresonanzen.[3][4][5]
Siehe auch
Literatur
- Joachim Krautter et al.: Meyers Handbuch Weltall. 7. Auflage. Meyers Lexikonverlag, 1994, ISBN 3-411-07757-3, S. 144
Einzelnachweise
- Curiel et al. A fourth planet orbiting υ Andromedae. In: Astronomy & Astrophysics, Ausgabe 525, 2011
- Scott S. Sheppard, Chadwick Trujillo, David J. Tholen: Beyond the Kuiper Belt Edge: New High Perihelion Trans-Neptunian Objects With Moderate Semi-major Axes and Eccentricities. In: The Astrophysical Journal Letters. Nr. 825(1), 2015, arxiv:1606.02294.
- Puzzling six-exoplanet system with rhythmic movement challenges theories of how planets form. In: ESO, 25. Januar 2021.
- ESA's exoplanet watcher Cheops reveals unique planetary system. In: ESA, 25. Januar 2021.
- A. Leleu, Y. Alibert, N. C. Hara, M. J. Hooton, T. G. Wilson, P. Robutel, J.-B. Delisle, J. Laskar, S. Hoyer, C. Lovis, E. M. Bryant, E. Ducrot, J. Cabrera, J. Acton, V. Adibekyan, R. Allart, C. Allende Prieto, R. Alonso, D. Alves, D. R. Anderson: Six transiting planets and a chain of Laplace resonances in TOI-178. In: Astronomy & Astrophysics. 20. Januar 2021, ISSN 0004-6361. arxiv:2101.09260. doi:10.1051/0004-6361/202039767.