Winkelhalbierende

In der ebenen Geometrie ist die Winkelhalbierende eines Winkels die Halbgerade, die durch den Scheitelpunkt des Winkels läuft und das Winkelfeld in zwei deckungsgleiche Teile teilt.

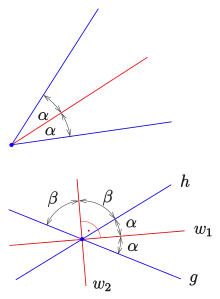
Winkelhalbierende eines Winkels bzw. zweier Geraden

Ein schneidendes Geradenpaar bestimmt zwei Winkelhalbierende, in diesem Falle Geraden, die zueinander orthogonal sind. Jede dieser Winkelhalbierenden ist eine Symmetrieachse der geometrischen Figur, die von dem schneidenden Geradenpaar gebildet wird. Aus dieser Symmetrieeigenschaft folgt eine Charakterisierung der beiden Winkelhalbierenden als geometrischer Ort, die als Winkelhalbierendensatz bezeichnet wird.

In der analytischen Geometrie und in der Analysis spielen die Winkelhalbierenden der Koordinatenachsen eines kartesischen Koordinatensystems eine besondere Rolle. Diejenige, die durch den I. und III. Quadranten verläuft, heißt 1. Winkelhalbierende oder 1. Mediane, die andere 2. Winkelhalbierende.

In der synthetischen Geometrie werden die Winkelhalbierenden eines schneidenden Geradenpaars ebenfalls durch ihre Eigenschaft als Symmetrieachsen definiert. Die Existenz dieser Winkelhalbierenden ist dort eines der Axiome, die eine frei bewegliche präeuklidische Ebene kennzeichnen.

Winkelhalbierende in der ebenen Geometrie

Konstruktion

Ein Winkel ist durch seine beiden Schenkel, also die Halbgeraden mit gemeinsamen Anfang im Scheitel des Winkels, gegeben. Dann kann die Winkelhalbierende mit Zirkel und Lineal konstruiert werden: Um den Scheitelpunkt wird ein Kreis mit beliebigem Radius gezeichnet. An den Schnittpunkten mit den Schenkeln des Winkels wird der Zirkel erneut angesetzt. Dann zeichnet man jeweils einen Kreis mit gleichem Radius. Die Schnittpunkte dieser zwei Kreise liegen auf der Winkelhalbierenden.

Bei dieser Konstruktion wird benutzt, dass die Winkelhalbierende zugleich Mittelsenkrechte in dem gleichschenkligen Dreieck ist, das durch den Scheitel und die zwei ersten Hilfspunkte gegeben ist.

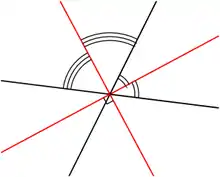
Die Winkelhalbierenden (rot) zweier Geraden sind zueinander orthogonal.

Konstruktion einer Winkelhalbierenden mit Zirkel und Lineal. Dazu müssen drei Kreise oder Kreisbögen gezeichnet werden.

Liegen allgemeiner zwei Geraden vor, die sich in einem Punkt schneiden, so haben wir vier Winkel und damit vier Winkelhalbierende. Die Winkelhalbierenden zweier Scheitelwinkel fallen zusammen, also bleiben nur zwei Winkelhalbierende übrig. Diese zwei Winkelhalbierenden – die zueinander orthogonal sind – nennt man die Winkelhalbierenden der zwei Geraden (siehe Abbildung rechts).

Wenn wir wieder zu dem Fall eines Winkels zurückkommen, der von zwei Schenkeln (Halbgeraden) begrenzt wird, und nun diese Schenkel zu Geraden verlängern, dann bekommen wir zwei Geraden mit zwei Winkelhalbierenden. Die eine ist die Winkelhalbierende des ursprünglichen Winkels. Die andere ist die Winkelhalbierende seines Nebenwinkels. Sie heißt Außenwinkelhalbierende des ursprünglichen Winkels.

Winkelhalbierendensatz

Die Vereinigungsmenge der beiden Winkelhalbierenden eines schneidenden Geradenpaars ist die Menge aller Punkte, die von den beiden Geraden den gleichen Abstand haben, oder, anders formuliert, die Menge der Mittelpunkte aller Kreise, die die beiden Geraden berühren.

Winkelhalbierende im Dreieck

Die 3 Außenwinkelhablierenden:
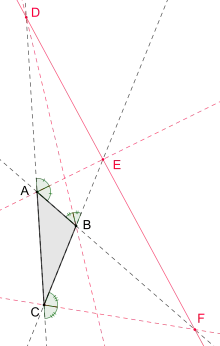
Die 3 Schnittpunkte D, E, F liegen auf einer Geraden (rot) und es gelten die folgenden Streckenverhältnisse:

{\begin{aligned}{\frac {|EB|}{|EC|}}&={\frac {|AB|}{|AC|}}\\{\frac {|FB|}{|FA|}}&={\frac {|CB|}{|CA|}}\\{\frac {|DA|}{|DC|}}&={\frac {|BA|}{|BC|}}\end{aligned}}

Ist in der Dreieckslehre von Winkelhalbierenden die Rede, so bezieht sich dieser Begriff meist auf die Innenwinkel, seltener auf die Außenwinkel. Hier wird die Winkelhalbierende eines Innenwinkels $\alpha$ oft als $w_{\alpha }$ abgekürzt. Dieses Kürzel steht dann zugleich auch für die Strecke auf der Winkelhalbierenden, die innerhalb des Dreiecks liegt, und in Konstruktionsaufgaben auch für deren Länge.

Für diese Winkelhalbierenden gelten unter anderem folgende Sätze:

Die drei Winkelhalbierenden der Innenwinkel eines Dreiecks schneiden sich in einem Punkt. Dieser Punkt ist der Mittelpunkt des Inkreises (siehe Ausgezeichnete Punkte im Dreieck).
Jede Winkelhalbierende eines Innenwinkels im Dreieck teilt die gegenüberliegende Seite im Verhältnis der anliegenden Seiten. Diese Aussage wird auch als Winkelhalbierendensatz bezeichnet und lässt sich mithilfe ähnlicher Dreiecke oder durch Anwendung des Sinussatzes beweisen.
Für die Länge $w$ der Halbierenden eines Innenwinkels $\gamma$ und für die anliegenden Seiten der Länge $a$ und $b$ gilt die Beziehung
${\frac {2\cos {\frac {\gamma }{2}}}{w}}={\frac {1}{a}}+{\frac {1}{b}}$ .
Die Halbierenden eines Innenwinkels und der zu den beiden anderen Innenwinkeln gehörenden Außenwinkel eines Dreiecks schneiden sich jeweils in einem Punkt. Dieser Punkt ist der Mittelpunkt eines Ankreises.
Die Schnittpunkte der Halbierenden der Außenwinkel mit den verlängerten Gegenseiten der entsprechenden Innenwinkel liegen, sofern sie existieren, auf einer Geraden.

Winkelhalbierende im Viereck

Die Winkelhalbierenden eines Vierecks begrenzen im Allgemeinen ein Sehnenviereck. Beim Tangentenviereck ist es zu einem Punkt entartet. Beim Sehnenviereck ist das eingeschlossene Viereck orthodiagonal. Die Winkelhalbierenden eines Parallelogramms schließen im Allgemeinen ein Rechteck ein, die Winkelhalbierenden eines Rechtecks ein Quadrat, die Winkelhalbierende eines gleichschenkligen Trapezes ein Drachenviereck, die Winkelhalbierende eines Vierecks mit gleichen gegenüberliegenden Winkeln ein gleichschenkliges Trapez.

Gleichungen

Sind die Gleichungen $a_{1}x+b_{1}y+c_{1}=0,\ a_{2}x+b_{2}y+c_{2}=0$ zweier Geraden gegeben, so ergeben sich die Gleichungen ihrer Winkelhalbierenden mit Hilfe ihrer Hesseschen Normalformen:

{\frac {a_{1}x+b_{1}y+c_{1}}{\sqrt {a_{1}^{2}+b_{1}^{2}}}}=\pm {\frac {a_{2}x+b_{2}y+c_{2}}{\sqrt {a_{2}^{2}+b_{2}^{2}}}}.

Denn die Winkelhalbierenden bilden die Gesamtheit der Punkte, die von den beiden Geraden den gleichen Abstand besitzen.

Winkelhalbierende eines Koordinatensystems

In einem kartesischen Koordinatensystem spielen die beiden Winkelhalbierenden der Koordinatenachsen eine besondere Rolle:

Als 1. Winkelhalbierende (Winkelhalbierende des I. und III. Quadranten) bezeichnet man die Gerade mit der Gleichung $y=x$ . Dieser Funktionsgraph ist die Ursprungsgerade mit der Steigung 1. Sie heißt in Österreich 1. Mediane.

Als 2. Winkelhalbierende (Winkelhalbierende des II. und IV. Quadranten) bezeichnet man die Gerade mit der Gleichung $y=-x$ . Dieser Funktionsgraph ist die Ursprungsgerade mit der Steigung −1.

Verallgemeinerungen

Mithilfe von iterativer Winkelhalbierung kann ein Winkel auch in $2\cdot 2=2^{2}=4$ , $2\cdot 2\cdot 2=2^{3}=8$ , $2\cdot 2\cdot 2\cdot 2=2^{4}=16$ oder allgemein in $2^{k}$ deckungsgleiche Teile geteilt werden. Dazu werden die halbierten Winkel jeweils erneut halbiert. Um einen Winkel zum Beispiel in $2\cdot 2\cdot 2\cdot 2=2^{4}=16$ gleiche Teile zu teilen, müssen nacheinander 4 Winkelhalbierende konstruiert werden.

Dieses Verfahren lässt sich verallgemeinern: Ist ein Winkel $\alpha$ gegeben, dann kann der Winkel ${\frac {n}{2^{k}}}\cdot \alpha$ konstruiert werden, wenn $n$ und $k$ natürliche Zahlen sind. Dabei hilft die Zahldarstellung im Binärsystem, denn der Quotient ${\frac {n}{2^{k}}}$ hat eine endliche Darstellung mit höchstens $k$ binären Nachkommastellen. Soll zum Beispiel der Winkel ${\frac {5}{8}}\cdot \alpha$ konstruiert werden, dann hilft die binäre Darstellung ${\frac {5}{8}}=[0{,}101]_{2}$ . Daraus ergibt sich ${\frac {5}{8}}\cdot \alpha =\alpha \cdot \left({\frac {1}{2}}+\left({\frac {1}{4}}-{\frac {1}{8}}\right)\right)={\frac {\alpha }{2}}+{\frac {\alpha }{4}}-{\frac {\alpha }{8}}$ . Der Winkel ${\frac {5}{8}}\cdot \alpha$ kann also konstruiert werden, indem am Scheitelpunkt nacheinander der Winkel ${\frac {\alpha }{2}}$ im Uhrzeigersinn, der Winkel ${\frac {\alpha }{4}}$ im Uhrzeigersinn und der Winkel ${\frac {\alpha }{8}}$ gegen den Uhrzeigersinn konstruiert wird.

Es gilt folgender Satz: Ist ein Winkel $\alpha$ gegeben und sind $p$ und $q$ natürliche Zahlen, dann kann der Winkel ${\frac {p}{q}}\cdot \alpha$ genau dann mit Zirkel und Lineal konstruiert werden, wenn $q$ eine Zweierpotenz ist, also $q=2^{k}$ . Für alle anderen natürlichen Zahlen $q$ ist das nicht möglich.[1]

Das geometrische Problem der Dreiteilung des Winkels, das seit dem 5. Jahrhundert v. Chr. bekannt ist, kann daher nicht mit Zirkel und Lineal gelöst werden.

Synthetische Geometrie

Eine präeuklidische Ebene ist in der synthetischen Geometrie eine affine Ebene $K^{2}$ über einem Körper $K$ , dessen Charakteristik nicht 2 ist, zusammen mit einer Orthogonalitätsrelation ohne isotrope Geraden $\perp$ zwischen den Geraden der Ebene. In einer solchen Ebene können (senkrechte) Achsenspiegelungen definiert werden (siehe Spiegelung (Geometrie) – Achsenspiegelung).

Als Winkelhalbierenden-Axiom wird die folgende Aussage bezeichnet:

Zu zwei Geraden $a,b$ existiert eine Gerade $w$ , so dass bei der Achsenspiegelung an $w$ die Gerade $a$ auf die Gerade $b$ abgebildet wird.

Sind die Geraden $a,b$ parallel und verschieden, so ist deren Mittelparallele eine Gerade, die die geforderte Symmetrieeigenschaft hat. Da Mittelparallelen in einer präeuklidischen Ebene immer existieren, ist die wesentliche Forderung die nach einer Symmetrieachse für ein schneidendes Geradenpaar, also nach einer Winkelhalbierenden. Aus der Existenz einer Winkelhalbierenden folgt stets die Existenz genau einer zweiten, die senkrecht zur ersten ist.

Eine präeuklidische Ebene, die das Axiom für Winkelhalbierende erfüllt, wird als frei bewegliche Ebene bezeichnet.

Literatur

Friedrich Bachmann: Aufbau der Geometrie aus dem Spiegelungsbegriff. 2. Auflage, Berlin; Göttingen; Heidelberg 1973

Zusammenfassung: Zur Begründung der Geometrie aus dem Spiegelungsbegriff. Mathematische Annalen, Bd. 123, 1951, S. 341ff

Wendelin Degen und Lothar Profke: Grundlagen der affinen und euklidischen Geometrie, Teubner, Stuttgart, 1976, ISBN 3-519-02751-8

Weblinks

Commons: Winkelhalbierende – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Winkelhalbierende – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wiktionary: Winkelsymmetrale – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Klassische Transversalen – Innen- und Außenwinkelhalbierende unter D.7

Einzelnachweise

Stephen Buckley, Desmond MacHale, Department of Mathematics, University College, Cork: Dividing an angle into equal parts

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Stephen Buckley, Desmond MacHale, Department of Mathematics, University College, Cork: Dividing an angle into equal parts